新井式回転抽選器が256角形だったときの当たり判定の最適化

前回と今回

前回の

https://zenn.dev/megeton/articles/17a434f9fc8e1d

は8角形だった。今回これを256角形としたときの計算量について考える。

問題点

8角形の場合は8個の辺と当たり判定を行っていた。それに比例して256角形の場合は256回の判定が必要になる。具体的にはボールは50個あるので 50個 * 8辺 = 400回 で済んだのが 50個 * 256辺 = 12800回 にもなる。

最適化

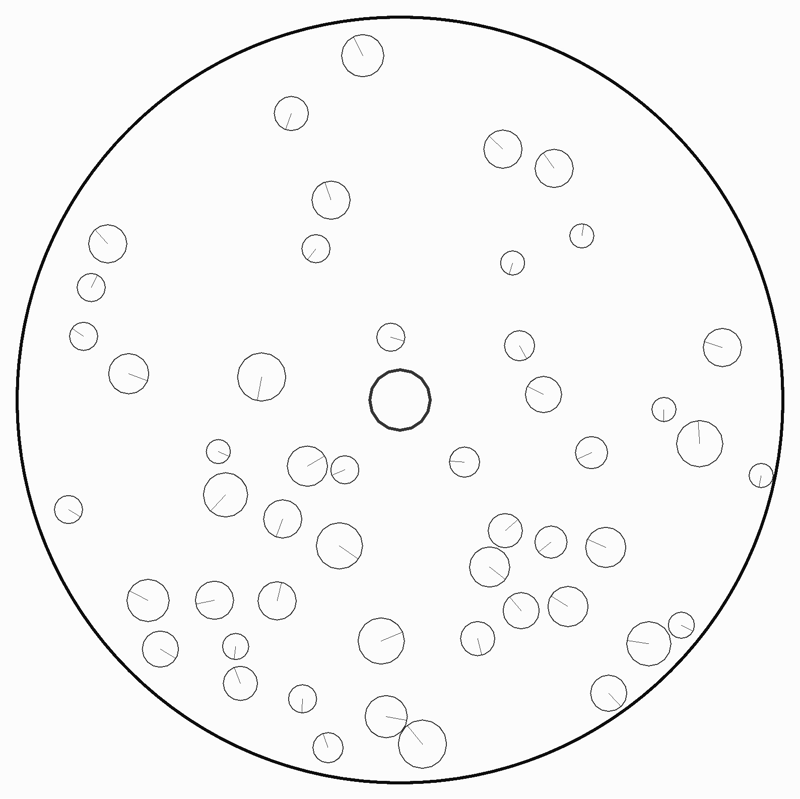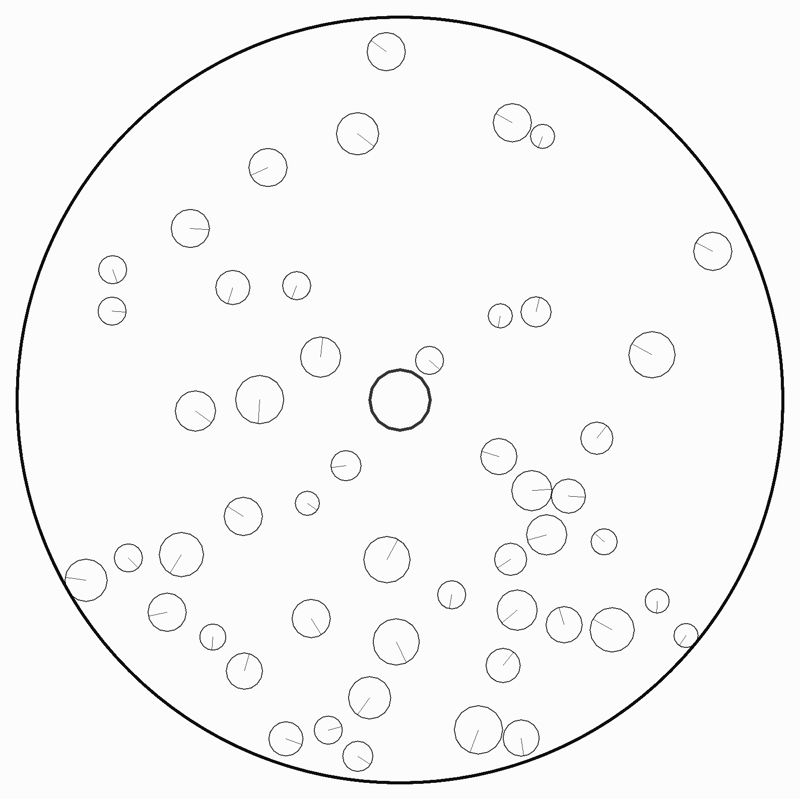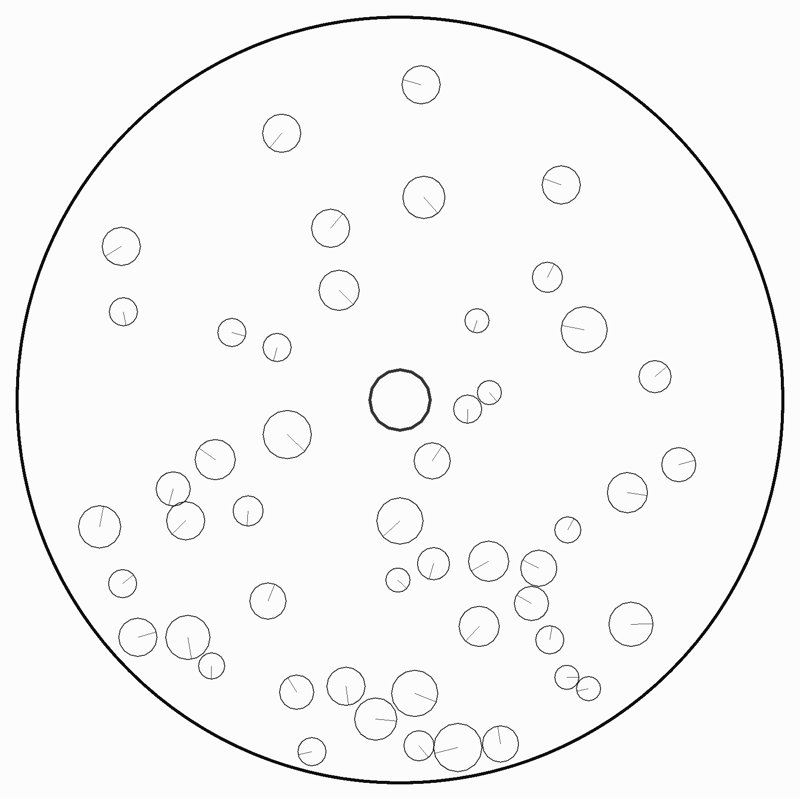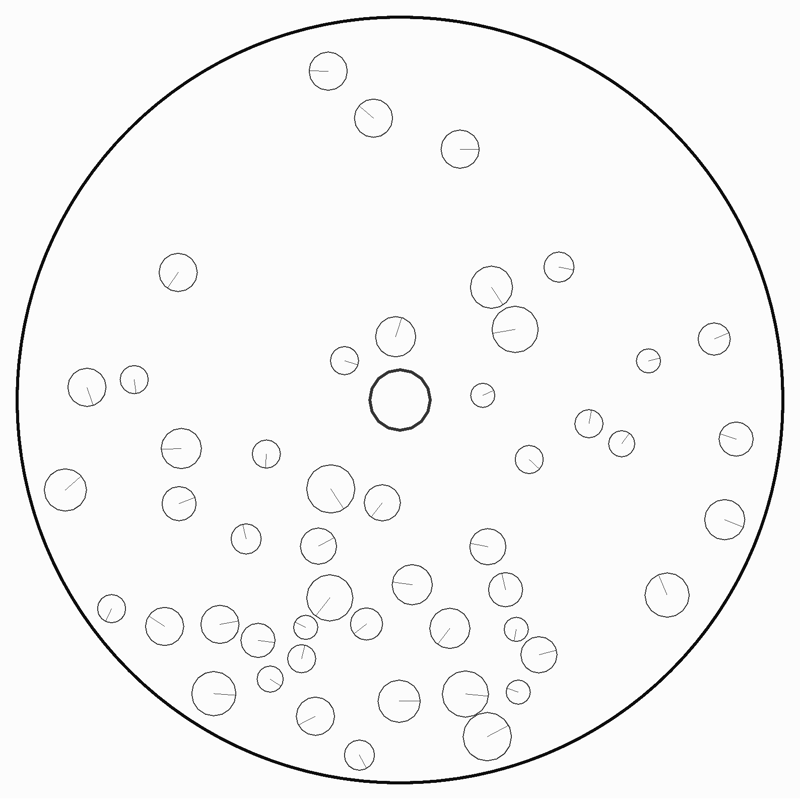
256角形

これは256角形というより円なので中心からの距離が半径を超えているかどうかで判定を行う。ただそれだけだが、これで O(ボール数 * N角形) は O(ボール数) で済むようになる。

8角形のときとのコードの違い

-  a = wall.p0
-  b = wall.p1
-  ab = b - a
-  ac = ball.location - a
-  n = ab.normalize.perp
-  distance = ac.dot(n)
+  ac = body.location - ball.location
+  n = ac.normalize
+  distance = body.radius - ac.length
t = distance / ball.radius
if t < 1.0
  ball.location = ball.location + n * (1.0 - t) * ball.radius
  ball.velocity = ball.velocity - ball.velocity.project_onto_normalized(n) * (1 + ball.restitution)
end

distance と n の求め方が変わっただけ。当たり判定は t を見ればわかるようにし、壁からの法線の正規化を n とすれば、判定・補正・反射のコードは共通化できる。

コード

class Ball
  attr_accessor :location
  attr_accessor :velocity
  attr_accessor :radius
  attr_accessor :mass

  def initialize
    @location = $app.window_wh.center + V.rand_norm
    @velocity = V.rand_norm
    @acceleration = V.zero
    @gravity = V[0.0, 0.008]
    @radius = rand(12..24)
    @mass = @radius**2
    @restitution = 0.999
  end

  def update
    $app.rebound(self, $app.pivot)

    ac = $app.body.location - @location
    n = ac.normalize
    distance = $app.body.radius - ac.length
    t = distance / @radius
    if t < 1.0
      @location = @location + n * (1.0 - t) * @radius
      @velocity = @velocity - @velocity.project_onto_normalized(n) * (1 + @restitution)
    end

    acceleration_add(@gravity * @mass)

    @velocity += @acceleration
    @location += @velocity
    @acceleration = V.zero
  end

  def draw
    $app.circle_draw(@location, @radius, sides: 16)
    $app.line_draw(@location, @location + @velocity.clamp_length_min(@radius))
  end

  def acceleration_add(force)
    @acceleration += force / @mass
  end
end

class Pivot
  attr_accessor :location
  attr_accessor :velocity
  attr_accessor :radius
  attr_accessor :mass

  def initialize
    @location = $app.window_wh.center
    @velocity = V.zero
    @mass = 1000000000.0
    @radius = 30.0
  end

  def update
    @location += velocity
  end

  def draw
    $app.circle_draw(location, radius, sides: 16, line_width: 3)
    $app.circle_draw(location, $app.body.radius, sides: 256, line_width: 3)
  end
end

class Body
  attr_accessor :location
  attr_accessor :radius

  def initialize
    @location = $app.window_wh.center
    @radius = $app.window_wh.center.min_element * 0.95
  end

  def draw
    $app.circle_draw(location, @radius, sides: 128, line_width: 3)
  end
end

class App < Base
  attr_accessor :body
  attr_accessor :pivot
  attr_accessor :balls

  def initialize
    super

    reset
  end

  def reset
    @body = Body.new
    @pivot = Pivot.new
    @balls = 50.times.collect { Ball.new }
  end

  def button_down(id)
    super

    case id
    when Gosu::KB_R
      reset
    end
  end

  def draw
    super

    @pivot.update
    @balls.combination(2) { |a, b| rebound(a, b) }
    @balls.each(&:update)

    @pivot.draw
    @body.draw
    @balls.each(&:draw)
  end

  def rebound(a, b)
    ab = b.location - a.location
    distance = ab.length
    gap = distance - a.radius - b.radius
    if gap.round.negative?
      len = -gap
      n = ab.normalize

      am = a.mass
      bm = b.mass

      a.location = a.location + n * len * -bm / (am + bm)
      b.location = b.location + n * len *  am / (am + bm)

      as = a.velocity.dot(n)
      bs = b.velocity.dot(n)

      e = 1.0
      as2 = (am*as + bm*bs - (e * bm * (as - bs))) / (am + bm)
      bs2 = (am*as + bm*bs + (e * am * (as - bs))) / (am + bm)

      a.velocity = a.velocity.reject_from_normalized(n) + n * as2
      b.velocity = b.velocity.reject_from_normalized(n) + n * bs2
    end
  end

  def window_size_default
    V[800, 800]
  end

  show
end