📐
直線に埋まった円を補正する
ここだけの用語
| 用語 | 意味 |
|---|---|
| 表 | 上側。ab の法線側。矢印の右側。 |
| 裏 | 下側。直線 ab の法線の反対側。矢印の左側。 |
考え方
- 直線と円心の距離を求める
- 距離から半径を引いた値を求める
- 負であれば埋まっている
- 直線の法線方向に押し返す
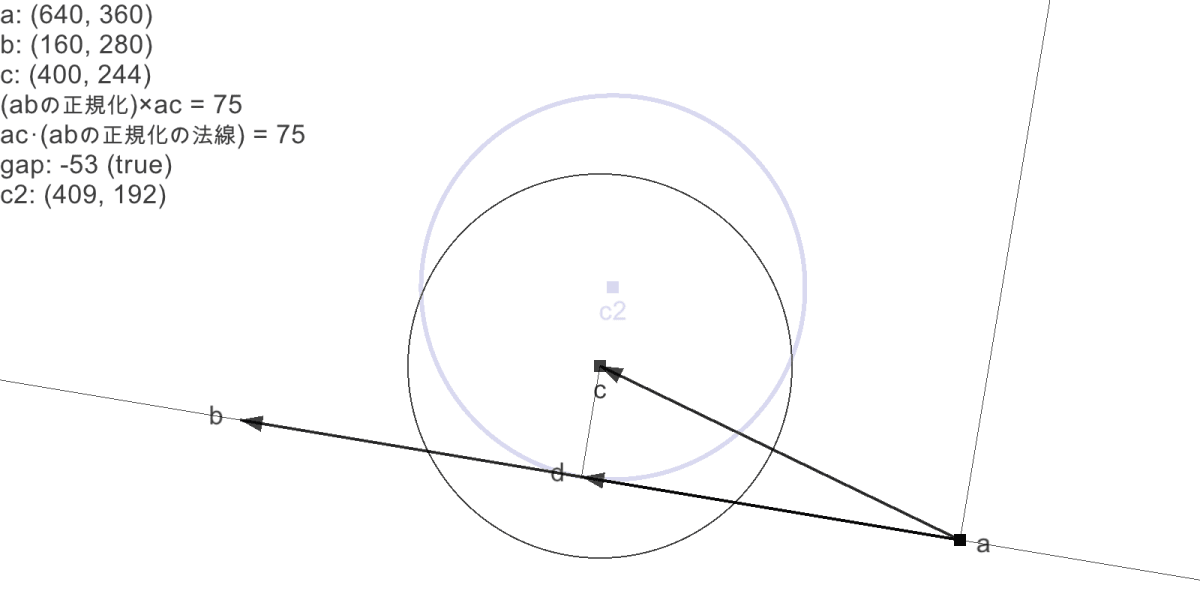
事前にわかっている情報
直線
a = V[640.0, 360.0]
b = V[160.0, 280.0]
円
c = V[400.0, 244.0]
radius = 128
最短距離を求める
ab = b - a # => (-480.0, -80.0)
ac = c - a # => (-240.0, -116.0)
abn = ab.normalize # => (-0.9863939238321436, -0.16439898730535726)
distance = abn.cross(ac) # => 74.96593821124291
distance = ac.dot(abn.perp) # => 74.96593821124291
二つの方法がある。ac を斜辺とし「直線 ab を地面」としたとき最短距離(直立射影)は外積で求まる。ac を斜辺とし「直線 ab の法線を地面」としたとき最短距離(正射影)は内積で求まる。どちらでも同じだが外積を使う方が自然な感じはする。
また、このときの distance の符号で裏表どちらに円心があるかが分かる。
めり込んでいるか判定する
浮動小数点の誤差の影響で補正後でもめり込んでいると判定されるのを防ぐため四捨五入するのが望ましい。
gap = distance - radius # => -53.034061788757086
gap.round.negative? # => true
もし「めり込んだと判定する限度は半径の長さまで」としたい場合は次の条件を追加する。
-gap < radius # => true
このあたりの判定がややこしいの改善の余地あり (後述)
押し返す
法線の方向ベクトル
abn.perp # => (0.16439898730535726, -0.9863939238321436)
に、埋まったぶん
-gap # => 53.034061788757086
を掛ければ押し返す分のベクトル
abn.perp * -gap # => (8.718746050761409, -52.312476304568456)
になるので現在の位置に足せば補正後の値になる。
c2 = c + abn.perp * -gap # => (408.7187460507614, 191.68752369543154)
いったんまとめ
a = V[640.0, 360.0]
b = V[160.0, 280.0]
c = V[400.0, 244.0]
radius = 128
ab = b - a # => (-480.0, -80.0)
ac = c - a # => (-240.0, -116.0)
abn = ab.normalize # => (-0.9863939238321436, -0.16439898730535726)
distance = abn.cross(ac) # => 74.96593821124291
gap = distance - radius # => -53.034061788757086
if gap.round.negative?
c2 = c + abn.perp * -gap # => (408.7187460507614, 191.68752369543154)
end
ここで終わってもいいが後のことを考えたらもう少し進めたい。
リファクタリング
条件判断をより柔軟にするため円と直線の位置関係を正規化する。
t = distance / radius # => 0.5856713922753353
正規化といっても「距離 ÷ 半径」をやっているだけ。だが、これで円と直線の位置関係が t を見るだけでわかるようになる。
| t | 表裏 | めり込み | 隣接 | 孤立 |
|---|---|---|---|---|
| 1.1 | 表 | ○ | ||
| 1.0 | 表 | ○ | ||
| 0.9 | 表 | ○ | ||
| 0.1 | 表 | ○ | ||
| 0.0 | ◎ | |||
| -0.1 | 裏 | ○ | ||
| -0.9 | 裏 | ○ | ||
| -1.0 | 裏 | ○ | ||
| -1.1 | 裏 | ○ |
なので、どれだけ壁にめり込んでも表に補正させたければ
t < 1.0 # => true
とすればよいし、めり込みは半径分だけとしたければ
(0...1).cover?(t) # => true
とすればよい。
続いて直線との交点を t から求める場合は、
d2 = c - abn.perp * radius * t # => (387.6756756756757, 317.94594594594594)
とする。この位置は普通に斜辺と直線の内積でも求まる。[1]
a + ac.project_onto_normalized(abn) # => (387.67567567567573, 317.94594594594594)
続いて押し返す計算で gap を使ったときは、
-gap # => 53.034061788757086
c2 = c + abn.perp * -gap # => (408.7187460507614, 191.68752369543154)
となっていた。しかし、ここでは t しかないので t から gap 相当に変換して計算する。
(1 - t) * radius # => 53.034061788757086
c2 = c + abn.perp * (1 - t) * radius # => (408.7187460507614, 191.68752369543154)
これで gap 変数ががなくても補正後の位置が求まる。
まとめ
表のみ

a = V[640.0, 360.0]
b = V[160.0, 280.0]
c = V[400.0, 244.0]
radius = 128
ab = b - a # => (-480.0, -80.0)
ac = c - a # => (-240.0, -116.0)
abn = ab.normalize # => (-0.9863939238321436, -0.16439898730535726)
distance = abn.cross(ac) # => 74.96593821124291
t = distance / radius # => 0.5856713922753353
if t < 1.0
c2 = c + abn.perp * (1 - t) * radius # => (408.7187460507614, 191.68752369543154)
end
両面対応
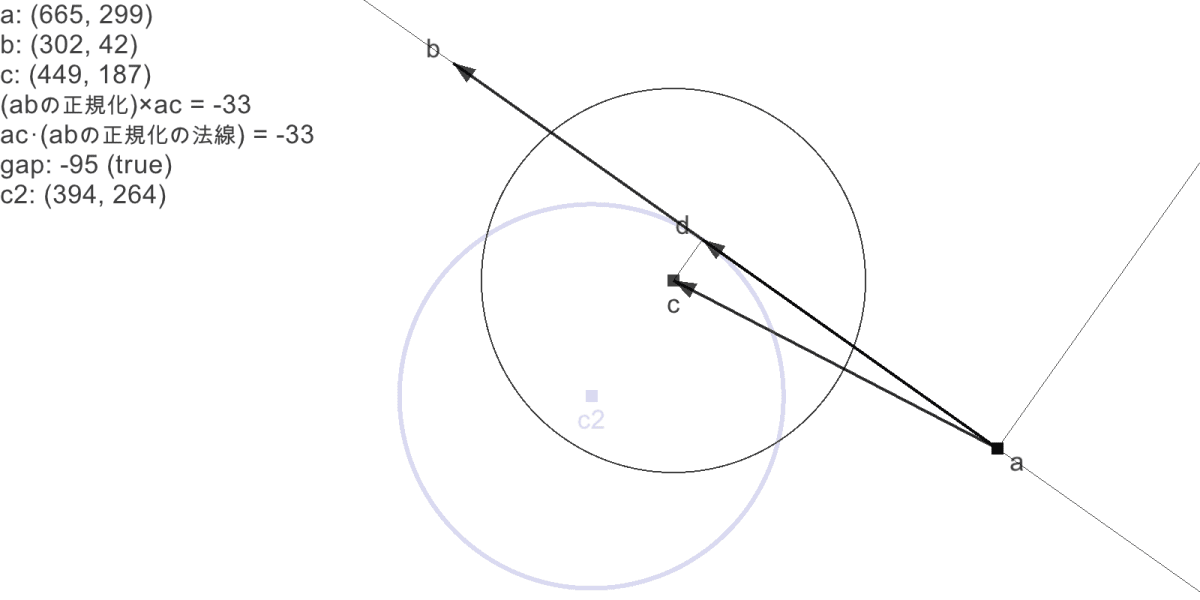
a = V[665.0, 299.0]
b = V[302.0, 42.0]
c = V[449.0, 187.0]
radius = 128
ab = b - a # => (-363.0, -257.0)
ac = c - a # => (-216.0, -112.0)
abn = ab.normalize # => (-0.816157022287791, -0.5778301783139457)
distance = abn.cross(ac) # => -33.40173201957967
sign = distance.positive? ? 1 : -1 # => -1
t = distance / radius # => -0.26095103140296616
if t.abs < 1.0
c2 = c + abn.perp * (1 - t.abs) * radius * sign # => (394.3382659446833, 264.20704070848234)
end
コード
class App < Base
def initialize
super
a = window_wh * V[0.8, 0.90] # => (640.0, 360.0)
b = window_wh * V[0.2, 0.70] # => (160.0, 280.0)
c = window_wh * V[0.5, 0.61] # => (400.0, 244.0)
@points.concat([a, b, c])
@mode = 0
@mode2 = 0
@mode3 = 1
end
def button_down(id)
super
if id == Gosu::KB_Z
@mode = @mode.next.modulo(2)
end
if id == Gosu::KB_X
@mode2 = @mode2.next.modulo(2)
end
if id == Gosu::KB_C
@mode3 = @mode3.next.modulo(2)
end
end
def draw
super
radius = 128.0
a, b, c = @points
ab = b - a
abn = ab.normalize
ac = c - a
d = nil
# 確認用
if true
if @mode == 0
# 直線を底辺と考える
ad = ac.project_onto_normalized(abn)
else
# 法線を底辺と考える
ad = ac.project_onto_normalized(abn.perp)
end
d = a + ad
end
if @mode == 0
# 外積を使う場合
distance = abn.cross(ac)
else
# 内積を使う場合
distance = ac.dot(abn.perp)
end
sign = distance.positive? ? 1 : -1
if @mode3 == 0
if @mode2 == 0
vputs "表面のみ対応"
gap = distance - radius
if gap.round.negative?
c2 = c + abn.perp * -gap
end
else
vputs "裏面対応"
gap = distance * sign - radius
if -gap < radius
if gap.round.negative?
c2 = c + abn.perp * -gap * sign
end
end
end
else
if @mode2 == 0
vputs "tで計算 - 表面のみ対応"
t = distance / radius
d2 = c - abn.perp * radius * t
point_draw d2, color: :red
if t < 1.0
c2 = c + abn.perp * (1 - t) * radius
end
else
vputs "tで計算 - 両面のみ対応"
t = distance / radius
d2 = c - abn.perp * radius * t
point_draw d2, color: :red
if t.abs < 1.0
c2 = c + abn.perp * (1 - t.abs) * radius * sign
end
end
end
vputs "a: #{a.round}"
vputs "b: #{b.round}"
vputs "c: #{c.round}"
vputs "d: #{d.round}"
vputs "d2: #{d2.round}" if d2
if true
vputs "(abの正規化)×ac = #{abn.cross(ac).round}"
vputs "ac・(abの正規化の法線) = #{ac.dot(abn.perp).round}"
vputs "gap: #{gap.round} (#{gap.round.negative?})" if gap
vputs "t: #{t.round(2)} (#{(0.0...1.0).cover?(t.round(2))})" if t
line_draw(a, a + ab.perp.clamp_length_min(wh.length))
line_draw(a, c)
line_draw(a, b, infinity: true)
vector_draw(a, c, "", "")
if d
line_draw(c, d)
vector_draw(a, d, "", "d")
end
end
# 円
if true
point_draw(c)
arrow_head(c + V.from_angle(270.deg_to_rad), c, "c")
circle_draw(c, radius)
if c2
circle_draw(c2, radius, color: :blue_light, line_width: 3)
point_draw(c2, color: :blue_light)
arrow_head(c2 + V.from_angle(270.deg_to_rad), c2, "c2", color: :blue_light)
vputs "c2: #{c2.round}"
end
end
# 直線
vector_draw(a, b, "a", "b")
end
def window_size_default
V[800, 400]
end
show
end
-
もし直線を線分と見なす場合は、線分の両端から交点に向かうベクトル同士の内積をとれば線分内で接触しているか判定できる ↩︎
Discussion