📐

動く円と円の衝突と反発ベクトルの求め方

2023/10/04に公開

Ruby

物理

内積

tech

考え方

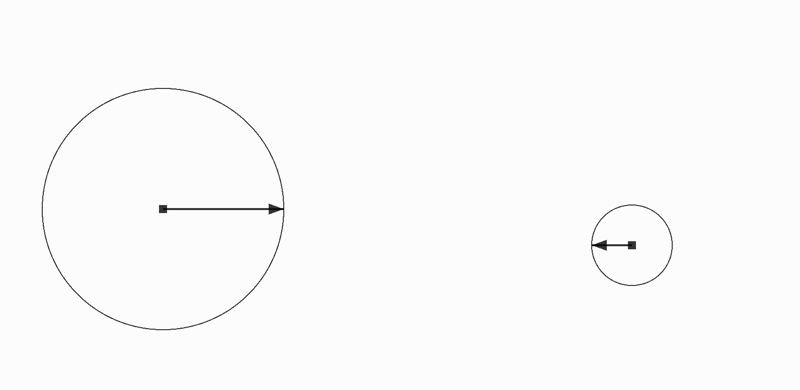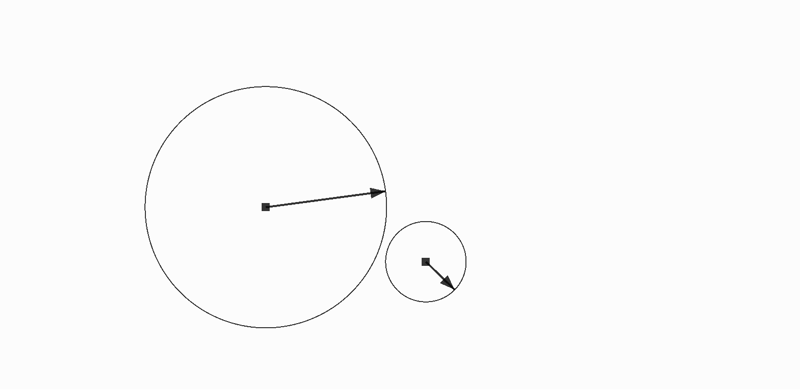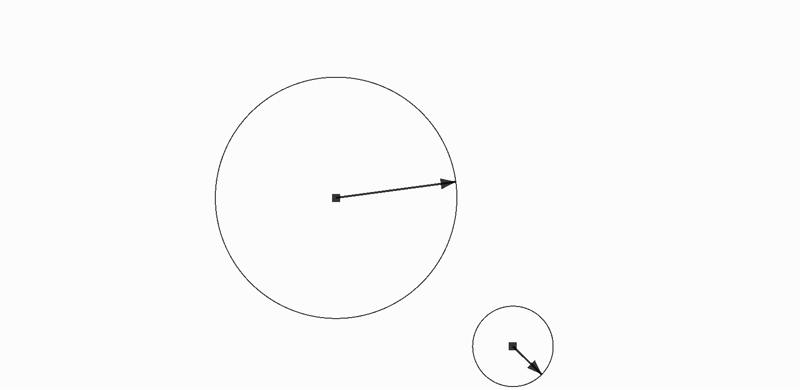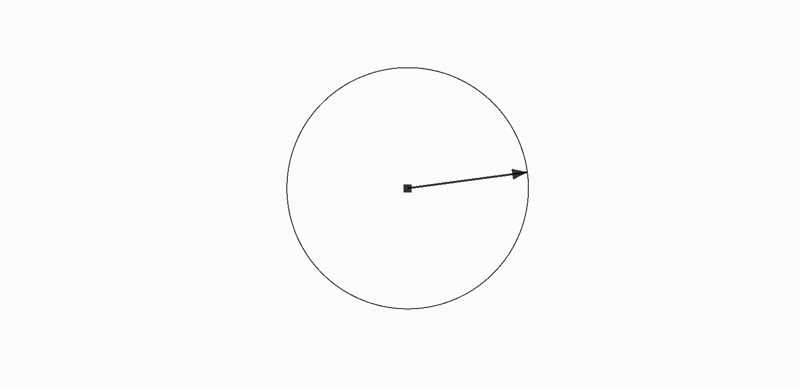
黒の方向に向かっているときに衝突したので緑の方向に反発する

円心と円心を結ぶ直線を地面と考える
速度ベクトルから地面に平行な強さのみを出す
その強さを1次元の速度と考えて反発後の速度を求める
反発後の速度を地面に平行なベクトルに戻す
速度ベクトルの直立成分に足す

事前にわかっているパラメータ

変数	意味
a	位置
ar	半径
am	質量 (PI * ar**2)
av	速度ベクトル

a   # => (260.0, 208.0)
ar  # => 150
am  # => 70685.83470577035
av  # => (76.0, -112.0)

b も a の命名ルールと同様とする。

b   # => (558.4, 192.0)
br  # => 150
bm  # => 70685.83470577035
bv  # => (-94.39999999999998, -96.0)

a b 間のベクトルを求める

ab = b - a        # => (298.4, -16.0)
n = ab.normalize  # => (0.9985655774411905, -0.05354239021132389)

正規化したのを n としておく。

当たり判定 (オプション)

gap = ab.length - ar - br  # => -1.1713534481675651
gap.round.negative?        # => true

当たっている前提で進めてきたが必要であれば判定する。負であれば衝突している。round しているのは小数点誤差の災いを回避するため。

円を離す (オプション)

len = -gap                      # => 1.1713534481675651
a                               # => (260.0, 208.0)
b                               # => (558.4, 192.0)
a += n * len * -bm / (am + bm)  # => (259.41516338382144, 208.03135853169857)
b += n * len *  am / (am + bm)  # => (558.9848366161785, 191.96864146830143)

今回のように円と円が離れた状態から衝突するケースしかないのであればこれは必要ない。しかし、円を配置した時点で他の円と重なっていたり、他の物体に押されて重なってしまった場合は、衝突後の速度ベクトルを加算しても円と円は衝突したままなので永遠に衝突した状態になる。これを解消するには円と円が重ならない位置まで双方を押し返す。

速度ベクトルを分割する

ここからがおもしろいところで直線 ab に対して垂直なベクトル(avx)と水平なベクトル(avy)に分ける。これは円同士が横に並んでいて速度ベクトルが (2, 3) だったとすれば (2, 0) と (0, 3) に分けるのと同じ。しかし実際はぴったり横には並んでいないので位置関係から算出する。それにはまず正射影の長さを求める。

as = av.dot(n)  # => 81.88773158919875

この正射影の長さが相手の円に対する当たりの強さになる。たとえば、剛速球でもファウルチップならバットへの衝撃は非常に小さい。

次に強さから垂直ベクトルを求める。

avx = n * as  # => (81.77026997971747, -4.384464878269033)

次に速度ベクトルから垂直ベクトルを引くと水平ベクトルが求まる。

avy = av - avx  # => (-5.770269979717469, -107.61553512173097)

このあたり、わかりやすさを優先するなら専用のメソッド使った方が意図が明確になる。それぞれ正射影と直立射影として求まる。

avx = av.project_onto_normalized(n)  # => (81.77026997971747, -4.384464878269033)
avy = av.reject_from_normalized(n)   # => (-5.770269979717469, -107.61553512173097)

b も同様に計算する。

bs = bv.dot(n)                       # => -89.12452105016126
bvx = bv.project_onto_normalized(n)  # => (-88.99667882662382, 4.771939883465085)
bvy = bv.reject_from_normalized(n)   # => (-5.403321173376156, -100.77193988346508)

ここで b 側から見ているからといって対照的に直線を ba としてはいけない。a も b も直線 ab に対して計算することで当りの強さに符号がつく。求まった as と bs を見ると符号によって対向しているのがわかる。

as  # => 81.88773158919875
bs  # => -89.12452105016126

ここからは一次元の話になる。いったん円のことは忘れて一車線で二つの車が対向して衝突したところをイメージする。

反発係数を決める

e = 0.8

図で avx に対して avx2 が少し短かくなっているのは 0.2 だけ運動量が減ったため。

反発する

変数	意味
e	反発係数
am	車aの質量
as	車aの速度
bm	車bの質量
bs	車bの速度
as2	車aの速度(衝突後)
bs2	車bの速度(衝突後)

e   # => 0.8
am  # => 70685.83470577035
as  # => 81.88773158919875
bm  # => 70685.83470577035
bs  # => -89.12452105016126

as2 = (am*as + bm*bs - (e * bm * (as - bs))) / (am + bm)  # => -72.02329578622528
bs2 = (am*as + bm*bs + (e * am * (as - bs))) / (am + bm)  # => 64.78650632526276

公式に当てはめると反発後の速度が求まる。

速度を直線上のベクトルに変換する

ここで二次元の世界に戻る。直線 ab の傾きを反映させるため、反発後の速度であるスカラーを直線の傾きを持ったベクトルに変換する。単に「新しい垂直成分のベクトル」とイメージするとわかりやすい。

avx2 = n * as2  # => (-71.9199839459897, 3.8562994072916736)
bvx2 = n * bs2  # => (64.69357509908335, -3.4688244020956223)

念のために確認すると、垂直成分のベクトルの長さは反発後の速度の絶対値と一致しているのがわかる。

as2          # => -72.02329578622528
avx2.length  # => 72.02329578622526

bs2          # => 64.78650632526276
bvx2.length  # => 64.78650632526275

速度ベクトルに戻す

av2 = avy + avx2  # => (-77.69025392570717, -103.7592357144393)
bv2 = bvy + bvx2  # => (59.29025392570719, -104.2407642855607)

分けておいた水平成分に新しい垂直成分を足すと反発後の速度ベクトル(緑)が求まる。

いったん計算手順まとめ

速度ベクトルから垂直成分のスカラーを出す
速度ベクトルから垂直水平ベクトルに分ける
垂直成分のスカラーから反発後のスカラーを求める
そのスカラーから垂直ベクトルに変換する
そのベクトルを水平ベクトルと合わせる

as = av.dot(n)                                            # => 81.88773158919875
avx = n * as                                              # => (81.77026997971747, -4.384464878269033)
avy = av - avx                                            # => (-5.770269979717469, -107.61553512173097)
bs = bv.dot(n)                                            # => -89.12452105016126
bvx = n * bs                                              # => (-88.99667882662382, 4.771939883465085)
bvy = bv - bvx                                            # => (-5.403321173376156, -100.77193988346508)
as2 = (am*as + bm*bs - (e * bm * (as - bs))) / (am + bm)  # => -72.02329578622528
bs2 = (am*as + bm*bs + (e * am * (as - bs))) / (am + bm)  # => 64.78650632526276
avx2 = n * as2                                            # => (-71.9199839459897, 3.8562994072916736)
bvx2 = n * bs2                                            # => (64.69357509908335, -3.4688244020956223)
av2 = avy + avx2                                          # => (-77.69025392570717, -103.7592357144393)
bv2 = bvy + bvx2                                          # => (59.29025392570719, -104.2407642855607)

考え方の最適化

垂直成分はスカラーではなくベクトルのままでもよい。これまで方法はベクトル→スカラー→ベクトルと変換を行っていたがベクトルのままでも結果は同じになる。

速度ベクトルから垂直水平ベクトルに分ける
垂直ベクトルから反発後の垂直ベクトルを求める
そのベクトルを水平ベクトルと合わせる

avx = av.project_onto_normalized(n)                            # => (81.77026997971747, -4.384464878269033)
bvy = bv.reject_from_normalized(n)                             # => (-5.403321173376156, -100.77193988346508)
avx2 = (am*avx + bm*bvx - (e * bm * (avx - bvx))) / (am + bm)  # => (-71.9199839459897, 3.8562994072916736)
bvx2 = (am*avx + bm*bvx + (e * am * (avx - bvx))) / (am + bm)  # => (64.69357509908335, -3.4688244020956214)
av2 = avy + avx2                                               # => (-77.69025392570717, -103.7592357144393)
bv2 = bvy + bvx2                                               # => (59.29025392570719, -104.2407642855607)

ただし 2.65 倍遅くなる。ベクトルのままでもよいが、より高速に処理するならスカラーで計算した方が速い。

疑問: 反発係数 1.0 だと単純な反射ベクトルと同じ？

同じではない。

質量を考慮したロジックにしても結局、反発係数が 1.0 だと意味がなさそうに思えてきて、単に反射ベクトルを求める方法に置き換えたくなってくる。

av.bounce(n)  # => (-87.54053995943494, -103.23107024346193)
bv.bounce(n)  # => (83.59335765324766, -105.54387976693017)

が、それは間違い。なぜ間違っているかは二つの円の速度ベクトルを 100 と 0 と考えるとわかりやすい。質量を考慮した場合 100 と 0 が衝突すると 0 と 100 になる。一方、単に反射ベクトルを求めた場合は -100 と 0 になる。したがって「反発係数 1.0 で質量を考慮したとき」と「単純な反射ベクトル」は異なる。

コード

ベクトル確認

class App < Base
  def initialize
    super

    a0 = window_wh * V[0.325, 0.52]                             # => (260.0, 312.0)
    a1 = window_wh * V[0.420, 0.24]                             # => (336.0, 144.0)
    b0 = window_wh * V[0.698, 0.48]                             # => (558.4, 288.0)
    b1 = window_wh * V[0.580, 0.24]                             # => (463.99999999999994, 144.0)
    @points = [a0, a1, b0, b1]
  end

  def draw
    super

    a0, a1, b0, b1 = @points
    ab = b0 - a0
    n = ab.normalize

    # a
    if true
      ar = 150
      am = PI * ar**2
      av = a1 - a0
      as = av.dot(n)

      avx = av.project_onto_normalized(n)
      avy = av.reject_from_normalized(n)

      circle_draw(a0, ar, color: :grey)
      vector_draw(a0, a1, "", "", name: "av")
      vector_draw(a0, a0 + avx, "", "", color: :blue, name: "avx")
      vector_draw(a0, a0 + avy, "a", "", color: :red, name: "avy")
      line_draw(a1, a0 + avx, color: :grey, infinity: true)

      vputs "av: #{av.round}"
      vputs "avx: #{avx.round}"
      vputs "ar: #{ar}"
      vputs "as: #{as.round}"
      vputs
    end

    # b
    if true
      br = 150
      bm = PI * br**2
      bv = b1 - b0
      bs = bv.dot(n)

      bvx = bv.project_onto_normalized(n)
      bvy = bv.reject_from_normalized(n)

      circle_draw(b0, br, color: :grey)
      vector_draw(b0, b1, "", "", name: "bv")
      vector_draw(b0, b0 + bvx, "", "", color: :blue, name: "bvx")
      vector_draw(b0, b0 + bvy, "b", "", color: :red, name: "bvy")
      line_draw(b1, b0 + bvx, color: :grey, infinity: true)

      vputs "bv: #{bv.round}"
      vputs "bvx: #{bvx.round}"
      vputs "br: #{br}"
      vputs "bs: #{bs.round}"
      vputs
    end

    gap = ab.length - ar - br

    vputs "ab: #{ab.round}"
    vputs "n: #{n.round(2)}"
    vputs "ab.perp: #{ab.perp.round}"
    vputs "ab.length: #{ab.length.round}"
    vputs "gap: #{gap.round}"
    vputs

    if true
      # 質量を無視して反発した場合
      point_draw(a0 + av.bounce(n), color: :white_ter)
      point_draw(b0 + bv.bounce(n), color: :white_ter)
    end

    if true
      e = 0.8
      vputs "e: #{e}"

      as2 = (am*as + bm*bs - (e * bm * (as - bs))) / (am + bm)  # => -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034, -65.37409540266034
      bs2 = (am*as + bm*bs + (e * am * (as - bs))) / (am + bm)  # => 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476, 72.0463830681476

      vputs "as2: #{as2.round}"
      vputs "bs2: #{bs2.round}"

      avx2 = n * as2
      bvx2 = n * bs2

      vputs "avx2: #{avx2.round}"
      vputs "bvx2: #{bvx2.round}"

      av2 = avy + avx2
      bv2 = bvy + bvx2

      vputs "av2: #{av2.round}"
      vputs "bv2: #{bv2.round}"

      vector_draw(a0, a0 + avx2, "", "", name: "avx2", color: :magenta)
      vector_draw(b0, b0 + bvx2, "", "", name: "bvx2", color: :magenta)

      vector_draw(a0, a0 + av2, "", "", name: "av2", color: :green)
      vector_draw(b0, b0 + bv2, "", "", name: "bv2", color: :green)
    end

    line_draw(a0, b0, color: :grey, infinity: true)
  end

  show
end

シミュレーション

class Ball
  attr_accessor :location
  attr_accessor :velocity
  attr_accessor :radius
  attr_accessor :mass

  def update
    @location += @velocity
  end

  def draw
    $app.circle_draw(@location, @radius)
    $app.vector_draw(@location, @location + @velocity.clamp_length_min(@radius))
  end
end

class App < Base
  attr_accessor :balls

  def initialize
    super

    preset1
  end

  def preset1
    @balls = []

    @balls << Ball.new.tap do |e|
      e.location = V[0.20, 0.47] * window_wh
      e.velocity = V[1.0, 0.0]
      e.radius   = 120.0
      e.mass     = e.radius**2
    end

    @balls << Ball.new.tap do |e|
      e.location = V[0.80, 0.53] * window_wh
      e.velocity = V[-2.5, 0.0]
      e.radius   = 40.0
      e.mass     = e.radius**2
    end
  end

  def button_down(id)
    super

    if id == Gosu::KB_R
      preset1
    end
  end

  def update
    super

    @balls.combination(2) { |a, b| rebound(a, b) }
    @balls.each(&:update)
  end

  def draw
    super

    @balls.each(&:draw)
  end

  def rebound(a, b)
    ab = b.location - a.location
    gap = ab.length - a.radius - b.radius
    if gap.round.negative?
      len = -gap
      n = ab.normalize

      am = a.mass
      bm = b.mass

      a.location = a.location + n * len * -bm / (am + bm)
      b.location = b.location + n * len *  am / (am + bm)

      as = a.velocity.dot(n)
      bs = b.velocity.dot(n)

      e = 0.1
      as2 = (am*as + bm*bs - (e * bm * (as - bs))) / (am + bm)
      bs2 = (am*as + bm*bs + (e * am * (as - bs))) / (am + bm)

      a.velocity = a.velocity.reject_from_normalized(n) + n * as2
      b.velocity = b.velocity.reject_from_normalized(n) + n * bs2

      true
    end
  end

  show
end