壁に衝突した物体の本当の反発ベクトル

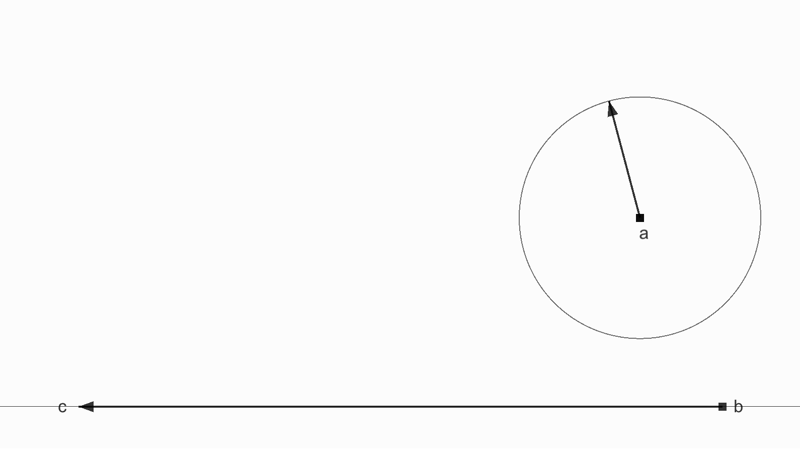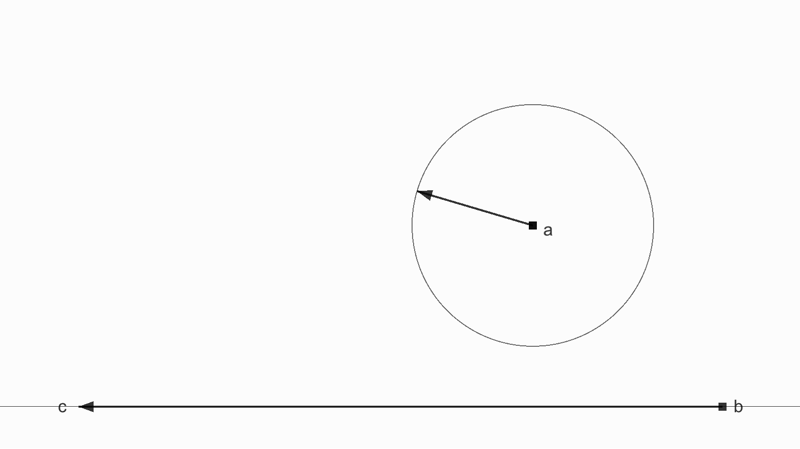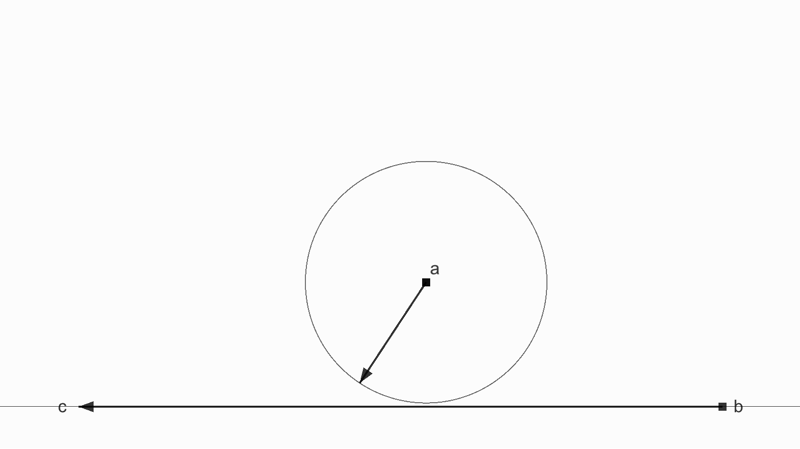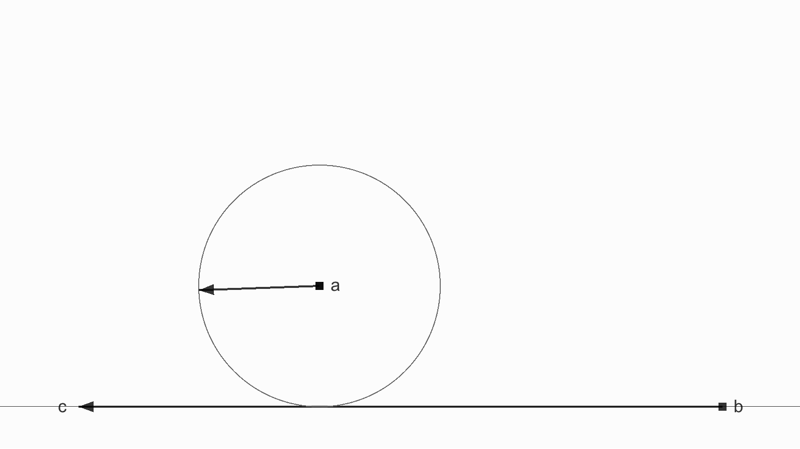
縦方向の力は弱まっていくが横方向の力は減らない

ただの反発ベクトルとは異なる

反発係数 0.5 で黒の方向で衝突した物体の速度ベクトルは緑の方に反発する。なぜなら、反射は壁に対して垂直方向のみが影響を受けるから。

続いてこちらの記事の固定壁に質点を当てるを実証していく。

http://marupeke296.com/COL_MV_No2_WallVsBall.html

パラメータ

反発係数

e = 0.5

物体

a = V[400.0, 200.0]             # 中心
v = V[640.0,  87.0]             # 中心 + 速度ベクトル
av = v - a  # => (240.0, -113.0)

円か点かは今回関係がないので点と考えてもいい。

壁

c = V[548.0, 370.0]
b = V[548.0,  30.0]
bc = c - b          # => (0.0, 340.0)
bcn = bc.normalize  # => (0.0, 1.0)

壁の法線の正規化

n = bcn.perp  # => (-1.0, 0.0)

計算方法

壁に垂直な成分を抽出する。

avx = n * av.dot(n)                  # => (240.0, -0.0)
avx = av.project_onto_normalized(n)  # => (240.0, -0.0)

壁に水平な成分を抽出する。

avy = av - avx                      # => (0.0, -113.0)
avy = av.reject_from_normalized(n)  # => (0.0, -113.0)

壁に垂直な成分のみにマイナスの反発係数を掛ける。

avx2 = -e * avx  # => (-120.0, 0.0)

壁に水平な成分と合体して元に戻す。

av2 = avx2 + avy  # => (-120.0, -113.0)

整理する

avx = n * av.dot(n)  # => (240.0, -0.0)
avy = av - avx       # => (0.0, -113.0)
avx2 = -e * avx      # => (-120.0, 0.0)
av2 = avx2 + avy     # => (-120.0, -113.0)

を、av2 = の右辺に展開すると、

av2 = -e * n * av.dot(n) + av - n * av.dot(n)  # => (-120.0, -113.0)
av2 = av - e * n * av.dot(n) - n * av.dot(n)   # => (-120.0, -113.0)
av2 = av - (e * n + n) * av.dot(n)             # => (-120.0, -113.0)

となり、最後は

av2 = av - n * av.dot(n) * (1 + e)  # => (-120.0, -113.0)

となる。

単なる反射ベクトルとの違いを再度確認する

元の速度ベクトル(黒)

av  # => (240.0, -113.0)

単なる反発ベクトルに反発係数の影響を受けたベクトル(灰色)

av3 = (av - n * av.dot(n) * 2) * e                  # => (-120.0, -56.5)
av3 = (av - av.project_onto_normalized(n) * 2) * e  # => (-120.0, -56.5)
av3 = av.bounce(n) * e                              # => (-120.0, -56.5)

垂直方向のみに反発係数の影響を受けたベクトル(緑)

av2 = av - n * av.dot(n) * (1 + e)                  # => (-120.0, -113.0)
av2 = av - av.project_onto_normalized(n) * (1 + e)  # => (-120.0, -113.0)

単なる反発ベクトルは元の速度ベクトルの半分になっているだけだが、垂直方向のみに反発係数の影響を受けたベクトルは水平方向の強さを維持しているのが計算結果からもわかる。

計算式まとめ

速度

velocity  # => (240.0, -113.0)

反発係数 (摩擦係数)

e  # => 0.5

壁からの法線

n  # => (-1.0, 0.0)

反発後の速度

velocity - n * velocity.dot(n) * (1 + e)                  # => (-120.0, -113.0)
velocity - velocity.project_onto_normalized(n) * (1 + e)  # => (-120.0, -113.0)

反発係数 1.0 のとき単なる反射ベクトルと同じか？

同じ。今回の計算では運動量が壁に移動したりしないため反発係数 1.0 のときは同じになる。だからといって普通の反発ベクトルを求める式に書き換えるメリットは少ない。どちらも内積を1回やってる程度で計算量はほとんど変わらない。正確には単なる反射ベクトルの計算量より 1.09 倍遅い。

反発係数は摩擦係数と同じか？

おそらく同じ。Nature of Code では垂直抗力の大きさを 1.0 と仮定しているものの行っていることはだいたい同じ。

c = 0.01                        # 摩擦係数
normal = 1.0                    # 壁への当たりの強さ
friction_mag = c * normal
friction = -velocity.normalize * friction_mag
acceleration += friction / mass # 質量を考慮して加速度に足す

ただ acceleration に足していいのだろうか？ 上にも書いたけど acceleration に足すのはまずいような気がする。

壁が動いている場合

続いて迫り来る壁を実証する。

変数	意味	値
e	反発係数	1.0
v	物体の速度ベクトル	2.0
w	壁の速度ベクトル	-8.0

e = 1.0
v = V[2.0, 0.0]
w = V[-8.0, 0.0]

このとき相対速度は v - w になる。

相対速度 = v - w  # => (10.0, 0.0)

確かに自分が 2 で進んでいところに相手が 8 で向かってきたら 10 のスピードに感じる。ここまでは問題ない。そこで相手は止まっていて自分は 10 のスピードで進んでいると考える。したがって v を v - w に置き換える。

上の方で求めた式

v - (1 + e) * n * v.dot(n)  # => (-2.0, 0.0)

の v を v - w に置き換えると

(v - w) - (1 + e) * n * (v - w).dot(n)  # => (-10.0, 0.0)

となり、物体は相手の速度も足して反転したのがわかる。勘違いしていなければここで終わってよさそうだが元記事には続きがある。

実際には壁も動いていますので、それを元に戻す必要があります。これはv'にvWを足し算するだけです。

どういうことだ……？

実際に w を足すと -18 になってしまう。

(v - w) - (1 + e) * n * (v - w).dot(n) + w  # => (-18.0, 0.0)

元記事の最下段の導出式を計算結果も、

v - (1 + e) * n * (v - w).dot(n)  # => (-18.0, 0.0)

となってしまう。

2 の速度で来た卓球の球を 8 の力で打ったとき 18 にもなるだろうか？

……わからん。

シミュレーション

class Wall
  attr_accessor :p0
  attr_accessor :p1

  def initialize
    @p0 = $app.window_wh * V[0.9, 0.85]
    @p1 = $app.window_wh * V[0.1, 0.90]
  end

  def draw
    $app.line_draw(p0, p1, infinity: true)
    $app.vector_draw(p0, p1, "b", "c")
  end
end

class Ball
  attr_accessor :location
  attr_accessor :velocity
  attr_accessor :restitution

  def initialize
    @location = $app.window_wh * 0.5
    @velocity = V.zero
    @acceleration = V.zero
    @radius = 120
    @restitution = 1.0
  end

  def draw
    b = $app.wall.p0
    c = $app.wall.p1
    bc = c - b
    n = bc.normalize.perp

    ba = @location - b
    distance = ba.dot(n)
    t = distance / @radius

    if t < 1.0
      @location.replace(@location + n * (1 - t) * @radius)                              # 補正方法1
      # @location.replace((b + ba.project_onto(bc)) + (n * @radius))                      # 補正方法2
      @velocity = @velocity - @velocity.project_onto_normalized(n) * (1 + @restitution) # 反発
    end

    if !$app.pause
      @acceleration += $app.gravity
      @velocity += @acceleration
      @location.replace(@location + @velocity)
      @location.replace(@location.modulo($app.window_wh))
      @acceleration = V.zero
    end

    $app.vputs "velocity: #{@velocity.length.round(2)} #{@velocity.round(2)}"
    $app.point_draw(@location)
    $app.circle_draw(@location, @radius, color: :grey)
    $app.vector_draw(@location, @location + @velocity.clamp_length_min(@radius), "a")
  end
end

class App < Base
  attr_accessor :ball
  attr_accessor :wall
  attr_accessor :gravity
  attr_accessor :pause

  def initialize
    super
    @pause = true
    preset1
  end

  def preset1
    @gravity = V[0.0, 0.03]

    @ball = Ball.new
    @ball.location = window_wh * V[0.8, 0.4]
    @ball.velocity = V[-0.5, -2.0]
    @ball.restitution = 0.7

    @wall = Wall.new
    @wall.p0 = window_wh * V[0.9, 0.7]
    @wall.p1 = window_wh * V[0.1, 0.7]

    @points = [@ball.location, @wall.p0, @wall.p1]
  end

  def button_down(id)
    super

    case id
    when Gosu::KB_R
      preset1
    when Gosu::KB_P
      @pause ^= true
    end
  end

  def draw
    super

    @wall.draw
    @ball.draw

    vputs "[p] pause: #{@pause}"
  end

  show
end

ベクトル確認

class App < Base
  def initialize
    super

    preset1
  end

  def preset1
    a = V[400.0, 200.0]
    v = V[640.0,  87.0]
    b = V[548.0,  30.0]
    c = V[548.0, 370.0]
    @points = [a, v, b, c]
  end

  def preset2
    a = V[400.0, 200.0]
    v = V[400.0, 200.0]
    b = V[677.0, 327.0]
    c = V[169.0, 365.0]
    d = V[558.0, 300.0]
    @points = [a, v, b, c, d]
  end

  def button_down(id)
    super

    case id
    when Gosu::KB_1
      preset1
    when Gosu::KB_2
      preset2
    end
  end

  def draw
    super

    a, v, b, c, d = @points
    bc = c - b
    bcn = bc.normalize
    n = bcn.perp

    vputs "a: #{a.round}"
    vputs "v: #{v.round}"
    vputs "b: #{b.round}"
    vputs "c: #{c.round}"
    vputs "d: #{d.round}" if d
    vputs

    ar = 150
    am = PI * ar**2
    av = v - a
    as = av.dot(n)

    ab = b - a
    ba = a - b
    (ba.cross(bcn) - ab.dot(n)).abs == 0 or raise

    # 補正する場合
    if true
      distance = ba.dot(n)
      t = distance / ar
      tt = a - n * ar * t
      point_draw tt, color: :blue
      if t < 1.0
        a2 = a + n * (1 - t) * ar
        if button_down?(Gosu::KB_Z) || true
          circle_draw(a2, ar, color: :blue_light)
        end
      end
    end

    avx = av.project_onto_normalized(n)
    avy = av.reject_from_normalized(n)

    e = 0.5
    as2 = -as * e
    avx2 = n * as2
    av2 = avy + avx2
    av2.abs_diff_eq(av - (1 + e) * n * av.dot(n), 0.001) or raise

    av3 = av.bounce(n) * e

    circle_draw(a, ar, color: :grey)
    vector_draw(a, v, "", "v", name: "av")
    vector_draw(a, a + avx, "", "", color: :blue, name: "avx")
    vector_draw(a, a + avy, "a", "", color: :red, name: "avy")
    line_draw(a, a + avx, color: :grey, infinity: true)

    line_draw(b, c, infinity: true)
    vector_draw(b, c, "b", "c")
    vector_draw(b, d, "", "d") if d

    vputs "av: #{av.round}"
    vputs "avx: #{avx.round}"
    vputs "ar: #{ar}"
    vputs "as: #{as.round}"
    vputs "e: #{e}"
    vputs "as2: #{as2.round}"
    vputs "avx2: #{avx2.round}"
    vputs "av2: #{av2.round}"
    vputs "av3: #{av3.round}"
    vputs

    vector_draw(a, a + av3, "", "", name: "av3", color: :grey_lighter)
    vector_draw(a, a + avx2, "", "", name: "avx2", color: :magenta)
    vector_draw(a, a + av2, "", "", name: "av2", color: :green)

    if d
      line_draw(b, b + n, infinity: true)
      bd = d - b
      bdx = bd.project_onto_normalized(n)
      vector_draw(b, b + bdx, "", "", name: "bdx", color: :blue)
    end
  end

  show
end