HAKUHIN's home page の「レイと線分とで当たり判定を取る」で紹介の謎の方程式を解明する
謎の方程式
ゲームプログラミングに関する技を紹介してくれている HAKUHIN's home page だが、レイと線分とで当たり判定を取る で紹介されている、

に、突き放された人は少なくない[1]だろう。それから十年以上経過し、ようやく解き明かしたので記しておく。
座標の扱いを統一する

座標を扱いやすいように位置ベクトル化する。
- レイの移動元座標 (x, y) → c
- 移動量を足した座標 (dx, dy) → d
a = V[463.99999999999994, 60.0] # 線分の端
b = V[720.0, 340.0] # 線分の端
c = V[384.0, 252.0] # レイの移動元座標
d = V[480.79999999999995, 246.0] # レイの移動先座標
もし、レイの速度ベクトルがほしい場合は
d - c # => (96.79999999999995, -6.0)
とすればいいのだが、毎回引き算するとわかりにくいので一括して求めておく。
cd = d - c # => (96.79999999999995, -6.0)
ab = b - a # => (256.00000000000006, 280.0)
ac = c - a # => (-79.99999999999994, 192.0)
ad = d - a # => (16.80000000000001, 186.0)
ca = a - c # => (79.99999999999994, -192.0)
謎の方程式を抽象化する
var d = -(ax * nx + ay * ny);
var t = -(nx * x + ny * y + d) / (nx * dx + ny * dy);
nx, ny は「直線 ab の法線の正規化」とのことなのでベクトル n として新しく定義する。また t の結果には関係がないが法線を逆向きにしておくと三角形の底辺の長さが正になって都合がよいのでマイナス符号をつける。
n = -ab.perp.normalize # => (0.7380288120022732, -0.6747691995449356)
次に位置ベクトル d があるのに一時的変数 d が出てくるとややこしいので d は k にしておく。また前述の通り、(x, y) は位置ベクトル c としたいので (c.x, c.y) とする。(dx, dy) は速度ベクトル cd としたいので (cd.x, cd.y) とする。
k = -(a.x * n.x + a.y * n.y) # => -301.9592167963586
t = -(n.x * c.x + n.y * c.y + k) / (n.x * cd.x + n.y * cd.y) # => 2.4983240223463703
ここで内積の公式 x1 * x2 + y1 * y2 を思い出すと上の式は内積の計算が三個所に展開されているのに気づく。そこで抽象化して dot メソッドを呼び出す表記に直す。
k = -a.dot(n) # => -301.9592167963586
t = -(n.dot(c) + k) / n.dot(cd) # => 2.4983240223463703
続いて二つめの式に k の値を代入して k を消す。
t = -(n.dot(c) - a.dot(n)) / n.dot(cd) # => 2.4983240223463703
続いて符号を整理して外側のマイナス符号を消す。
t = (a.dot(n) - n.dot(c)) / n.dot(cd) # => 2.4983240223463703
続いて内積は右辺と左辺を入れ替えることができるので dot(n) の形式に揃える。
t = (a.dot(n) - c.dot(n)) / cd.dot(n) # => 2.4983240223463703
続いて分子の a.dot(n) - c.dot(n) は ca.dot(n) に変換できるので、
a.dot(n) - c.dot(n) # => 188.59799127280948
ca.dot(n) # => 188.59799127280945
t = の式は、
t = ca.dot(n) / cd.dot(n) # => 2.49832402234637
まで短かくなる。
分子と分母は何の値か?
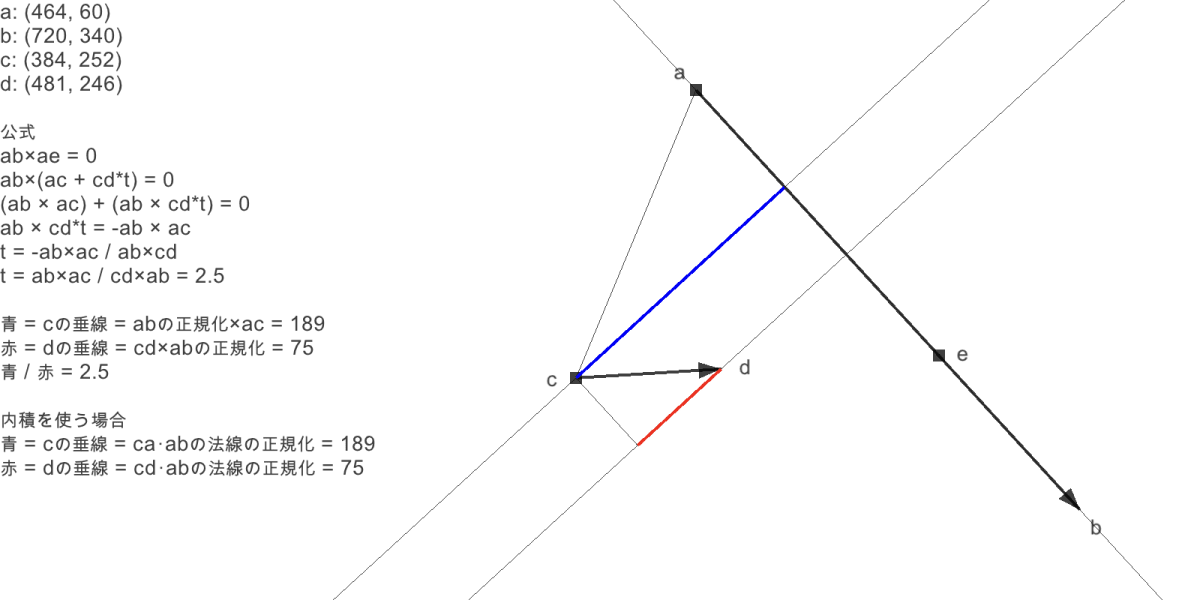
地面を正規化して内積を取るのは斜辺の正射影を求めたい場合なので、分子と分母は青と赤の長さを表したかったことがわかる。
- ca.dot(n) = 斜辺 ca からなる三角形の正射影 → 青
- cd.dot(n) = 斜辺 cd からなる三角形の正射影 → 赤
実際に確認すると
ca.dot(n) # => 188.59799127280945
cd.dot(n) # => 75.48980419908962
ca.dot(n) / cd.dot(n) # => 2.49832402234637
となっていて赤を約 2.5 倍すると青の長さになるのがわかる。
補足
高速化
単に t を求めるだけなら正規化を省略して
t = ca.dot(ab.perp) / cd.dot(ab.perp) # => 2.49832402234637
と書ける。
法線を出さない方法
t = ab.cross(ac) / cd.cross(ab) # => 2.49832402234637
直線 ab を地面と考えれば法線を出さなくても外積によって t は求まる。
まとめ
var d = -(ax * nx + ay * ny);
var t = -(nx * x + ny * y + d) / (nx * dx + ny * dy);
は、
n = -ab.perp.normalize # => (0.7380288120022732, -0.6747691995449356)
t = ca.dot(n) / cd.dot(n) # => 2.49832402234637
のことだった。
分子は「直線までの距離」で、分母は「直線までの一度に近づく距離」、簡単に言えば「速度」なので t = の式は「時間 = 距離 / 速度」の式でもある。
関連
コード
class App < Base
def initialize
super
self.width, self.height = V[800, 400]
a = window_wh * V[0.580, 0.150] # => (463.99999999999994, 60.0)
b = window_wh * V[0.900, 0.850] # => (720.0, 340.0)
c = window_wh * V[0.480, 0.630] # => (384.0, 252.0)
d = window_wh * V[0.601, 0.615] # => (480.79999999999995, 246.0)
@points.concat([a, b, c, d])
@mode = 1
@perp = 0
end
def button_down(id)
super
if id == Gosu::KB_Z
@mode = @mode.next.modulo(2)
end
if id == Gosu::KB_X
@perp = @perp.next.modulo(2)
end
end
def draw
super
a, b, c, d = @points
cd = d - c
ab = b - a
ac = c - a
ad = d - a
aa = a - a
ca = a - c
t = ab.cross(ac) / cd.cross(ab)
c_length = ab.normalize_or_zero.cross(ac)
d_length = cd.cross(ab.normalize_or_zero)
e = c.lerp(d, t)
xy = V[0, 0]
dd = V[10, 10]
vputs "a: #{a.round}"
vputs "b: #{b.round}"
vputs "c: #{c.round}"
vputs "d: #{d.round}"
vputs ""
vputs "公式"
vputs "ab×ae = 0"
vputs "ab×(ac + cd*t) = 0"
vputs "(ab × ac) + (ab × cd*t) = 0"
vputs "ab × cd*t = -ab × ac"
vputs "t = -ab×ac / ab×cd"
vputs "t = ab×ac / cd×ab = #{t.round(2)}"
vputs ""
vputs "青 = cの垂線 = abの正規化×ac = #{c_length.round}"
vputs "赤 = dの垂線 = cd×abの正規化 = #{d_length.round}"
vputs "青 / 赤 = #{(c_length / d_length).round(2)}"
vector_draw(a, b, "a", "b")
vector_draw(c, d, "c", "d")
if @perp == 1
line_draw(c - ab.perp, c + ab.perp)
line_draw(d - ab.perp, d + ab.perp)
n = -ab.perp.normalize
vputs ""
vputs "内積を使う場合"
vputs "青 = cの垂線 = ca・abの法線の正規化 = #{ca.dot(n).round}"
vputs "赤 = dの垂線 = cd・abの法線の正規化 = #{cd.dot(n).round}"
end
if @mode == 0
end
if @mode == 1
line_draw(a, c)
line_draw(a - ab, b + ab)
bold_line_draw(c, c - (ab.perp.normalize * ab.normalize_or_zero.cross(ac)), color: Gosu::Color::BLUE)
bold_line_draw(d, d - (ab.perp.normalize * ab.normalize_or_zero.cross(cd)), color: Gosu::Color::RED)
line_draw(c, c + cd.project_onto(ab))
point_draw(c.lerp(d, t))
arrow_head(c, e, "e")
end
end
show
end
-
https://hooktail.maxwell.jp/bbslog/13965.html#header にて専門家に質問されている方がいたが回答を見てもよくわからなかった ↩︎
Discussion