振り子のシミュレーション
考え方

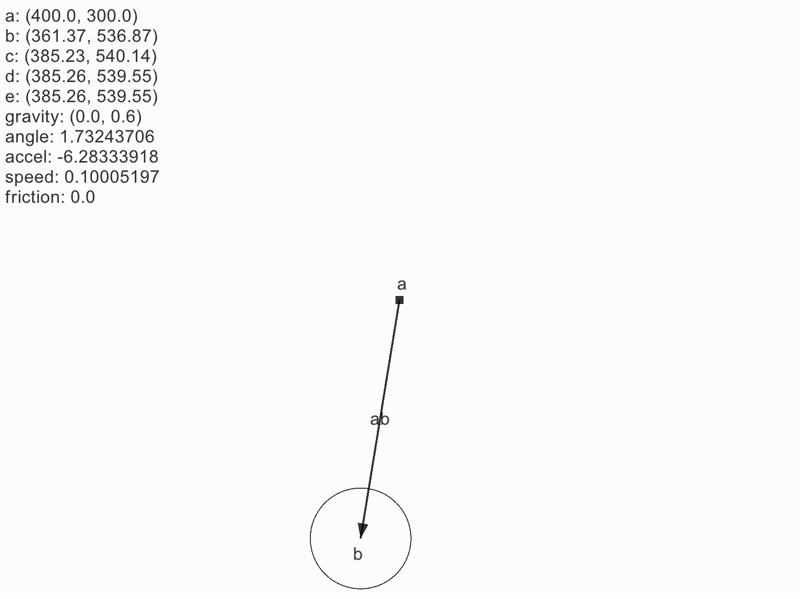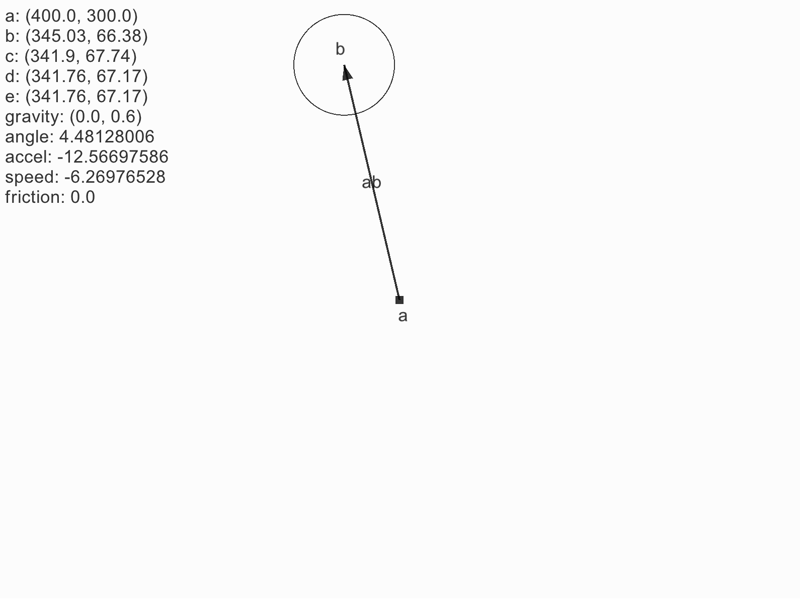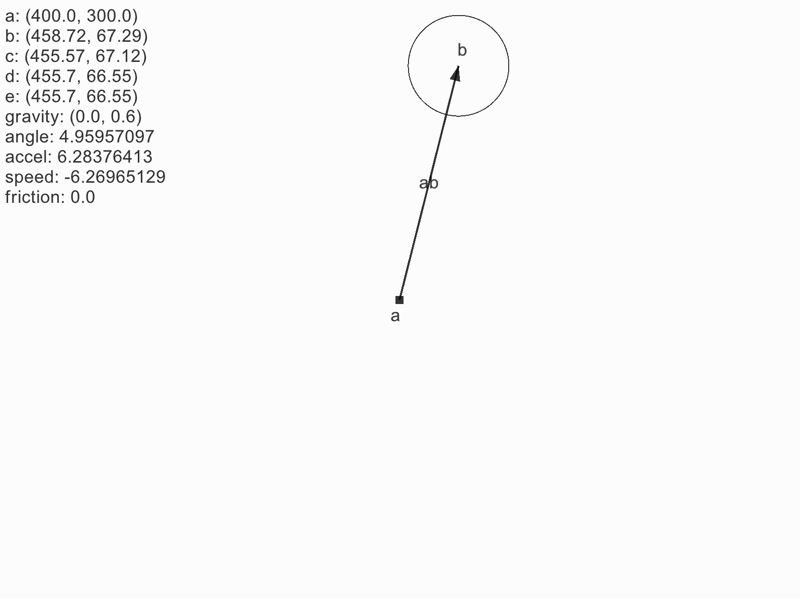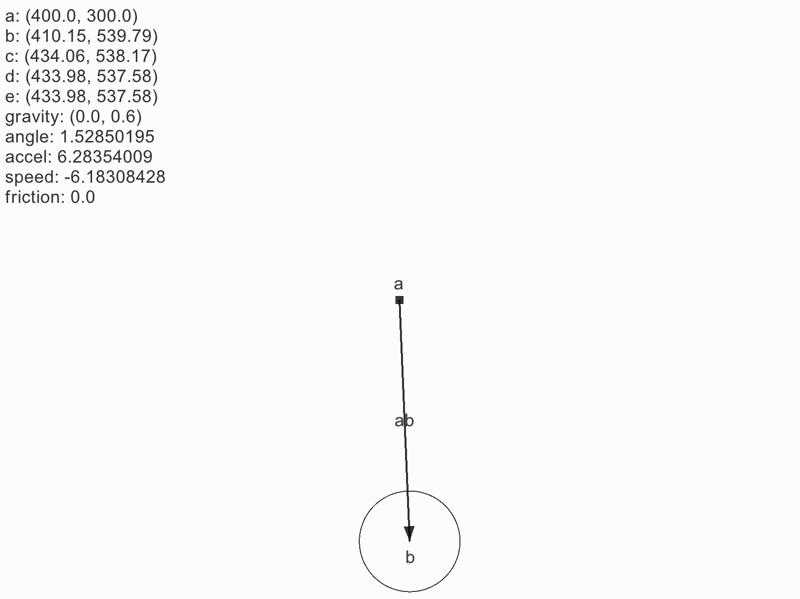
- b → c → d をイメージする
- ベクトル ab と ad の角度差を加速度とする
加速度の求め方
a = V[320.0, 60.0]
b = V[480.0, 180.0]
angle = (b - a).angle # => 0.6435011087932844
angle = a.angle_to_point(b) # => 0.6435011087932844
length = (b - a).length # => 200.0
length = a.distance_to(b) # => 200.0
シミュレータではおもり b の位置を動かせるようにしているため、最初に b から方向と糸の長さを出している。普通は方向と長さが先にあって、そこからおもりの位置を求める。
gravity = V[0.0, 200.0]
velocity = 0.0
ab の法線の正規化を用意しておく。
ab = b - a # => (160.0, 120.0)
n = ab.perp.normalize # => (-0.6, 0.8)
おもりの位置から重力を足した位置 c を求める。
c = b + gravity # => (480.0, 380.0)
そこからベクトル bc を求める。
bc = c - b # => (0.0, 200.0)
少し整理すると bc は単に重力のことだった。
bc = b + gravity - b # => (0.0, 200.0)
bc = gravity # => (0.0, 200.0)
次に bd を求める。bc が斜辺で n を地面としたとき内積で正射影 bd が求まる。
bd = n * bc.dot(n) # => (-96.0, 128.0)
bd = bc.project_onto_normalized(n) # => (-96.0, 128.0)
位置ベクトル d を求める。
d = b + bd # => (384.0, 308.0)
新しい紐のベクトル ad を求める。
ad = d - a # => (64.0, 248.0)
この辺も整理すると、
ad = ab + bc.project_onto_normalized(n) # => (64.0, 248.0)
となる。そして、新しい角度と今の角度の差が加速度になる。
accel = ad.angle - angle # => 0.6747409422235527
新しいおもりの位置を求める
ae = ad.normalize * length # => (49.97560380435394, 193.65546474187153)
ae = V.from_angle(ad.angle) * length # => (49.97560380435393, 193.65546474187153)
ae = V.from_angle(ab.angle + accel) * length # => (49.97560380435393, 193.65546474187153)
o = V.from_angle(accel)
ae = V[ab.x * o.x - ab.y * o.y, ab.y * o.x + ab.x * o.y] # => (49.97560380435392, 193.65546474187153)
ae = ab.rotate(accel) # => (49.97560380435392, 193.65546474187153)
どの方法でも ae が求まるので a を足せば新しいおもりの位置 e が求まる。
e = a + ae # => (369.9756038043539, 253.65546474187153)
ただ、この手順で求まった e で b を更新しても6時の方向を目標に減速するだけで揺れない。
揺らす
揺らすには毎フレーム、加速度を速度に足していく。
velocity += accel
angle += velocity
こうすると真下を過ぎたとき accel は符号が反転し velocity は徐々に減速・加速を繰り返すようになる。
続いて新しいおもりの位置を angle から求める。
b = a + V.from_angle(angle) * length # => (369.9756038043539, 253.65546474187153)
計算方法まとめ
a = V[320.0, 60.0] # => (320.0, 60.0)
b = V[480.0, 180.0] # => (480.0, 180.0)
angle = a.angle_to_point(b) # => 0.6435011087932844
length = a.distance_to(b) # => 200.0
gravity = V[0.0, 200.0] # => (0.0, 200.0)
velocity = 0.0 # => 0.0
ab = b - a # => (160.0, 120.0)
ad = ab + gravity.project_onto(ab.perp) # => (64.0, 248.0)
accel = ad.angle - angle # => 0.6747409422235527
velocity += accel # => 0.6747409422235527
angle += velocity # => 1.3182420510168371
b = a + V.from_angle(angle) * length # => (369.9756038043539, 253.65546474187153)
応用: 徐々に勢いをなくす
damping = 0.99995
velocity *= damping # => 0.6747072051764416
速度ベクトルに減退率を掛けていくと収束する。
応用: メトロノーム
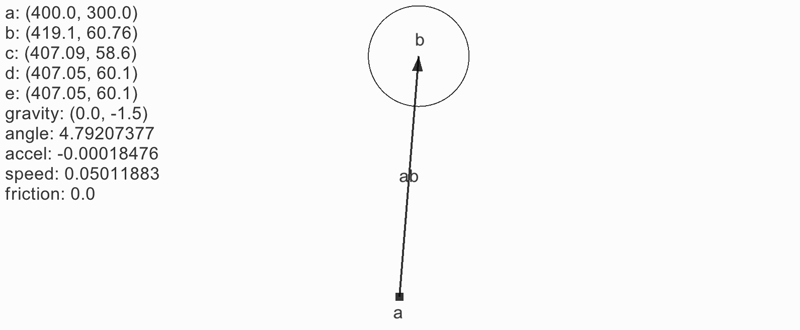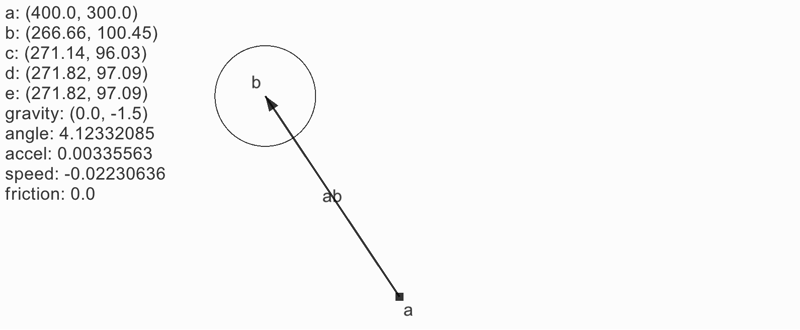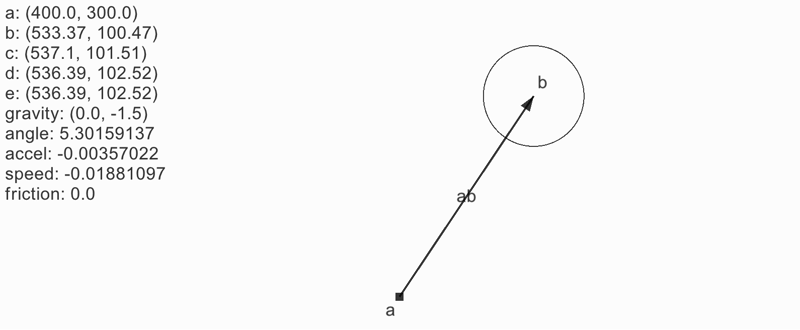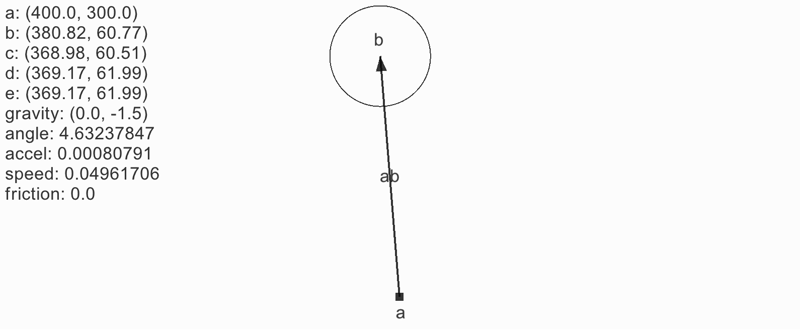
重力を反転しただけ。これでメトロノームになる。
妥協: 擬似的な振り子
counter ||= 0
angle = Math.sin((counter / 60.0 * 0.8).turn_to_rad) # => 0.0
b = a + V.from_angle(270.deg_to_rad + angle) * length # => (319.99999999999994, -140.0)
counter += 1
メトロノームのように「規則的」かつ「絶対に一周しない」場合は単に角度を sin カーブで揺らす方法もある。振り子のように見せかけるだけの方が計算量も少なくコードも簡潔になる。
疑問: ベクトル ad のかわりに ac を使うとどうなる?
図を見ていると ad の代わりに ac を使っても加速度として使えそうに思えてくる。

そこで実際に ac に置き換えてみると動いた。ただし、それは紐の長さに対して重力がとても小さい場合に限ってたまたま動いているだけだった。重力をもっと強くし、おもりが上にある状態にしてみると不自然な構図が現れる。

本来 d のあたりにあるべき新しいおもりが反対側に来ている。元のおもりを12時のあたりに持ってくると、新しいおもりは6時の方向に移動する。元のおもりが12時にあるとき、重力の影響は 0 であるべきにもかかわらず、半周分もの運動エネルギーが生まれるのはおかしい。したがって ad のかわりに ac を使うことはできない。
コード
class App < Base
def initialize
super
preset1
@mode = 0
@mode2 = 0
# preset5
# @mode2 = 1
end
def preset1
a = window_wh * V[0.4, 0.1] # => (320.0, 60.0)
b = window_wh * V[0.6, 0.3] # => (480.0, 180.0)
@points = [a, b]
@velocity = 0.0
@radius = 100
@gravity = V[0, 200.0]
@damping = 1.0
angle_update
end
def preset2
a = window_wh * V[0.500, 0.5]
b = window_wh * V[0.500, 0.1]
@points = [a, b]
@velocity = 0.001.turn_to_rad
@radius = 50
@gravity = V[0.0, 0.6]
@damping = 1.0
angle_update
end
def preset3
a = window_wh * V[0.500, 0.5]
b = window_wh * V[0.500, 0.1]
@points = [a, b]
@velocity = 0.0015.turn_to_rad
@radius = 50
@gravity = V[0.0, 0.7]
@damping = 0.99995
angle_update
end
def preset4
a = window_wh * V[0.500, 0.5]
b = window_wh * V[0.500, 0.1]
@points = [a, b]
@velocity = 0.008.turn_to_rad
@radius = 50
@gravity = V[0.0, -1.5]
@damping = 1.0
angle_update
end
# @mode2 = 1 としたときおかしいのがわかる
def preset5
a = window_wh * V[0.40, 0.5] # =>
b = window_wh * V[0.50, 0.2] # =>
@points = [a, b]
@velocity = 0.0
@radius = 100
@gravity = V[0, 300.0]
@damping = 1.0
angle_update
end
def angle_update
a, b = @points
@angle = a.angle_to_point(b)
end
def button_down(id)
super
case id
when Gosu::KB_1
preset1
when Gosu::KB_2
preset2
when Gosu::KB_3
preset3
when Gosu::KB_4
preset4
when Gosu::KB_5
preset5
when Gosu::KB_Z
@mode = @mode.next.modulo(2)
angle_update
when Gosu::KB_X
@mode2 = @mode2.next.modulo(2)
when Gosu::KB_0
@velocity = 0.0
when Gosu::KB_C
@gravity -= V[0, 0.1]
when Gosu::KB_V
@gravity += V[0, 0.1]
when Gosu::KB_B
@damping += -0.01
when Gosu::KB_N
@damping += 0.01
end
end
def draw
super
a, b = @points
ab = b - a
n = ab.perp.normalize
length = ab.length
c = b + @gravity
bc = c - b
bd = bc.project_onto_normalized(n)
d = b + bd
ad = d - a
if @mode2 == 0
accel = ab.angle_to(ad)
accel = ad.angle - @angle
else
# ab ac の差を加速度とする場合
ac = c - a
accel = ab.angle_to(ac)
end
ae = ab.rotate(accel)
# ae = V.from_angle(ab.angle + accel) * length
e = a + ae
if @mode == 1
@velocity += accel
@velocity *= @damping
@angle += @velocity
b = a + V.from_angle(@angle) * length
@points = [a, b]
# 擬似的な振り子
if false
@counter ||= 0
angle = Math.sin((@counter / 60.0 * 0.8).turn_to_rad)
b = a + V.from_angle(90.deg_to_rad + angle) * length # =>
@counter += 1
end
end
vputs "a: #{a.round(2)}"
vputs "b: #{b.round(2)}"
vputs "c: #{c.round(2)}"
vputs "d: #{d.round(2)}"
vputs "e: #{e.round(2)}"
vputs "gravity: #{@gravity.round(2)}"
vputs "angle: #{@angle.modulo(1.0.turn_to_rad).round(8)}"
vputs "accel: #{accel.round(8)}"
vputs "velocity: #{@velocity.round(8)}"
vputs "damping: #{@damping.round(8)}"
# 糸
vector_draw(a, b, "a", "b", name: "ab")
# 振り子
circle_draw(b, @radius)
if @mode == 0
# 法線
line_draw(b, b + n, infinity: true, color: :blue)
# 隠れベクトル -> c -> d
vector_draw(b, c, "", "c", line_width: nil, color: :blue, start_point: false)
vector_draw(c, d, "", "", line_width: nil, color: :blue, start_point: false)
arrow_head(d + V.from_angle(270.deg_to_rad), d, "d", color: :blue)
# 新しい振り子の位置
vector_draw(a, e, "", "", name: "ae", line_width: nil, color: :blue, start_point: false)
arrow_head(e + V.from_angle(0.deg_to_rad), e, "e", color: :blue)
circle_draw(e, @radius, color: :blue)
point_draw(e, color: :blue)
end
end
def point_dragged
super
angle_update
end
def window_size_default
V[800, 600]
end
show
end


Discussion