🐉

【11日目】主成分分析をやってみる【2021アドベントカレンダー】

2021/12/11に公開

機械学習

2021年1人アドベントカレンダー(機械学習)、11日目の記事になります。

テーマは主成分分析になります。

扱っているデータが回帰向けなので、主成分分析で次元削減しつつ目的変数のラベルの分布を見る、ということが出来ないのですが、cut関数でビニング処理を行いデータの分布を追えるようにしてみました。

また TSNE は高速化のため CUDA-TSNE を使っています。

主成分分析の理論については下記サイトでご確認ください。

Colab のコードはこちら

PCA による主成分分析

from sklearn.decomposition import PCA

pca = PCA(copy=True, n_components=None, whiten=False)
feature = pca.fit_transform(X_train_dropna)

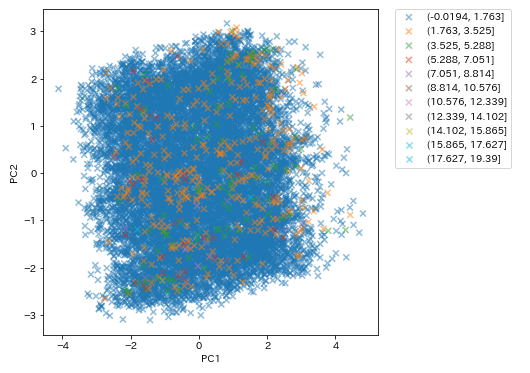
分布の可視化

bins_num = 11
labels, bins = pd.cut(y_train_dropna, bins_num, retbins=True, labels=range(bins_num))
cut, bins = pd.cut(y_train_dropna, bins_num, retbins=True)

# 第一主成分と第二主成分でプロットする
plt.figure(figsize=(6, 6))

for num in tqdm(range(bins_num)):
    plt.scatter(feature[:, 0][labels==num], feature[:, 1][labels==num], alpha=0.5,
                c=[plt.get_cmap("tab10")(x) for x in labels[labels==num]],
                label=natsorted(cut.unique())[num],
                marker="x"
                )

plt.xlabel("PC1")
plt.ylabel("PC2")
plt.legend()
plt.show()

累積寄与率

import matplotlib.ticker as ticker
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.title("累計寄与率")
plt.xlabel("主成分数")
plt.ylabel("累計寄与率")
plt.grid()
plt.show()

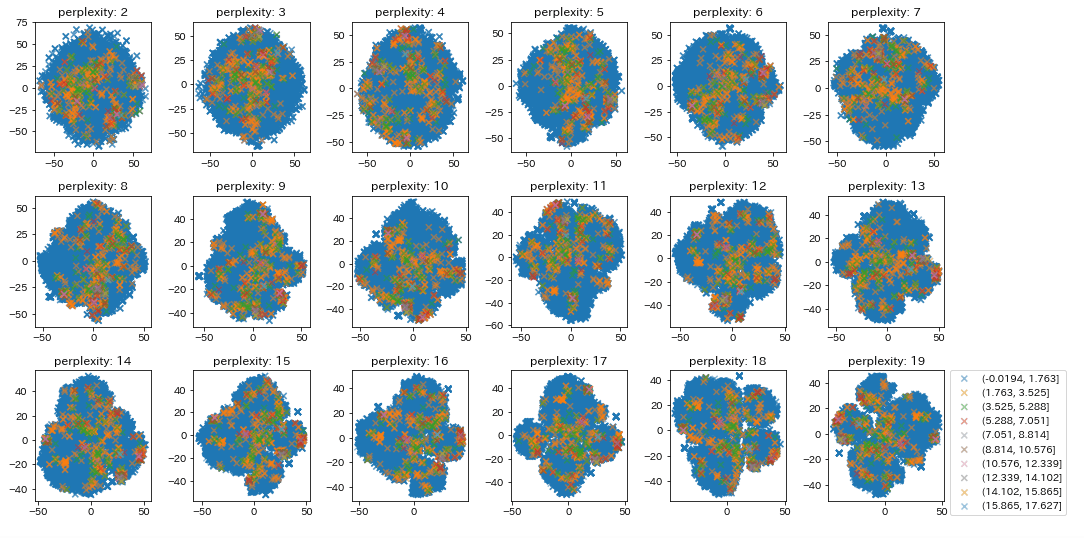
TSNE(GPU使用)

TSNE は処理に時間がかかりますので、CUDA-TSNE で GPU を使って処理を高速化します。

下記のコマンドを実行して CUDA-TSNE を Colab にインストールします。

!pip install -q condacolab
import condacolab
condacolab.install()

!wget https://anaconda.org/CannyLab/tsnecuda/2.1.0/download/linux-64/tsnecuda-2.1.0-cuda101.tar.bz2
!tar xvjf tsnecuda-2.1.0-cuda101.tar.bz2
!cp -r site-packages/* /usr/local/lib/python3.7/dist-packages/

!conda install --offline tsnecuda-2.1.0-cuda101.tar.bz2

データ分布を可視化

from tsnecuda import TSNE

fig = plt.figure(figsize=(10,15))

perplexities = 20

bins_num = 11
labels, bins = pd.cut(y_train_dropna, bins_num, retbins=True, labels=range(bins_num))
cuts, bins = pd.cut(y_train_dropna, bins_num, retbins=True)

display(pd.DataFrame(cuts.value_counts()))

for i in tqdm(range(2, perplexities)):

    plt.subplot(perplexities//4, 4, i-1)

    plt.title(f"perplexity: {i}")
    model_tsne = TSNE(n_components=2, perplexity=i)
    feature = model_tsne.fit_transform(X_train_dropna)

    # 第一主成分と第二主成分でプロットする

    for num in range(bins_num-1):
        plt.scatter(feature[:, 0][labels==num], feature[:, 1][labels==num], alpha=0.5,
                    c=[plt.get_cmap("tab10")(x) for x in labels[labels==num]],
                    label=natsorted(cuts.unique())[num],
                    marker="x"
                    )

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0)
plt.tight_layout()

ためしに主成分分析の結果を使って学習・推論を行ってみた

model_tsne = TSNE(n_components=2, perplexity=18)
feature = model_tsne.fit_transform(X_train_dropna)

y_train_dropna = y_train_dropna.reset_index(drop=True)

kf = KFold(n_splits=5)

groups = feature[:, 0]

params = {
          'task': 'train',              # タスクを訓練に設定
          'boosting_type': 'gbdt',      # GBDTを指定
          'objective': 'regression',    # 多クラス分類を指定
          'metric': 'rmse',  # 多クラス分類の損失（誤差）
          'learning_rate': 0.1,         # 学習率
          'seed': SEED                   # シード値
          }

best_params, history = {}, []

cv_result = []

for fold, (train_index, test_index) in enumerate(kf.split(feature, y_train_dropna, groups)):
    X_train_kf, X_test_kf = feature[train_index], feature[test_index]
    y_train_kf, y_test_kf = y_train_dropna.iloc[train_index], y_train_dropna.iloc[test_index]

    # 学習、推論
    lgb_train = lgb.Dataset(X_train_kf, y_train_kf)
    lgb_test = lgb.Dataset(X_test_kf, y_test_kf, reference=lgb_train)

    lgb_results = {}                                    # 学習の履歴を入れる入物

    model = lgb.train(
                    params,                    # ハイパーパラメータをセット
                    lgb_train,              # 訓練データを訓練用にセット
                    valid_sets=[lgb_train, lgb_test], # 訓練データとテストデータをセット
                    valid_names=['Train', 'Test'],    # データセットの名前をそれぞれ設定
                    num_boost_round=100,              # 計算回数
                    early_stopping_rounds=50,         # アーリーストッピング設定
                    evals_result=lgb_results,
                    verbose_eval=-1,                  # ログを最後の1つだけ表示
                    )  
    
    best_params = model.params

   # 損失推移を表示
    loss_train = lgb_results['Train']['rmse']
    loss_test = lgb_results['Test']['rmse']   
    
    fig = plt.figure()
    
    plt.xlabel('Iteration')
    plt.ylabel('logloss')

    plt.title(f"fold:{fold}")
    plt.plot(loss_train, label='train loss')
    plt.plot(loss_test, label='test loss')
    
    plt.legend()
    plt.show()

    # 推論
    y_pred = model.predict(X_test_kf, num_iteration=model.best_iteration)

    # 評価
    rmse = mean_squared_error(y_test_kf, y_pred, squared=False)
    cv_result.append(rmse)

print("RMSE:", np.mean(cv_result))

出力:
RMSE: 0.6997489550915671

Optuna によるハイパラ調整の RMSE は 0.177 だったので、学習データとして使うにはむいていないようですね。

11日目は以上になります、最後までお読みいただきありがとうございました。