Zenn
🕊️

CpawCTF Level3 Writeup

2024/07/07に公開
tech
Security
CTF
writeup
CpawCTF
tech

はじめに

サイト

https://ctf.cpaw.site/index.php

環境

  • macOS
  • M1チップ

Q23.[Reversing]またやらかした！

問題

またprintf（）をし忘れたプログラムが見つかった。
とある暗号を解くプログラムらしい…
reversing200

回答

一応， file コマンドを通しておこう．

$ file rev200  
rev200: ELF 32-bit LSB executable, Intel 80386, version 1 (SYSV), dynamically linked, interpreter /lib/ld-linux.so.2, for GNU/Linux 2.6.24, BuildID[sha1]=e87140105d6b5c8ea9b0193380ab3b79bfdcd85b, not stripped

c 言語までリバースしてあげればいけそうやな．
じゃあ， ida64 にこのファイルを食わせてあげよう．

食わせたら， F5 を押して， c 言語までリバースする．

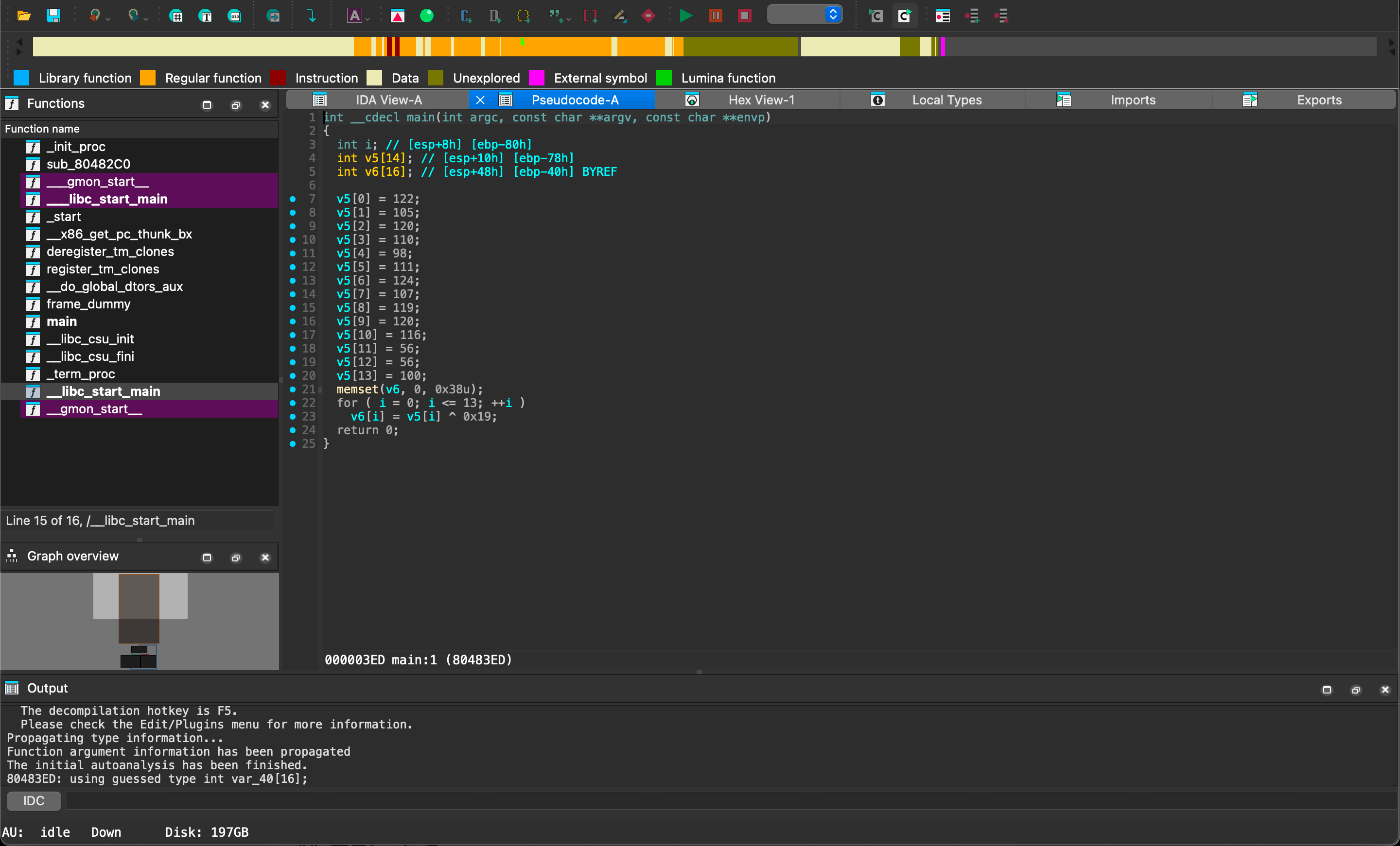
得られたソースコードに， printf するだけでなく，ライブラリも入ってないので，それも補助してあげる形で以下のようなファイルを作成する．

rev200.c
// ライブラリを持ってくる
#include <stdio.h>
#include <string.h>
int __cdecl main(int argc, const char **argv, const char **envp)
{
  int i;      // [esp+8h] [ebp-80h]
  int v5[14]; // [esp+10h] [ebp-78h]
  int v6[16]; // [esp+48h] [ebp-40h] BYREF

  v5[0] = 122;
  v5[1] = 105;
  v5[2] = 120;
  v5[3] = 110;
  v5[4] = 98;
  v5[5] = 111;
  v5[6] = 124;
  v5[7] = 107;
  v5[8] = 119;
  v5[9] = 120;
  v5[10] = 116;
  v5[11] = 56;
  v5[12] = 56;
  v5[13] = 100;
  memset(v6, 0, 0x38u);
  for (i = 0; i <= 13; ++i)
  { // ここの{を忘れないように
    v6[i] = v5[i] ^ 0x19;
    printf("%c", v6[i]);
  } // ここの}を忘れないように

  return 0;
}

これを作成したら， cc でコンパイルして実行してみる．

$ cc rev200.c
$ ./a.out
cpaw{vernam!!}

と言うわけで，答えの cpaw{vernam!!} が得られた．

Q24.[Web]Baby's SQLi - Stage 2-

問題

うーん，ぱろっく先生深くまで逃げ込んでたか．
そこまで難しくは無いと思うんだけども……．

えっ？何の話か分からない？
さてはStage 1をクリアしてないな．
待っているから，先にStage 1をクリアしてからもう一度来てね．

Caution: sandbox.spica.bzの80,443番ポート以外への攻撃は絶対にしないようにお願いします．

回答

[Web]Baby's SQLi - Stage 1- をもう一度解いてみましょう．

それでは，示されている https://ctf.spica.bz/baby_sql/stage2_7b20a808e61c8573461cf92b1fe63b3f/index.php にアクセスします．
パスワードのところに a' or 1=1 -- と言う文字列を入れて SQLインジェクション を試みます．

と言うわけで， cpaw{p@ll0c_1n_j@1l3:)} と言う答えが得られました．

Q26.[PPC]Remainder theorem

問題

x ≡ 32134 (mod 1584891)
x ≡ 193127 (mod 3438478)

x = ?

フラグはcpaw{xの値}です！

回答

一つ目の条件 x ≡ 32134 (mod 1584891) を満たすように， x の値を変化させて， 二つ目の条件 x ≡ 193127 (mod 3438478) をみたした時に， x を出力するプログラムを組む．

main.py
A0 = 32134
A1 = 193127

M0 = 1584891
M1 = 3438478

for i in range(M1):
    x = A0 + M0 * i

    if x % M1 == A1:
        print(x)

実行する．

$ python main.py
35430270439

問題文にある形式に合わせて， cpaw{35430270439} と言う答えが得られた．

Q29.[Crypto] Common World

問題

Cpaw君は,以下の公開鍵を用いて暗号化された暗号文Cを受け取りました．しかしCpaw君は秘密鍵を忘れてしまいました.Cpaw君のために暗号文を解読してあげましょう.

(e, N) = (11, 236934049743116267137999082243372631809789567482083918717832642810097363305512293474568071369055296264199854438630820352634325357252399203160052660683745421710174826323192475870497319105418435646820494864987787286941817224659073497212768480618387152477878449603008187097148599534206055318807657902493850180695091646575878916531742076951110529004783428260456713315007812112632429296257313525506207087475539303737022587194108436132757979273391594299137176227924904126161234005321583720836733205639052615538054399452669637400105028428545751844036229657412844469034970807562336527158965779903175305550570647732255961850364080642984562893392375273054434538280546913977098212083374336482279710348958536764229803743404325258229707314844255917497531735251105389366176228741806064378293682890877558325834873371615135474627913981994123692172918524625407966731238257519603614744577)

暗号文: 80265690974140286785447882525076768851800986505783169077080797677035805215248640465159446426193422263912423067392651719120282968933314718780685629466284745121303594495759721471318134122366715904

これは…？

フラグは以下のシンタックスです.
cpaw{復号した値}

※復号した値はそのままで良いですが，実は意味があります，余力がある人は考えてみてください.

回答

これは…？ に書かれている内容を見ると， 問題文に書かれている N が共通しており， e と C(暗号文) が異なっていた．これは， N が一致しているので， 共通モジュラス攻撃 ができる．と言うわけで，実装は ChatGPT に投げた．以下がコードである．

main.py
def extended_gcd(a, b):
    if a == 0:
        return b, 0, 1
    gcd, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return gcd, x, y


def mod_inverse(a, m):
    gcd, x, y = extended_gcd(a, m)
    if gcd != 1:
        raise ValueError("Modular inverse does not exist")
    return x % m


def common_modulus_attack(N, e, e_prime, C, C_prime):
    # Step 1: Calculate the gcd and the coefficients s and t using the extended Euclidean algorithm
    gcd, s, t = extended_gcd(e, e_prime)

    # Step 2: Ensure gcd is 1, otherwise attack is not applicable
    if gcd != 1:
        raise ValueError(
            "gcd(e, e') is not 1. Common modulus attack is not applicable."
        )

    # Step 3: Compute the message M
    if s < 0:
        C = mod_inverse(C, N)
        s = -s
    if t < 0:
        C_prime = mod_inverse(C_prime, N)
        t = -t

    # M = (C^s * C_prime^t) % N
    M = (pow(C, s, N) * pow(C_prime, t, N)) % N

    return M


# Example usage
N = 123456789123456789
e = 65537
e_prime = 17
C = 987654321987654321
C_prime = 123456789987654321

N = int(input("N ="))
e = int(input("e ="))
e_prime = int(input("e' ="))
C = int(input("C ="))
C_prime = int(input("C' ="))

# Decrypt the message
plaintext = common_modulus_attack(N, e, e_prime, C, C_prime)
print("Decrypted message:", plaintext)

と言うわけで，これを実行して，値を渡してあげると， 424311244315114354 と言う値が得られた．よって， cpaw{424311244315114354} と言う答えが得られた．
ちなみに， 424311244315114354 と言う文字列を ポリュビオス暗号 の復号にかけると， rsaiseasy と言う文字列が得られる．

おわりに

筆者について

https://mattsun-kun-portfolio.vercel.app/

Discussion