🌓
レンダラを作るためのメモその2 - ヤコビアン・半球上の立体角での積分

2025/04/17に公開
math
renderer
tech
 はじめに改めて3DCGのレンダラを作りたくなってきたので、自分なりに必要な知識を何回かに分けてメモしています。
前回は光の物理量と単位をまとめました。
https://zenn.dev/matcha_choco010/articles/2025-04-11-renderer-memo-1
今回はレンダラを作るうえで出くわす数学的な概念として次の2つを説明します。
ヤコビアン
立体角での積分
特に後者について、レンダラを作ろうとした人の中には、レンダリング方程式を導入する際に何の説明もなく半球上での「立体角での積分」というのを導入されて面食らった人も多いのではないでしょうか。
この記事は、この立体角での積分がどういうものかイメージを掴むことを目標にします。
この記事では、まず説明のための前提知識としてヤコビアンについて詳しめに具体例を使って解説します。ヤコビアンは基本的なレンダリングのプログラムを正しく組むためにも必要ですし、今回の立体角での積分の説明でも使います。
ヤコビアンについて説明した後で、次にパッと理解しにくい 「半球上の立体角での積分」イメージ を、理解しやすい他のパラメータ表示である方位角と天頂角での積分へ変数変換しその時のヤコビアン含めてどうなっているかを見ることで、どのようなものか理解することを目指します。
この記事の説明の流れとしては次のとおりです。
簡単な具体例をいくつか使ってヤコビアンとはどのようなものかについて理解を深めます。
ヤコビアンとは、変数変換の際に正しく変換前の空間での積分の値になるように辻褄合わせをする補正項であることを説明します。

「半球上の立体角での積分」が半球上で一様に積分を意味することを、方位角と天頂角への変数変換とヤコビアンから理解します。
最後におまけとして、立体角での積分を面積要素での積分に変数変換を行う方法も紹介します。
この記事では、数学的厳密性は置いておいて、考え方をなんとなく理解して論文を読んだりプログラムを書いたりするのに困らない最低限の知識を説明することを目標とします。厳密な議論は他の書籍などをあたってください。
この記事は個人的なメモとして独自で色々調べたりして書いたことも多く混ざっているのでなにか間違ってるかもしれません。

間違っているところや何か補足したほうが良いことがあれば教えていただけると嬉しいです。
それでは本文に入りましょう。

 ヤコビアンモンテカルロレンダリングの技術論文などを読んでいるとよく ヤコビアン（Jacobian） というものに出会います。ヤコビアンはよく|J|という記号で表したりします。また、論文を読む場合でなくても、例えばHDRI画像からのサンプリングだったり、面光源上のサンプリングだったりといった基本的なライティングのプログラムを書くうえでもヤコビアンの知識は必要になってきます。
まずは最初にヤコビアンが出てくる最小の例として、高校数学の積分の置換積分による変数変換の例から考えてみましょう。

 高校数学での置換積分高校数学で出てくる置換積分は、変数変換を使って積分を計算する方法です。
例えば、次のような積分を考えます。

\int_0^1 \sqrt{1 - x^2} dx
この被積分関数y = \sqrt{1 - x^2}はグラフにすると次のようになります。
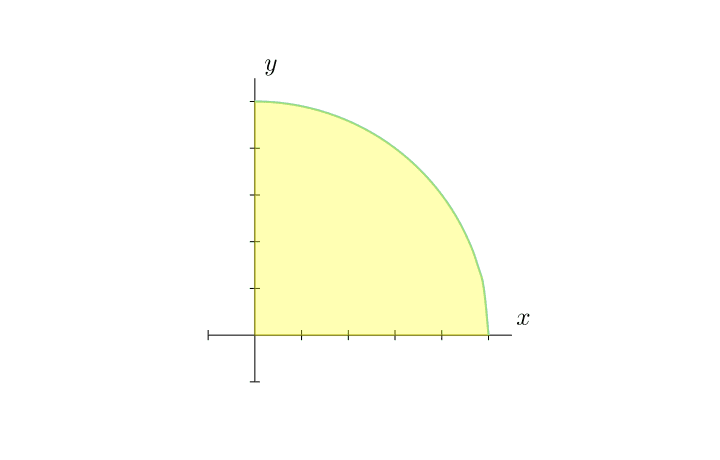
今回積分で求める面積は、半径1の円の第1象限に対応しており、y = \sqrt{1 - x^2}、x^2 + y^2 = 1という円の右上の部分を表しています。

この積分はちょうど円の第一象限の部分の面積を求めるような形になっていますね。
この面積を求めるために、変数変換を使って計算してみましょう。
一般にf(x)の積分をx = g(t)と置換すると、変数変換自体は次のように表されます。

\int f(x) dx = \int f(g(t)) \frac{dx}{dt} dt
この式自体は合成関数の微分の公式などから導けます[1]。
今回の場合はx = \sin(t)と置換すると上手いこと計算ができます。
x = \sin(t)をtで微分すると\frac{dx}{dt}は次のようになります。

\frac{dx}{dt} = \cos(t)
また、x = \sin(t)のとき、x = 0のときはt = 0、x = 1のときはt = \frac{\pi}{2}となります。

ここで、0 < t < \frac{\pi}{2}の範囲ではx = \sin(t)は単調増加なのでそのまま積分範囲として考えられますね。
このとき、積分は次のように書き換えられます。

\int_0^1 \sqrt{1 - x^2} dx = \int_0^{\frac{\pi}{2}} \sqrt{1 - \sin^2(t)} \cdot \cos(t) dt = \int_0^{\frac{\pi}{2}} \cos^2(t) dt
さらに倍角の公式を逆に使って\cos^2(t)を\cos(2t)で表すと：

= \int_0^{\frac{\pi}{2}} \frac{1 + \cos(2t)}{2} dt
= \left[ \frac{t}{2} + \frac{\sin(2t)}{4} \right]_0^{\frac{\pi}{2}}
= \frac{\pi}{4}
となって、求めたい面積は\frac{\pi}{4}となります。

これは半径1の円の面積の1/4として完璧ですね。
この計算で登場した\frac{dx}{dt} = \cos(t)の部分は実は多変数で一般化されるヤコビアンと呼ばれるものの1変数版に相当します。

 変数のスケーリング高校数学では置換積分や変数変換を、ただの数式の上での置き換えとしてのみ理解して、その意味については考えないかもしれません。変数変換は適当に計算が楽になる変数に置き換えて楽をするもの、というだけの認識で済ませることも多いでしょう。
しかし、実はこの変数変換の際の補正項のヤコビアンは座標を変えたときのスケーリングを考えるうえで非常に重要な役割を果たします。
1変数の場合、この \frac{dx}{dt} は変数を変えたときの 「横軸のスケールの変化」 を表しており、積分区間の長さがどう変わるかを補正しています。
今回の例でのスケーリングの役割を図を使って視覚的に説明してみましょう。
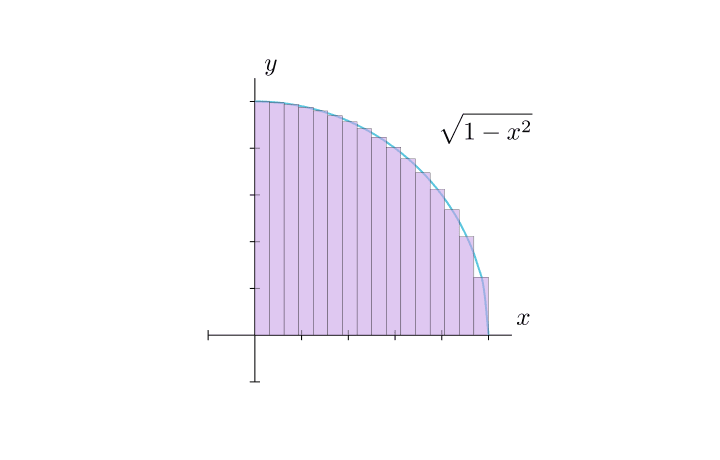
今回の積分は\sqrt{1 - x^2}のグラフを[0, 1]の区間で積分することになります。

ここで積分を区分求積のように細い短冊の足し合わせとして理解してみましょう。

今回の積分は次の図のようになります。
さて、ここでヤコビアンを掛けなかった場合の変数変換をしたものはどうなるか見てみましょう。

つまり[0, \frac{\pi}{2}]での\sqrt{1 - \sin^2(t)}の下の面積を求めることになります。

これも同様に短冊状の足し合わせとして理解すると次のようになります。
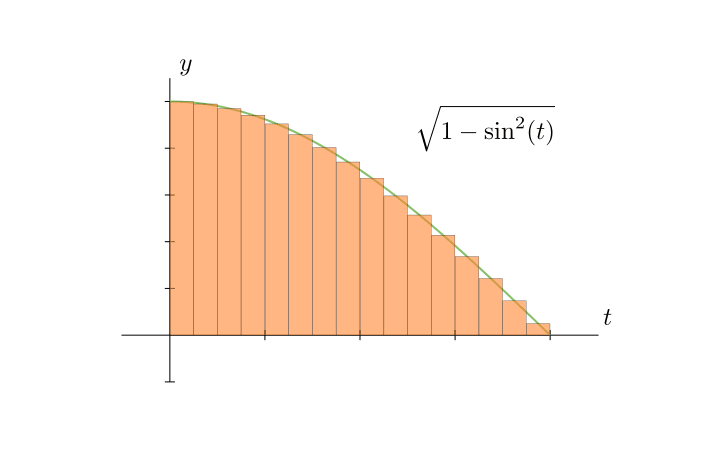
さて、この図を見れば分かる通り、2つ目の図は円の面積ではなくなっていますね。

tが\frac{\pi}{2}に近づけば近づくほど円の下を横に間延びさせたような図形になっています。
ここで、短冊の横軸の長さに\frac{dx}{dt} = cos(t)を掛けてあげた様子をアニメーションで図示してみます。
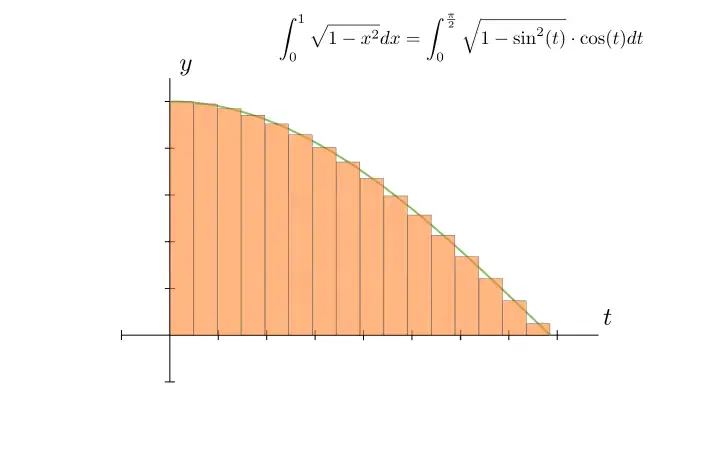
短冊の横の長さが\frac{dx}{dt}=\cos(t)でスケーリングされて右に行くほど細長い短冊になることで、全体としては円の面積に近くなりました。このように x = \sin(t)で変数変換した際に\cos(t)のスケーリングを掛けてt上の座標が\pi/2に近づくほど短冊の横幅を細くすることで積分全体が辻褄が合っていることが視覚的にわかると思います。
このスケーリングは一様なスケーリングではなく、t軸の座標の各地点で異なるスケールの値が掛かっています。
x = \sin(t)で変数変換をすると横軸のスケールが不均一に歪んで、そのまま積分してしまうともとの変数変換前の積分の面積と面積が合わなくなっていました。そこで、ヤコビアンというスケーリング係数を掛けて、変数変換後の世界で考えても正しい面積になるように調整をしていたということになります。
この調整こそが、置換積分で微分（\frac{dx}{dt}）が登場する理由となっています。各地点でのスケーリングの割合は各tでの微小長さと対応するxの微小長さの比になるのでちょうどxをtで微分したことに相当します。ただ計算を楽にするために数式をこねくり回しているものとして置換積分を理解するのではなく、視覚的なスケーリングのイメージももっておくとこの先の話が理解しやすいです。
重要なことなので改めて強調すると、変数変換後のt軸の各位置での微小幅は、対応する変換前のx軸で考えると微小幅に拡大率であるヤコビアンの\cos(t)を掛けたものになっています。
そのため、変数変換前の積分を、変数変換後の歪んだ軸での積分で求めたい場合、この各tでの拡大率（ヤコビアン）を掛けてスケーリングを調整したうえで積分をしてやる必要があるということです。
これは、ヤコビアンが変数変換の際に、正しく変数変換前の軸での積分の値になるように辻褄合わせをする補正項であるということになりますね。
上記の例は1変数関数でx軸の長さでのスケーリングでしたが、多変数になったときには、「面積」や「体積」のスケーリングに対応する値が必要になります。
ということで次に多変数関数でのヤコビアンを考えていきましょう。

 多変数関数でのヤコビアンまずは2変数でのヤコビアンの具体例を2つ見て行きます。

その後で一般の多変数の場合のヤコビアンも紹介だけします。
これらの例で、変数変換とその際に現れるヤコビアンのスケーリングのイメージを掴んでいきましょう。

 2変数関数の例2変数関数でヤコビアンを考える例題を2つ用意しました。

順に見ていきましょう。
線形変換による単純なスケーリングと回転変数変換

\begin{cases}
x=u+2v\\
y=-u+3v
\end{cases}
によって、0 \leq u \leq 2, 0 \leq v \leq 2で定義されるuv座標での正方形（面積4）の領域が、xy平面でどのような領域に移るかを調べ、その面積を求めてみましょう。
最終的に求めたい面積はxy座標系での面積になります。

まずは単純にxy座標系でどういう形になるかを考えてみましょう。
uv座標系で一辺の長さが2の正方形になりますね。2辺を\vec{u}と\vec{v}で表すと、uv座標系で次のようなベクトルとして表されます。
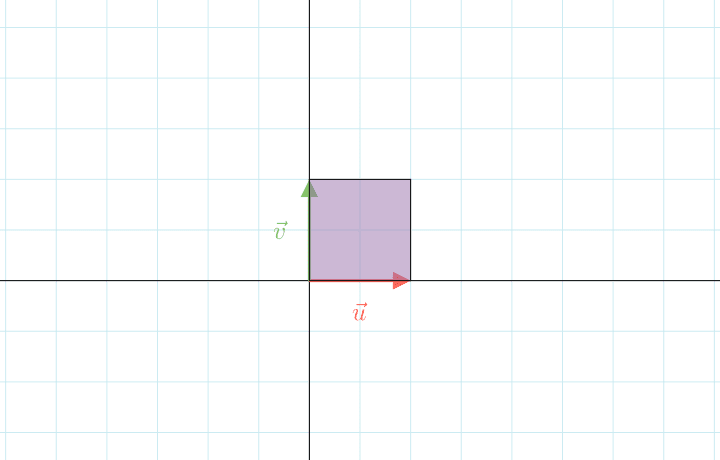
しかしこのuv座標系での面積4の正方形というのはもとのxy座標系に対して歪んでいる状態になります。これではもとのxy座標系での面積にはなりませんね。これをどうにかしてuv座標系ではなくxy座標系で写った先での面積を求めたいわけです。
まずはヤコビアンと積分の話はおいておいて、試しにベクトルuとvをそれぞれxとyで表して考えてみましょう。

\begin{pmatrix}
x\\
y
\end{pmatrix}
=
\begin{pmatrix}
1 & 2\\
-1 & 3
\end{pmatrix}
\begin{pmatrix}
u\\
v
\end{pmatrix}
ここでuv座標系でのベクトル\vec{u}=(2, 0)は変換されて：

\vec{u_{xy}} = \begin{pmatrix}
1 & 2\\
-1 & 3
\end{pmatrix}
\begin{pmatrix}
2\\
0
\end{pmatrix}
= \begin{pmatrix}
2\\
-2
\end{pmatrix}
同様に\vec{v} = (0, 2)は次のようになります。

\vec{v_{xy}} = \begin{pmatrix}
1 & 2\\
-1 & 3
\end{pmatrix}
\begin{pmatrix}
0\\
2
\end{pmatrix}
= \begin{pmatrix}
4\\
6
\end{pmatrix}
このように\vec{u}と\vec{v}、それぞれxy座標系の成分で表すと\vec{u_{xy}} = (2, -2)、\vec{v_{xy}} = (4, 6)となります。

このxy座標系でのこのベクトルの間の平行四辺形が求めたい面積になります。
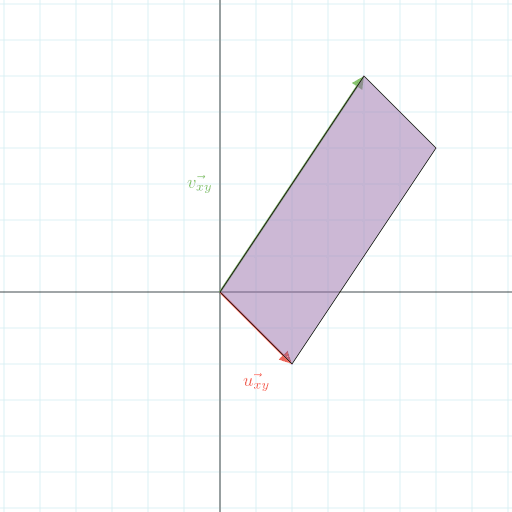
これは外積を使えば求められますね。

|\vec{u_{xy}} \times \vec{v_{xy}}| = |(2, -2) \times (4, 6)|
= |2 \cdot 6 - (-2) \cdot 4|
= 20
さて、これを本命の積分と変数変換、そしてヤコビアンを使った方法で求めてみましょう。
求めたい積分はxy座標系での面積なので、f(x, y) = 1の定数関数を使って次のように表せます。

\int \int_{D_{xy}} f(x, y) \, dx \, dy
この二重積分では実際には関数fのグラフの下の体積を求めることになりますが、f(x, y) = 1の定数関数を使っているので、積分で求めた体積は面積と一致しますね。この式は面積をちゃんと求められる式になっています。
これを変数変換を使ってuv座標系での重積分として面積を求めるにはどのような式になるかを次に示します。

\int_0^2 \int_0^2 f_{uv}(u, v) \cdot \left| det\begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{pmatrix} \right|
\, du \, dv
変数変換で変換された関数をf_{uv}(u, v)というuとvの関数として置いています。するとf_{uv}(u, v) = f(u + 2v, -u + 3v) = 1となり、こちらも値1の定数関数となります。このように変数変換をする場合はf_{uv}(u, v) = f(x(u,v), y(u,v))として、関数を新しい変数で表現し直すことになります。
ここで対象となる関数fを変数変換してf_{uv}にしただけでなく、余計な行列式の絶対値である

\left| det\begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{pmatrix} \right|
がくっついていることに気がつくと思います。
この余計な行列式の部分が、先の1変数関数で変数関数の際にxをtの関数で置き換えると出てきた\frac{dx}{dt}に相当する部分で、変数変換によるスケーリングの変更を補正する役割を持っています。xy平面上の各位置の微小面積はuv平面上の各位置の微小面積にこの行列式だけのスケーリングの補正を掛けたものになっていることを示しています。
この補正の行列式の部分はヤコビアンと呼ばれます。

このヤコビアンがどのように出てくるかは微小面積の平行四辺形のスケールから説明ができるのですが、詳細は参考文献[2]に説明を譲ります。ここでは、ヤコビアンがどういうものになっているかのイメージを掴むことにします。
ひとまず計算を進めます。ヤコビアンは今回の場合だと、

\left| det\begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{pmatrix} \right|
= \left| det\begin{pmatrix}
1 & 2 \\
-1 & 3
\end{pmatrix} \right|
= |(1 \cdot 3 - -1 \cdot 2)| = 5
ですね。
よって、求めたい面積は

\int_0^2 \int_0^2 1 \cdot 5 \, du \, dv
= 5 \int_0^2 \int_0^2 1 \, du \, dv
= 5 \cdot 2 \cdot 2 = 20
として計算できました。

こちらは先程のベクトルの外積で計算した結果ときちんと一致していますね。
このヤコビアンの行列式の絶対値を取る前の

\begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{pmatrix}
のことをヤコビ行列と言ったりします。
今回のような線形変換の場合は、線形変換の行列をAとして

\begin{pmatrix}
x \\
y
\end{pmatrix}
=
A
\begin{pmatrix}
u \\
v
\end{pmatrix}
とした際に、ヤコビ行列はAそのものでヤコビアンは|det(A)|となります。線形変換の変換行列が、そのままヤコビ行列になっていますね。そのため線形変換のヤコビアンは線形変換の変換行列の行列式の絶対値と等しくなります。
線形変換の行列式は、その線形変換はどのくらい面積が拡大されているかを表しているのでした。
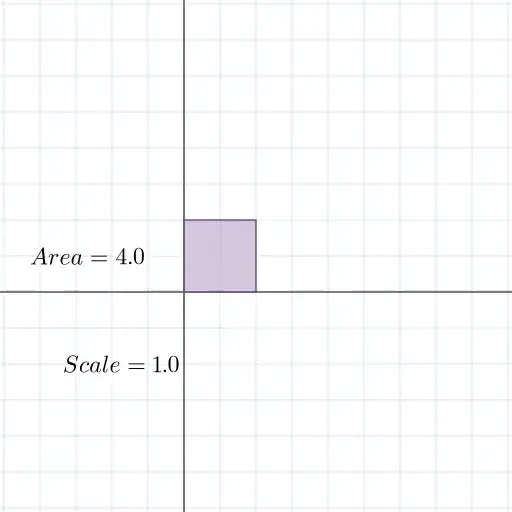
このことから、変数変換後のuv座標の各座標での微小面積は、対応する変換前のxy座標で考えると微小面積に拡大率であるヤコビアンの5を掛けたものになっています。
そのため、変数変換前の領域での積分を、変数変換後の歪んだ領域での積分で求めたい場合、この拡大率（ヤコビアン）を掛けてスケーリングを調整したうえで積分をしてやる必要があります。
これは先と同じくヤコビアンが変数変換の際に、正しく変数変換前の空間での積分の値になるように辻褄合わせをする補正項であるということになりますね。
ここで各座標での微小面積の比を考えるのは、先の1次元の例が軸の位置によって一様ではないスケーリングを考えていたように、多次元でも一様ではないスケーリングを考えたいからです。
今回は線形変換であり、空間全体で一様なスケーリングだったため、ヤコビアンはuとvの値に依存しないただの定数でした。
次はスケーリングが一様でない場合として極座標系を見てみましょう。
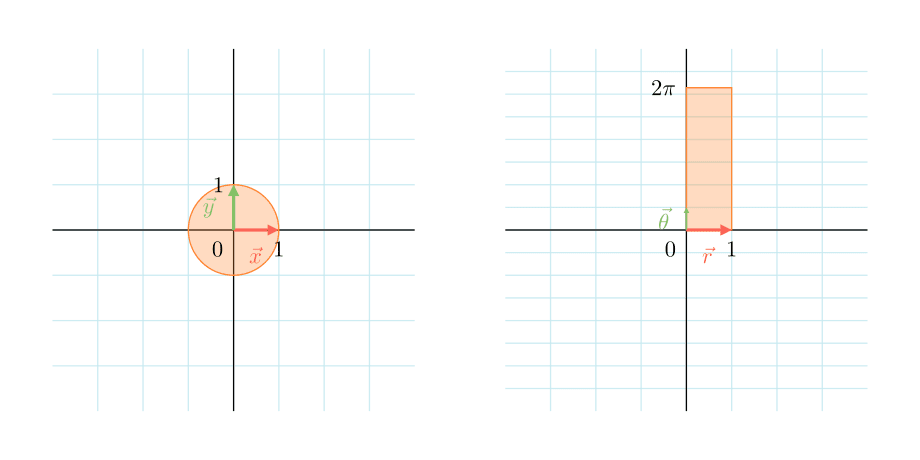
極座標による円領域の面積計算x^2 + y^2 \leq 1 という単位円内の面積を求める問題を考えます。

これは次の図のような領域での面積を求める問題ですね。
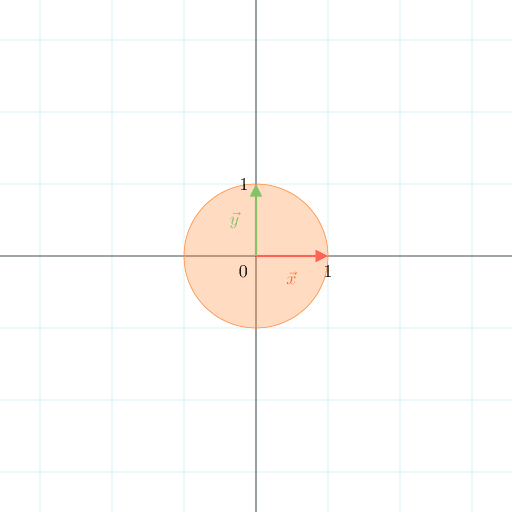
まずは変数変換せずに直交座標系で積分した値を考えます。

\int_D f(x, y) \, dx \, dy
ここで、先ほどの例と同じように積分の値が面積と一致するように、fはf(x, y) = 1の定数関数とします。
これをy軸を先に積分すると次のように書けます：

= \int_{-1}^1 \int_{-\sqrt{1 - x^2}}^{\sqrt{1 - x^2}} 1 \, dy \, dx
これを計算すると次のようになります。

= \int_{-1}^1 2\sqrt{1 - x^2} \, dx
ここで上でやった例と同じようにx = \sin(t)と置換したりして計算すれば、

= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 2\cos^2(t) \, dt
= 2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 + \cos(2t)}{2} \, dt
となり、

= 2 \left[ \frac{t}{2} + \frac{\sin(2t)}{4} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}
= 2 \left[ \frac{\pi}{4} + 0 - (-\frac{\pi}{4} + 0) \right]
= \pi
として半径1の円の面積が出てきました。
次に、極座標で変数変換を行った場合を考えてみます。

この問題では次のように極座標系に変数変換すると簡単に計算できます。

\begin{cases}
x=r \cos(\theta)\\
y=r \sin(\theta)
\end{cases}
このとき積分範囲は0 \leq r \leq 1、0 \leq \theta < 2\piとなります。

また、変数変換で変換された被積分関数をf_{r\theta}(r, \theta)と置くと、f_{r\theta}(r, \theta) = f(r\cos(\theta), r\sin(\theta)) = 1となり、値1の定数関数となります。
ヤコビアンを計算すると、

\left| det\begin{pmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}
\end{pmatrix} \right|
= \left| det\begin{pmatrix}
\cos(\theta) & -r \sin(\theta)\\
\sin(\theta) & r \cos(\theta)
\end{pmatrix} \right|

= \left| (r\cos^2(\theta) + r\sin^2(\theta)) \right|
= \left| r \cdot (\cos^2(\theta) + \sin^2(\theta)) \right|
= r
となり、ヤコビアンはrとなります。
そのため、求める面積は次のような積分で表せます。

\int_0^{2\pi} \int_0^1 f_{r\theta}(r, \theta) \cdot \left| det \begin{pmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}
\end{pmatrix} \right| \, dr \, d\theta
=
\int_0^{2\pi} \int_0^1 1 \cdot r \, dr \, d\theta
この積分を内側から順に計算すると、

= \int_0^{2\pi} \left[ \frac{r^2}{2} \right]_0^1 d\theta
= \int_0^{2\pi} \frac{1}{2} d\theta
= \frac{1}{2} \cdot 2\pi
= \pi
となり、やはり半径1の円の面積の\piが出てきました。
ここで、ヤコビアンの値がどういう解釈ができるか見てみましょう。
今回の変数変換はこのようなものでした。

\begin{cases}
x=r \cos(\theta)\\
y=r \sin(\theta)
\end{cases}
これを図示すると、下の図において右のようなrと\thetaが直行している座標系でrが定数な直線を、左のようなxy座標系での原点中心の円の円周になるように曲げた空間の変換を行っているとも見れます。
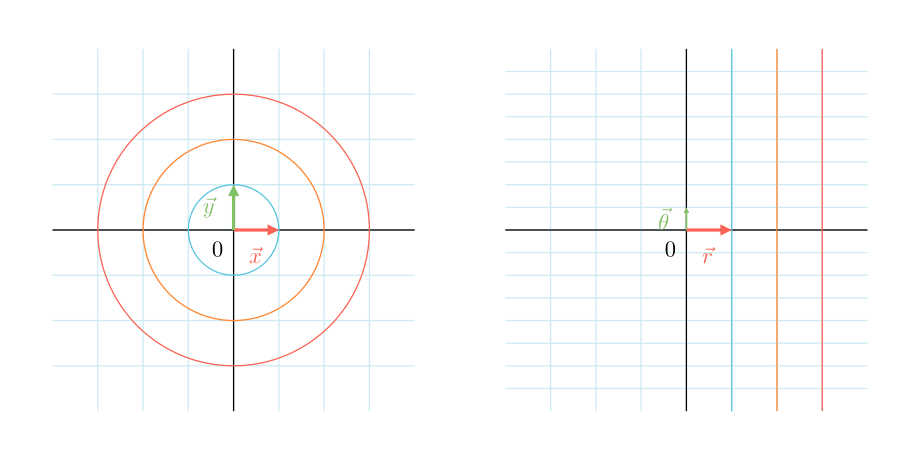
今回求めた面積をそれぞれの平面に図示すると次のようになります。
左の面積を求めるために、右の座標で計算する際にヤコビアンのrを掛けてあげることで、右の座標系での積分でも左の面積が正しく求められるようになっています。
ヤコビアンの値は微小面積のスケーリングに対応していました。今回計算したヤコビアンがrということは、変数変換後の直交座標系で原点からの距離rに比例して微小面積のスケールが大きくなっていくということですね。
これは次のような図に対応します。
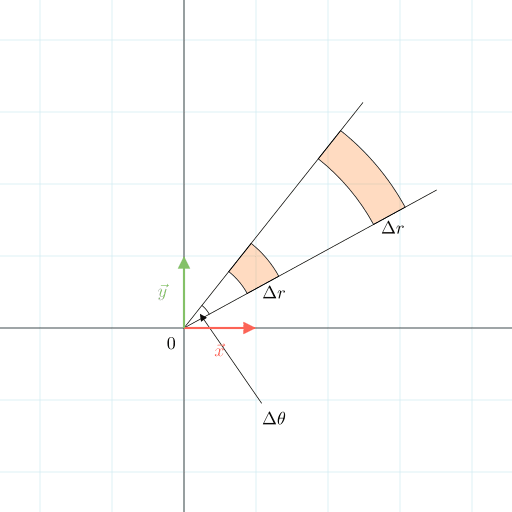
この\Delta rと\Delta\theta原点からの距離rに応じて広くなってそうなのがなんとなくわかる気がします。
rと\thetaを直行させたr\theta座標系では、どこでも一定の大きさの正方形になっていましたが、それを変数変換でxy座標系に変換すると、原点からの距離rに応じて面積が広がっていくバウムクーヘンを切ったみたいな形になっています。
これは変数変換語のr\theta座標系の各点で一様な微小面積は、変数変換前のxy座標系で表現すると座標が原点から離れるにつれて広がっているということになります。
このことをもとに考えると、r\thetaで積分するときにはこの拡大率を考慮しないと、変数変換元のxy座標での積分値と一致しないだろうことがイメージできると思います。
そして、変数変換後のr\theta座標の各位置での微小面積\Delta r \Delta \thetaは、対応する変換前のxy座標で考えると微小面積に拡大率であるヤコビアンのrを掛けたものになっています。そのため、変数変換前の領域での積分を、変数変換後の歪んだ領域での積分で求めたい場合、この拡大率（ヤコビアン）を掛けてスケーリングを調整したうえで積分をしてやる必要があります。
これも先と同じく、ヤコビアンが変数変換の際に、正しく変数変換前の空間での積分の値になるように辻褄合わせをする補正項であるということになりますね。
先の線形変換の場合ではヤコビアンはどの位置でも一定（=微小面積の拡大率はどこでも一定）でしたが、今回の極座標への変換では原点からの距離rに応じてヤコビアンの値が変わってきます。このように一般にヤコビアンによるスケーリングの補正は一様とは限りません。
ここまでいくつか具体例を見て説明してきました。
ここまでの例で、ヤコビアンについて以下の2つであると理解してください。
変数変換前と変数変換後の対応する各地点の微小な大きさのスケーリングの比になっている
変数変換元での積分を計算するために、変数変換後の領域での積分の際に掛ける補正項である

 一般的な多変数関数の場合のヤコビアン次により一般的な多変数関数でのヤコビアンの形を載せるだけ載せておきます。
より一般的な多変数関数の場合のヤコビアンは、次のように定義されます[2:1]。
n次元の変数(x_1, x_2, \cdots, x_n)からm次元の変数(z_1, z_2, \cdots, z_m)への変数変換が、関数(f_1, f_2, \cdots, f_m)によって

\begin{cases}
z_1 = f_1(x_1, x_2, \cdots, x_n)\\
z_2 = f_2(x_1, x_2, \cdots, x_n)\\
\vdots\\
z_m = f_m(x_1, x_2, \cdots, x_n)
\end{cases}
と表されるとき、ヤコビ行列は次のように定義されます。

\begin{pmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n}\\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n}
\end{pmatrix}
これは場合によっては次のように書くこともあります。

\begin{pmatrix}
\frac{\partial z_1}{\partial x_1} & \frac{\partial z_1}{\partial x_2} & \cdots & \frac{\partial z_1}{\partial x_n}\\
\frac{\partial z_2}{\partial x_1} & \frac{\partial z_2}{\partial x_2} & \cdots & \frac{\partial z_2}{\partial x_n}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial z_m}{\partial x_1} & \frac{\partial z_m}{\partial x_2} & \cdots & \frac{\partial z_m}{\partial x_n}
\end{pmatrix}
ヤコビアンはこの行列式の絶対値となります。

\left|J\right| = \left| det
\begin{pmatrix}
\frac{\partial z_1}{\partial x_1} & \frac{\partial z_1}{\partial x_2} & \cdots & \frac{\partial z_1}{\partial x_n}\\
\frac{\partial z_2}{\partial x_1} & \frac{\partial z_2}{\partial x_2} & \cdots & \frac{\partial z_2}{\partial x_n}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial z_m}{\partial x_1} & \frac{\partial z_m}{\partial x_2} & \cdots & \frac{\partial z_m}{\partial x_n}
\end{pmatrix}
\right|

 逆向きの変数変換ここで、ヤコビアンのスケーリングのイメージをより確かなものにするために、逆向きの変数変換でのヤコビアンが、もとの変数変換でのヤコビアンの逆数になっていることをみます。
ちょっと変な例になりますが、ここで極座標系でヤコビアンrを乗算しなかった場合の積分の値について考えてみましょう。定数関数1を0 \leq r \leq 1、0 \leq \theta < 2\piで積分する場合を考えます。そしてこのときのrと\thetaの値をxとyで表すような逆向きの変数変換を考えます。
まずは

\int_0^{2\pi} \int_0^1 1 \, dr \, d\theta
の積分を考えます。
まずは普通に積分を考えます。

\int_0^{2\pi} \int_D 1 \, dr \, d\theta
= \int_0^{2\pi} \left[ r \right]_0^1 d\theta
= \int_0^{2\pi} 1 \, d\theta
= 2\pi
ということで、この積分の値は2\piとなります。

これは先程の\piとはことなるので、一般的な意味での直交座標系での面積とは違う値になっていることがわかりますね。xy座標系での本来の面積を計算したい場合はヤコビアンのrをかけたうえで積分をする必要があるということでもあります。今回はほんとうの面積ではないこの値について考えていきます。
次に、次のような式で表される関係で、rと\thetaをxとyで変数変換し、ヤコビアンどうなるかを考えてみます。

\begin{cases}
r = \sqrt{x^2 + y^2}\\
\theta = \tan^{-1}(\frac{y}{x})
\end{cases}
これは、先の例での

\begin{cases}
x = r \cos(\theta)\\
y = r \sin(\theta)
\end{cases}
という変数変換の逆の変数変換を行っていることに相当します。
このヤコビアンは：

\left| det\begin{pmatrix}
\frac{\partial r}{\partial x} & \frac{\partial r}{\partial y}\\
\frac{\partial \theta}{\partial x} & \frac{\partial \theta}{\partial y}\\
\end{pmatrix} \right|
= \left| det\begin{pmatrix}
\frac{x}{\sqrt{x^2 + y^2}} & \frac{y}{\sqrt{x^2 + y^2}}\\
\frac{1}{1 + (\frac{y}{x})^2} \cdot \frac{-y}{x^2} & \frac{1}{1 + (\frac{y}{x})^2} \cdot \frac{1}{x}
\end{pmatrix} \right|
r=\sqrt{x^2 + y^2}を使って整理すると、

= \left| det\begin{pmatrix}
\frac{x}{r} & \frac{y}{r}\\
\frac{-y}{r^2} & \frac{x}{r^2}
\end{pmatrix} \right|

= \left|\frac{x}{r} \cdot \frac{x}{r^2} - \frac{y}{r} \cdot \frac{-y}{r^2} \right|

= \left| \frac{x^2 + y^2}{r^3} \right|
= \left| \frac{r^2}{r^3} \right|
= \left| \frac{1}{r} \right|
= \frac{1}{r}
ということで結構面倒でしたがヤコビアンは1/rとなりました。これは先程の直交座標のxとyを極座標のrと\thetaに変数変換した場合のヤコビアンのrのちょうど逆数になっています。
今回の変数変換が先程の変数変換の逆の変換であることを考えると、ちょうど逆数になることは不思議ではないように思います。極座標と直交座標の微小面積の比が各座標においてr:1であるということを考えればヤコビアンがrと1/rで逆の関係になっているのは自然なことですね。
今回の逆向きの変数変換でのヤコビアンは、極座標を直交座標の変数変換で表す場合に、直交座標の各点の微小面積は極座標での微小面積の1/r倍になっているということを意味しています。そのため、変数変換前の極座標での積分値を変換後の直交座標での領域の積分で計算するには、ヤコビアン1/rを掛けたうえでの積分にする必要があるということになります。
これを使って積分の式を立てると次のようになります。

\int_0^{2\pi} \int_0^1 1 \, dr \, d\theta
= \int_{-1}^1 \int_{-\sqrt{1 - x^2}}^{\sqrt{1 - x^2}} 1 \cdot \frac{1}{r} \, dy \, dx
= \int_{-1}^1 \int_{-\sqrt{1 - x^2}}^{\sqrt{1 - x^2}} \frac{1}{\sqrt{x^2 + y^2}} \, dy \, dx
もっとも残念ながらこれは直交座標系のまま積分を式変形で計算するのは難しそうです。（私は計算を断念しました）

とはいえ、直交座標系から極座標系への変数変換を行い、その際のヤコビアンの1/rを使って計算していることから、この積分値は極座標で計算したものと同じ値になることが言えるので、この値も2\piになるでしょう。
このrでの乗算無しの極座標での積分で、本来の面積ではない積分値が何なのかを次の項で説明します。

 ヤコビアンは変数変換前の積分値に合わせるための補正項さて、先のr\theta空間での定数関数1の0 \leq r \leq 1、0 \leq \theta < 2\piでの積分は結局何を考えているのでしょうか？
単位円の面積を求めるときと同じ単位円の内部の領域を積分しているようですが、面積の値\piとは異なる値が出てきていることからもわかるように、これは面積（\mathrm{m^2}）ではありませんね。なにか別の単位、もっというと長さ(\mathrm{m})と角度（\mathrm{rad}）を掛けた単位の値になってそうです。
この積分は、ちょっと不思議な設定ですが、r\theta座標系で一様に積分した場合と言えるでしょう。極座標系でrを掛けていないで積分をしたということは、極座標系で座標によらず微小面積が一様だった場合の積分の値ということになります。数学的厳密性は置いておくと、drd\thetaという微小面積が座標(r, \theta)によらず一定であるような空間で積分をしていると言ってもよいでしょう。
先程の図を使って説明します。
普通の面積を求める積分では、左のような微小面積dxdyが座標によらず一定な空間での一様な積分をしていました。その積分値を右のr\theta座標系から計算するために右から左に変数変換する際にはヤコビアンのrを掛けていました。
そして今回の積分では、右のような微小面積drd\thetaが座標によらず一様なr\theta座標系で積分をしていることになります。そしてその積分の値を左のxy座標系に変数変換して計算するためには1/rのヤコビアンを掛けて積分を計算する必要がありました。
ということで、極座標でのrのヤコビアンの掛け算をしない積分では r\theta座標系で一様に積分した場合の値を計算していることになります。
今回やったような r\theta座標系でdrd\thetaという微小面積が座標によらず一定であるような空間での積分は、xyの直交座標系のユークリッド空間での一様な積分とは別物となります。つまり、この積分値は一般的な面積には対応していない値になっているので、今回のような変数変換を行うことはあまり一般的ではないかもしれません。
とはいえ計算した積分値の物理的な意味はともかく、数学的には逆向きの変数変換で逆向きのヤコビアンを考えるというのは、ただの変数変換と思えば普通に式変形できることで別におかしな計算ではありませんね。
これらについて整理すると：
普通の面積の積分を、xy座標系で一様に積分を計算するのと、r\theta座標系に変数変換してヤコビアンrを掛けて積分を計算するのは同じ値
極座標系での定数関数の積分を、r\theta座標系で一様に積分するのと、xy座標系に変数変換してヤコビアン1/rを掛けて積分するのも同じ値
そしてこの前者と後者では別の値となり、前者が面積（\mathrm{m^2}）で、後者はそうではない別の値になっていました。
ここでわかるのは、xyの変数で積分してもヤコビアンを掛けているかどうかで物理的に違う意味になり、r\thetaの変数で積分する場合でもヤコビアンを掛けているかで物理的に違う意味になるということです。例えば、先の例では面積（\mathrm{m^2}）なのかそうではない別の積分値になるのかが変わりました。
これはどの空間をもとに積分しているかによって、最終的に出てくる積分値の物理単位が変わってくるということです。そして変数変換を使えば別の座標系での積分を、ヤコビアンを掛けて行うことで変数変換元の空間での積分に一致させられました。つまり、どの座標系でどのヤコビアンを掛けて積分をするかは積分の物理単位に関係しますね。
物理的に正しい積分の値を考えないといけない物理ベースレンダリングを行う上ではどの空間での積分を計算しているかが重要になります。そして変数変換で積分を考える座標系を変えるときにはヤコビアンが出てくるわけですから、座標系を切り替えつつ物理の単位を正しく取り扱おうとするとよくヤコビアンが出てくるということになります。これが物理ベースレンダリングを扱う論文などでヤコビアンがよく登場する理由になります。
ヤコビアンをただの変数変換の過程の計算の辻褄合わせのものと考えていれば、別にややこしいことを考えなくてもヤコビアンを使った計算はできるのですが、どの空間で積分を行うか、そのためにどのヤコビアンを掛けるかと言うのを意識すると、立体角上の積分を理解しやすくなるため、ちょっとくどいくらいに繰り返しの説明をしました。
この後すぐに説明しますが、レンダリング方程式に出てくる半球上の立体角での積分というのを考えるにあたって、このあたりの理解は大事になります。
立体角上の積分から物理単位を変えずに変数変換を考えてヤコビアンを掛けつつ別の領域での積分をするというのがレンダリングを行う上でよくあります。その立体角上の積分から変数変換を考えるときに出てくるヤコビアンがどういう意味かについては、これまでの例で変数変換元の積分になるように辻褄を合わせるためにヤコビアンを与えていることをちゃんと理解していれば飲み込めるはずです。

 立体角上での積分次は、レンダリング方程式に含まれている半球上の立体角での積分について説明していきます。
最初に半球上の立体角での積分について説明した後で、変数変換を利用して他の領域での積分をこの立体角での積分に変換する例を説明します。
そもそも立体角とはなにかについては前回の記事で言及しているので確認してください。
https://zenn.dev/matcha_choco010/articles/2025-04-11-renderer-memo-1

 単位球面上での積分レンダリング方程式とかには立体角での積分が含まれています。
レンダリング方程式はまだちゃんと説明していないですが次のようなものです。

L_o(x, \vec{\omega_o}) = L_e(x, \vec{\omega_o}) + \int_{\Omega}f_r(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i})|\vec{\omega_i} \cdot \vec{n}|d\vec{\omega_i}
\Omegaは半球上の立体角の領域です。

このレンダリング方程式では、\omega_iを\Omegaの立体角の領域全体で積分していることになります。
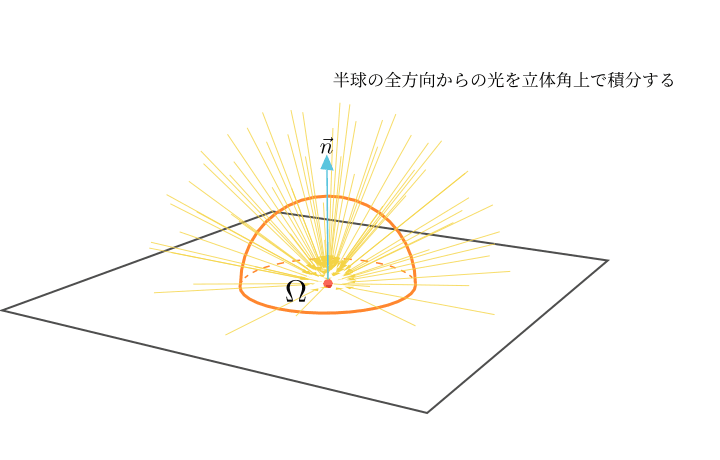
この\Omegaの範囲での積分のような立体角に関する積分を、立体角での積分とかDirectional Domainでの積分と呼ぶことがあります。
レンダリング方程式の意味はまた別の記事でまとめるとして、ここでは\int_{\Omega}f(\vec{\omega_i}) \,\, d\vec{\omega_i}の積分を見ていきます。
この式はf(\vec{\omega_i})を立体角上で一様に積分していることになります。

イメージとしては半球の全方向について\vec{\omega_i}を変化させてf(\vec{\omega_i})を重みを付けずに足し合わせていくような計算になります。
モンテカルロレンダラを作る際は、この立体角上で一様な積分を直接モンテカルロ積分で解くことになります。
この立体角上で一様な積分というのが重要で、これがこの立体角上での積分の意味になります。とはいえこれだけではイメージが湧きにくいかもしれません。この積分をよりよく理解するために、次の項で他の座標系に変数変換した場合の様子を見ていきます。
変数変換をした場合でもヤコビアンを掛けてやることで、変換前の積分を計算した場合と同じ値になるように辻褄を合わせられるのでした。今回の立体角上での積分は立体角上での積分と一致するように変数変換した他のパラメータ表示での積分を考え、そこから立体角で一様な積分とはなにかを見ていきます。
特に今回は方位角と天頂角でのパラメータ表示に変数変換した場合を見ていきます。

 方位角と天頂角のパラメータ表示方向を方位角\phiと天頂角\thetaで0 \leq \phi < 2\pi、0 \leq \theta \leq \piと考えることが出来ます。
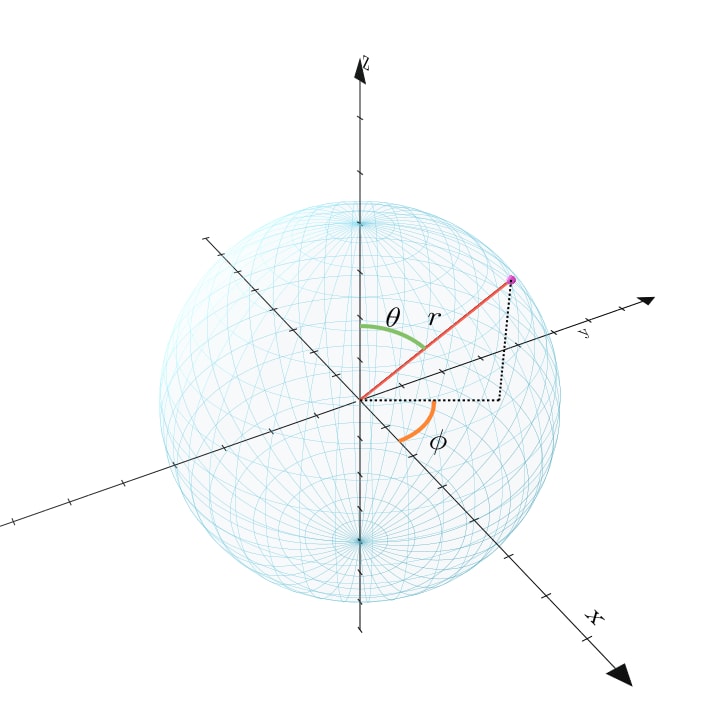
これは正距円筒図法と対応しています。
全天球を正距円筒図法で表現した画像としてHDRI画像というのがあり、これはレンダリングでもよく使われますね。
https://polyhaven.com/a/golden_gate_hills
さて、立体角での積分をこの方位角\phiと天頂角\thetaに変数変換して積分した場合を考えていきましょう。
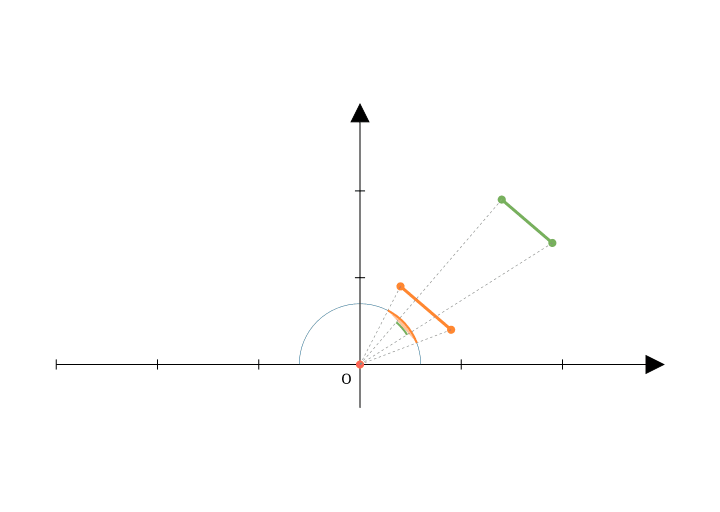
この方位角と天頂角に変数変換したときのヤコビアンを計算するためには各\phiと各\thetaにおける微小面積が、対応する立体角のどのくらいの微小大きさ（=微小立体角）になっているかの比を考えれば良いことになります。\Delta \phiと\Delta \thetaで作られる微小面積が、立体角上でどのくらいの微小立体角に当たるか、そのスケーリングを見ていきましょう。
ここで、立体角は単位球面上の面積です。ということは、単位球面に写した\Delta \phiと\Delta \thetaで作られる微小面積を考えることが微小立体角を計算することに相当します。
立体角での積分とか立体角の大きさというと角度での積分みたいなのでピンとこないですが、立体角とは要するに単位球のある領域の表面積で表されるものでした。そのため\Delta \phiと\Delta \thetaを単位球の表面に投影した表面積を考えれば、それが微小立体角を考えることに繋がり、ヤコビアンを計算できるわけです。
ということで、[\phi, \phi + \Delta \phi]と[\theta, \theta + \Delta \theta]で作られる微小立体角は、次の図のようになります。
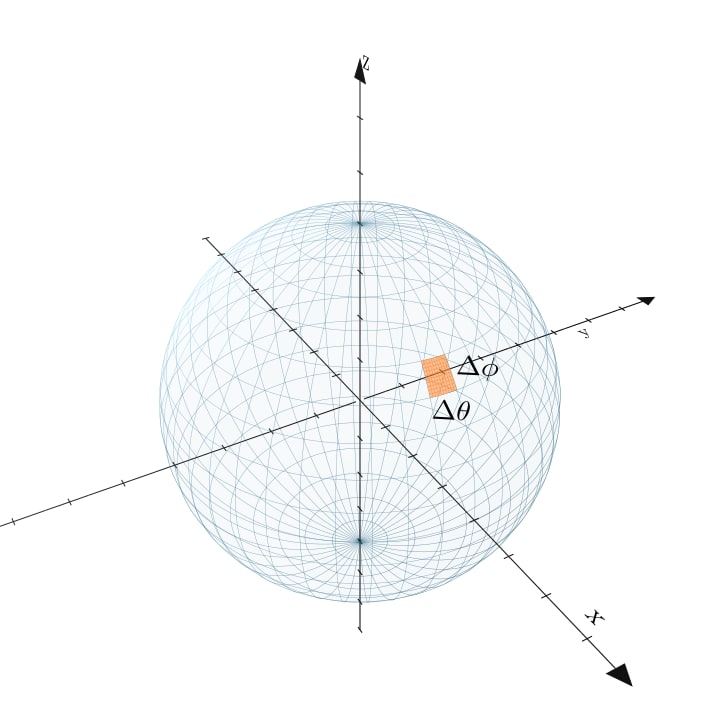
この塗りつぶされた領域の面積について、計算したいヤコビアンというのは、\Delta \phiと\Delta \thetaを0に近づけた極限での面積の比率を考えることになります。
そして、ここでは詳しく理屈は証明しませんが、\Delta \phiと\Delta \thetaを0に近づける極限においてはこの比率における高次の項は無視して一次近似で計算できるという事実があります。
この事実を使うと求める立体角上の微小大きさ（=微小立体角）と\phi \thetaの微小面積の比は、(\phi, \theta)の方向での\phiと\thetaの微小変化に対応する接ベクトルの外積の大きさで計算できます。
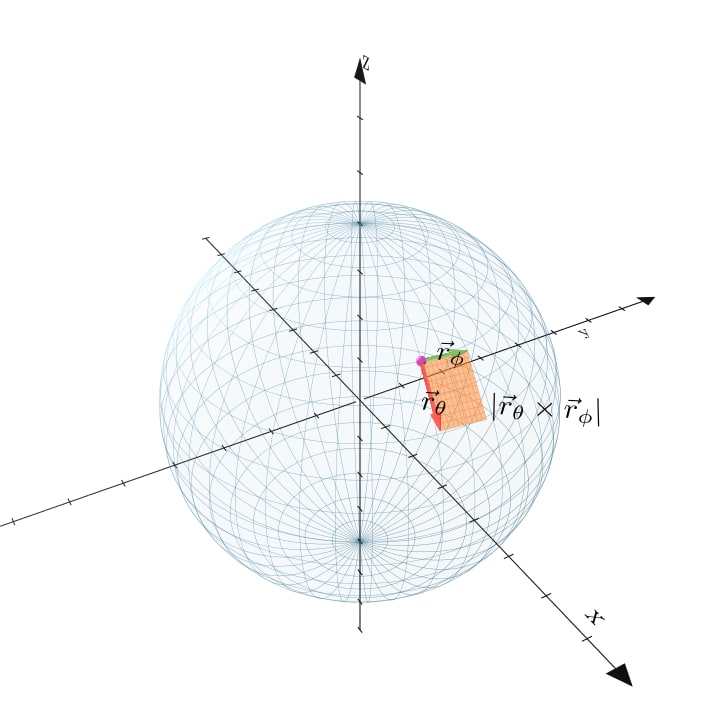
ここで、\vec{r_{\phi}}と\vec{r_{\theta}}はそれぞれ単位球場の点\vec{r}における\phiと\thetaの方向の接ベクトルです。このとき、その求める微小立体角と微小面積の比は次のように書けます。

|\vec{r_{\phi}} \times \vec{r_{\theta}}|
ここで、天頂角\thetaと方位角\phiの方向での球面上の点の座標は次のように表せます。

\begin{cases}
x = \sin(\theta) \cos(\phi)\\
y = \sin(\theta) \sin(\phi)\\
z = \cos(\theta)
\end{cases}
\vec{r} = (x, y, z)とすると、\vec{r_{\phi}}と\vec{r_{\theta}}は次のように表せます。

\vec{r_{\phi}} = \left( \frac{\partial x}{\partial \theta}, \frac{\partial y}{\partial \theta}, \frac{\partial z}{\partial \theta} \right)
= \left( -\sin(\theta) \sin(\phi), \sin(\theta) \cos(\phi), 0 \right)

\vec{r_{\theta}} = \left( \frac{\partial x}{\partial \phi}, \frac{\partial y}{\partial \phi}, \frac{\partial z}{\partial \phi} \right)
= \left( \cos(\theta) \cos(\phi), \cos(\theta) \sin(\phi), -\sin(\theta) \right)
このとき、\vec{r_{\phi}}と\vec{r_{\theta}}の外積は次のように計算できます。

\vec{r_{\phi}} \times \vec{r_{\theta}} = \left(
\begin{vmatrix}
\cos(\theta) \sin(\phi) & \sin(\theta) \cos(\phi) \\
-\sin(\theta) & 0
\end{vmatrix},
-1 \cdot \begin{vmatrix}
\cos(\theta) \cos(\phi) & -\sin(\theta) \sin(\phi) \\
-\sin(\theta) & 0
\end{vmatrix},
\begin{vmatrix}
\cos(\theta) \cos(\phi) & -\sin(\theta) \sin(\phi) \\
\cos(\theta) \sin(\phi) & \sin(\theta) \cos(\phi)
\end{vmatrix}
\right)
ここでそれぞれの成分は、
x成分：

\begin{vmatrix}
\cos(\theta) \sin(\phi) & \sin(\theta) \cos(\phi) \\
-\sin(\theta) & 0
\end{vmatrix} = sin^2(\theta) \cos(\phi)
y成分：

-1 \cdot \begin{vmatrix}
\cos(\theta) \cos(\phi) & -\sin(\theta) \sin(\phi) \\
-\sin(\theta) & 0
\end{vmatrix} = -sin^2(\theta)\sin(\phi)
z成分：

\begin{vmatrix}
\cos(\theta) \cos(\phi) & -\sin(\theta) \sin(\phi) \\
\cos(\theta) \sin(\phi) & \sin(\theta) \cos(\phi)
\end{vmatrix}

= \cos(\theta) \cos(\phi)\sin(\theta) \cos(\phi) +\sin(\theta) \sin(\phi) \cos(\theta) \sin(\phi) \\

= \cos(\theta)\sin(\theta)(\cos^2(\phi) + \sin^2(\phi)) \\

= \cos(\theta)\sin(\theta)
よって求める外積は、

\vec{r_{\theta}} \times \vec{r_{\phi}} = \left(
sin^2(\theta) \cos(\phi), -sin^2(\theta)\sin(\phi), \cos(\theta)\sin(\theta)
\right)
この外積の大きさを計算すると、

|\vec{r_{\theta}} \times \vec{r_{\phi}}| = \sqrt{(sin^2(\theta) \cos(\phi))^2 + (-sin^2(\theta)\sin(\phi))^2 + (\cos(\theta)\sin(\theta))^2}

= \sqrt{sin^4(\theta) (\cos^2(\phi) + \sin^2(\phi)) + \cos^2(\theta)\sin^2(\theta)}

= \sqrt{sin^4(\theta) + \cos^2(\theta)\sin^2(\theta)}

= \sqrt{sin^2(\theta)(sin^2(\theta) + \cos^2(\theta))}

= \sqrt{sin^2(\theta)}

= sin(\theta)
したがって、微小立体角要素d\omega_iと変数変換後の微小面積d\phi d\thetaの比は次のように表せます。

d\omega_i = |\vec{r_{\phi}} \times \vec{r_{\theta}}| \, d\phi \, d\theta
= sin(\theta) \, d\phi \, d\theta
これは、立体角の空間から方位角と天頂角の空間への変数変換を行ったときのヤコビアンが\sin(\theta)であるということになります。
ヤコビアンが\sin(\theta)ということは、変数変換した際は天頂に近づくほど小さくなる値で補正をかけていることになります。この補正をビジュアライズして理解していきましょう。
方位角天頂角空間で一様に点を取ってみます。これはHDRI画像からピクセルの値を全部拾ってくるようなものですね。
このとき、この一様な点の上側を半球に写すとどうなるかを、アニメーションで表示してみました。
図を見れば分かる通り、方位角天頂角空間で一様だった点列は、半球においては天頂ほど円周方向にぎゅっと詰まった密度の高い分布になりました。
ここで、ヤコビアンを掛けるのは天頂ほど密度が高いのでその分割り引いた補正項を掛けているとみなせます。天頂に近づくほど微小面積を小さくして積分しないと、\phi \theta座標系では天頂の方が過密になっているということですね。
そして、この様にヤコビアンが天頂ほど偏りがあるのを補正しているということを考えると、立体角での積分というのは偏りなく一様に立体角上で積分することだということが想像できると思います。
もう一つビジュアライズをしてみます。
方位角天頂角空間で一様にランダムに点を配置して、それを立体角空間に移す場合をアニメーションで表示してみました。次のアニメーションの図のように天頂からのサンプル数が多くなってしまう事がわかります。
ここで、一様乱数ではなく\sin(\theta)で重みを付けた乱数を計算すると次のようになります。
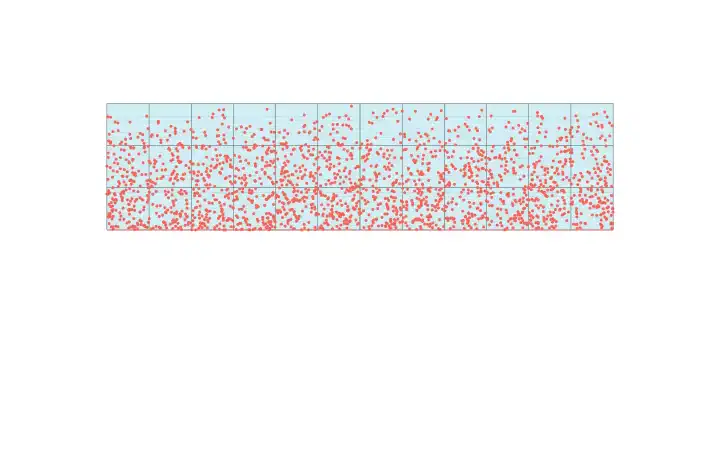
このように、\sin(\theta)で重みを付けてサンプリングした場合は、天頂の方に偏りが無くなり、立体角上で一様にサンプリングされていることがわかります。見比べてみると下の天球の方が均一に分布していることがわかりますね。
sin(θ)で重みを付けてサンプリングするコードちなみに、\sin(\theta)で重みを付けて全天球で一様になるように乱数をサンプリングするコードはざっくりと次のようになります。
def sample_hemispherical_uniform():
    u = random.random()
    v = random.random()
    phi = 2 * math.pi * v  # [0, 2pi]
    theta = math.acos(u)   # [0, pi/2]
    return phi, theta
\theta方向に\sin(\theta)の重みを付けたうえでサンプリングをするのに\arccos(u)が出てくる理由を軽く説明すると次のとおりです。
定数Cを用意して次の積分\int\int C \cdot \sin(\theta) d\theta d\thetaを考えます。

これは立体角での積分を\thetaと\thetaでの積分に変数変換したときのヤコビアンが\sin(\theta)であることを考えると、立体角上での一様な定数関数Cを立体角で積分するものになります。
ここで、突然ですがu = 1 - cos(\theta)で変数変換をしてやるとdu = \sin(\theta) d\thetaとなり、d\theta = \frac{du}{\sin(\theta)}となります。
この変数変換を考えると先の積分は、\int\int C \cdot \sin(\theta) d\theta d\theta = \int\int C du d\thetaとなります。

これでuと\thetaに対して余計な重みを付けずに一様に積分すれば元の立体角での積分になることがわかります。
つまりu = 1 - cos(\theta)の関係式の上でuが一様になるようにサンプリングすれば、\sin(\theta)の重みを付けたサンプリングと同じことになります。

これは\theta = \arccos(1 - u)でuを一様にサンプリングすれば良いことになります。

uは[0, 1]の範囲での一様サンプルなので1 - u = u'と置き換えると、\theta = \arccos(u')となります。
そのため[0, 1]区間の一様乱数uを\theta = arccos(u)に入れてサンプリングすることで、\sin(\theta)の重みを付けたサンプリングができることになります。
逆関数法との関係先程突然導入したu = 1 - \cos(\theta)ですが、これは逆関数法（Inversion Method, Inverse Transform Method）[3]で導き出せるものです。
逆関数法は累積分布関数CDFの逆関数に一様乱数を入れることで所望の分布からサンプリングした乱数を得る手法です。
[0, \pi/2]の範囲を\sin(\theta)の重みに沿ってサンプリングすることを考えます。

これは確率密度関数PDF p(\theta)がp(\theta) = \sin(\theta)であるような分布からサンプリングすることになります。[0, \pi/2]の範囲の\sin(\theta)の積分値は1なので、そのままで確率密度関数の積分が1になるような正規化がされた分布になっていると言えます。
ここで、このPDFの累積分布関数CDFをP(\theta)と置くと、P(\theta) = \int_0^{\theta} \sin(t) dt = 1 - \cos(\theta)であり、サンプリングにはこの逆関数P^{-1}(u) = \arccos(u)を使っているということになります。
逆関数法でサンプルを所望の分布から得る方法などは、また別の記事で詳しく説明したいと思います。
ということで、立体角での積分を方位角と天頂角空間に変数変換してみました。立体角での積分を、ヤコビアンの\sin(\theta)を掛けて方位角と天頂角空間で積分したものとみなせることが言えました。そこからビジュアライズを通じて、ヤコビアン\sin(\theta)を掛けた方位角天頂角での積分=立体角での積分は立体角上で一様に積分しているということがわかりました。
ちなみに、この方位角と天頂角での変数変換を行いヤコビアンを使って立体角での積分を計算する手法は、実際のレンダリングのプログラムを書くうえでも必要になります。
例えば、HDRIの画像を光源にしたレンダリングなどで、立体角空間と方位角天頂角空間の変数変換の際のヤコビアン\sin(\theta)が必要になります。ヤコビアンを使わないでHDRIをサンプルすると、天頂にサンプルが集中して、これは結果的に間違った照度を計算する原因になります。これは、物理的には「ある方向からの寄与を過大評価してしまう」ことになるためです。

 半球状に投影した面積での計算最後におまけで、もう一つ別の例としてレンダラを作るうえで必要になる別の球面上での一様な積分値の計算の方法を説明します。
面光源があって、この光源面からシェーディング点に届く光を立体角上で一様に積分して計算したいとします。このとき、計算するのは面光源の面を単位球に投影した領域で立体角での積分になります。
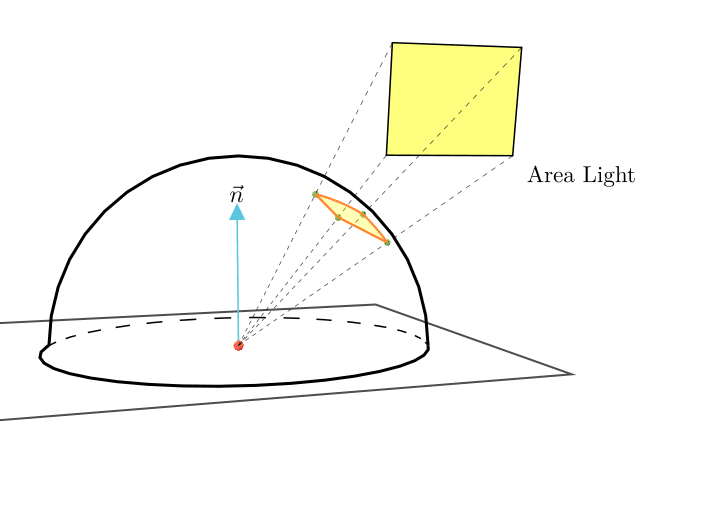
これを面光源上での積分に変数変換して面光源で積分して積分値を求める場合を考えます。
ここで立体角上での積分を計算するために、変数変換で面光源領域での積分に変換した場合のヤコビアンを考える必要があります。ヤコビアンを掛けて面光源領域で積分することで、立体角での投影領域の一様な積分と一致させられます。
これは積分領域を半球上の立体角\Omegaから光源面の面積Mに変数変換することになりますね。

図としては次のようになります。
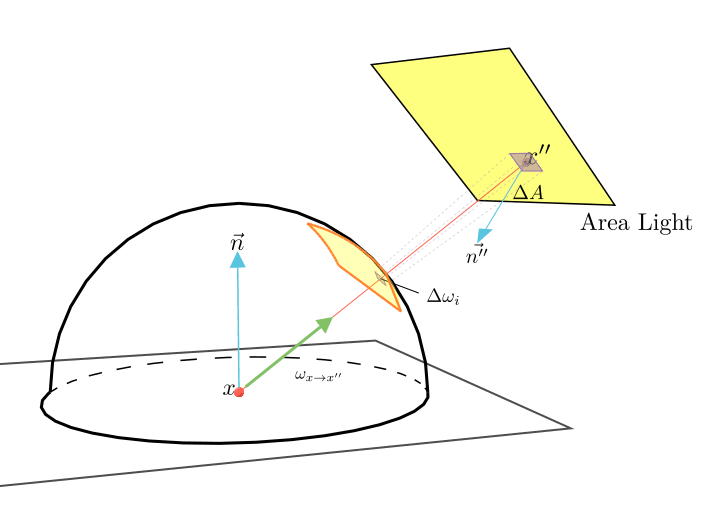
このときのヤコビアンは次のようになります。（導出は省略）

d\omega_i = \frac{|\vec{\omega_{x → x''}} \cdot \vec{n''}|}{||x - x''||^2} dA
ここで、xはシェーディング点の座標、x''は面光源上の点の座標で、||x - x''||^2はその2点間の距離です。\omega_{x → x''}はシェーディング点xから面光源上の点x''への方向ベクトル、\vec{n''}は面光源のx''での法線ベクトルです。
この式は光源面とシェーディング点が離れると、距離の逆二乗に従って減衰することを表しています。これは同じ面積がシェーディング点から離れると投影面積が小さくなることからイメージできるでしょう。
また、光源点の法線とシェーディング点から光源点への方向ベクトルの内積の絶対値も関係しています。これは、光源面がシェーディング点の方を向いていたら投影面積が大きくなって、斜めになっていたら投影面積が小さくなることからイメージがつくと思います。
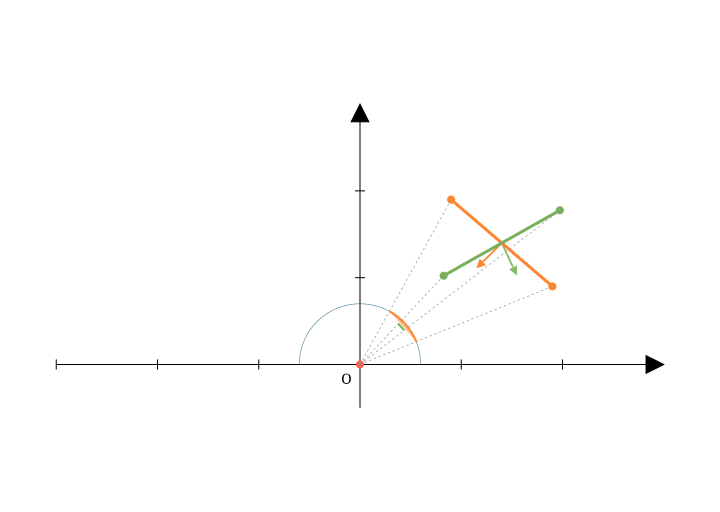
この結果として、元のレンダリング方程式は面光源上で積分をする場合は次のように書けます。

L_o(x, \vec{\omega_o}) = L_e(x, \vec{\omega_o}) + \int_M f_r(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i}) |\vec{\omega_{x → x''}} \cdot \vec{n}| \frac{|\vec{\omega_{x → x''}} \cdot \vec{n''}|}{||x - x''||^2} V(x'' ↔ x) dA
立体角の積分で定義されていたレンダリング方程式が、ヤコビアンで面光源の面領域Mでの積分になりました。ここでV(x'' ↔ x)はシェーディング点xから光源面上の点x''までの距離が遮蔽されていないかどうかを表す可視関数です。
ここで式の積分の中を後半部分をG(x↔x'')と置き換えると、次のように書けます。

L_o(x, \vec{\omega_o}) = L_e(x, \vec{\omega_o}) + \int_M f_r(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i}) G(x↔x'') dA_{(x'')}
これは3点形式のレンダリング方程式と呼んだりします[4]。
このG(x↔x'')は幾何項と呼ばれるものです。

G(x↔x'') =\frac{ |\vec{\omega_{x → x''}} \cdot \vec{n}| |\vec{\omega_{x → x''}} \cdot \vec{n''}|}{||x'' - x||^2} V(x'' ↔ x)
半球状から一様にサンプリングするのではなく、面光源の面上からサンプリングして計算する場合にはこちらの3点形式のレンダリング方程式を使うことになります。
ということで、3点形式のレンダリング方程式は、立体角での積分を面光源上での面積要素の積分に変数変換することで求まりました。
立体角での積分の理解と、そして立体角での積分を別の領域への変数変換したうえでの積分の計算というのは、レンダラを書く上でよく出てくる重要な知識になることがわかると思います。

 参考にしたサイト・書籍この記事を書くにあたって参考にした記事などを列挙しておきます。
高校レベルの置換積分について次のサイトがわかりやすかったです：

https://manabitimes.jp/math/1159
ヨビノリの動画も復習としてちょうどよいものでした：

https://www.youtube.com/watch?v=qpDZS1bzt-E

https://www.youtube.com/watch?v=Iu8jVdkiKTc
重積分の変数変換とヤコビアンについては次のページを参考にしました：

https://manabitimes.jp/math/2695

https://www.momoyama-usagi.com/entry/math-analysis24

https://www.momoyama-usagi.com/entry/math-analysis25
ヤコビ行列とヤコビアンの定義などについては次のページを参考にしました：

https://k-san.link/jacobian-def/

https://manabitimes.jp/math/1209

http://fnorio.com/0192Jacobian/Jacobian.html
球面の微小面積要素については次のページなどで示されています：

http://www.iwata-system-support.com/CAE_HomePage/vector/differential17/differential17.html

今回は単位球面の微小面積要素を考えたのでr=1の場合でr^2\sin(\phi)は\sin(\phi)になりました。
3点形式のレンダリング方程式の紹介がされているページとして次のものを参考にしました：

https://rayspace.xyz/CG/contents/LTE2/

 おわりにこの記事ではレンダラを作るうえで必要な数学的な知識として、ヤコビアンと半球上の立体角での積分について雑に説明しました。
立体角での積分とは単位球上で一様に積分をするという意味でした。
また、座標系を切り替えつつ積分値の物理の単位を正しく取り扱おうとするとよくヤコビアンが出てくるということを抑えておくとレンダラを作るうえで必要な数式が理解しやすいでしょう。
レンダラを作るうえで必要な数学的な知識は他にもたくさんありますが、まずはこの点を理解しておくと、モンテカルロレンダリングの論文を読むときに少し楽になると思います。
次回はモンテカルロ法についての説明を書こうと思っています。気が変わったら別のことを書くかもしれませんが……。

脚注
置換積分の公式の証明と例題 - 高校数学の美しい物語 https://manabitimes.jp/math/1159 ↩︎
ヤコビアンの定義・意味・例題（２重積分の極座標変換・変数変換）【微積分】 | k-san.link https://k-san.link/jacobian-def/ ↩︎ ↩︎
逆関数法とジオメトリサンプリング実装例 https://rayspace.xyz/CG/contents/geometry_sampling_implementation/ ↩︎
レンダリング方程式 (Rendering Equation) 2 https://rayspace.xyz/CG/contents/LTE2/ ↩︎