Zenn
Open7

ドメインモデルからGraphQLスキーマを自動生成できない？

GraphQL
#
DDD
#
er図
#
自動生成
masaorimasaori

ドメインモデルとは

要はER図。
なんだけど、DDDの文脈で言えば、決してDBの設計図ではない。もっと抽象度の高いレイヤーでビジネスに登場する概念とその関係を整理した図でありたい。

例えばこんな


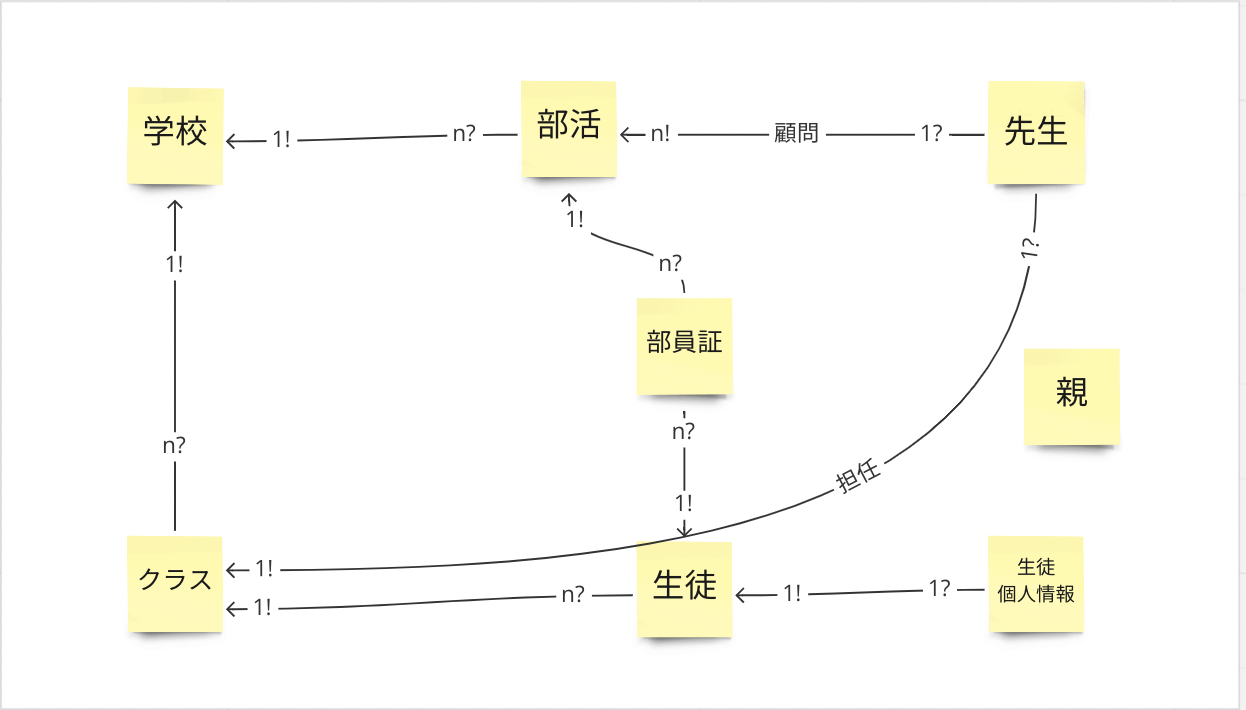
*図中の記号はあんまり一般的なものではないので注意してください。

masaorimasaori

GraphQLスキーマを自動生成するにあたってのゴール設定

仮説として、ドメインモデルにおいてのエンティティとそのリレーションが定まれば「絶対になきゃいけないクエリ」ってのを決めることができるはず、というのが前提にあります。それは自動生成でいいよね？という話。

よって、

クエリの種類は以下の二つとして分別します

  • リレーションから定まるもの
    • こっちが上でいう「絶対になきゃいけないクエリ」
  • 任意の検索クエリ
    • 文字列の部分一致とか

今回のスコープは前者のみ。後者の自動生成も不可能ではないと思われますが、ORMレベルのライブラリを構築するような話になってしまうので、現実的にはアプリケーションの仕様に応じて必要なものを用意することになると思います。

ミューテーション

基本的に各エンティティに対して

  • Create
  • Update
  • Delete

があれば十分

権限管理

今回は考えません。
リレーションから定められるものはあるはずなので、今後の課題。

認証系API

今回は考えません。
あと、 /me 的な、ブートストラップとなるAPIも対象外。

なので、基本的に考察対象は「リレーションから定まるクエリ」のみです。

masaorimasaori

何を考えればGraphQLクエリのスキーマが決められるか

あるエンティティ Hoge と Fuga があるとします。
それぞれ

type Hoge { ... }
type Fuga { ... }

としてなんらか型が定まっているとして、以下のようなスキーマが作れます (これらと、Hoge/Fugaの入れ替え)

Hoge {
   ...
    fuga: Fuga
}

Hoge {
   ...
    fuga: Fuga!
}

Hoge {
   ...
    fugas: [Fuga!]
}

Hoge {
   ...
    fugas: [Fuga!]!
}

これらと、ER図におけるHogeとFugaのリレーションどのように対応するかを考える

また、これとは別にクエリに与える引数を考える必要があります。
例えば以下のようなもの

getAll (引数なし)

type Query {
    hoges: [Hoge!]!
}

getById

type Query {
    hoge(id: Id): Hoge!
}

*!が付くつかないは後で考えます。

おそらくこれらのパターンがまだたくさんあるはずなので、ERから自動的に決定できるものが何かを模索します。

masaorimasaori

ちなみにですが、このスクラップは

こちらのチャンネルで相方のしかたと議論していることのまとめです。
まだまだ続く。

masaorimasaori

この辺りで議論したことです。
https://www.youtube.com/watch?v=xm_UJmv2LZs

必要なリレーションの種類を洗い出す - 準備

具体的に実用上必要そうなリレーションの種類を考えるには、RDBのルールを参照するのが手っ取り早そうです。
リレーションに関係しそうなのは、

  • Unique Constraint (ユニーク制約)
  • Foreign Key Constraint (外部キー制約)

ですね。

RDBにおける制約の意味

「制約」と言ってしまうと、あくまでもRDBの実装上のルールに聞こえてしまうので、ドメインモデル上で議論できるようなもう少し抽象的な概念として捉え直しておきましょう。

  • (外部キーに対する)Unique制約
    • 関係があったとしても高々一つだけ
  • 外部キー制約
    • 相手先が先に存在していないと、関係を持つことができない
  • (外部キーに対する)Non null制約
    • 必ず関係がなくてはならない

Unique制約は単純で、その有無が多重度 1とnに対応します。
外部キー制約とnull制約はちょっと詳しく考えておいた方が良さげです。

例えば、エンティティ Hoge と Fuga があり、

type Hoge { fugaId: FugaId, ... }
type Fuga { ... }

HogeのもつfugaIdに対して、以下の4パターンが考えられます

Non null制約あり Non null制約なし
外部キー制約あり *1 Hogeが存在するためには必ずFugaが存在しなければならない *2 HogeはFugaと独立して存在することができる
外部キー制約なし *3 無意味 *4 HogeはFugaと独立して存在することができる

*3 については「Hogeは必ずFugaと関係を持つ必要があるが、関係を持つFugaは存在していなくてもよい」と言う矛盾した状況になるので考えなくて良いです。
2と4が同じ意味になっていますが、関係がnullableな時点で「関係があってもなくても良い」ということになっており、Hogeに対してのFugaが先に存在してるかどうかがその意味に含まれてしまっています。(外部キー制約があっても、Fugaが存在していなかったら一旦nullを入れておいてFugaが生成されるのを待てばよいだけ)。FugaがいてもいなくてもHogeの存在に関係ないという意味で、独立して存在できるという言い回しにしました。

つまりありうる状況は、

  • Hogeが存在するためには必ずFugaが存在しなければならない
  • HogeはFugaと独立して存在することができる
    の二つしかないということがわかりました。

この2つの状況は互いに反対の状況を表していると言えますのでここに名前をつけるならば、FugaとHogeの間には 「存在の順序」についての依存関係 がある(もしくはない)と言えます。

この関係を今後「存在の依存」と呼んだりします。「HogeはFugaの存在に依存している」的ないい方です。

この関係を表す記号を用意します

今後このスクラップでは、以下の記号を使います

Unique制約あり Unique制約なし
存在の依存あり 1! n!
存在の依存なし 1? n?
!と?を併記する理由

単純に、

  • Typescriptなどのプログラミング言語ではnon-nullableには何もつけず、nullableを?で表す
  • GraphQLのスキーマではnon-nullableに!を使用し、nullableには何もつけない

というルールの変換がややこしくてたまに発狂するからです。
まああと、そもそもnullableとは意味が異なっていますのでそこらへんお気をつけください。

また、ER図として以下のように上の記号を記述します。

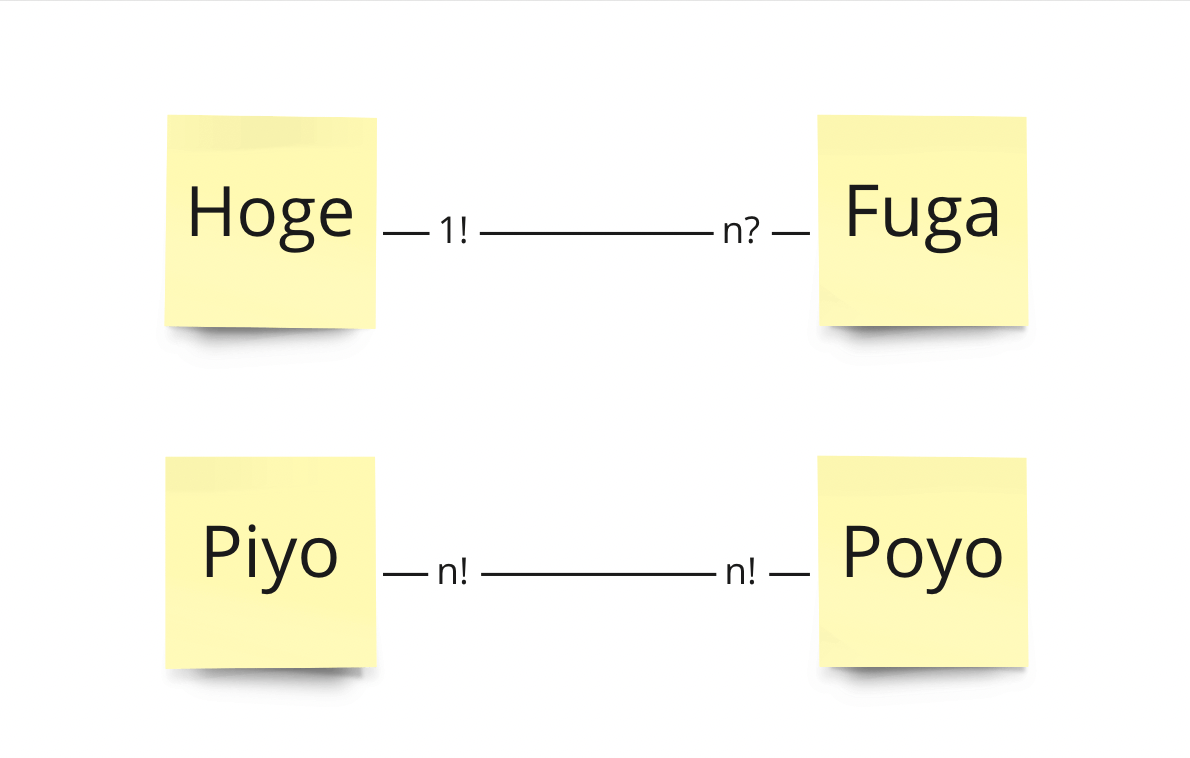
この具体例では、

Hoge - Fuga
  • Hogeは、Fugaから独立して存在することができて、かつ複数のFugaと関係を持つことができる
  • Fugaは、Hogeの存在に依存していて(FugaはHogeが先にいないと生成できない)、かつただ一つのHogeと関係を持つ
Piyo - Poyo
  • Piyoは、Poyoの存在に依存していて、かつ複数のPoyoと関係を持つことができる
  • Poyoは、Piyoの存在に依存していて、かつ複数のPiyoと関係を持つことができる

ありうるリレーション

以上から、ありうるリレーションは全部で10種類あることになります。

- 1! - 1! -
- 1! - n! -
- 1! - 1? -
- 1! - n? -
- n! - 1? -
- n! - n! -
- n! - n? -
- 1? - 1? -
- 1? - n? -
- n? - n? -
10種類内訳

エンティティ間に引かれている線の片側に置くことができるのは[1!, 1?, n!, n?]の4種類。
これを両端にそれぞれ配置することになるので、4 * 4 = 16 種類ですが、左右反転させたものは一緒に考えればいいのでそれを除くと10種類です。(そもそも左右対称のものは反転させても減らせないので、単純に/2にはならないです)

次の投稿で、これらのうちドメインモデルとして意味のありそうなものがどれかを絞り込んでいきます。多分。

masaorimasaori

結論から言うと、ドメインモデルで考えるべきリレーションは2種類になってしまいました。

残るのは、

- 1! - 1? -
- 1! - n? -

の二つのみです。

以下にその議論を列挙します。

1. 両端が!のリレーション

- 1! - 1! -
- 1! - n! -
- n! - n! -

これらは全て 理論上存在できません。
なぜなら、「Hogeが存在するためにはFugaが存在せねばならない」と「Fugaが存在するためにはHogeが存在せねばならない」は多重性に関わらず両立しないからです。当たり前ですね。

2. nと?について

まず、1!と1?の違いについて考えると、これは「必ず1つなければならない」と「0でもいい」という意味になります。
では、n!とn?の違いについて同じように当てはまると「必ず1つ以上なければならない」と「0でもいい」という意味になるのですが、現代の多くのプログラミング言語(GraphQL含む)は、 この違いを表現する能力を持ちません。つまりどちらも Hoge[] (HogeのArray) という表現になってしまうということです。

あえて Hoge[] | null (HogeのArrayのNullable) という書き方もできるかもしれませんが、nullでなかった時にそこに要素が入っているのかどうかを表現することはできないので、依然として曖昧です。

ですので我々のドメインモデル設計のルールとしては「n! と n?は見分けがつかない」というスタンスにします。かつ、全て0以上という意味になるということなので、これをn?と書きます。

すると以下のリレーションは、

- 1! - n? - => - 1! - n? -
- n! - n? - => - n? - n? -
- n! - 1? - => - n? - 1? -
- n? - n? - => - n? - n? -

となり、重複が一個省けます。

3. 両端が?のリレーション

- 1? - 1? -
- 1? - n? -
- n? - n? -

これらは理論上存在可能ですが「双方が双方に独立して存在している」という状況なのでそのリレーションを「両方の存在に依存してその関係を媒介するエンティティ」として表現した方が自然では？という結論になりました。ですのでこれらは、

A - 1? - 1? - B => A - 1! - 1? - C - 1? - 1! - B
A - 1? - n? - B => A - 1! - 1? - C - n? - 1! - B
A - n? - n? - B => A - 1! - n? - C - n? - 1! - B

のように分解されます。このドメインモデルは、このような分解規則を持つ、という言い方もできます。

以上、まとめると以下の3つの簡約規則が作られます。

  1. 両端が!のリレーションは削除(存在できない)
  2. n!はn?に書き換え(見分けがつかない)
  3. 両端が?のリレーションを上記のルールで分解

これらの規則を前回記事の10このリレーションに適用すると、以下の二つだけが残ります。

- 1! - 1? -
- 1! - n? -

記法

今後この記事とYoutube配信中では、こちらの表記方法も使用しますが、この二つをよく見ると

  • どちらかの端が!で他方は? という非対称性がある
  • 片側は必ず1でもう片方が1 or n

ということがわかりますので、前者の非対称性を「矢印」で表し、後者のためには?側の数字を添えるだけで表現ができます。
矢の向き先を!側にすることで「存在の依存」の関係もわかりやすくなるでしょう。

ですので、以下のような記法も取り入れてわかり良い方を使っていきます。

masaorimasaori

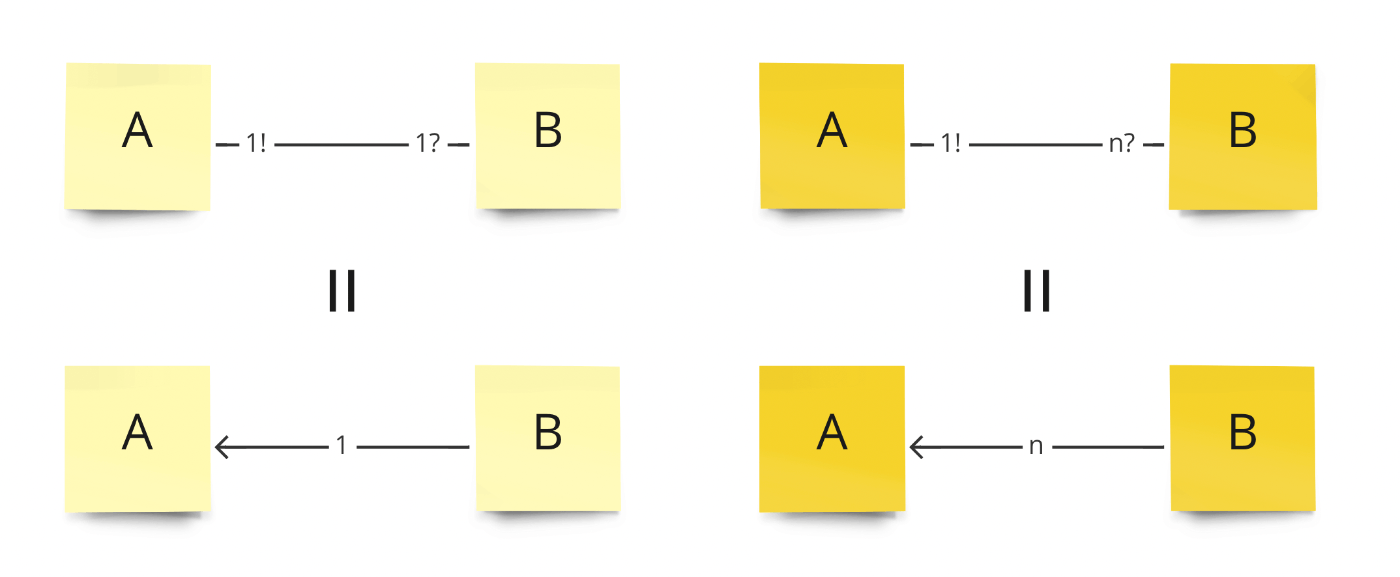
前回の議論から、ドメインモデルに登場するリレーションは「1 or nの矢印」2種類ということがわかりました。つまりグラフとして捉えるなら「有向グラフ」に近いものとして考えられそうです。
実は、前回の変換規則3を導入することで、左右対称のリレーションが全て分解されていなくなっているので、全てを「有向的」なリレーションのみで表現できるという単純化ができるというメリットもありました。

ここから具体的に、ここまでに設定されたドメインモデルの登場要素とGraphQLのスキーマを対応関係を考えていくわけですが、その前に今回設定したドメインモデルの「要素」たちがどのような構造を持つのかをみておきたいです。ここにキレイな構造があれば、今回導入したルールセットの妥当性につながりますし、のちの解析もしやすくなったりしないかな？という目論みです。

とはいえ、ひろのもしかたも数学的な構造についてはど素人なので、これ！という正解については曖昧にして、思いつくものを列挙するにとどめて先に進みます。

この辺りで議論しました
YouTubeのvideoIDが不正ですhttps://youtube.com/live/D5f32xpY_E8

ドメインモデルの構造

順序関係・グラフ

まず、矢印の種類が2種類になっていることから 順序関係 や グラフ ではありません。
僕の調査範囲では、エッジに複数の種類を与えるようなグラフは見つけられませんでした。エッジの集合とソースとターゲットを与える写像がそれぞれ2種類になるというだけなので、このような拡張は可能だと思われますが、これにいい感じの名前がもしついていたらどなたか教えてください🙇

圏

複数の矢印持つことができてそれらが見分けられる性質を持つということで、 圏 として捉える方向性はありそうです。
この場合、合成演算と恒等射の定義が必要になります。

恒等射

恒等射については、エンティティの何らかの意味での自己参照に対応してそうです。
ですが、今回矢印の意味を存在の依存、つまり「矢印の根元は矢印の先が先に存在しないと存在し得ない」というようにしているので、自己参照に関してはそもそも矛盾が発生してそうですね。

存在の依存というのは要は外部キー制約なので、「自分のプライマリキーに対しての外部キー制約」の場合に絞るならば「自分のIDがないと自分は存在できない」という「そりゃそうだよね」という理屈になるので、これのみを特別扱いして恒等射としてしまうのはアリかもしれません。

ただし、その他の自己参照(Userが持つparentUserId的な)については圏構造とは関係なく見直しが必要そうです。

合成則

合成演算を定めるには

  • 合成した時に矢印の意味が変わらないこと
  • 合成した時に多重性がどう変化するかのルール

を確認する必要があります。

前者は、存在の依存は推移的と捉えて問題なさそうなのでOK

後者は

1 ○ 1 := 1
1 ○ n := n
n ○ 1 := n
n ○ n := n

で問題なさそうです。

生成集合？

ただし、圏として捉える場合、合成演算により「芋づる式に」リレーションが増えていくことになります。
つまり、最初に設定した「直接のリレーション」を飛び越えて「ショートカットされたリレーショん」が全てのエンティティ間に発生しうるということです。
これをどう捉えるべきかはのちの課題です。

例えば下図の赤色のリレーションが合成演算によって生成されたリレーションです

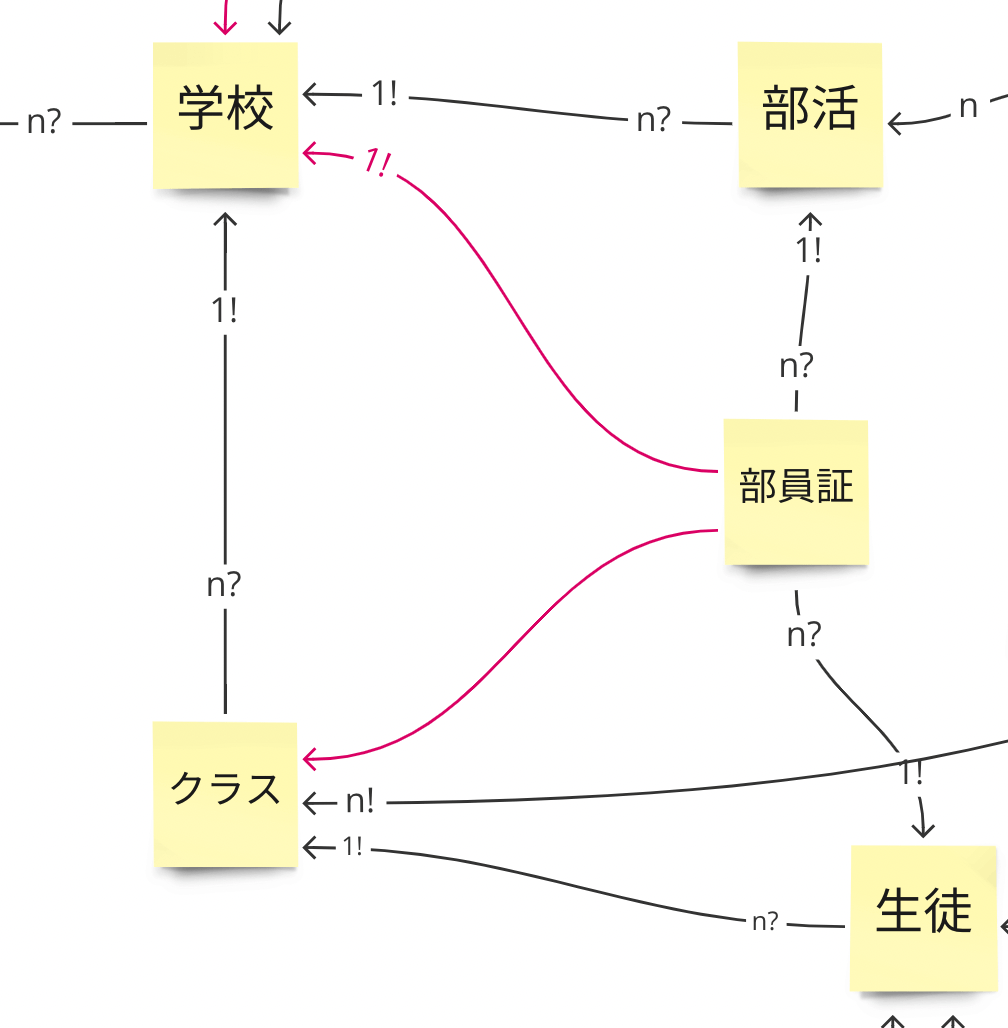
射の種類？

もう一つ課題として「射が２種類ある」という状況を圏論的にどう表すのかはよくわかっていません。
何らかの圏やグラフ構造そのものを射とみなす、みたいなことをするのでしょうか？