再帰による繰り返し処理(Haskell)

この記事では再帰関数に関する基本的なトピックをご紹介します。
命令型言語では繰り返し処理を行うのにfor/whileを使っていました。しかし関数型言語ではfor/whileの仕組みはありません。カウントした数値を更新する際に値を変更してしまうからです。 Haskellでは変数の値を変更するなどの副作用を禁止しています。

そこで使われるのが再帰の仕組みです。再帰とは関数の中で自分自身の関数を呼び出す仕組みです。 処理を行う関数を何度も呼び出せばそれだけで繰り返し処理ができますよね。再帰と聞くと難しそうですが日常生活でもたくさんあります。

・レジの会計（商品を取ってスキャン、買い物カゴが空になるまで繰り返す）
・トイレ掃除（汚れを見つけたら拭く、全部が綺麗になるまで繰り返す）
・洗濯物を畳む（1枚ずつ洋服を畳んでいく、家族全員分を畳むまで繰り返す）

目的を達成するまで同じことを繰り返すというのは再帰と同じ考え方が使われています。（どの技術書でもいってますが）再帰をマスターするには何度もコードを書くのが１番です。3つの関数を例に再帰に関する基本的なトピックを学んでいきます。

head'関数：パターンマッチ、x:xsパターン
sum'関数：再帰を使った関数
take'関数：複数の引数

head関数(パターンマッチ/x:xs/error関数)

(再帰ではないですが)まずはカンタンなhead関数で感覚を掴みます。head関数は先頭の要素を取り出す関数です。head'として実装した関数がこちらです。

head' :: [a] -> a
head' [] = error "list is empty" --(1)引数がなかった場合
head' (x:xs) = x  --(2)引数があった場合

list = [1,2,3,4,5]
main = print $ head' list
-- 実行結果「1」

すごくシンプルですが、再帰を理解するため重要なトピックが3つあります。

(1)パターンマッチ

再帰を実現する上で大切なのがパターンマッチです。パターンマッチとは引数の値による条件分岐の仕組みです。(1)引数がなかった場合,(2)引数があった場合でキレイに場合分けができています。

要するに再帰とは(1)終了条件,(2)それ以外のパターンの集まりです。 1番最初にまずは終了する場合の処理を定義します。その後に残りのパターンを1つ1つ定義していきます。これによって箇条書きでそれぞれのパターンを定義できます。

(2)x:xsパターン

リストを先頭/それ以外へと分解できる仕組みです。x、xsは命名規約ではありませんが、この名前を使うのが一般的です。（xは単一、xsは複数(s)という意味が込められているようです。）空リストではない場合にx:xsパターンが発動する仕組みとなっています。

ここではリストを[1]と[2,3,4,5]へと分解しています。そして先頭の要素xつまり[1]を出力にかけています。x:xsパターンは再帰で何度も使うことになるので覚えておいて下さい。

(3)error関数

errorは関数です。文字列を引数に取り、その文字列を使ってランタイムエラーを起こします。終了条件や何も要素がなかった場合にerror関数をよく使いますので覚えておいて下さい。（error関数を使わずに、空リスト[]や数値の0を返却する場合もあります。）

sum関数(再帰を使った関数)

再帰とは関数の中で関数それ自身を呼び出すための仕組みでした。ここから再帰を使った関数の仕組みをご紹介します。リストの要素の数値を全て足し算する関数として、sum`関数を考えてみます。

sum' :: Num a => [a] -> a
sum' [] = 0
sum' (x:xs) = x + (sum' xs)

main = print $ sum' [1,2,3]
--実行結果「6」

2行目(空リストだった場合)

2行目で空リスト[]だった場合の処理を決めています。今回は数値同士の足し算なので0を返却します。

3行目(空リストでない場合)

リストが空でなかった場合、3行目の処理が発動します。関数の中で更に関数自身を呼び出している点に注目して下さい。=を挟んで左側：sum' (x:xs)、右側：x + (sum' xs)に分けてご説明します。

■左側：add' (x:xs)
sum' (x:xs)では(空でない)リストを受け取って、それをx:xs(先頭/それ以外)へと分解します。=の右側では分解した後の処理を定義しています。

■右側：x + (sum' xs)
x + (sum' xs)を処理として定義しています。xと(sum' xs)を足し算しようとしたところで、更にsum'関数が呼び出されます。そこで残りの要素xsに対してsum'関数が適用されます。

これをリストがなくなるまで繰り返します。最後までsum`を適用して全てが数値になったところで、逆に上へと遡って足し算を行います。図にすると以下のような形です。

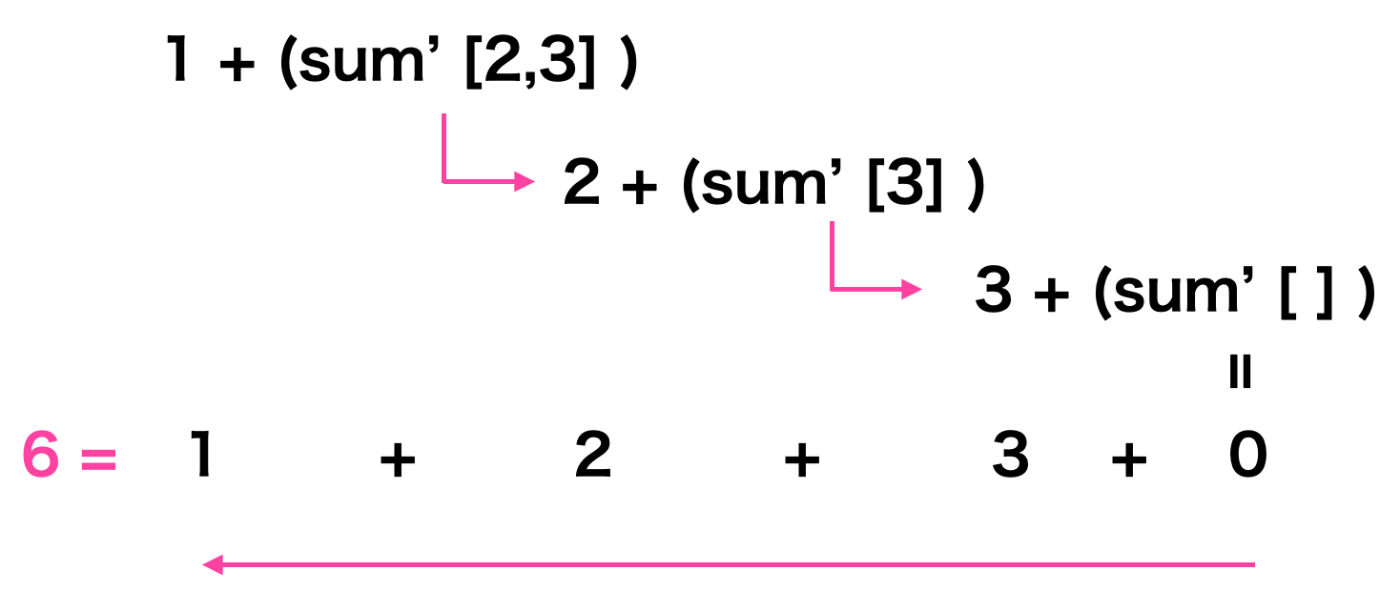
数値として計算できるようになるまでsum'関数が適用されていく点に注目して下さい。計算をしようとしたところで更にsum`が展開されていきます。

take関数(複数の引数)

リストの先頭から指定された要素数を出力するtake関数を実装します。(1)取り出す要素の個数、(2)リスト で計2つの引数を指定する必要がある点に注意して下さい。take'として実装したのが以下です。

take' :: Int -> [a] -> [a]
take' 0 _ = []
take' n [] = []
take' n (x:xs) = x : take'(n-1) xs

main = print $ take'[1,2,3]
-- 実行結果「[1,2]」

1行目では型を定義しています。Int型の整数とリストを受け取って、リストを返却する関数となっています。

2/3行目(処理が終了する場合)

2/3行目では処理が終了するパターンを定義しています。

2行目：取り出す要素数が0だった場合
３行目：リストが空になった場合

上記はどれも処理が終了するパターンなので、空リスト[]を返却するようにしました。

4行目(要素数/リスト共に1以上の場合)

４行目では要素数/リスト共に1以上の場合を定義しています。引数の1つ目(Int型の整数の方)をnとして受け取り、リストを(x:xs)へ分解して受け取っています。

=の右側では受け取った後の処理を定義しています。ここではcons演算子:で更に新しくリストを作っています。先頭のリストxとtake'(n-1) xsをリストとして結合しようとしています。結合しようとしたところでtake'(n-1) xsはそのままでは計算できないので、更にtake'がxsへと適用されます。それがリストが空になるまで繰り返されます。図にすると以下です。

take'(n-1) xsはそのままでは計算できません。最後まで関数の適用を繰り返して全てが数値になったところで、リストへと結合されます。(n-1)とすることで、最後の要素以外を除いている点に注目して下さい。

リストを操作する関数の多くは再帰で作れることができます。試しに自分でも色々と作ってみると理解が深まるのではないかと思います。