Rによる計数データ(カテゴリカルデータ)解析
はじめに
本記事では、医療分野における計数データの基本的な解析のRでの実装を紹介する。計数データは人数やイベント回数のような整数値をとるデータで、カウントデータやカテゴリカルデータと呼ばれることもある。本記事では、2項分布の解析、2標本におけるオッズ比、リスク比、リスク差の推定、また多群での解析など幅広く扱う。
生物統計の初学者よりは一定の知識がある者を対象とし数式やRの使用方法に関する記述を省いたためわかりづらい箇所があるかもしれないが、ご容赦いただければ幸いである。
【参考文献】
目次
- Package
- 仮想的なランダム化比較試験のデータ生成
- データの要約
- カテゴリ化した変数の要約
- 二項分布の解析
- Wald法
- Score法
- Exact法
- 2*2表の解析
- 独立性の検定
- 粗解析によるリスク比、オッズ比、リスク差
- 層別解析による共通リスク比、オッズ比、リスク差(Mantel-Haenzel推定量)
- 回帰分析によるリスク比、オッズ比、リスク差
- 対応のある検定(McNemar test)
- (補足)McNemar testのI*J表への拡張
- I*J表の解析
- 2*J 表
- I*2 表
- I*J 表(名義尺度*名義尺度)
- I*J 表(順序尺度*順序尺度)
- サンプルサイズ計算
- 単群のサンプルサイズ計算
- 対応のない2標本のサンプルサイズ計算
- McNemar検定のサンプルサイズ計算
- まとめ
- (メモ)今後、追加する可能性のある解析
Package
利用するPackageは以下の通りである。
#package
library(tidyverse)
library(gtsummary)
library(epiR)
library(geepack)
library(broom)
library(coin)
library(TrialSize)
仮想的なランダム化比較試験のデータ生成
本記事では、仮想的なランダム化比較試験(RCT)のデータを生成し解析した。仮想的なRCTとして、200名の2型糖尿病患者もしくは予備群を対象にある薬剤の効果を検討する試験を考える。割付群としては、Placebo群、2.0 mg, 5.0mg, 10.0mg群の4群に均等に割り付け、アウトカムはHbA1cの変化量とした。データ生成時には、アウトカムは連続量として与えているが、本記事内では計数データの解析を扱うためカテゴリ化した変数のみを解析対象とする。
#データ生成
set.seed(1234)
n <- 200
th1 <-
data.frame(ID = c(1:n),
pre_drug = sample(c(0,1), n, replace=TRUE, prob = c(.6, .4)) ) %>%
mutate(TRT = case_when(
ID <= n/4 ~ "placebo",
ID <= 2*n/4 ~ "2.0 mg",
ID <= 3*n/4 ~ "5.0 mg",
ID <= n ~ "10.0 mg")) %>%
mutate(TRT_c = case_when(
ID <= n/4 ~ "0",
ID <= 2*n/4 ~ "1",
ID <= 3*n/4 ~ "2",
ID <= n ~ "3")) %>%
mutate(TRT_c2 = ifelse(ID <= n/4,"0","1")) %>%
mutate(dose = case_when(
ID <= n/4 ~ 0,
ID <= 2*n/4 ~ 2,
ID <= 3*n/4 ~ 5,
ID <= n ~ 10)) %>%
mutate(pre = round(runif(n=n, min=6.5, max=7.4),2)) %>%
mutate(pre = ifelse(pre_drug == 1, pre-0.2, pre)) %>%
mutate(post = case_when(
ID <= n/4 ~ round(pre + rnorm(n=n/4, mean=0.2, sd=0.4),2),
ID <= 2*n/4 ~ round(pre + rnorm(n=n/4, mean=0, sd=0.4),2),
ID <= 3*n/4 ~ round(pre + rnorm(n=n/4, mean=-0.2, sd=0.4),2),
ID <= n ~ round(pre + rnorm(n=n/4, mean=-0.4, sd=0.4),2))) %>%
mutate(post = ifelse(pre_drug == 1, post-0.1, post)) %>%
mutate(change = post - pre)
print(head(th1))
| 変数名 | 概要 |
|---|---|
| ID | ID |
| pre_drug | 試験前の薬の服用有無 |
| TRT | 割付群 |
| TRT_c | Placebo群、2.0 mg, 5.0mg, 10.0mgをそれぞれ(0, 1, 2, 3)で表記 |
| TRT_c2 | Placebo群(0)と治療群(1)の2値 |
| pre | ベースラインでのHbA1c [%] |
| post | 試験終了時のHbA1c [%] |
| change | post - pre |
## ID pre_drug TRT TRT_c TRT_c2 dose pre post change
## 1 1 0 placebo 0 0 0 7.09 7.48 0.39
## 2 2 1 placebo 0 0 0 6.78 7.16 0.38
## 3 3 1 placebo 0 0 0 6.59 6.76 0.17
## 4 4 1 placebo 0 0 0 6.99 7.37 0.38
## 5 5 1 placebo 0 0 0 6.77 6.99 0.22
## 6 6 1 placebo 0 0 0 6.96 7.36 0.40
th1のpre, post, changeをもとにカテゴリ化した変数をいくつか作成した。
th2 <- th1 %>%
mutate(pre2 = ifelse(pre < 7.0,1,0)) %>%
mutate(post2 = ifelse(post < 7.0,1,0)) %>%
mutate(change2 = ifelse(change < 0,1,0)) %>%
mutate(change3 = case_when(
change < -0.5 ~ 2,
change < 0 ~ 1,
change < 0.5 ~ -1,
TRUE ~ -2 ))
print(head(th2))
| 変数名 | 概要 |
|---|---|
| pre2 | preのHbA1cが7.0%未満なら1、7.0%以上なら0の指示変数 |
| post2 | postのHbA1cが7.0%未満なら1、7.0%以上なら0の指示変数 |
| change2 | HbA1cが改善していれば1,していなければ0の指示変数 |
| change3 | HbA1cが0.5%以上減少していれば2,改善で1, 増加で-1, 0.5%以上の増加で-2 をとる変数 |
## ID pre_drug TRT TRT_c TRT_c2 dose pre post change pre2 post2 change2
## 1 1 0 placebo 0 0 0 7.09 7.48 0.39 0 0 0
## 2 2 1 placebo 0 0 0 6.78 7.16 0.38 1 0 0
## 3 3 1 placebo 0 0 0 6.59 6.76 0.17 1 1 0
## 4 4 1 placebo 0 0 0 6.99 7.37 0.38 1 0 0
## 5 5 1 placebo 0 0 0 6.77 6.99 0.22 1 1 0
## 6 6 1 placebo 0 0 0 6.96 7.36 0.40 1 0 0
## change3
## 1 -1
## 2 -1
## 3 -1
## 4 -1
## 5 -1
## 6 -1
データの要約
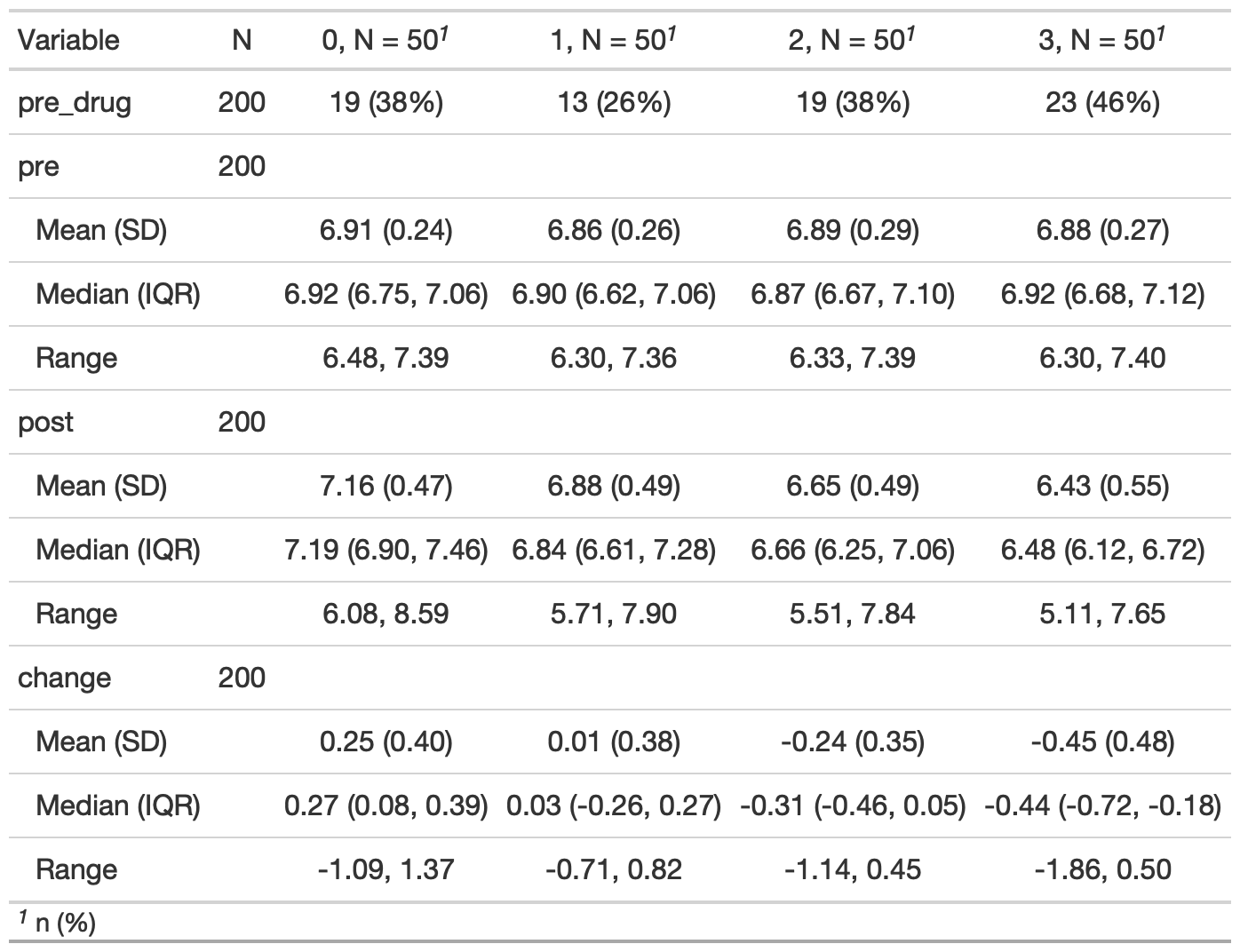
各群ごとに、カテゴリカル変数については人数を集計し割合を算出し、連続量に対しては平均(標準偏差)、中央値(IQR)、範囲を算出した。
#データの要約
table1 <- th1 %>%
dplyr::select(pre_drug,pre,post,change,TRT_c) %>%
tbl_summary(
by = TRT_c,
type = all_continuous() ~ "continuous2",
statistic = all_continuous() ~ c("{mean} ({sd})","{median} ({p25}, {p75})", "{min}, {max}"),
missing = "no") %>%
add_n() %>%
modify_header(label = "**Variable**")
カテゴリ化した変数の要約
th2で新たに定義したカテゴリ化した変数について、いくつかの分類のもと表を作成した。
TRT_c(Placebo群、2.0 mg, 5.0mg, 10.0mg群)とchange3(4 levels)の4*4のクロス表を作成した。
table2 <- th2 %>%
tbl_cross(row = TRT_c, col = change3, percent = "row")

TRT_c(Placebo群、2.0 mg, 5.0mg, 10.0mg群)とchange2(2 levels)の4*2のクロス表を作成した。
table3 <- th2 %>%
tbl_cross(row = TRT_c, col = change2, percent = "row")

TRT_c2(Placebo群、投薬群)とchange2(2 levels)の2*2のクロス表を作成した。
table4 <- th2 %>%
tbl_cross(row = TRT_c2, col = change2, percent = "row")

適宜、紹介する手法に合わせたクロス表を利用する。
二項分布の解析
二項分布の解析を行った。単群の計数データに対する解析になる。そのため、投薬群のみを用いて解析した。
#2項分布の解析
th3 <- th2 %>%
filter(TRT_c2 == "1") %>%
summarise(
n = n(),
x = sum(change2))
一般に、2項分布における
Wald法
関数による算出がわからなかったため、式から算出した。
##Wald
x <- th3$x
n <- th3$n
pi <- x/n
v <- x*(n-x)/(n^3)
p0 <- 0.5
z <- (pi-p0)/sqrt(v)
p_val <- 2*(1-pnorm(abs(z)))
wald_cl <- round(c(max(0,pi-1.96*sqrt(v)),min(pi+1.96*sqrt(v),1)),2)
print(p_val)
## [1] 1.490234e-05
点推定値と95%信頼区間についてWald法では0.67[0.59-0.74]となった。
print(c(round(pi,2),wald_cl))
## [1] 0.67 0.59 0.74
Score法
点推定値と95%信頼区間についてScore法では連続補正なしの場合には、0.67[0.59-0.74]となった。連続補正ありの場合でも0.67[0.59-0.74]となった。
##Score
prop.test(x,n, p=p0, correct=F) #連続補正なし
##
## 1-sample proportions test without continuity correction
##
## data: x out of n, null probability p0
## X-squared = 16.667, df = 1, p-value = 4.456e-05
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
## 0.5878976 0.7371124
## sample estimates:
## p
## 0.6666667
prop.test(x,n, p=p0, correct=T) #連続補正あり
##
## 1-sample proportions test with continuity correction
##
## data: x out of n, null probability p0
## X-squared = 16.007, df = 1, p-value = 6.312e-05
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
## 0.5844682 0.7401791
## sample estimates:
## p
## 0.6666667
Exact法
点推定値と95%信頼区間についてExact法では、0.67[0.59-0.74]となった。
##Exact
binom.test(x,n, p=p0, alternative="two.sided")
##
## Exact binomial test
##
## data: x and n
## number of successes = 100, number of trials = 150, p-value = 5.448e-05
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.5851570 0.7414436
## sample estimates:
## probability of success
## 0.6666667
2*2表の解析
2*2表の解析を紹介するために、TRT_c2とchange2によるクロス表を解析した。
x <- xtabs(formula = ~TRT_c2+change2, data = th2)
x
## change2
## TRT_c2 0 1
## 0 41 9
## 1 50 100
独立性の検定
Yatesの連続補正を加えた
## chisq
chisq.test(x)
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: x
## X-squared = 33.881, df = 1, p-value = 5.858e-09
Exact検定のp値は以下のように算出できる。
## exact
fisher.test(x)
##
## Fisher's Exact Test for Count Data
##
## data: x
## p-value = 2.451e-09
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
## 3.925819 22.794715
## sample estimates:
## odds ratio
## 9.00197
粗解析によるリスク比、オッズ比、リスク差
リスク比、オッズ比、リスク差の推定について紹介する。epi.2by2を用いれば簡単に推定できる。リスク比は"Inc risk ratio"、オッズ比は"Odds ratio"、リスク差[%]は"Attrib risk in the exposed *"を見れば良い。
##RR, OR, RD(Attrib risk in the exposed|ARisk)
x2 <- matrix(rev(as.vector(x)), ncol=2, byrow = F)
print(x2)
## [,1] [,2]
## [1,] 100 50
## [2,] 9 41
epi.2by2(x2, method = "cohort.count", conf.level = .95)
## Outcome + Outcome - Total Inc risk * Odds
## Exposed + 100 50 150 66.7 2.00
## Exposed - 9 41 50 18.0 0.22
## Total 109 91 200 54.5 1.20
##
## Point estimates and 95% CIs:
## -------------------------------------------------------------------
## Inc risk ratio 3.70 (2.03, 6.76)
## Odds ratio 9.11 (4.10, 20.22)
## Attrib risk in the exposed * 48.67 (35.62, 61.72)
## Attrib fraction in the exposed (%) 73.00 (50.69, 85.22)
## Attrib risk in the population * 36.50 (23.81, 49.19)
## Attrib fraction in the population (%) 66.97 (42.46, 81.04)
## -------------------------------------------------------------------
## Uncorrected chi2 test that OR = 1: chi2(1) = 35.817 Pr>chi2 = <0.001
## Fisher exact test that OR = 1: Pr>chi2 = <0.001
## Wald confidence limits
## CI: confidence interval
## * Outcomes per 100 population units
層別解析による共通リスク比、オッズ比、リスク差(Mantel-Haenzel推定量)
計数データの交絡因子の対処としては、大きく層別解析と回帰分析がある。回帰分析も後述するが、ここでは層別解析を取り上げる。層別解析のアイデアは、交絡因子により複数の層に分類し、各層ごとに推定を行いその結果を統合することで共通効果を推定するというものである。交絡因子がカテゴリカル変数であればよいが、連続量の場合にはカテゴリカル変数に変換するか回帰分析により調整することになる。
各層ごとの結果の統合方法としては、重み付き最小二乗推定量と、Mantel-Haenzel推定量がしばしば用いられるが、ここではMantel-Haenzel推定量(MH推定量)を紹介する。
試験前の投薬有無のpre_drugを調整する層別解析を行った。先ほど同様に、リスク比は"Inc risk ratio"、オッズ比は"Odds ratio"、リスク差[%]は"Attrib risk in the exposed *"を見れば良いが、共通効果を見る場合は(M-H)を確認する。粗解析(crude)は層別しない場合の解析であるため、先ほどの結果と一致する。今回はRCTを想定しており、データ上で交絡が生じていないため粗解析と層別解析の結果はほぼ一致する。
##staratified RR, OR, RD
th3 <- th2 %>%
dplyr::select(TRT_c2, change2, pre_drug) %>%
mutate(TRT_c3 = ifelse(TRT_c2==1,-1,0)) %>%
mutate(change3 = ifelse(change2==1,-1,0))
stratified_x <- table(th3$TRT_c3, th3$change3, th3$pre_drug,
dnn = c("TRT", "Outcome", "Pre_Drug"))
print(stratified_x)
## , , Pre_Drug = 0
##
## Outcome
## TRT -1 0
## -1 60 35
## 0 5 26
##
## , , Pre_Drug = 1
##
## Outcome
## TRT -1 0
## -1 40 15
## 0 4 15
epi.2by2(stratified_x, method = "cohort.count", conf.level = 0.95)
## Outcome + Outcome - Total Inc risk * Odds
## Exposed + 100 50 150 66.7 2.00
## Exposed - 9 41 50 18.0 0.22
## Total 109 91 200 54.5 1.20
##
##
## Point estimates and 95% CIs:
## -------------------------------------------------------------------
## Inc risk ratio (crude) 3.70 (2.03, 6.76)
## Inc risk ratio (M-H) 3.71 (2.03, 6.78)
## Inc risk ratio (crude:M-H) 1.00
## Odds ratio (crude) 9.11 (4.10, 20.22)
## Odds ratio (M-H) 9.31 (4.17, 20.81)
## Odds ratio (crude:M-H) 0.98
## Attrib risk in the exposed (crude) * 48.67 (35.62, 61.72)
## Attrib risk in the exposed (M-H) * 48.78 (35.05, 62.50)
## Attrib risk (crude:M-H) 1.00
## -------------------------------------------------------------------
## M-H test of homogeneity of PRs: chi2(1) = 0.042 Pr>chi2 = 0.838
## M-H test of homogeneity of ORs: chi2(1) = 0.013 Pr>chi2 = 0.909
## Test that M-H adjusted OR = 1: chi2(1) = 35.834 Pr>chi2 = <0.001
## Wald confidence limits
## M-H: Mantel-Haenszel; CI: confidence interval
## * Outcomes per 100 population units
回帰分析によるリスク比、オッズ比、リスク差
リスク比、オッズ比、リスク差は回帰分析からも推定することができ、共変量の調整を行える。層別解析とは異なり連続量の調整も行えるが、その分モデルの仮定は追加されることになる。基本的には一般化線形モデル(GLM)[1]の枠組みで解析できる。オッズ比はLink関数にLogit、リスク比はLink関数にLog、リスク差はLink関数に恒等関数を用いればよい。
ただし、対数二項分布だとうまく計算できなかったので、今回はリスク比の推定には修正ポアソン回帰を用いた。修正ポアソン回帰はポアソン回帰の過分散に対処するために分散にロバスト分散を利用する手法であり、ロバスト分散を使うためにGEEのpackageを利用している。
層別解析同様に、pre_drugで調整して推定した。
##REG
OR_model <- glm(change2 ~ TRT_c2 + pre_drug, data=th2, binomial(link="logit"))
# RR <- glm(change2 ~ TRT_c2 + pre_drug, data=th2, binomial(link = "log"))
RR2_model <- geeglm(change2 ~ TRT_c2 + pre_drug, data=th2, poisson(link = "log"), id=ID)
RD_model <- glm(change2 ~ TRT_c2 + pre_drug, data=th2, binomial(link = "identity"))
log_OR <- OR_model[["coefficients"]][["TRT_c21"]]
log_OR_cl <- confint(OR_model)[2, ]
OR <- c(exp(log_OR),exp(log_OR_cl))
RR <- tidy(RR2_model, conf.int = TRUE, conf.level = 0.95, exponentiate = TRUE)[2,c(2,6,7)] %>% as.matrix
RD <- c(RD_model[["coefficients"]][["TRT_c21"]],confint(RD_model)[2, ])
names(OR) <- c("Estimate","95%cl_low","95%cl_high")
names(RD) <- c("Estimate","95%cl_low","95%cl_high")
print(OR)
オッズ比
調整オッズ比の点推定値と95%信頼区間は9.35[4.36-22.1]となった。
## Estimate 95%cl_low 95%cl_high
## 9.350588 4.360122 22.069783
print(RR)
リスク比(修正ポアソン回帰)
調整リスク比の点推定値と95%信頼区間は3.71[2.03-6.77]となった。
## estimate conf.low conf.high
## [1,] 3.711331 2.034354 6.770687
print(RD)
リスク差
調整リスク差の点推定値と95%信頼区間は0.49[0.35-0.60]となった。
## Estimate 95%cl_low 95%cl_high
## 0.4858404 0.3453432 0.6036405
対応のある検定(McNemar test)
対応のあるデータを比べる場合には、McNemar testが用いられる。投薬群に限定し、HbA1cが7.0%の閾値で2値化した変数を試験前後で比較する。McNemar testは、
##McNemar test
th4 <- filter(th2, TRT_c2 ==1 )
mcnemar <- xtabs(formula = ~pre2 + post2, data = th4)
print(mcnemar)
## post2
## pre2 0 1
## 0 27 28
## 1 14 81
mcnemar.test(mcnemar, correct = FALSE)
##
## McNemar's Chi-squared test
##
## data: mcnemar
## McNemar's chi-squared = 4.6667, df = 1, p-value = 0.03075
(補足)McNemar testのI*J表への拡張
McNemar testは2*2表で利用されるが、さらにI*J表拡張した手法としてMcNemar-Bowker Testが存在する。プログラムはMcNemar testと同様だが、対称性の検定を行っていることに注意する。
##(補足)McNemar-Bowker Test
tmp <- matrix(c(19,12,12,9,34,12,0,12,38), ncol=3, byrow=TRUE)
print(tmp)
## [,1] [,2] [,3]
## [1,] 19 12 12
## [2,] 9 34 12
## [3,] 0 12 38
mcnemar.test(tmp, correct = FALSE)
##
## McNemar's Chi-squared test
##
## data: tmp
## McNemar's chi-squared = 12.429, df = 3, p-value = 0.00605
I*J表の解析
対応のないI*J表のデータ解析を紹介する。本記事内では、行が治療等の割付群、列がアウトカムを表しており、I*2表、2*J表、I*J表に分けてコードを示す。しかし基本的な考え方は同じであるため、はじめに基本的な考え方を提示する。
2*2表からI*J表の解析を考えるにあたり、最も考慮すべきは尺度が名義尺度か順序尺度かの区別をする必要がある点である。
名義尺度*名義尺度であればピアソンの
順序尺度の場合は順序を考慮するためのスコアを割り当てることを考える。例えば、順序のある
クロス表の
"xxx"と呼ばれるなどという記載がある場合には、数理的に親しい概念が存在することが多い。例えば、I*J表で行と列ともに順序尺度の場合の解析はMantelの相関検定と呼ばれる。確かにMantelの相関検定の検定統計量
以下、Rのコードを紹介する。chisq_testでsocresを指定すればスコアを割り当てて解析することができる。
2*J 表
2*J 表で列が順序尺度のとき、特にCochran-Armitage検定と呼ばれる。
## 2*J 表
x_2_j <- xtabs(formula = ~TRT_c2 + change3, data = th2)
x_2_j
## change3
## TRT_c2 -2 -1 1 2
## 0 8 33 7 2
## 1 6 44 67 33
cmh_test(x_2_j)
##
## Asymptotic Generalized Cochran-Mantel-Haenszel Test
##
## data: change3 by TRT_c2 (0, 1)
## chi-squared = 37.097, df = 3, p-value = 4.388e-08
chisq_test(x_2_j, scores = list("change3"= c(1,2,3,4)))
##
## Asymptotic Linear-by-Linear Association Test
##
## data: change3 (ordered) by TRT_c2 (0, 1)
## Z = -5.6872, p-value = 1.292e-08
## alternative hypothesis: two.sided
I*2 表
I*2 表で行が順序尺度でスコアに単に1, 2, 3,...と割り当てたとき、Wilcoxon検定と呼んだりする。
## I*2 表
x_i_2 <- xtabs(formula = ~TRT_c + change2, data = th2)
x_i_2
## change2
## TRT_c 0 1
## 0 41 9
## 1 28 22
## 2 14 36
## 3 8 42
cmh_test(x_i_2)
##
## Asymptotic Generalized Cochran-Mantel-Haenszel Test
##
## data: change2 by TRT_c (0, 1, 2, 3)
## chi-squared = 52.544, df = 3, p-value = 2.294e-11
chisq_test(x_i_2, scores = list("TRT_c"= c(1,2,3,4)))
##
## Asymptotic Linear-by-Linear Association Test
##
## data: change2 by TRT_c (0 < 1 < 2 < 3)
## Z = -7.1759, p-value = 7.185e-13
## alternative hypothesis: two.sided
chisq_test(x_i_2, scores = list("TRT_c"= c(0,2,5,10)))
##
## Asymptotic Linear-by-Linear Association Test
##
## data: change2 by TRT_c (0 < 1 < 2 < 3)
## Z = -6.8141, p-value = 9.488e-12
## alternative hypothesis: two.sided
I*J 表(名義尺度*名義尺度)
条件付き
## I*J 表
x_i_j <- xtabs(formula = ~TRT_c + change3, data = th2)
x_i_j
## change3
## TRT_c -2 -1 1 2
## 0 8 33 7 2
## 1 5 23 18 4
## 2 0 14 28 8
## 3 1 7 21 21
cmh_test(x_i_j)
##
## Asymptotic Generalized Cochran-Mantel-Haenszel Test
##
## data: change3 by TRT_c (0, 1, 2, 3)
## chi-squared = 68.528, df = 9, p-value = 2.958e-11
I*J 表(順序尺度*順序尺度)
I*J 表でともに順序尺度のときはMantelの相関検定と呼ばれる。
chisq_test(x_i_j, scores = list("TRT_c"= c(1,2,3,4),
"change3"= c(1,2,3,4)))
##
## Asymptotic Linear-by-Linear Association Test
##
## data: change3 (ordered) by TRT_c (0 < 1 < 2 < 3)
## Z = 7.4665, p-value = 8.238e-14
## alternative hypothesis: two.sided
I*J 表(順序尺度*名義尺度)
片側の尺度のみにスコアを割り当てることも可能である。
chisq_test(x_i_j, scores = list("TRT_c"= c(1,2,3,4)))
##
## Asymptotic Generalized Pearson Chi-Squared Test
##
## data: change3 by TRT_c (0 < 1 < 2 < 3)
## chi-squared = 57.888, df = 3, p-value = 1.661e-12
サンプルサイズ計算
単群、対応のない2*2 表と対応のある2*2 表での割合の検定のサンプルサイズ計算のコード例を示す。
単群のサンプルサイズ計算
##単群のサンプルサイズ計算
OneSampleProportion.Equality(alpha=0.05, beta=0.2, p=0.8, differ=0.05)
## [1] 502.3283
対応のない2標本のサンプルサイズ計算
##対応のない2標本のサンプルサイズ計算
2 * TwoSampleProportion.Equality(alpha=.05, beta=0.2, p1=0.25, p2=0.15, k=1)
# 2 * power.prop.test(p1 = 0.15, p2 = 0.25, sig.level = 0.05, power = 0.8)[["n"]]
## [1] 494.4794
McNemar検定のサンプルサイズ計算
##McNemar検定(正規近似)のサンプルサイズ計算
p01 <- 0.15
p10 <- 0.45
n <- McNemar.Test(alpha=0.05, beta=0.2, p01/p10, p01+p10)
n
## [1] 49.90101
まとめ
計数データ(カテゴリカルデータ)について、二項分布、2*2表、I*J表の解析とサンプルサイズ計算を紹介した。特に2標本でのリスク比、オッズ比、リスク差は粗解析だけではなく、層別解析(Mantel-Haenzel推定量)、回帰分析による解析も行った。またI*J表の解析では、一般化Cochran-Mantel-Haenszel検定にとどまらず順序尺度へのスコアの割当も言及した。対応のあるデータの解析としては、McNemar検定とMcNemar-Bowker検定のコードを示した。もし本記事内で誤りを見つけられた方は、ご連絡頂ければ幸いである。
(メモ)今後、追加する可能性のある解析
- 拡張Mantel検定
- カッパ係数
サポートして頂けるとモチベーションに繋がりますのでぜひ宜しくお願いします。データ解析や臨床研究でのご相談があれば、お気軽にTwiiterもしくはメールにてご連絡下さい。
作成者:Masahiro Kondo
作成日:2022/3/4
連絡先:m.kondo1042(at)gmail.com
-
GLMがよくわからない場合は、 一般化線形モデル入門を読むとよい。 ↩︎


Discussion