CS50 Lecture5 Data Structure
配列
配列はメモリの塊が空の状態では存在しない

今の状態では3の隣に4を置けない
この状況では配列に数字を追加しないこともできるのか?
→ゴミのような値(オスカーの画像)の場所に4つ連ねて格納すれば良い
配列の唯一の定義はメモリが連続していなければならない
O(n) 値をコピーして新たな配列を作る作業があるので上限はO(n)になる
Ω(1) 配列はブラケット記法を使うことでワンステップで任意の場所に値を格納できる
Javaを書いたことがある人はわかるが、ベクトルはサイズを変更したり、大きくしたり小さくしたりできる配列のようなもの。
しかしC言語の配列はそうではない。C言語の配列は値が前後に並んだ連続したメモリのブロック。基本的には自分でサイズを変更しなければならない。
ポインタにより、データをつなぎ合わせていく。
ある意味で1次元の、次にある意味で2次元のデータ構造を非常に基本的な構成要素を使って作る。
下記の要素を使えば、配列よりもさらに洗練された独自データ構造を構築することができ、最終的には効率的に問題を解決することができるようになる。
struct 独自のデータ型
. 構造体の中に入って、nameやnumberを取得する方法としてドット演算子があった
* 間接参照演算子で特定のアドレスにいく
ドット演算子と、間接参照演算子の二つの演算子を組み合わせて、意図的に矢印のように見せる手法がよく使われる
→
ビルディングブロックのような連結リスト
配列の問題を解決する
配列の問題とは配列の問題とは
→ 配列を挿入するのに大きな0(n)ステップが必要なればそれは面倒だしコストもかかる
連結リスト
連結リストは元のデータを全て触って古い場所から新しい場所に移動させることなく、データ構造を大きくしたり小さくしたりできる

こんな感じで数字がテキトーな場所に置かれているとする(意図的に数字が分散されている)
→場所がテキトーだと探すのが大変
しかし、コンピュータのメモリを好きな場所に数字をかけるキャンバスのように考えることにすると、コンピュータのメモリに散らばっている他のものとは関係なく、1つ目、2つ目、3つ目となんとか辿り着ことができれば、それで良い。
1,2,3を格納するのに十分なメモリを使うのではなく、2倍の情報(少しのメタデータ)を格納してみる.
実際のデータを追跡するのに役立つ値。

2つ目のスペース(下に連結してるスペース)にはこれからリストと呼ぶもんお中の次の要素へのポインタを格納している。
0x0は全てのビットが0であることを示すが、これがnullと等価。
NULLはメモリに何か問題が発生したことや、スペースが足りないことを示す特別な記号。(アドレスがない状態)
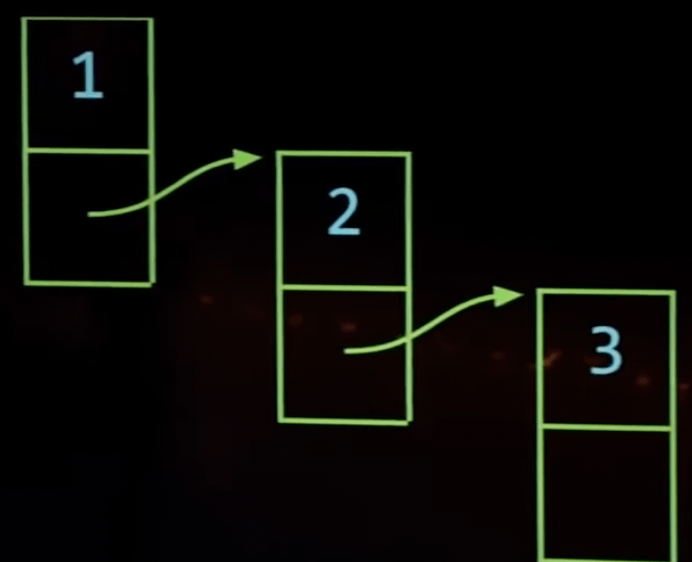
図式的には連結リストと呼ばれるこのデータ構造は、ポインタを解して接続さればいわばNODEと呼ばれるノード集合体である。
ノードとは、csの用語で、気になるものを格納するある種の構造。
ここで気にしているものは、数字と、他の構造体へのポインタ。
つまり、連結リストでこれらの長方形はそれぞれノードを表している。
最終的にC言語秒後の構造体と呼ばれるものを使って、ノードを実装する。
typedef struct node //struct nodeというものが存在するぞとヒントを与えている
{
int number;
//宣言したものを、データ構造の中で下記のようにして使うことできる
struct node *next;
}
node;//ここにnodeと書くことで、struct node でなく、nodeで呼び出せる
連結リストの割り当て
mallocを使って1つの構造体を動的に割り当て、その中に数字の1を入れ、別の構造体に数字の2を入れ、別の構造体に数字の3を入れる。
今、listと呼ばれる、何も指してないnullポインタがあるとすると、どのようにして1,2,3という3つの数字を持つ連結リストを割り当てれば良いか?


ポインタは何もさしていない。
リストと呼ばれる変数は、このリストがメモリのどこにあるかを追跡するためのもの

配列の世界では、新しいメモリの塊を割り当てて、この値を新しい値にコピーする必要があった。
連結リストの世界では、2回目にmallocを呼び出して、ノードが入るのに十分は大きさのメモリの塊をもう一つくださいというだけ。

これでサイズ2の連結リストができた
次に3を入れたい。
mallocは強力で、利用可能な場所であればどこからでもコンピュータのヒープ領域からメモリを取得できる。つまり、メモリは連続していない可能性がある。
次の数字は例えばコンピュータのメモリの中にあるとは限らない。
3回目にmallocを呼び出して3つ目のノードを割り当てた時、そのノードはコンピュータのメモリの離れた場所にあるかもしれない。(ポインタでつがってる)

この方法の欠点は二分探索に頼れないこと。 中身をO(n)より早くO(log n)で探すことができる。
一方、この方法の利点はサイズを変更するたびにメモリの割り当てとコピーを繰り返し、全ての値を変更する必要がないこと。
例えばtwitterやfacebookのようにデータが大量にあるものに関して、全てのデータをある場所から別の場所にコピーしなければならないということはパフォーマンス的には致命的。
生徒の質問: mallocはどこで使われていたのか?
回答: David先生が重たい木の箱(1,2など書かれているnode)を持ってきた時がmallocでメモリを確保していたということ。(malloc(1)とすることで、1のアドレスが返される)
上記の一連の流れを実際にコードに書くと下記のようになる
node *list = NULL;
//Davidがステージの外に出て、木の箱を持ってきたコードがこれ
//sizeofは言語の演算子でデータ型のサイズをなんバイトにするかを示すもの
//macやcs50 IDEでこれらのノードが何倍とを占めるのかを把握できる
node *n = malloc(sizeof(node));
mallocは1つの引数を取り、動的に割り当てたいバイト数を指定して、そのバイトの最初のアドレスを返す。
node *n = malloc(sizeof(node));
node *nには、nのアドレスを格納したい。
mallocはメモリを確保し、さらにその住所を返してくれるので、このコードで連結リストの次の値を増やすことができる。
また、C言語はいつでも、ポインタを返す関数を呼び出した時にはほとんど常にnullかnullでないかをチェックすべき。
もしnullだったら触るべきではない。
しかし、nullでなければ、メモリのどこかに有効なアドレスがあるということ。
if (n != NULL)
{
//*nでその住所に行く
//そのアドレスにある構造体の中のnumberにアクセスし、1を代入
(*n).number = 1;
}
上記のコードの後、まだやるべきことがある。
構造体の次のポインタを新たすゴミのような値をnullに置き換えたい。
(なぜ最初からlist→1に繋げないのかというと、mallocで利用可能なメモリを探し、その住所を一旦nに入れる。後からそれをそのままlistに入れる)
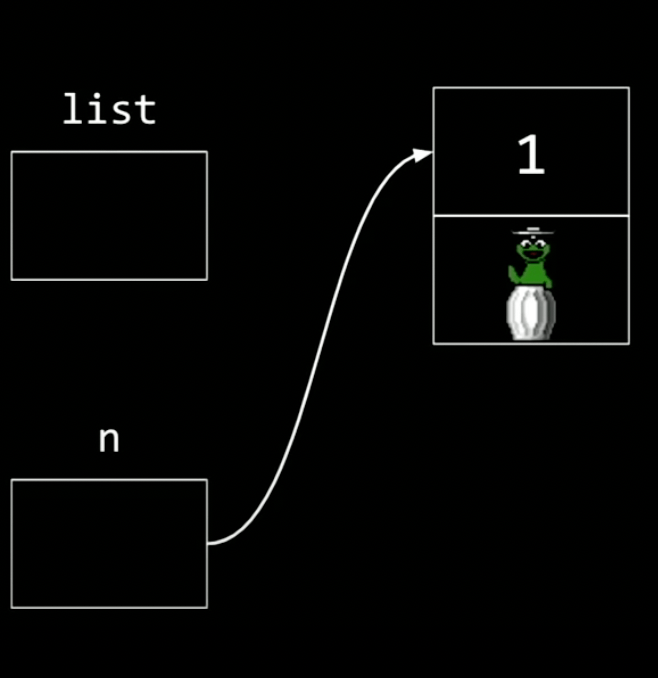
nullは不定で、これがリストの終わりであることを示す。それを実現するコードが下記
if(n != NULL)
{
//(*n).nextと同義
n->next = NULL;
}
アスタリスク、かっこ、ドットを矢印表記に置き換えることができる。
list = n;
(ここでlistに先ほどメモリを確保した連結リストの最初のアドレスがlistに格納できた。)
という1行のコードを実行して初めて、このノードがコンピュータメモリのどこにあるかを思い出す。
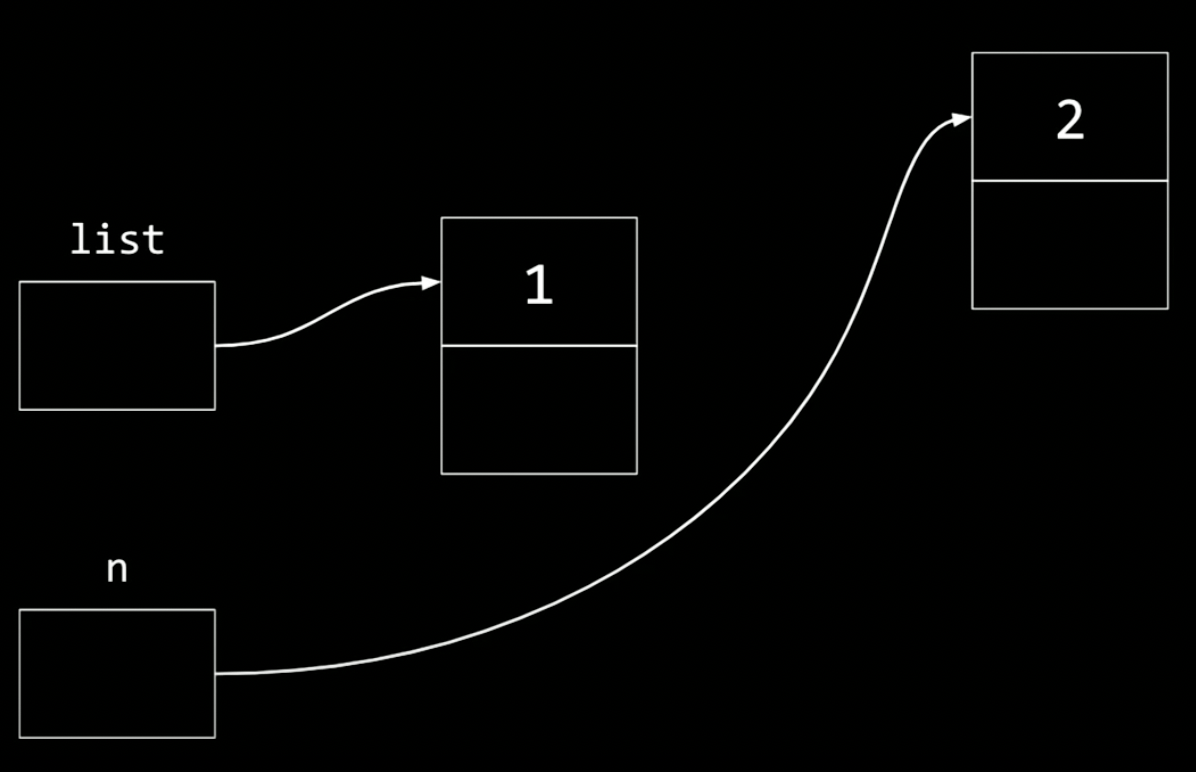
nextフィールド(領域)を更新して、新しく割り当てられたノードであるnを指すようにする。
そうすると図的にこうなる

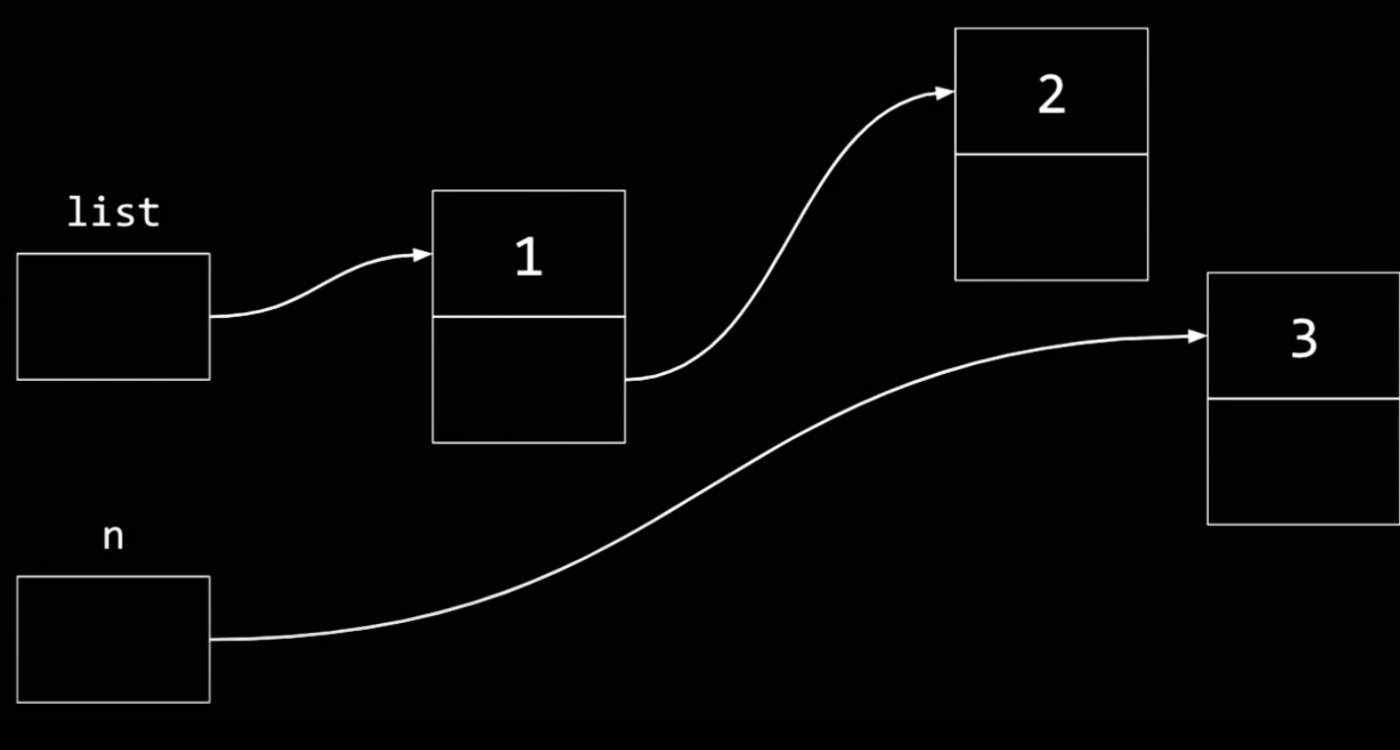
この連結リストに3番目のノードを挿入するには
、一時的な変数nがさすだけでなく、次のようにしなければならない。
list->next->next = n;
上記コードは下記によって説明できる。
もし、2を3にリンクさせたいなら、ここでリストから出発し、矢印に従ってすすむ。

そして、nextフィールドをnに設定する。
なぜならnは直近に割り当てられたノードの現在のアドレスだから。

現時点で図的にはこのようになっている
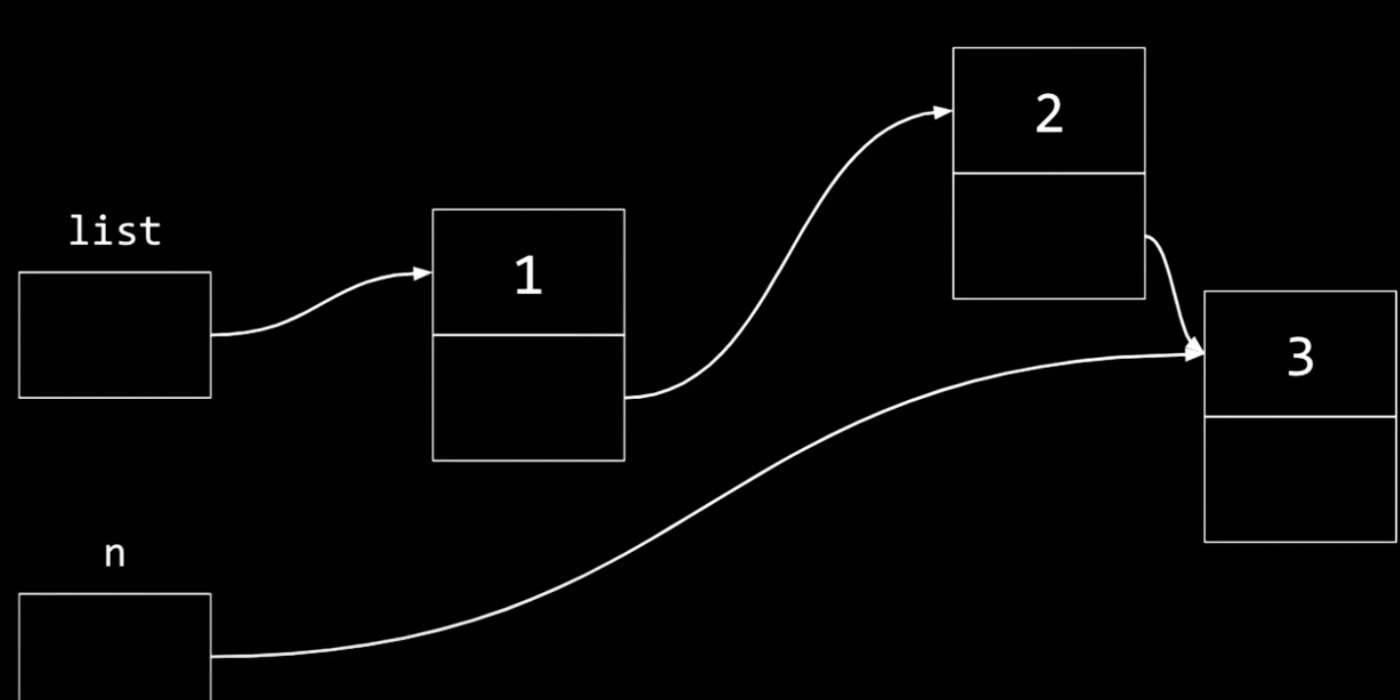
nは一時的な変数で、それを取り除けば、サイズ3の全く新しい連結リストを段階的に構築したことになる。
矢印を辿るのは一般的にはループを使うが、一時的な変数や、ループを適切に使えば、変数を何度も更新するだけで、ただ1本の矢印を書くことになる。
Q. 連結リストの検索にかかる時間は?
配列では、一定時間でリストの最後にジャンプできるが、連結リストはリストの最初のアドレスで示され、コンピュータはノードを一つずつしか確認できないので、検索にはO(n)がかかる
Q. 連結リストへの挿入にかかる時間は?
(アンケート結果がO(n)とO(1)に分かれる)
O(n)と回答した人の理由・・・mallocを使っても、最後の数字へ辿るために、listから1,2,3と辿っていかなければならないから
David先生の回答: 最後の数字は最後に来なければならないのでない。連結リストがソートされていなければならないという条件はないので、新しい数字をlistの次に入れることも可能。しかしソート順が犠牲になる。

なぜなら、mallocのステップがあるから。(矢印を抜いてまた接続する)
つまり、全部で3~4ステップ。
でも、4ステップというのも一定でステップ数が固定されているので、O(1)となる。
ソート順に拘らず、アルゴリズムやコードでソートを必要としないのであれば、それを回避して、一定時間での挿入を実現可能。
実際に数字を扱ったり、メモリ上のものを操作したりするプログラムをいくつか書いてみる。
普通に配列の中身を出力するコードが下記。
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
int list[3];
list[0] = 1;
list[1] = 2;
list[2] = 3;
for(int i = 0; i < 3; i++)
{
printf("%i\n", list[i]);
}
}
mallocによって返されたメモリの塊がある場合、ブラケット記法を利用して、配列として扱うことができる。
それは連続したメモリのブロックであり、まさにmallocが返すもの。
実際にそのアドレスに行って、そこに数字の1を置くこともできる。
そのアドレスに1を加えて、次の数字をそこに置くこともできる。
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//3つの整数を格納したければintの3倍を確保する
//動的に配列を確保してくれる
//配列を作るためのmallocの方法
//mallocは実際にそのサイズのメモリの連続した塊を返してくれるというもの
//前後に並べて返してくれる
int *list = malloc(3 *sizeof(int));
if(list == NULL)
{
return 1;
}
*list = 1;
//same list[0] =1;
*(list + 1) = 2;
*(list + 2) = 3;
}
しかしこれはポインタ演算子と呼ばれるもので、ポインタを使って演算を行うということは、今まで使ってきた構文、つまりブラケット記法を使うことと同じ。
ブラケット記法のメリットは、コンピュータが整数の大きさを知っているので、それぞれの整数の間隔を計算してくれること。
しかし、ここまでコードを書いて、「あ、4つ目に数字を入れたかったんだ」と思い出す。
この状態から書き直さず、どうやって動的に4つ目の位置に数字を入れるか?
ここで、一時的に別のメモリの塊を割り当ててみる。
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//3つの整数を格納したければintの3倍を確保する
//動的に配列を確保してくれる
//配列を作るためのmallocの方法
//mallocは実際にそのサイズのメモリの連続した塊を返してくれるというもの
//前後に並べて返してくれる
int *list = malloc(3 *sizeof(int));
if(list == NULL)
{
return 1;
}
*list = 1;
*(list + 1) = 2;
*(list + 2) = 3;
//一時的に別のメモリの塊を割り当ててみる
int *tmp = malloc(4 * sizeof(int));
if(tmp == NULL)
{
free(list);
return 1;
}
for(int i = 0; i < 3; i++)
{
//古い配列から新しい配列にコピー
tmp[i] = list[i];
}
//0からスタートした場合、4番目の位置になる。
tmp[3] = 4;
//ここまでの時点では、コピーされた元の配列位も1,2,3が入っており
//値が重複しているのでここで昔の配列の数字が入っているlistを解放する
//tmpに移したのでlilstはメモリ解放して良い
free(list);
//もとあった場所(list)に戻す
//新しいメモリの塊のアドレスを覚えておく
list = tmp;
//今度は4回目まで出力してみる
for(int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
}
**realloc・・・**メモリの割り当ての変更
3の配列から初めて、動的にそれを割り当て、サイズ4の新しい配列を作成してサイズを変更し、古い配列を新しい配列にコピーし、古い配列を開放して、以前のように処理を進める。
C言語では、ブラケット記法で配列を作成すると、窮地に追い込まれる。
→サイズを後から変更できないから。より技術的に言えば、ブラケット記法を使うと、スタック上に配列を静的に確保している事になる。コンピューターのメモリのうち、そのコンピューターに属するフレーム、つまり、その関数のスタックフレームに配列を入れている。
しかし、mallocを使って、「メモリの塊をくれ」といった場合、それはヒープからきている。そして、サイズ変更、メモをの返却、さらにもっと多くのメモリを取得することも可能。
しかし、実際にはもっと簡単な方法があり、メモリの塊のサイズを変更して再割り当てする場合、以前行っていたこのような作業(下記)を全て行う必要はない。
int *tmp = malloc(4 * sizeof(int));
if(tmp == NULL)
{
free(list);
return 1;
}
配列やメモリの塊サイズを変更して再割り当てする場合、以前行っていたような作業を全て行う必要はない。
mallocを2回使う必要はなく、最初に一回だけmallocを使えば良い。
そして、reallocで新しい関数を使うことができる。これによって、intのサイズの4倍のサイズのメモリの塊を再割り当てすることができる。
しかし、具体的にはリストと呼ばれるものを再割り当てする。
つまり、reallocはmallocとよく似ている。
しかし、二つの引数をもつ。
1つは欲しいメモリのサイズで、mallocと同じように既に割り当てたメモリの塊のアドレス。
reallocは賢く、既存のメモリの最後にたまたま空きがあった場合は、新しい適当なアドレスではなく、全く同じアドレスが返される。
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//3つの整数を格納したければintの3倍を確保する
//動的に配列を確保してくれる
//配列を作るためのmallocの方法
//mallocは実際にそのサイズのメモリの連続した塊を返してくれるというもの
//前後に並べて返してくれる
int *list = malloc(3 *sizeof(int));
if(list == NULL)
{
return 1;
}
*list = 1;
*(list + 1) = 2;
*(list + 2) = 3;
//ここにあなたがくれたのと同じアドレスがあります。
//サイズを変更してください
//サイズが4になるように再割り当てしてください
//さらに、古いものを新しいのにコピーしてくれる
int *tmp = realloc(list, 4*sizeof(int));
if(tmp == NULL)
{
free(list);
return 1;
}
//reallocのおかげで下記がいらなくなる
//for(int i = 0; i < 3; i++)
//{
// //古い配列から新しい配列にコピー
//tmp[i] = list[i];
//}
//0からスタートした場合、4番目の位置になる。
tmp[3] = 4;
//ここまでの時点では、コピーされた元の配列位も1,2,3が入っており
//値が重複しているのでここで昔の配列の数字が入っているlistを解放する
free(list);
//新しいメモリの塊のアドレスを覚えておく
//代入によって、変数名を再利用したことで、tmpを解放する必要はない
list = tmp;
//今度は4回目まで出力してみる
for(int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
free(list);
}
現在、手動でforループを使い、あるいはrealloc自身がforループを使って古い値を全て新しいattainいコピしなければならなかった。
これまでにかいたこのプログラムの3つのバージョンは全て0(n)だった。
挿入に関しては、連結リストのように重複せずに追加するというダイナミズムはなかった。
また、例えば構造体の先頭への挿入をO(1)の時間で行えるような機能はまだなかった。
単なる整数の配列ではなく、適切な連結リストとして実際に実装することが最終的な目標。
配列をソートしておけば検索がうまく行った。
O(log n)が得られる。
しかし、配列を動的に変更しようとすると、非常に高いコストになってしまう。
小さな配列の内容を新しい大きな配列にコピー非同期処理るにはO(n)のステップが必要になるかもしれない。全てのデータをコンピュータのメモリ上で常にコピーし続けたいとは思わない。
そこでポインタを使い、連結リストと呼ばれる構造体をつなぎ合わせることで、メモリの使用量は増えるが、それを回避することができるが、ソート順を犠牲にしなければならない。
事前に必要なノード数がわかっている場合に、ノードを割りあっててつなぎ合わせる作業を構文的に始めるためのビルディングブロックをいくつか見てみる。
初期化しないと、思いもよらぬ触ってはいけない 部分をしてしまうので、既知の値に初期化する。
実際にアドレスがない場合はnullを使用する。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(void)
{
//listというnodeの場所に行ってNULLを代入
node *list = NULL;
node *n = malloc(sizeof(node));
}
node *n = malloc(sizeof(node));
に関して、個々の整数を割り当てているのではなく、整数とノードへの別のポインタのための十分なスペースがある内部に、個々のノードを割り当てている。
また、sizeof演算子はmain上にある構造体の定義から、整数とstructへのポインタを格納するのに必要なスペースを算出している。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(void)
{
//listというnodeの場所に行ってNULLを代入
node *list = NULL;
//確保したノードのアドレスをnに入れる
node *n = malloc(sizeof(node));
if(n == NULL)
{
return 1;
}
n->number = 1;
n->next = NULL;
//nはノードのアドレスなのでそのまま代入
list = n;
}
これまで同様、もしnがNULLの場合、プログラムから抜け出し、1を返す。
何かが間違っていて、メモリが不足しているから。
しかし、全てがうまく行った場合は、先に進んでノードnに行き、そのnumberフィールドに行って値1を割り当てる。
また、ノードnのnextフィールドに入り、とりあえずnullという値を割り当てておく。
listという変数は、リスト全体を表す変数。
そして、実際のノードを指すようになったので、ノードへのポインタであるlistに、実際のノードのアドレスであるnに等しい値を設定する。
この時点では、小さな木のブロックが、1を含む大きなブロックに接続されている。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(void)
{
//listというnodeの場所に行ってNULLを代入
node *list = NULL;
//main上の構造体nodeの定義からnumberとnextを入れるのに必要なスペースを算出
node *n = malloc(sizeof(node));
if(n == NULL)
{
return 1;
}
n->number = 1;
n->next = NULL;
list = n;
n = malloc(sizeof(node));
if(n == NULL)
{
//メモリリークしないように先にlistを解放する
free(list);
return 1;
}
n->number = 2;
n->next = NULL;
//(*list).next = n;
list->next = n;
}
今度は整数だけではなくノードを使って、数字の2をこのリストに追加してみる。
ノードnに入り、そのnumberフィールドに2という数字を格納する。
そしてそのノードはソートされた状態で挿入されているので、nextにはNULLを挿入する。
もし本当に1番のノードの後に2番のノードを置きたいのであれば、リストの一番上から初めて、nextノードにいく。
そして、その値にnを代入する。
小さなブロックから始まり、矢印にしたがって、最初のノードである1番目のノードのnextポインタを更新して、代わりにこの新しいノードのアドレス、nを格納する。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(void)
{
node *list = NULL;
node *n = malloc(sizeof(node));
if(n == NULL)
{
return 1;
}
//(*n).number = 1;と同義
n->number = 1;
n->next = NULL;
//nには最初に取得したnodeのアドレスが格納されており、それをそのままlistに代入
list = n;
n = malloc(sizeof(node));
if(n == NULL)
{
//メモリリークしないように先にlistを解放する
free(list);
return 1;
}
n->number = 2;
n->next = NULL;
list->next = n;
n = malloc(sizeof(node));
if(n == NULL)
{
//メモリリークしないように先にlistを解放する
free(list->next);
free(list);
return 1;
}
n->number = 3;
n->next = NULL;
//矢印を辿ってる
//この表記はあまり良くなくて、for文を使った方が良い
list->next->next = n;
//一時的な変数 = listが初期値。
//tmpがNULLでなければ、tmpのnextの値を代入していく
//tmp->nextは(*tmp).nextと同義
for(node *tmp = list; tmp != NULL ; tmp = tmp->next)
{
//次のフィールドを更新していく
//ブロックリストの端から矢印が切れて、NULL(0x0)を指すようになるまで続ける
printf("%i\n", tmp->number);
}
//連結リストを解放する
while (list != NULL)
{
//一時的にtmpという変数をくれと言ってる
//listノードのnextをどんどんtmpに入れていく
//tmpはポインタ
//最初のノードではなく、次のノードを代入してる
node *tmp = list->next;
//リスト(連結リストの最初ノード・全体ではない )自体を解放できる
//現在のノードだけを解放するようなもの
free(list);
//後続のリストを再度listに代入し、while分を回して繰り返す
list = tmp;
//lisがなくなったら終了(全てメモリが解放される)
//一時変数を使って一歩先を守ることで、メモリをすぐに解放しすぎて皇族のノードにアクセスできなくなってしまうことがないようにしている
}
}
配列 動的に割り当てられた配列 連結リスト
Q. なぜmallocを使って一気にメモリを確保せず、連結リストを使うのか?
A. 配列はメモリの塊。順番にメモリに格納しなければならないが、実際配列に何かを格納するとき、 一番めと二番めの間、二番めと三番めの間には時間が空いたり、他のメモリが入ったりする。そのような場合に連結リストが有効になる。

この状態の連結リストの間にnodeを追加してみる
node *n = malloc(sizeof(node));
if(n != NULL)
{
n->number = 1;
n->next = NULL;
}
と言うコードでnodeだけ確保し、まだ連結はさせていない状態
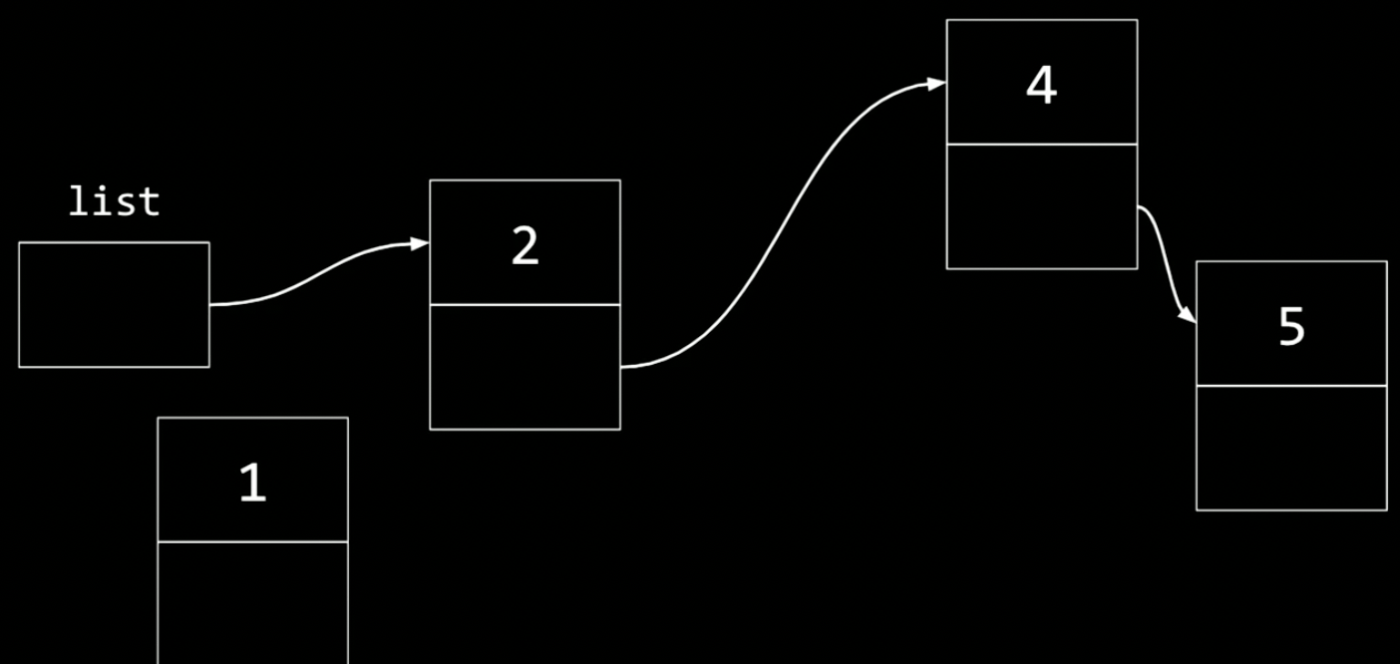
図に表すとこの状態になっていると言うこと
直感的にもし、1が2よりも先にあったら



listから2に繋がっていた矢印を1に繋いで。list = 2だったのをlist = 1にしてしまえばいいと考えるが、
2以降の連結リストがメモリのどこにあるかわからなくなってしまう。
なので、2のアドレスをどこかにメモしておかなければならない。
そうでなければ、大規模なメモリリークが発生してしまうため、順序が重要。
だから、最初にやるべきこととして、1の矢印は次は2に向けるべき

次にlistの矢印を1に向けることができる

だから、最初に書いた下記のコードのように
node *n = malloc(sizeof(node));
if(n != NULL)
{
n->number = 1;
//①
n->next = list;
//②
list = n;
}
①新たに追加するノードの次の矢印は、現在のlistにあるものを指さなければならない。
②リストが新しいノードを指すように更新
連結リストは、配列のように途中の値に直接アクセすることはできない、一次元的な情報。
また、二分探索ではソートされていれば、素早く検索することを可能にするものだった。
ここで、配列を、長さだけでなく、高さもある2次元の構造だと考える
ツリー
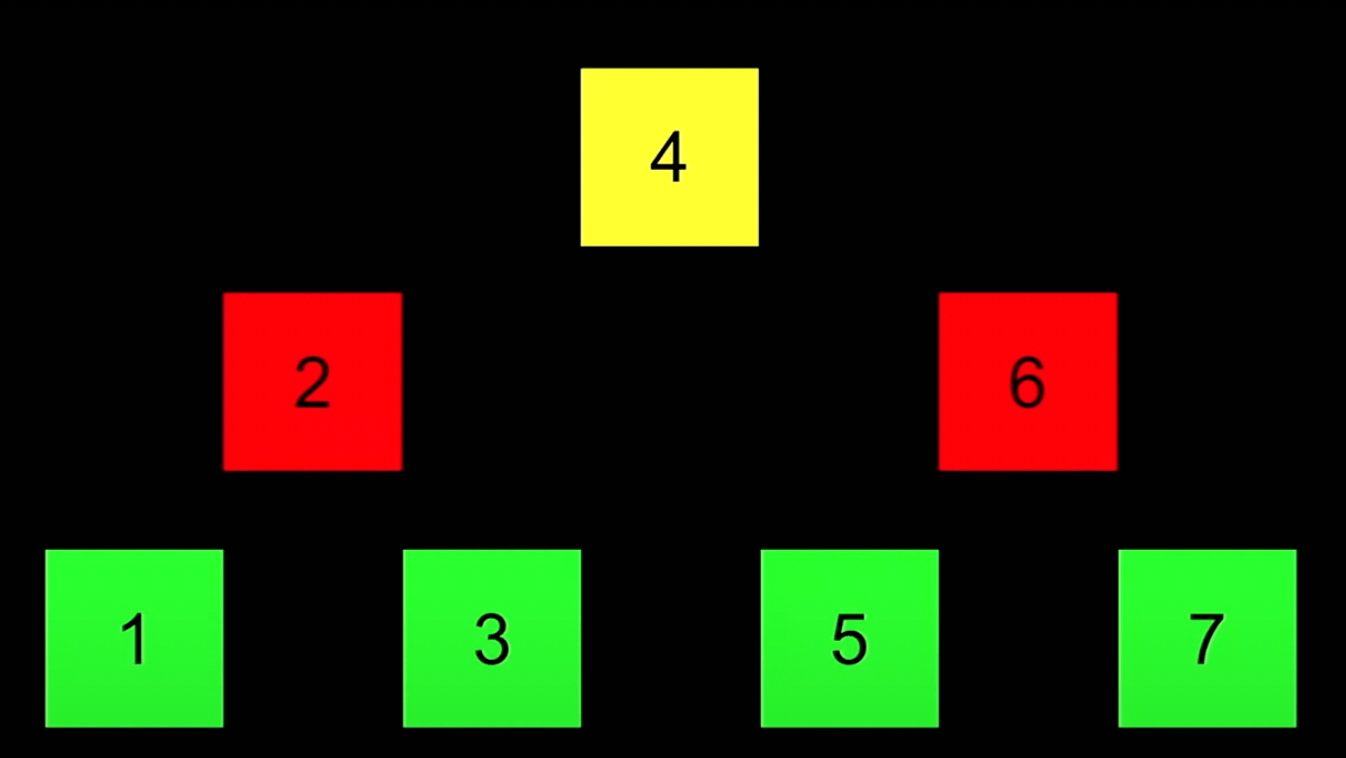
しかしこれらを何で繋げば良いか?
→ポインタで繋ぐ

この構造で,連結リストでも二分探索ができるようになる。
上記を実装するコード
typedef struct node
{
int number
struct node *left;
struct node *right;
}
node;
これで、左を指せば、より小さなサブツリー、右を指せば、より大きなサブツリーを指すことができる。
C言語で「ツリーから数字を検索する」と言う目的の関数を宣言すると、定義上ツリーのルートから下に向かって検索することになる。
bool search(/*①*/node *tree, /*②*/int number)
{
//探していて何もない場合はNULL
if(tree == NULL)
{
return false;
}
else if(number < /*③*/tree->number)
{
return search(tree->left, number);
}
else if(number > tree->number)
{
return search(tree->right, number);
}
else/* ここはいらない if(number == tree->number)*/
{
return true;
}
}
①nodeへのポインタ(ツリー)(ルート)
また、*treeなので、実際のtreeのアドレスに入っている
②4,6,8など気になる数字を受け取る
③実際のtreeのnumberを確認している
それ以降も、2つのサブツリーに新しいルートノードを加えたもの。
nがtreeの総数だとすると、log₂nが木の高さになる
(3 = log₂8)
挿入の実行時間は新しい数字が続数場所を見つけるのに何ステップかかるかに相当する。
バランスの取れた二分探索木への挿入はO(log₂n) になる
挿入や削除の際にツリーのバランスを保つために必要に応じて物事をシフトさせるアルゴリズムが組み込まれている(ALV木や赤黒木など)
ハッシュテーブル
ここで、配列や連結リストを組み合わせたもの
検索と挿入に要する時間がO(1)になる
26の配列
今格納したいデータが数字ではなく、辞書や連絡先や名前だとする
0番目にA25番目にZがあるとする。
この通り名前を追加していく際、名前の頭文字が同じアルファベット(ハーマイオニーハリーはグリッド)の場合はどうすれば良いか?

input → □ → output
問題解決そのものと、機能とは何かを考えれば良い
input(char*) → [hash function]→ output(int(0~25))
ASCIIが文字列を数字にしてくれるので、65を引けば0~25の数字にできる
縦に並んでいるアルファベットの列を、3文字まで縦で並べる。
すると、3人の名前を一度で挿入することができる
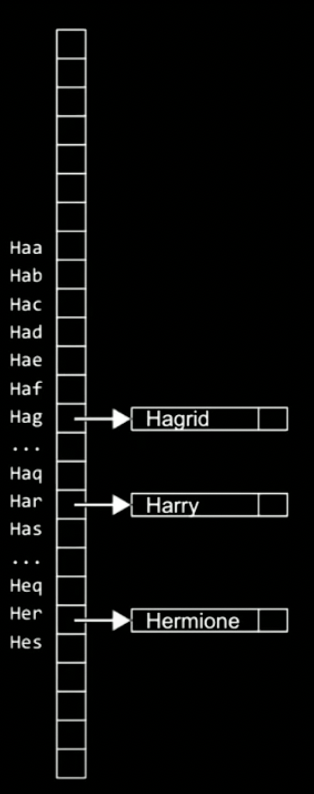
この方法は262626=17576のメモリを使うことになるが、問題は必要なメモリが増えることではなく、使わないメモリが生まれること。
しかし、各括弧表記を使って演算できるように、それらが存在しなければならない
ハッシュ化とはある入力を見て、その入力の特徴(カードのスーツや、アルファベットの文字)に基づいて、バケツの0,1,2,3のような数値を出力すること
ハッシュテーブルを使うと、入力をバケツかでき、より素早くデータにアクセスできる。
(ダイヤのAを探したいならば、52枚の中から探すのではなく、ダイヤの13枚の中から探せば良い)
ハッシュテーブルの検索にかかる時間はどうなるか?
O(処理にかかる最長の時間)やΩ(処理にかかる最短時間)を考える場合は、÷4や×2などの定数は取り除いて考える。
なので、ハッシュテーブル検索は0(n)である
trie(データ構造)
プリフィックスツリーとも呼ばれる。
数字だけでなく、単語やその他のより高度なデータを格納するために使用される。
下記はtrieのノードで、長方形や正方形のような意味でのノード。そのノードの内部にはこの場合、サイズ26の文字通りの配列がある。
trieとは木のことで、各ノードが配列になっている。
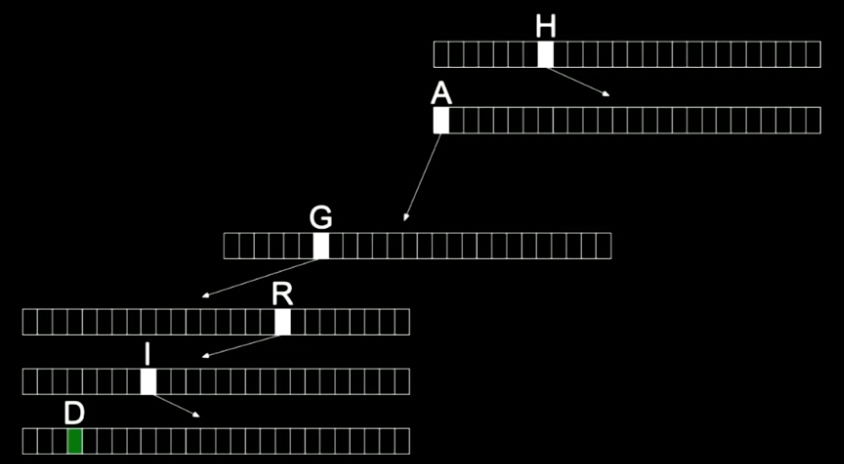
その配列はそれぞれ他のノード(A~Zまで持っている配列)へのポインタへの配列。
ハグリッドを探したい場合は、Hのポインタ、Aのポインタ、Gのポインタ...というようにたどっていく。
この構造体の中にはブールちがあり、「yes」か「no」ではグリッドが連絡先にいるか否かを示す。緑は 「yes」を表しているので、H・G・R・I・Dは連絡先に存在するということになる。
HARRYとHAGRIDはこのように表される

HAGRIDを探すのに何ステップかかるか?
→6ステップ(文字列分)
少なくとも人間の名前の長さ分だけの一定の時間がかかる。
trieデータ構造にどれだけ多くの名前を詰め込んでも、人間の名前の文字数分しかかからず、データ量は探すステップすうに影響しない。
だから、trie構造はO(1)も可能。
しかし、大量のNULL(0x0)(8bit)を格納してメモリを無駄遣いしているので遅くなる。
配列の最も重要な特性は全てが連続しているということ。全てのノードにサイズ26の配列を配置するとなると、大量おメモリを消費しなければならなくなる。
この種のデータ構造で他に何ができるか?
配列は最も単純なデータ構造。配列はそれ自体は構造体でもなく、ただの連続したメモリの塊。
連結リストは1次元のデータ構造で、ノードとメモリをつなぎ合わせることができ、動的な割り当てが可能。
ツリーは配列と連結リストの両方の長所を兼ね備えていた。
ハッシュテーブルは配列と連結リストの2つのアイデアが融合した。
trieは一見するとより良いように見えるが、大きなコスト(メモリを無駄遣いしてしまう)がかかる。
そこで、これらのビルディングブロックを自由に使えるようにすると、より高いレベルの問題を解決するために低レベルの実装の詳細として実際に使用できることがわかった。
小rが、抽象データ構造。
これは現実世界の問題を実装するために思い浮かべる心の中の構造のようなもので、通常は他のデータ構造で実装されている。
どの世なものがあるか?
queues
待ち行列は非常に一般的な抽象データ構造。
イギリスで育った人は、お店の外に並んでいる列をキューと呼ぶ。
自分が最初に並んだら、最初に抜けられる特徴。
そこで、待ち行列が正しく実装されていれば、FIFO(先入先出し)と呼ばれる性質を持っている。
二つの性質を持っている
追加や削除、挿入や削除などなんとでも呼べる。
enqueue・・・お店に行って列に並ぶ
dequeue・・・自分の番になり、店の中に案内される
配列の問題点は最初の何人かをデキュー(店内に案内)したら列の先頭に空きスペースがあること。
しかし、最後の人にはまだ新しい人を入れるスペースがない。
デキューした分移動させるとすると、0(n)となるがこれは理想的ではない。
連結リストであれば、どんどん人を追加がすることができる。
stacks
配列や連結リストを使って実装できるデータ構造。
後入れ先出し。LIFO。
後に積み上げたものが先に取り出される。
追加削除挿入削除と同じこと。
push
pop
dictionaries
配列や連結リスト、ハッシュテーブル、tireなどで実装でき、キーと値を関連づけることができる抽象的なデータ型。
辞書には定義があり、アルファベット毎に並んでいる。キーと辞書は、値を関連づける抽象的なデータ型。
単語の定義を調べると気にその単語自体を調べるように、キーを使って値を調べる。
Discussion