Juliaで有限要素解析をする(Gridap.jl)
はじめに
この記事はJulia AdventCalendar 2023 12/23日分の記事となります。
どうも、Marieと申します。
この記事では、有限要素解析を解くためのjuliaのライブラリ、Gridap.jlを使ってみた話をします。
今回は弾性体の静的解析を例にしていきます。
準備:材料パラメータの設定
Gridap.jlとは関係ないですが必要なものを記述しておきます。今回はGridap.jl Tutorial準拠で鉄のパラメータを使用します。
const E = 70.0e9
const ν = 0.33
const λ = (E*ν)/((1+ν)*(1-2*ν))
const μ = E/(2*(1+ν))
σ(ε) = λ*tr(ε)*one(ε) + 2*μ*ε
ラメ定数を使ってひずみと応力の関係性の式を定義しておきます。
モデルの入力
Tutorialにおいてはjson形式の入力とオイラー座標で自分で定義したものを紹介しています。
その他にもGridapGmshを使うことで、Gmshを使ってメッシュ割したものを読み込むことができます。
using Gridap
model = DiscreteModelFromFile("model.json")
using Gridap
using GridapGmsh
model = GmshDiscreteModel("model.msh")
using Gridap
domain2d = (0,1,0,1) # 範囲
partition2d = (20,20) # 分割点の量
model2d = CartesianDiscreteModel(domain2d,partition2d)
# 3次元でも同様にタプルを置くことで、定義できる。
# domain3d = (0,1,0,1,0,1)
# partition3d = (20,20,20)
# model3d = CartesianDiscreteModel(domain3d,partition3d)
今回は簡単のために、オイラー座標系で定義したものを使用します。
モデル、結果の出力
一旦どのようにモデルが定義されているかParaviewを使ってみてみましょう。
writevtk(model2d,"result/model")
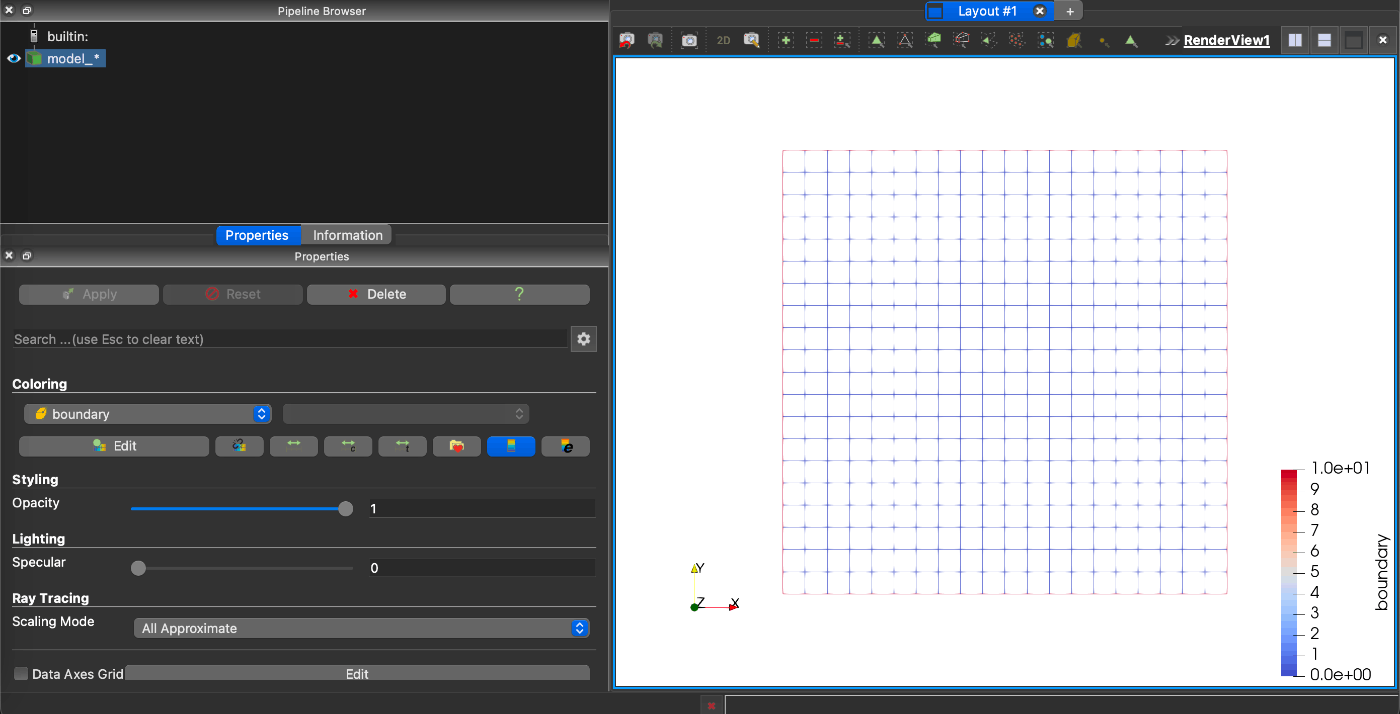
定義したように20x20に分割された平面が定義されていることがわかります。
また、モデルを出力すると、boundaryやentityなどいくつか座標がラベル付けされています。勝手にラベル付することはCartesianDiscreteModel()特有なのですが、gmshなどで事前にラベリングしたラベルもここで取り込まれます。
このようなラベルは後々境界条件や物性パラメータを割り振る際に役立ちます。
ラベルの追加
ラベルを後々追加することもできます。この時に渡す引数はtag_nのindexと同じものを指定してあげるとうまくいきます。ここでは左側の辺を固定して、右側の辺へ強制変位をかけたいので、以下のように記述していきます。
labels = get_face_labeling(model2d)
add_tag_from_tags!(labels,"fix",[1,3,7])
add_tag_from_tags!(labels,"deform",[2,4,8])
有限要素の構築
次に、有限要素空間を構築して、境界条件を結びつけていきます。
ここでは1次のlagrange補完によって形状関数を作ってあげて、そこから境界条件や強制変位条件を先ほど定義したラベルの地点へと結びつけています。
今回は右辺に1%のひずみを加えることとしました。
reffe = ReferenceFE(lagrangian,VectorValue{2,Float64},order)
V0 = TestFESpace(model2d,reffe,conformity=:H1,dirichlet_tags=["fix", "deform"])
f1(x) = VectorValue(0.0, 0.0)
f2(x) = VectorValue(0.01, 0.0)
U = TrialFESpace(V0,[f1, f2])
ここで、ReferenceFEのVectorValueの数は境界条件の結びたい条件数と揃える必要があります。
解きたい弱形式の設定
今回はGridap.jl Tutorialを参考にして弱形式
に対して外力が0の条件を解いていきます。
degree = 2
Ω = Triangulation(model2d)
dΩ = Measure(Ω,degree)
a(u,v) = ∫( ε(v)⊙(σ∘ε(u)) )*dΩ
l(v) = 0
Gridap.jlでは、σ∘ε(u)は合成関数です。
ソルバーの設定、結果の確認
では準備が整ったので、問題を解いていきましょう。
op = AffineFEOperator(a,l,U,V0)
uh = solve(op)
writevtk(Ω,"result/results",cellfields=["uh"=>uh,"epsi"=>ε(uh),"sigma"=>σ∘ε(uh)])

うまく計算されてそうな結果を確認することができました。
最後に
扱いが少し難しいですが、楽しいので是非に遊んでみてください。最近はchatGPTを使って英語を読み解くこともかなり楽で、Juliaは軒並みTutorialがしっかりしているので公式ドキュメントの海を漁ってみるといいかもしれないです。
(非線形な偏微分方程式も解けるので、超弾性や流体にも対応してます。)
また、間違っていたりなどありましたらコメントください......(当方非専門謝罪......)
参考文献
・Gridap.jl Tutorials(https://gridap.github.io/Tutorials/dev/)
・Gridap.jl Documentation(https://gridap.github.io/Gridap.jl/dev/)
Discussion