【Julia】Agents.jlを利用したマルチエージェントシミュレーション②連続空間での感染症拡大
はじめに
今回はAgents.jlの連続空間における感染症拡大例題について見ていきます。例題では物理の運動方程式を利用してモデルを構築しています。
▼URL
▼関連
連続空間で動くagent
using Agents, Random
mutable struct Agent <: AbstractAgent
id::Int
pos::NTuple{2,Float64}
vel::NTuple{2,Float64}
mass::Float64
end
連続空間においてagentはpos=座標位置情報と、vel=速度情報を扱う浮動小数点型のタプルを用意します。また、massは質量を扱います。後に運動方程式を用い、動かないagentを用意するためです。
function ball_model(; speed = 0.002)
space2d = ContinuousSpace((1, 1), 0.02)
model = ABM(Agent, space2d, properties = Dict(:dt => 1.0), rng = MersenneTwister(42))
# And add some agents to the model
for ind in 1:500
pos = Tuple(rand(model.rng, 2))
vel = sincos(2π * rand(model.rng)) .* speed
add_agent!(pos, model, vel, 1.0)
end
return model
end
model = ball_model()
ball_model関数でABMを生成できるようにします。ボールが空間内を動き回る様子だけをまずは作ります。
0-1範囲の平面空間とmodelを定義し、500体のagentを作り出します。pos(座標)とvel(速度ベクトル)はランダムで、add_agent!関数により各agentのpos, vel, mass(=1.0)にそれぞれ値が入るようにします。
agent_step!(agent, model) = move_agent!(agent, model, model.dt)
連続空間においてmove_agent!関数が用意されていてこれを利用します。
using InteractiveDynamics
using CairoMakie
abm_video(
"socialdist1.gif",
model,
agent_step!;
title = "Ball Model",
frames = 50,
spf = 2,
framerate = 25,
)
# jupyter notebook上で見るためにgif形式
display("image/gif", read("socialdist1.gif"))
可視化ライブラリを用いて、agentが連続空間を動くだけのシンプルなABMが見られます。
agent同士の衝突
function model_step!(model)
for (a1, a2) in interacting_pairs(model, 0.012, :nearest)
elastic_collision!(a1, a2, :mass)
end
end
model2 = ball_model()
abm_video(
"socialdist2.gif",
model2,
agent_step!,
model_step!;
title = "Billiard-like",
frames = 50,
spf = 2,
framerate = 25,
)
display("image/gif", read("socialdist2.gif"))
interacting_pairsメソッドを利用し、0.012以内の最も近い距離にいるagentを取得します。そしてelastic_collision!メソッドを用いて、該当の2体のagentを衝突させます。(わざわざ自力で衝突後のvelを更新する計算式を書かなくてもこのように用意されているものを利用できるので便利ですね。)
動かないagent
model3 = ball_model()
for id in 1:400
agent = model3[id]
agent.mass = Inf
agent.vel = (0.0, 0.0)
end
abm_video(
"socialdist3.gif",
model3,
agent_step!,
model_step!;
title = "Billiard-like with stationary agents",
frames = 50,
spf = 2,
framerate = 25,
)
display("image/gif", read("socialdist3.gif"))
idが1~400までの400体のagentのmassを無限大にし、velをゼロにします。
感染拡大(SIRモデル)の追加
SIRモデルは古典的な感染症拡大のモデルであり、
S:susceptible(未感染者)
I:infected(感染者)
R:recovered(回復者)
を表します。ABMではこれらの状態を各agentに与え、SとIが近くに居たらある確率で感染が起こり(S→Iに変化)、Iのagentは一定時間後回復する(I→R)ような現象を構築していきます。
mutable struct PoorSoul <: AbstractAgent
id::Int
pos::NTuple{2,Float64}
vel::NTuple{2,Float64}
mass::Float64
days_infected::Int # number of days since is infected
status::Symbol # :S, :I or :R
β::Float64
end
boll_modelでのagentに加えて、感染日数と感染状態、βを与えます。βは感染確率です。agentに与えることで個々人のagentの免疫力によって感染が起きるか起きないかを表現する狙いがあります。
const steps_per_day = 24
using DrWatson: @dict
function sir_initiation(;
infection_period = 30 * steps_per_day,
detection_time = 14 * steps_per_day,
reinfection_probability = 0.05,
isolated = 0.0, # in percentage
interaction_radius = 0.012,
dt = 1.0,
speed = 0.002,
death_rate = 0.044, # from website of WHO
N = 1000,
initial_infected = 5,
seed = 42,
βmin = 0.4,
βmax = 0.8,
)
properties = @dict(
infection_period,
reinfection_probability,
detection_time,
death_rate,
interaction_radius,
dt,
)
space = ContinuousSpace((1,1), 0.02)
model = ABM(PoorSoul, space, properties = properties, rng = MersenneTwister(seed))
# Add initial individuals
for ind in 1:N
pos = Tuple(rand(model.rng, 2))
status = ind ≤ N - initial_infected ? :S : :I
isisolated = ind ≤ isolated * N
mass = isisolated ? Inf : 1.0
vel = isisolated ? (0.0, 0.0) : sincos(2π * rand(model.rng)) .* speed
# very high transmission probability
# we are modelling close encounters after all
β = (βmax - βmin) * rand(model.rng) + βmin
add_agent!(pos, model, vel, mass, 0, status, β)
end
return model
end
細かいパラメータがたくさん出てきますが、意味は大体英語の通りです。これらのパラメータは後に感染条件を記述する際に用います。初期agentを1000体生成し、5体の初期感染者を置きます。
sir_model = sir_initiation()
sir_colors(a) = a.status == :S ? "#2b2b33" : a.status == :I ? "#bf2642" : "#338c54"
fig, abmstepper = abm_plot(sir_model; ac = sir_colors)
fig # display figure

sir_modelを作り、各agentのstatusに応じて色を変えます。初期画面を出力しています。
function transmit!(a1, a2, rp)
# for transmission, only 1 can have the disease (otherwise nothing happens)
count(a.status == :I for a in (a1, a2)) ≠ 1 && return
infected, healthy = a1.status == :I ? (a1, a2) : (a2, a1)
rand(model.rng) > infected.β && return
if healthy.status == :R
rand(model.rng) > rp && return
end
healthy.status = :I
end
function sir_model_step!(model)
r = model.interaction_radius
for (a1, a2) in interacting_pairs(model, r, :nearest)
transmit!(a1, a2, model.reinfection_probability)
elastic_collision!(a1, a2, :mass)
end
end
sirの状態を更新するためのステップ関数を記述します。transmit関数では、2体のagentを引数に取り、以下の感染条件を記述しています。(かなり省略されてスマートに条件分岐が記述されているので、読解がやや難しいです)
①片方のみI
②Iじゃない方のagentの感染確率を満たす
③Iじゃない方のagentがRだった場合、再感染確率でIに変わる(感染する)
④Iじゃない方のagentがSだった場合、Iに変わる
sir_model_step関数は、相互作用が起きる範囲内において最も距離が近い2体のagentを取得し、これをtransmit関数に渡しています。また、よりランダムな動きを表現するために衝突も定義されています。
function sir_agent_step!(agent, model)
move_agent!(agent, model, model.dt)
update!(agent)
recover_or_die!(agent, model)
end
update!(agent) = agent.status == :I && (agent.days_infected += 1)
function recover_or_die!(agent, model)
if agent.days_infected ≥ model.infection_period
if rand(model.rng) ≤ model.death_rate
kill_agent!(agent, model)
else
agent.status = :R
agent.days_infected = 0
end
end
end
sir_agent_step関数はstatusのsirの更新以外の項目に関するステップ関数になります。update!関数は、感染日数を更新する関数です。recover_or_die!関数はその名の通り、agentの感染日数が指定の日数に到達したら、指定の死亡率に従ってkill_agent!(該当agent自体がmodel中から削除されます。なので合計agent数は減ります)され、生き延びたagentのstatusはRに変わります。
sir_model = sir_initiation()
abm_video(
"socialdist4.gif",
sir_model,
sir_agent_step!,
sir_model_step!;
title = "SIR model",
frames = 100,
ac = sir_colors,
as = 10,
spf = 1,
framerate = 20,
)
display("image/gif", read("socialdist4.gif"))
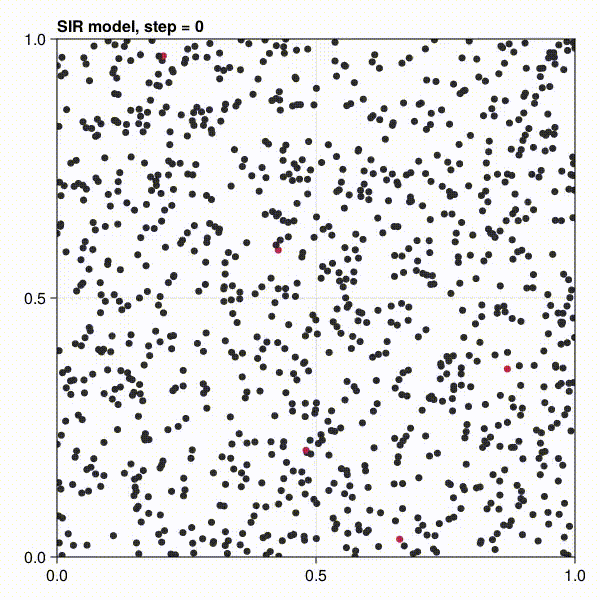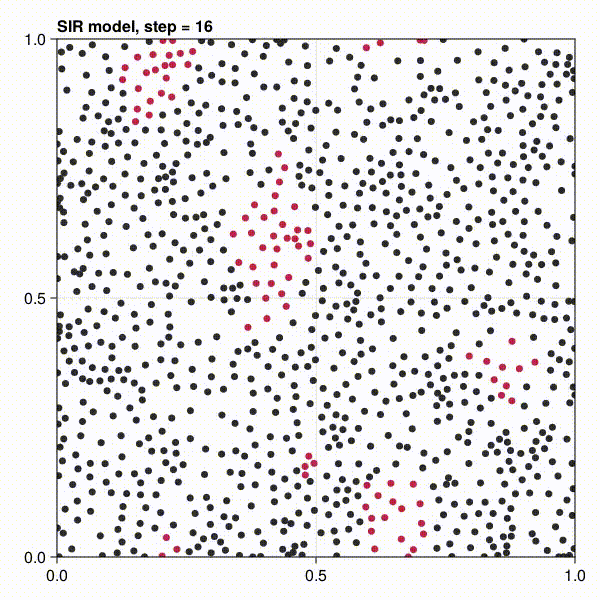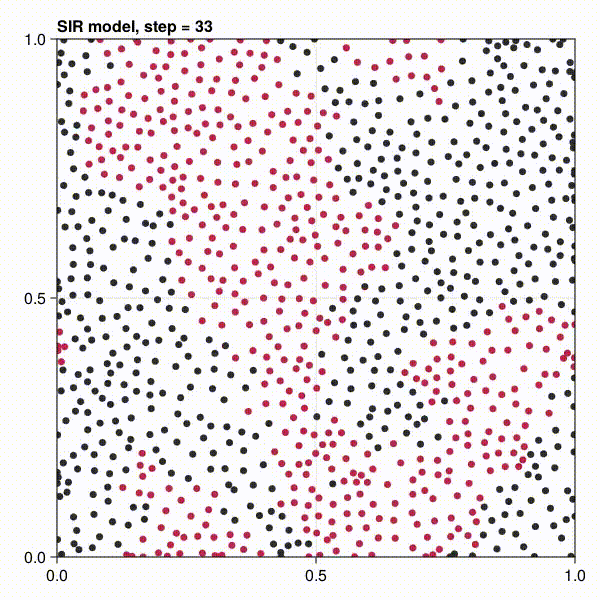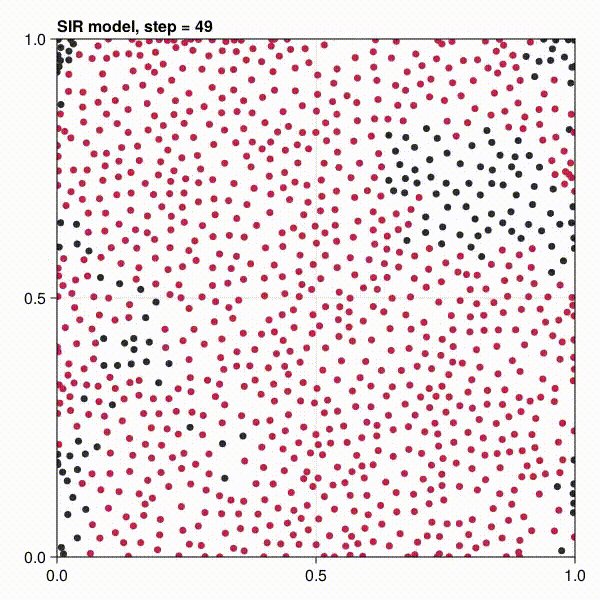
感染したagentが赤くなっていくことが分かると思います。
爆発的な感染
infected(x) = count(i == :I for i in x)
recovered(x) = count(i == :R for i in x)
adata = [(:status, infected), (:status, recovered)]
sirそれぞれのstatusを持っているagentの数をstepごとにadata(dataframe)に格納していきます。
r1, r2 = 0.04, 0.33
β1, β2 = 0.5, 0.1
sir_model1 = sir_initiation(reinfection_probability = r1, βmin = β1)
sir_model2 = sir_initiation(reinfection_probability = r2, βmin = β1)
sir_model3 = sir_initiation(reinfection_probability = r1, βmin = β2)
data1, _ = run!(sir_model1, sir_agent_step!, sir_model_step!, 2000; adata)
data2, _ = run!(sir_model2, sir_agent_step!, sir_model_step!, 2000; adata)
data3, _ = run!(sir_model3, sir_agent_step!, sir_model_step!, 2000; adata)
data1[(end-10):end, :]
感染率に関わるパラメータを変え、シミュレーションを実行します。
using CairoMakie
figure = Figure()
ax = figure[1, 1] = Axis(figure; ylabel = "Infected")
l1 = lines!(ax, data1[:, dataname((:status, infected))], color = :orange)
l2 = lines!(ax, data2[:, dataname((:status, infected))], color = :blue)
l3 = lines!(ax, data3[:, dataname((:status, infected))], color = :green)
figure[1, 2] =
Legend(figure, [l1, l2, l3], ["r=$r1, beta=$β1", "r=$r2, beta=$β1", "r=$r1, beta=$β2"])
figure

感染者の人数を各パラメータごとに出力します。いずれのケースにおいても、爆発的な感染増加になります。
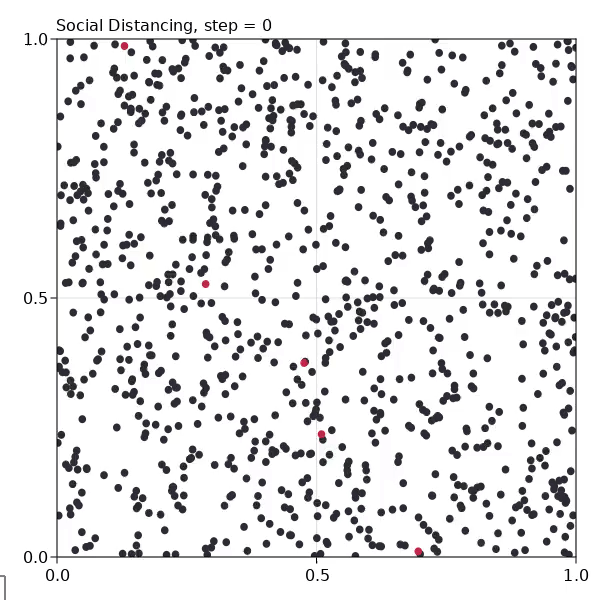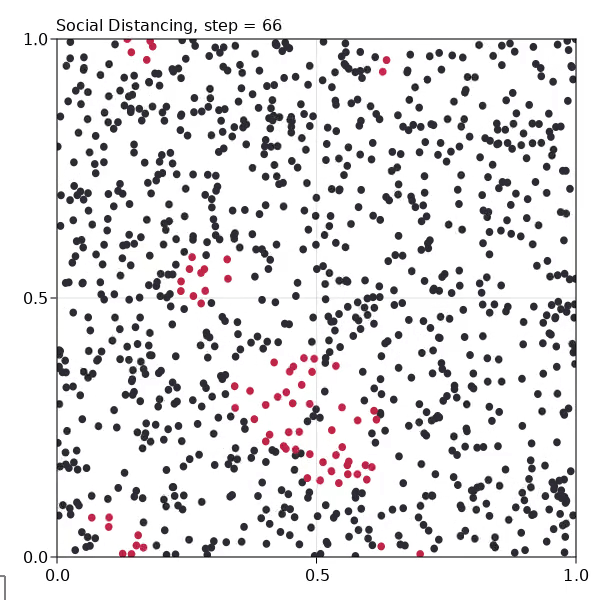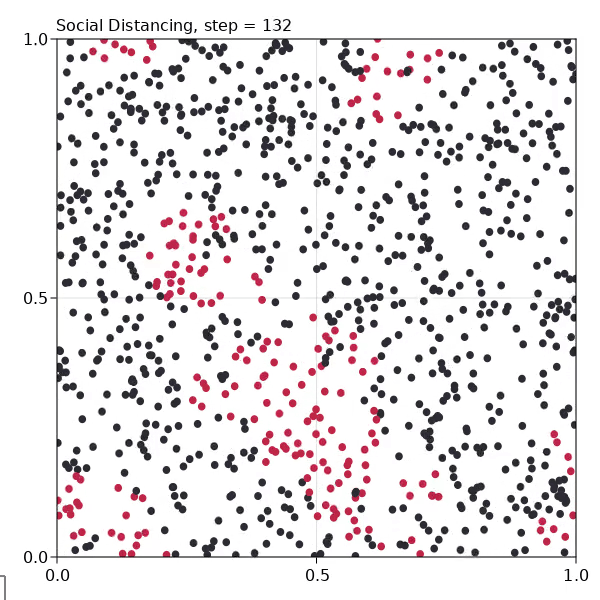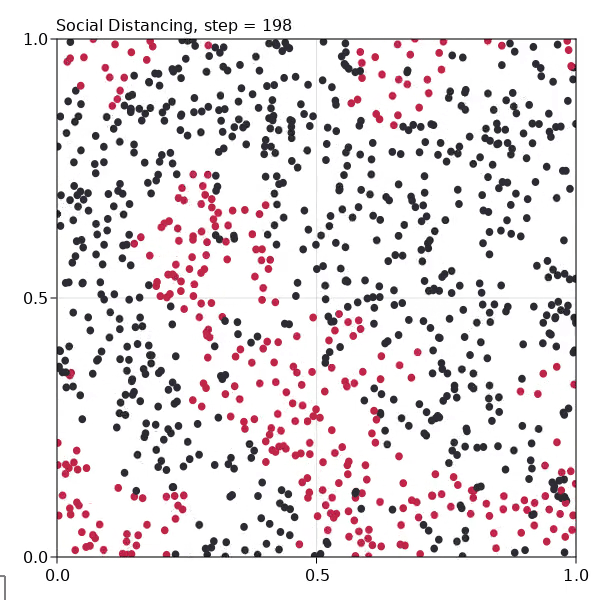
ソーシャルディスタンス
sir_model = sir_initiation(isolated = 0.8)
abm_video(
"socialdist5.gif",
sir_model,
sir_agent_step!,
sir_model_step!;
title = "Social Distancing",
frames = 100,
spf = 2,
ac = sir_colors,
framerate = 20,
)
display("image/gif", read("socialdist5.gif"))

8割動かないagentを作ります。
なかなか刺激的な記述がありました。
Here we let some 20% of the population not be isolated, probably teenagers still partying, or anti-vaxers / flat-earthers that don't believe in science. Still, you can see that the spread of the virus is dramatically contained.
r4 = 0.04
sir_model4 = sir_initiation(reinfection_probability = r4, βmin = β1, isolated = 0.8)
data4, _ = run!(sir_model4, sir_agent_step!, sir_model_step!, 2000; adata)
l4 = lines!(ax, data4[:, dataname((:status, infected))], color = :red)
figure[1, 2] = Legend(
figure,
[l1, l2, l3, l4],
["r=$r1, beta=$β1", "r=$r2, beta=$β1", "r=$r1, beta=$β2", "r=$r4, social distancing"],
)
figure

ソーシャルディスタンスを含めたシミュレーション実行グラフを出力します。ソーシャルディスタンスがある場合、感染拡大が緩やかなカーブになり、感染者数の最大値も低くなっていることが理解できます。
おわりに
感染条件やagentの移動は非常にシンプルなものですが(パラメータは多かったので読み進めるのは大変だったかもしれません)、ミクロなagent同士の相互作用が、SIRモデルに代表されるようなマクロな感染者数の推移に影響を与える様子が分かります。SIRモデルの関連など、なかなか興味深い例題だったと思います。
Discussion