RC4を理解したい(実装編)
諸事情によりこちらへ移行しました。
この記事は2025年4月30日以降に削除する予定です。
はじめに
RC4は、1987年に開発されたストリーム暗号です。ただし、ストリーム暗号としての安全性を満たしておらず、情報の機密性を目的として使用することは非推奨とされています。たとえば、CRYPTREC暗号リストでは、2021年3月31日に運用監視暗号リストからも削除されました。
一方で、マルウェア作成では今でもRC4が使われています。設定ファイルやペイロードを難読化するため、C2通信を難読化するため、ランサムウェアでファイルを暗号化するため、などといった用途があるようです。また、共通鍵暗号の中では構造が比較的シンプルなように見え、まず触ってみる共通鍵暗号にちょうどよさそうです。このような理由から、最近マルウェア解析に入門した立場として、RC4で暗号の独自実装を経験しておくのはよいことだと思いました。
ということで、今回はRC4のアルゴリズムを紹介し、これをC言語で実装してみます。また別の記事で、作成したプログラムをGhidraでリバースエンジニアリングしてみようと思っています。
※注意
・🐺が勉強としてやっているだけなので、参考程度に見てください。
・この記事は予告なく加筆・修正される場合があります
RC4のアルゴリズム
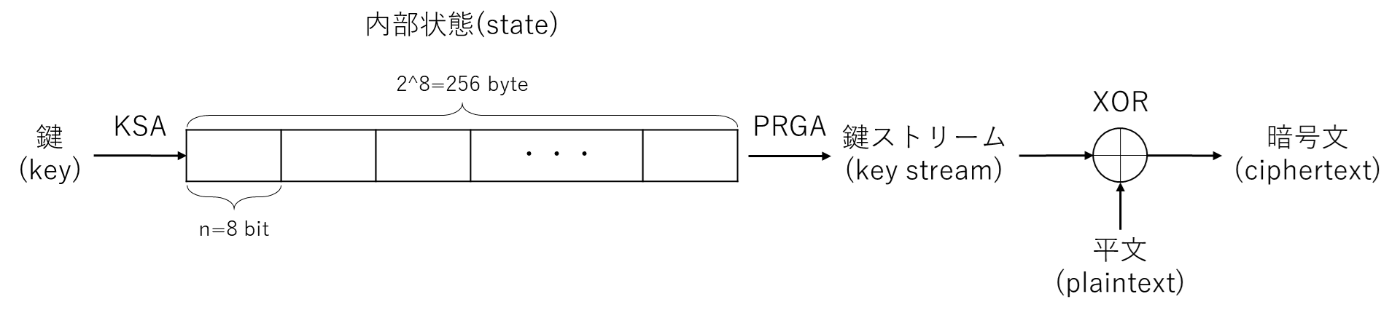
RC4の構造は、2^n byteの値で構成される内部状態(state)と、内部状態の特定の2か所を示す2つのindex (x, y)となります。内部構造の各要素はそれぞれの値はn bitで、n=8が一般的らしいです。ということで、n=8, 2^n=256とします。鍵は1~256 byteの可変長で、16 byte (128 bit)以上が推奨されていたとのことです。
RC4は、2つのアルゴリズム(KSA, PRGA)を経て擬似乱数列を生成し、この擬似乱数列と平文をXORして暗号化します。各ステップでは、それぞれ次のような処理をします。
1. 鍵スケジューリングアルゴリズム(KSA)
鍵を入力として受け取り、内部状態を初期化します。この処理は、入力する鍵の値に依存します。アルゴリズムは次のとおりです。
- i=0からi=2^n-1まで、state[i]=iとする
- j=0とし、i=0からi=2^n-1まで以下を繰り返す
- j←(j+state[i]+key[i mod (key_length)] mod 2^n
- state[i]とstate[j]を入れ替え

これで、内部状態は0~2^nをぐちゃぐちゃに並べ替えた状態になります。
2. 擬似乱数生成アルゴリズム(PRGA)
初期化した内部状態から、擬似乱数列を生成します。アルゴリズムは次のとおりです。
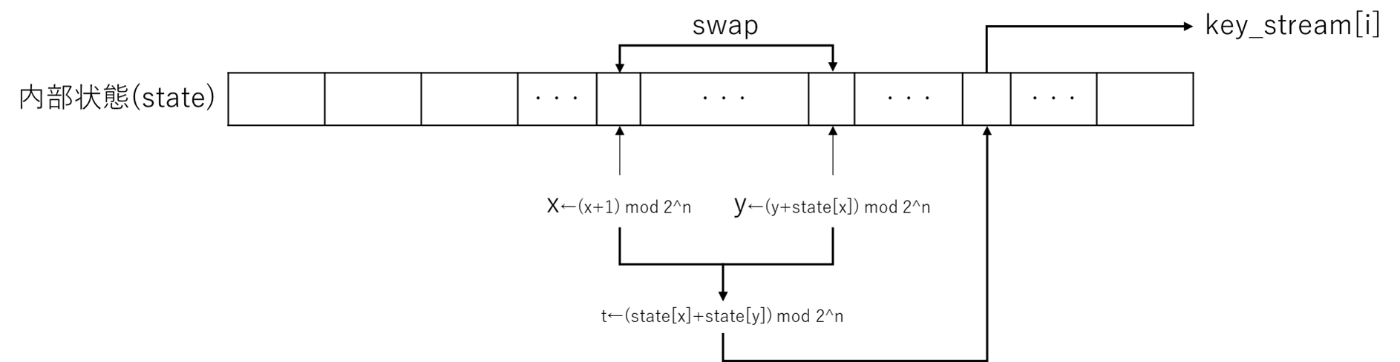
- x=0, y=0とする
- 必要な回数だけ以下を繰り返す
- x←(x+1) mod 2^n
- y←(y+state[x]) mod 2^n
- state[x]とstate[y]を入れ替え
- t←(state[x]+state[y]) mod 2^n
- state[t]を出力
これで、必要な長さの擬似乱数列が得られます。
3. XOR
PRGAの出力として得たkey_streamと平文をXORします。
実装
上記で説明したRC4のアルゴリズムを、C言語で実装してみました。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
# define STATE_LENGTH 0x100
typedef struct {
unsigned char state[STATE_LENGTH];
unsigned char x;
unsigned char y;
} RC4;
void swap(unsigned char* a, unsigned char* b) {
unsigned char tmp = *a;
*a = *b;
*b = tmp;
}
void ksa(RC4* rc4, const char* key, int key_length) {
for (int i = 0; i < STATE_LENGTH; i++) {
rc4->state[i] = i;
}
int j = 0;
for (int i = 0; i < STATE_LENGTH; i++) {
j = (j + rc4->state[i] + key[i % key_length]) % STATE_LENGTH;
swap(&rc4->state[i], &rc4->state[j]);
}
}
void prga(RC4* rc4, unsigned char* key_stream, size_t length) {
rc4->x = 0;
rc4->y = 0;
for (size_t i = 0; i < length; i++) {
rc4->x = (rc4->x + 1) % STATE_LENGTH;
rc4->y = (rc4->y + rc4->state[rc4->x]) % STATE_LENGTH;
swap(&rc4->state[rc4->x], &rc4->state[rc4->y]);
int t = (rc4->state[rc4->x] + rc4->state[rc4->y]) % STATE_LENGTH;
key_stream[i] = rc4->state[t];
}
}
void xor_encrypt(const char* plaintext, size_t text_length, unsigned char* key_stream, unsigned char* ciphertext) {
for (size_t i = 0; i < text_length; i++) {
ciphertext[i] = plaintext[i] ^ key_stream[i];
}
}
unsigned char* rc4(const char* key, const char* plaintext) {
RC4 rc4;
size_t text_length = strlen(plaintext);
unsigned char* key_stream = (unsigned char*)malloc(text_length * sizeof(unsigned char));
unsigned char* ciphertext = (unsigned char*)malloc(strlen(plaintext) * sizeof(unsigned char));
ksa(&rc4, key, strlen(key));
prga(&rc4, key_stream, text_length);
xor_encrypt(plaintext, text_length, key_stream, ciphertext);
free(key_stream);
return ciphertext;
}
int main(void) {
const char key[] = "this_is_my_key"; // 使用する鍵
const char* plaintext = "plaintext"; // 暗号化する文字列
unsigned char* ciphertext = rc4(key, plaintext);
printf("ciphertext: ");
for (size_t i = 0; i < strlen(plaintext); ++i) {
printf("%02X", ciphertext[i]);
}
printf("\n");
free(ciphertext);
return 0;
}
出力は次のとおりでした。
ciphertext: F1E19E3D882F3F091E
ちゃんと動いているか、CyberChefで復号して確認しておきます。
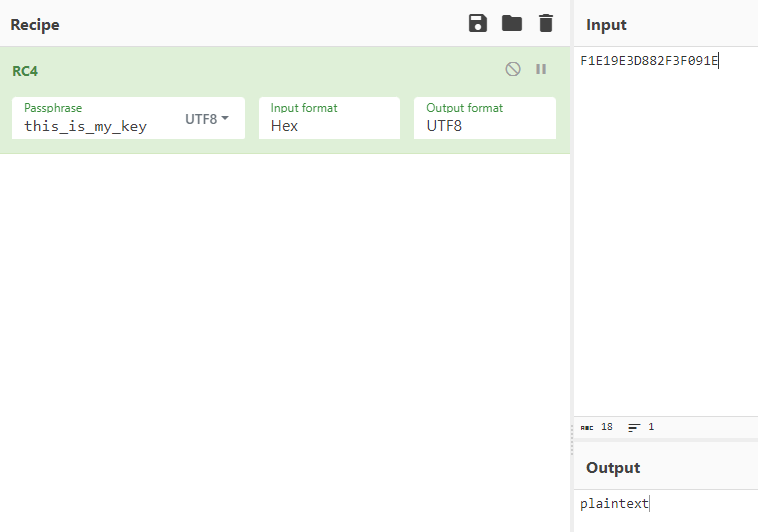
大丈夫そうですね。
おわりに
ストリーム暗号RC4のアルゴリズムを紹介し、C言語で実装しました。C言語を書くのが久しぶりでいろいろと苦労はしましたが、ちゃんと動くものをなんとか作れたはずです。共通鍵暗号を実装したことはなかったので、とてもよい経験になったと思います。
Discussion