緑コーダーの参加記録: ABC186 D - Sum of difference

問題

https://atcoder.jp/contests/abc186/tasks/abc186_d

解法

開く

1. $A$ を降順にソートする
2. $\sum_{i = 1}^{N} (N - 2i + 1) A_i$ を出力する

解説

そのまま計算しようとすると $O(N^2)$ になりますが、制約は $N \le 2\times10^5$ なのでそのままだとTLEしてしまいます。
そこで、計算量を落とすことを考えます。

$1 \le i \lt j \le N$ を満たす全ての $(i, j)$ の組は $\binom{N}{2}$ 個あり、２つの異なる要素に対しての差を計算することが求められているとわかります。
２つの異なる要素であればよいので、 $A$ を並び替えても答えは変化しません。降順にソートすることで $A_i \ge A_j$ となり、絶対値を外すことができます。

$$\sum_{i = 1}^{N-1} \sum_{j = i+1}^{N} (A_i - A_j)$$

計算を簡単にするために、この式を２つに分割します。

$$\sum_{i = 1}^{N-1} \sum_{j = i+1}^{N} A_i - \sum_{i = 1}^{N-1} \sum_{j = i+1}^{N} A_j$$

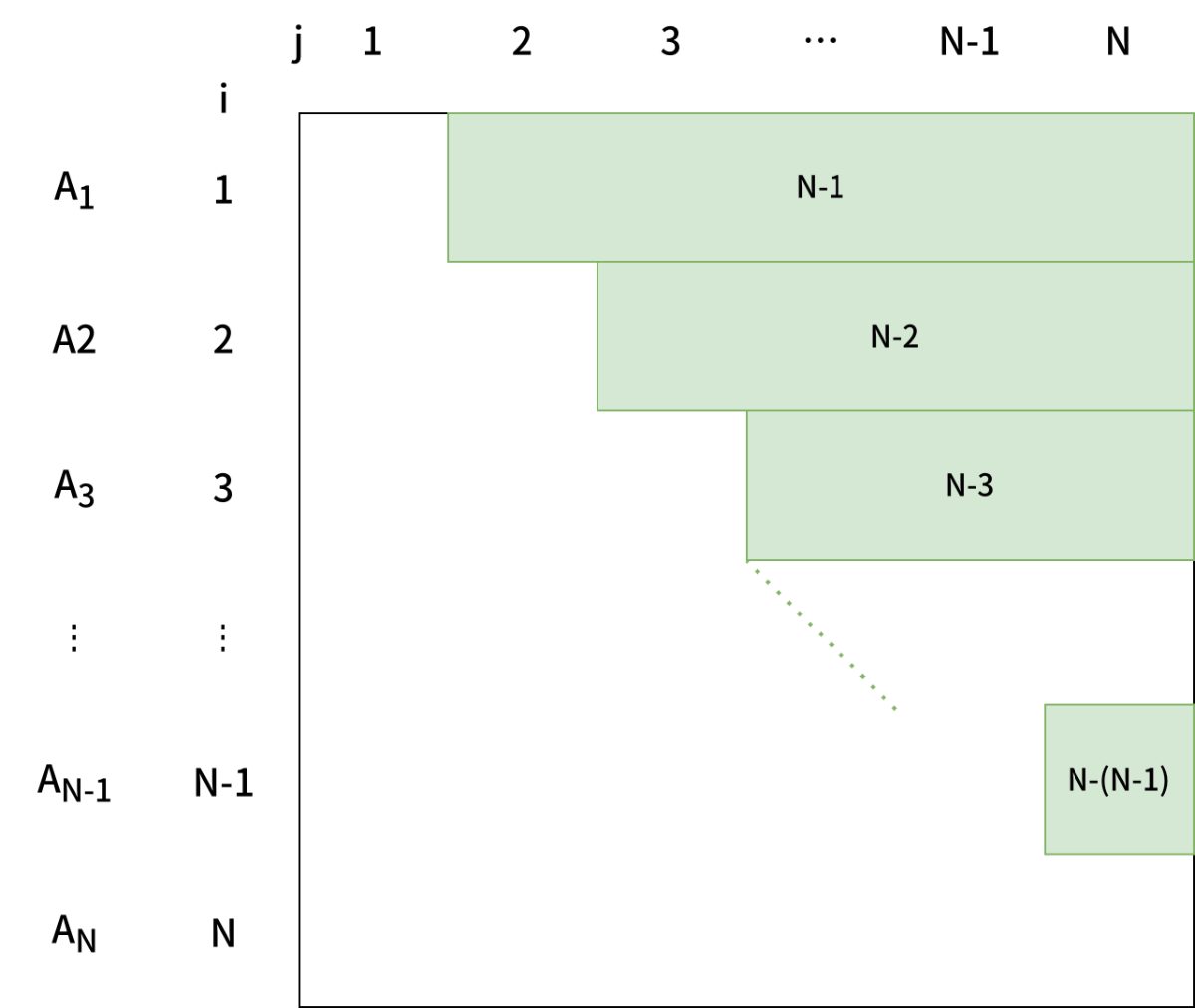
$A_i$ の和や、 $A_j$ の和はどのような形になっているでしょうか。図を描いてみます。

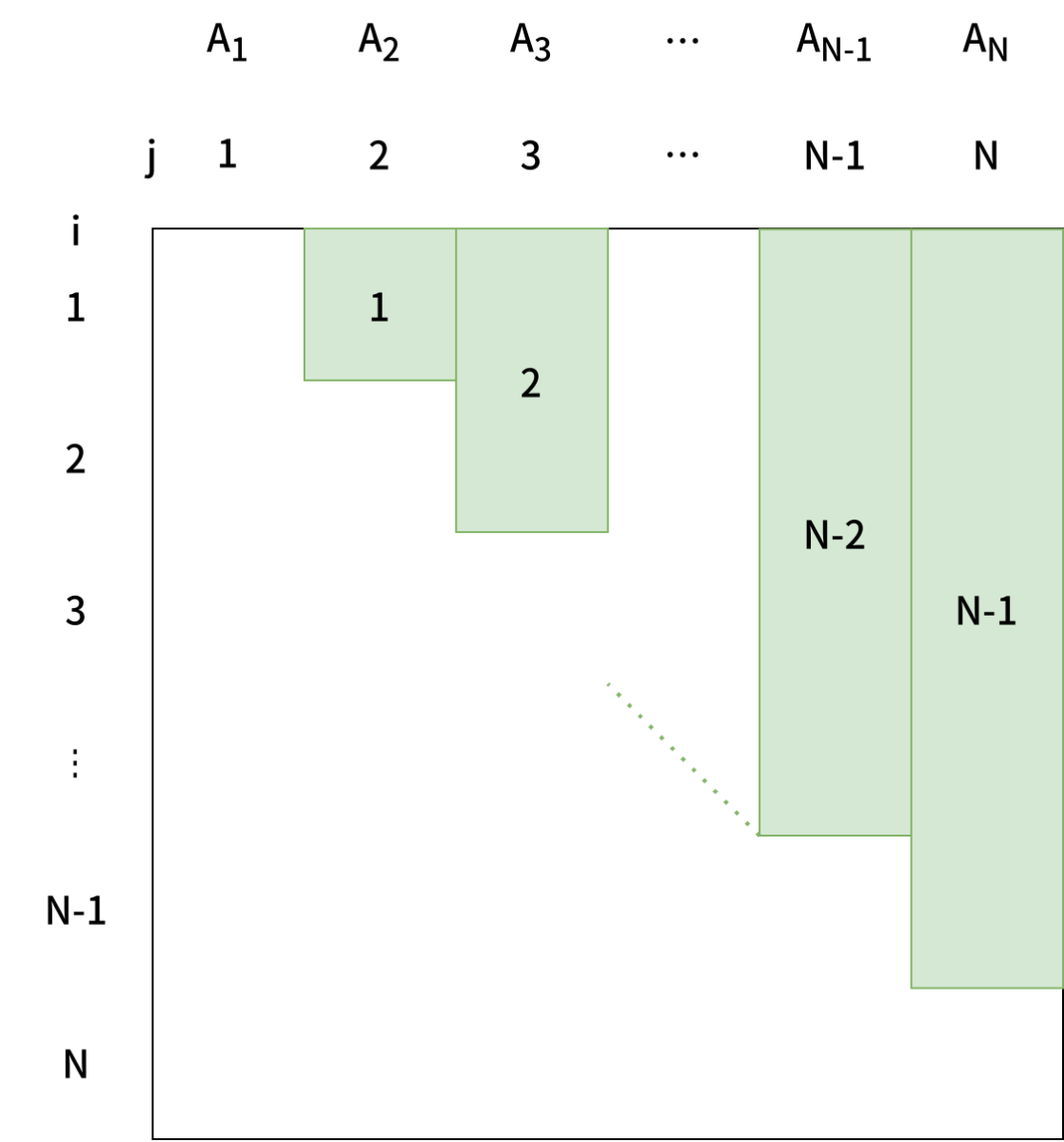
$\sum_{i = 1}^{N-1} \sum_{j = i+1}^{N} A_i$	$\sum_{i = 1}^{N-1} \sum_{j = i+1}^{N} A_j$
$$\sum_{i = 1}^{N} (N-i) A_i$$	$$\sum_{j = 1}^{N} (j-1) A_j$$

これで、 $O(N)$ で計算することができます。
ついでに式をまとめてシンプルにしてしまいます。

$$\sum_{i = 1}^{N} (N-i) A_i - \sum_{j = 1}^{N} (j-1) A_j \\ = \sum_{i = 1}^{N} (N-i) A_i - \sum_{i = 1}^{N} (i-1) A_i \\ = \sum_{i = 1}^{N} (N - 2i + 1) A_i$$

ポイント

• 絶対値を外す方法を考える
• 総和の式を2次元的に考える

コード

abc186_d.rb

N = gets.to_i
A = gets.split.map(&:to_i).sort.reverse!
puts (1..N).sum { |i| (N - i * 2 + 1) * A[i-1] }