2-SATを解く
この記事は「木 Advent Calendar 2023」の18日目です。
きのうの記事はうえきさんの「木のおもしろあるあるを書きました!」でした。
あしたの記事はまぐふらいさんの「LowLinkの紹介」です。
今日は真面目な記事なので真面目に書きます。
2-SAT とは
まずは SAT (充足可能性問題) について
説明は Wikipedia に譲ります(上のリンクをクリック!)
2-SAT (CNF-SAT のうち、節内のリテラルが高々
本記事ではこの 2-SAT について、与えられた論理式の充足可能性を判定する方法と、充足する割当を計算する方法を紹介します。
ちなみに、 2-SAT の割当の数え上げは ♯P-complete であり、効率的に解く方法は存在しないと考えられています。
2-SAT を解く
2-SAT における充足可能性の判定は、論理式を有向グラフに変換することにより行います。
この有向グラフは 含意グラフ (implication graph) と呼ばれ、論理式における
論理式を含意グラフに変換する
論理式を含意グラフに変換するには、以下の通りの手順をたどります。
- まず、それぞれの変数と、それぞれの変数の否定に対応する
2N - たとえば、変数が
x, y, z \bar{x}, \bar{y}, \bar{z}
- たとえば、変数が
- それぞれの節
(A \vee B) \bar{A} \to B \bar{B} \to A - たとえば、
(x \vee y) \bar{x} \to y \bar{y} \to x -
(x \vee \bar{y}) \bar{x} \to \bar{y} y \to x - もし節が
(A \to B) A \to B \bar{B} \to \bar{A}
- たとえば、
これで含意グラフができました。
含意グラフ上で
練習問題
論理式を含意グラフに変換してみましょう。
例題
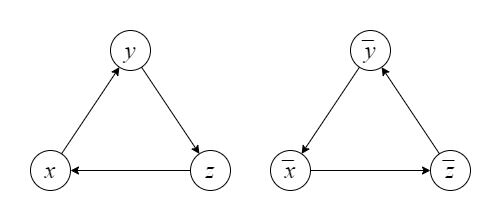
問題
解答

充足可能な割当て
含意グラフ上で
(仮にそのようなパスがなければ、
すると、以下の3通りが考えられます。
- (a)
x \to \bar x - この場合、
x = 1 \bar x = 0 x = 0
- この場合、
- (b)
\bar x \to x - この場合、
\bar x = 1 x = 0 x = 1
- この場合、
- (c)
x \to \bar x \bar x \to x x \bar x - この場合、充足可能な割当は存在しません。
このように各変数について割当を行うことで、解を求めることができます。
- この場合、充足可能な割当は存在しません。
強連結成分分解を使う
上に示したことは、含意グラフを強連結成分分解・トポロジカルソートすることで求めることができます。
(c) についてはそのまま判定すればよいです。
ただし (a), (b) については、 DAG 上で 2 点間を結ぶパスが存在するかの判定を行うと時間がかかるため、単にトポロジカル順で判定します。
- まず、同じ強連結成分内に
x \bar x x - トポロジカル順で後に来る頂点から順に割当を決めていきます。基本的に
1 0
含意グラフの頂点は
それで、これがどう木と関係あるのでしょう?
ノーコメントとさせていただきます。
Discussion