✨

ABC239 G 解説

2022/02/20に公開

競技プログラミング

「頂点 $1$ から頂点 $N$ へ行くパスを消すための最小コストを求めろ」という典型的な最小カット問題です。

コストを求める

まずは、与えられるグラフを描いてみます。サンプル 1 のグラフがこちらになります。

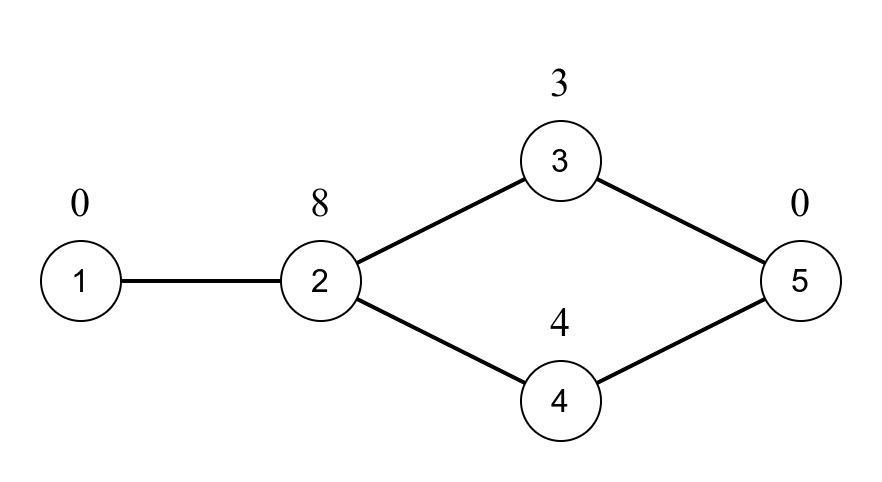
サンプル1 そのまま描いたグラフ

最小カットは辺のコストですが、この場合は頂点にコストがついています。ここで、フロー問題の典型テクニックの一つ、「頂点を辺にする」を使います。
具体的に言うと、頂点を「入頂点」と「出頂点」のふたつに分割して、出頂点から入頂点に頂点のコストがついた辺を貼ります。

そうしてできたグラフがこちらになります。

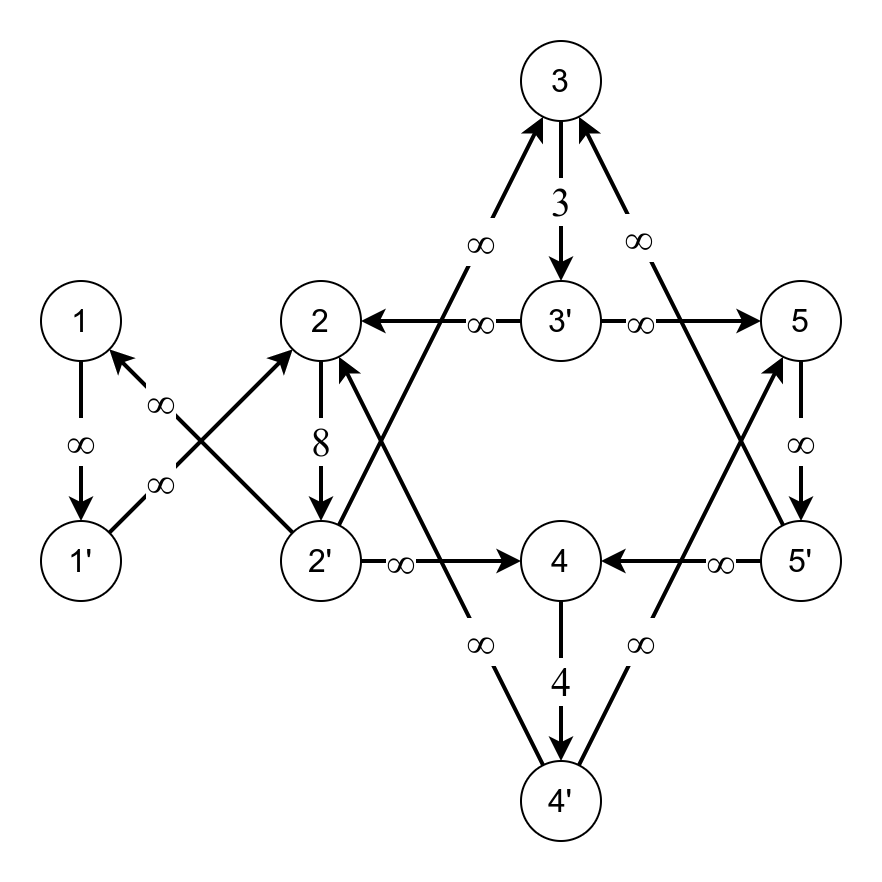
サンプル1 頂点を分割したグラフ

頂点 $i$ から $i'$ への辺には、コスト $c_i$ があります。
なお、頂点 $1$ と頂点 $N$ は壁を建てられないので、コストは $\infty$ としています。

そして、このグラフで $1$ から $N'$ へフローを流すことでコストを求めることができます。
フローを流すと、このようになります。フローが流れている辺のうち、容量いっぱいにフローが流れているものが、カットとなりうる辺です。

サンプル1 フローを流した

カットを求める

このようにして、最小カットを求めることができました。しかし、この問題ではそれだけではなく、カットとなる辺も求める必要があります。

カットとなる辺は、残余グラフ^[1]上で頂点 $1$ からの DFS をすることによって求まります。頂点 $1$ から到達できる頂点から到達できない頂点への辺がカットとなる辺です。

以下は、サンプル 1 のグラフにおいて、頂点 $1$ から到達できる頂点を赤く塗ったグラフです。

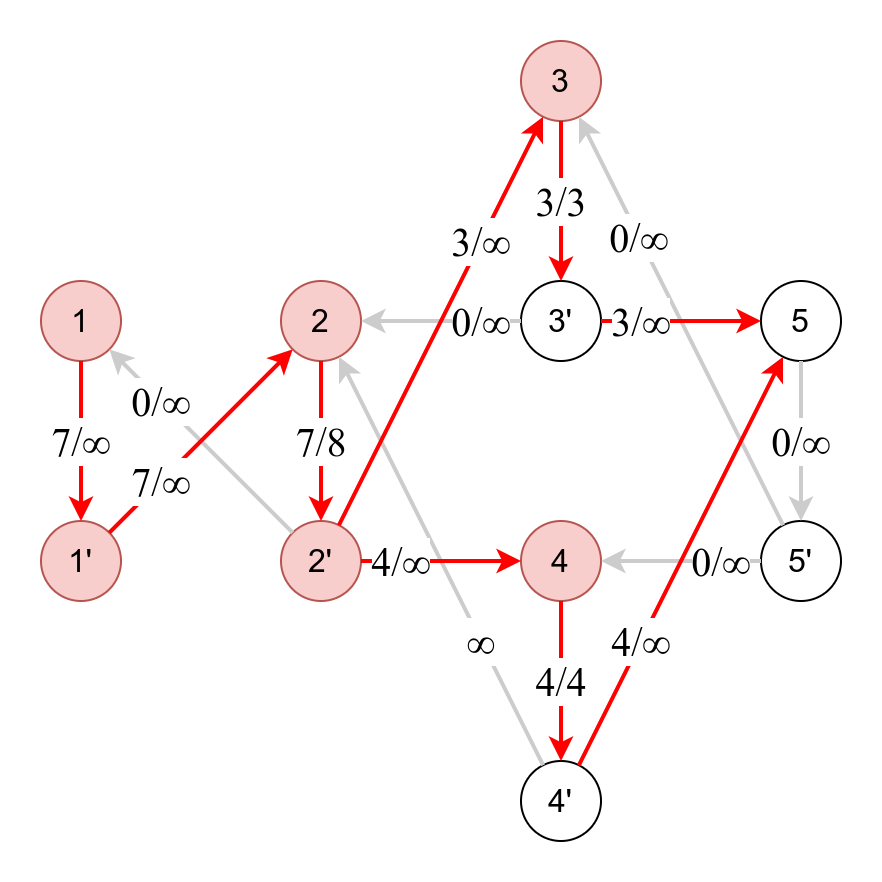
サンプル1 カット

このグラフにおいては、カットが辺 $3\to3'$ と $4\to4'$ であることがわかります。

ACL の maxflow においては、 min_cut によって到達可能性の判定ができます。

提出コード

#include <bits/stdc++.h>
using namespace std;
#include <atcoder/maxflow>
using namespace atcoder;

using ll = long long;
const ll INF = 1001001001001001001LL;

#define rep(i, l, r) for (auto i = (l); i != (r); i++)

int main() {
  int N, M;
  cin >> N >> M;
  // 入頂点を N+i 、出頂点を i としている
  mf_graph<ll> g(N * 2);
  
  rep (i, 0, M) {
    int a, b;
    cin >> a >> b;
    a--, b--;
    g.add_edge(N + a, b, INF);
    g.add_edge(N + b, a, INF);
  }
  
  vector<ll> c(N);
  rep (i, 0, N) cin >> c[i];
  c[0] = c[N - 1] = INF;
  
  rep (i, 0, N)
    g.add_edge(i, N + i, c[i]);
  
  ll mincut = g.flow(N, N - 1); // 提出コード上では 0 から N + (N - 1) となっていますが、（一応それでも合いますが）頂点 1 の入頂点から頂点 N の出頂点へと考えるとこちらの方が正しいです
  auto reachable = g.min_cut(0);
  
  vector<int> ans;
  rep (i, 0, N)
    if (reachable[i] && !reachable[N + i])
      ans.push_back(i + 1);
  
  cout << mincut << endl;
  cout << ans.size() << endl;
  rep (i, 0, ans.size())
    cout << ans[i] << " \n"[i == ans.size() - 1];
}

脚注

元のグラフのすべての辺について、容量が（容量-フロー）となる辺を追加したもの。 ACL を利用されている方は知らなくても問題ないですし、ご自分でフローを計算されている方はもともとご存知のはずなので、必要ない注釈かもしれません。 ↩︎

コストを求める

カットを求める

提出コード

Discussion