RustでSkipListを作った話
Skip Listとは
乱択アルゴリズム用いた,ノードが複数レベルの遷移を持つソートされた連結リストです.
1989年にウィリアム・ピューという方が発表したデータ構造らしいです.[1]
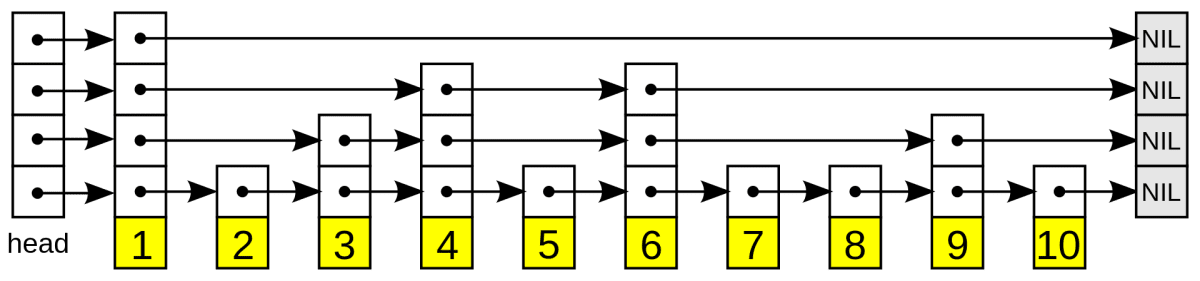
SkipListの例 (Wikipediaより引用)
上の図のようにSkip Listはノードが複数レベルの遷移を持っています.
上位の遷移でノードを飛び越すことによって高速に操作することが出来ます.
Skip Listの性能は遷移の構成の仕方に依存することが見て取れると思います.例えば,全てのノードが同じレベルであった場合を考えると,単なる連結リストと同じ性能になってしまいますね.
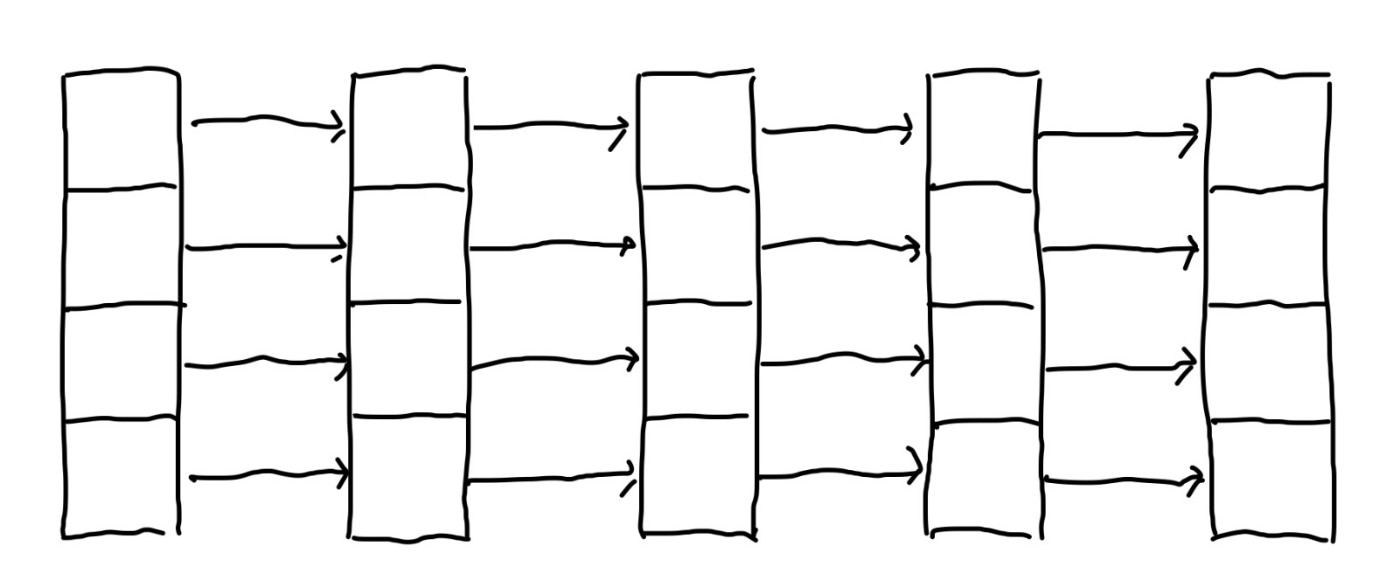
Skip Listの最悪ケース
最もよい繋ぎ方を考えてみましょう.二分木から連想すれば,一回の遷移で半分の要素を飛び越せればよさそうです.
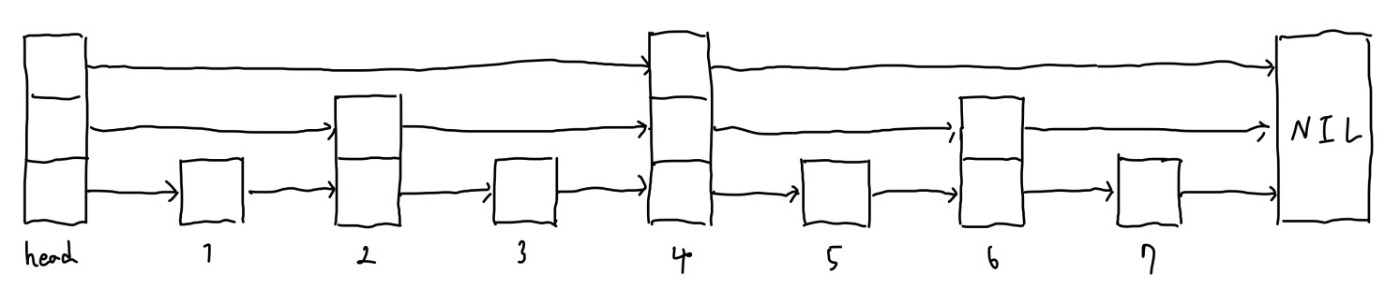
Skip Listの最良ケース
上の図の様な繋ぎ方が最良の繋ぎ方になります.これを見ると確率的である必要は感じないかもしれません.
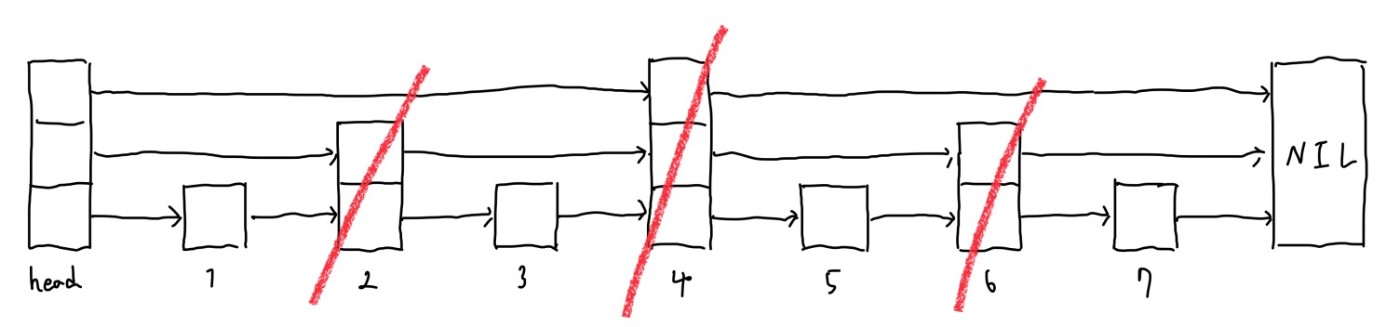
ここで,高いレベルのノードを削除してみます.
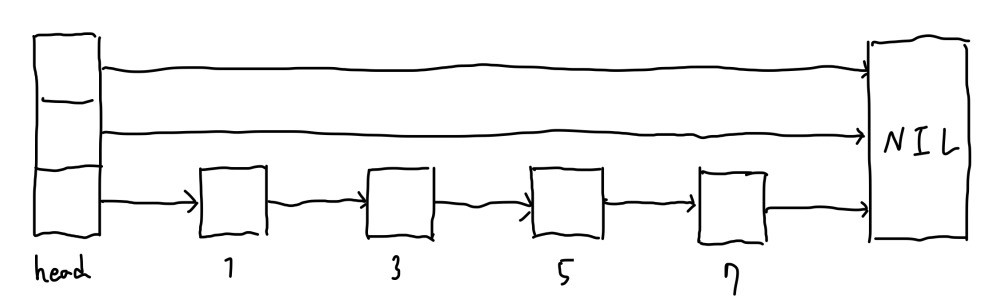
連結リストと同じ構造になってしまいました.これでは性能が劣化してしまいますね.
この様に,決定的にノードの高さを選ぶと故意に性能を劣化させることが出来てしまいます.
こういった攻撃に耐性を持つために確率的にノードの高さを選択する必要があったわけです.
具体的に高さは,パラメータ
余談
単に確率で高さを選ぶと上限なくノードが高くなってしまいます.不必要にノードを高くしないために,要素数に応じた高さの上限を設けます.例えば
次の章ではRustでこれを実装します.
参考にした論文は以下です.
Skip Lists: A Probabilistic Alternative to Balanced Trees
実装
Skip Listの構造上,同じノードを複数のノードが所有します.これはRustの所有権と相性が悪く,ポインタを多用した実装になります.
また,ノードを可変長にしましたがRustは可変長構造体を直接インスタンス化する方法がなく,fat pointerを作成する機能がnightlyであるためu8のポインタをそのまま使います.
Node
// key: K + value: V + level: usize + nexts: [MaybeNode<K, V>]
pub struct Node<K: Ord, V> {
ptr: NonNull<u8>,
marker: PhantomData<(K, V)>,
}
pub struct MaybeNode<K: Ord, V> {
ptr: *mut u8,
marker: PhantomData<(K, V)>,
}
nullを表す必要があるので,MaybeNodeとNodeで型を分けます.
複数のNodeが同じポインタを所有することがあります.
MaybeNodeにはtakeというメソッドがあり,Option<Node>を返します.
Nodeにはkey, value, level, nextsというメソッドがあり,無制限のライフタイムを持つ参照を返します.
list
pub struct SkipList<K: Ord, V, G: Generator<bool>> {
gen: G,
count: usize,
nodes: Vec<MaybeNode<K, V>>,
}
nodesが各レベルの先頭要素への参照になり,常に最大レベル以上の長さを持ちます.
search
探索アルゴリズムはシンプルで,keyを探す場合,
- 最も高いレベルから探索を始める
- そのレベルにおいて見つけたい要素未満で最も大きい要素を見つける.
- レベルが0なら5.へ移動.
- レベルを1下げ,2.へ移動.
- 次の要素が,keyであればその要素を返す.そうでなければ失敗.
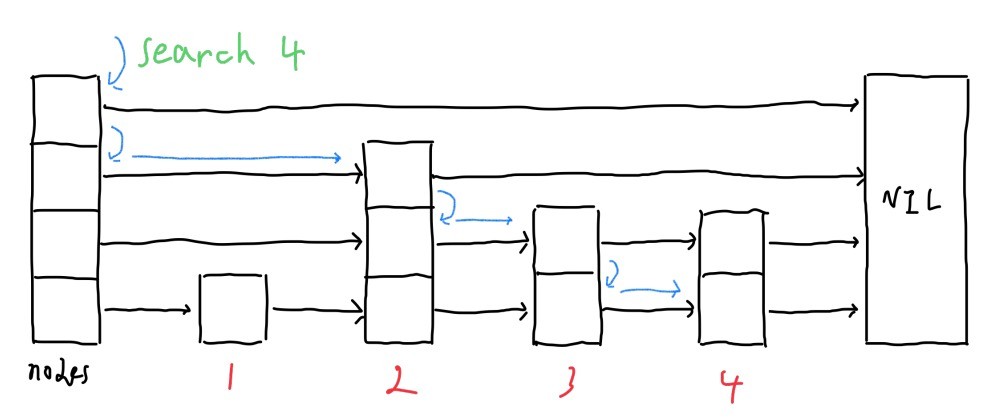
pub fn search(&self, key: &K) -> Option<&V> {
// SkipListかNodeの遷移テーブル
let mut forwards = self.nodes.as_slice();
// 最も高いレベルから0までループ
for level in (0..forwards.len()).rev() {
// 次の要素がnullか,探しているkey以上になるまで前方に進める.
// -> forwardsはnullの手前か,key未満で最大の要素の手前の要素のテーブルになる.
loop {
let Some(next) = forwards.get(level).and_then(|e| e.take()) else {
break;
};
if next.key() >= key {
break;
}
forwards = next.nexts();
}
}
// 次の要素がnullなら失敗
let Some(node) = forwards.get(0).and_then(|e| e.take()) else {
return None;
};
if node.key() == key {
Some(node.value())
} else {
None
}
}
insert
insertもsearchと同様にレベルごとに前に進めていく形になります.
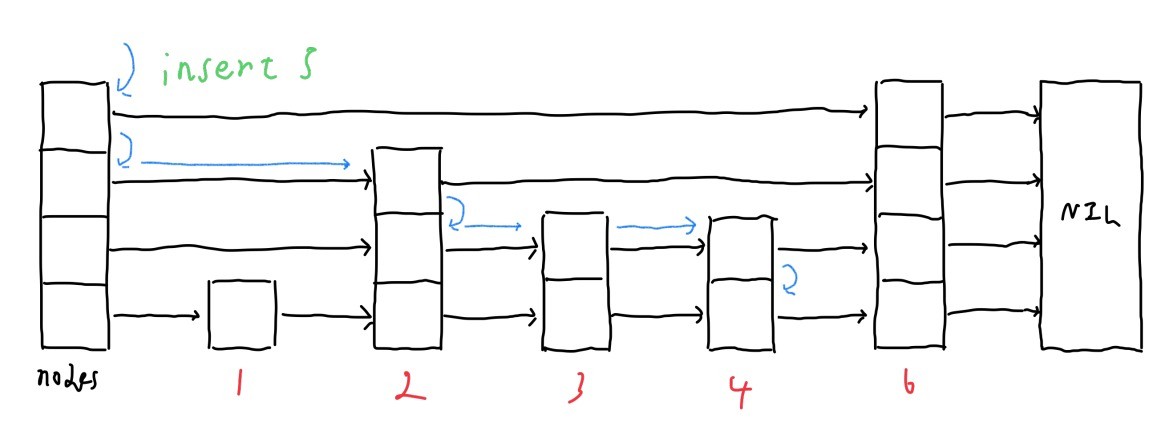
ですが,insertと異なりノードを繋ぎ直す必要があるため,経路を記憶する必要があります.
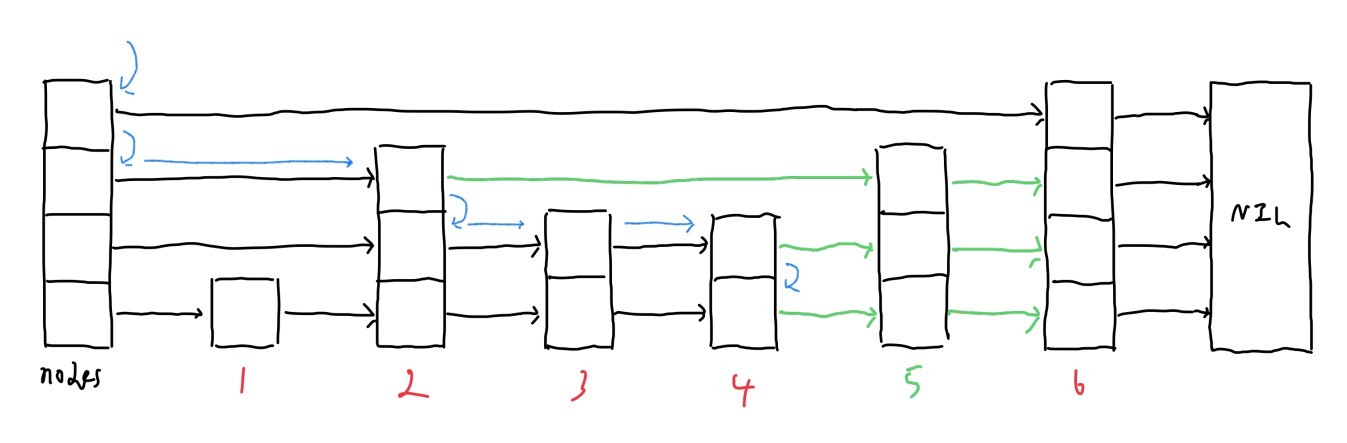
そのため,レベルごとに再帰を行って,そのレベルでの一番前の遷移テーブルを記憶します.
pub fn insert(&mut self, key: K, value: V) -> Result<(), (K, V)> {
let len = self.nodes.len();
let level = len - 1;
let forwards = unsafe { std::slice::from_raw_parts_mut(self.nodes.as_mut_ptr(), len) };
let inserted = self.insert_impl(forwards, level, key, value)?;
// 挿入されたノードのレベルが今までの最大レベルより高い場合,先頭を拡大する必要がある.
if let Some(d) = inserted.level().checked_sub(len) {
self.nodes
.extend(repeat::<MaybeNode<K, V>>(inserted.into()).take(d));
}
Ok(())
}
// 各レベル毎でforwardsを保存しておく必要があるため,
// searchでのlevelに関するforループに当たるものを再帰で行う.
fn insert_impl(
&mut self,
mut forwards: &mut [MaybeNode<K, V>],
level: usize,
key: K,
value: V,
) -> Result<Node<K, V>, (K, V)> {
loop {
//前方に進める.
assert!(level < forwards.len());
let Some(next) = forwards[level].take() else {
break;
};
if next.key() == &key {
return Err((key, value));
}
if next.key() > &key {
break;
}
forwards = next.nexts_mut();
}
let node = if level == 0 {
let n = self.alloc(key, value);
self.count += 1;
n
} else {
self.insert_impl(forwards, level - 1, key, value)?
};
if level >= node.level() {
return Ok(node);
}
node.nexts_mut()[level] = forwards[level];
forwards[level] = node.into();
return Ok(node);
}
論文ではinsertに再帰を用いず,最大レベルの長さを持つ配列を使って,変更すべき遷移を記憶していました.
しかし,Rustには可変長配列のスタック確保の方法はなく,再帰深度の上限も対数スケールであるため,再帰で実装しました.
removeはinsertとほぼ同じコードで実装できます.
まとめ
二分木と比べるとアルゴリズムはシンプルであると思いますが,Rustとは相性が悪く,可変長型と所有権によって実装が複雑になってしまいました.
プログラム全体は以下のリポジトリに公開しています.
追記
- 2023/09/07:
- ライフタイム制限を避けるためポインタを経由していた部分をunbound lifetimeを利用する形にしました.
- insertの図において経路に誤りがあったため修正しました.
Discussion