個人的に忘れがちなシェーダー関数メモ [SKShader/MSL/GLSL]
こまかい仕様を忘れがちなシェーダーの関数の雑メモです。
ひさしぶりにシェーダーを書いたときによく調べなおしている関数を記録しておく場所として。
いいかんじの図を集めて体裁を整えられたら記事に移行するかもしれません。
主な動作確認環境
- SKShader iOS 15.2 / macOS 12.1 (Swift Playgrounds 4.5.3で確認)
- Metal Shading Language 3.2 (同上、SceneKitのSCNShadableで確認)
- GLSL ES 1.0 / 3.0 (GLSL Editor / Shadertoy)
※2025/4/1 時点。雑メモなので厳密な確認をしていないことがあります。
主なドキュメント
丸め系
| x | floor(x) | ceil(x) | trunc(x) *SK *M *GL3 |
round(x) *SK *M *GL3 |
roundEven(x) *GL3 |
rint(x) *SK *M |
|---|---|---|---|---|---|---|
| 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| 1.75 | 1.0 | 2.0 | 1.0 | 2.0 | 2.0 | 2.0 |
| 1.5 | 1.0 | 2.0 | 1.0 | 2.0 | 2.0 | 2.0 |
| 1.25 | 1.0 | 2.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.75 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| 0.5 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 0.25 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| -0.25 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| -0.5 | -1.0 | 0.0 | 0.0 | -1.0 | 0.0 | 0.0 |
| -0.75 | -1.0 | 0.0 | 0.0 | -1.0 | -1.0 | -1.0 |
| -1.0 | -1.0 | -1.0 | -1.0 | -1.0 | -1.0 | -1.0 |
| -1.25 | -2.0 | -1.0 | -1.0 | -1.0 | -1.0 | -1.0 |
| -1.5 | -2.0 | -1.0 | -1.0 | -2.0 | -2.0 | -2.0 |
| -1.75 | -2.0 | -1.0 | -1.0 | -2.0 | -2.0 | -2.0 |
| -2.0 | -2.0 | -2.0 | -2.0 | -2.0 | -2.0 | -2.0 |
*SK = SKShaderの関数
*M = MSLの関数
*GL3 = GLSL ES 3.0の関数
メモ
丸め系の関数は負値を渡したときの戻り値を忘れがち。
floor は小さいほうの整数へ切り捨てる
-1.25 は -1.0 ではなく -2.0 になる
Swiftの FloatingPointRoundingRule.down の挙動
ceil は大きいほうの整数へ切り上げる
-1.25 は -2.0 ではなく -1.0 になる
Swiftの FloatingPointRoundingRule.up の挙動
trunc はゼロに近いほうの整数へ丸める
-1.25 は -2.0 ではなく -1.0 になる
正値では floor と同じ結果、負値では ceil と同じ結果になる
小数部分が .0 になると覚えればよい
Swiftの FloatingPointRoundingRule.towardZero の挙動
GLSL ES 1.0でtruncしたいときは x - fract(abs(x)) * sign(x) や、xがfloatなら x < 0.0 ? ceil(x) : floor(x) など
round は四捨五入する
-0.5 は -1.0 、 0.5 は 1.0 になる (※GLSLでは環境依存)
Swiftの FloatingPointRoundingRule.toNearestOrAwayFromZero の挙動
GLSL ES 3.0の roundEven とMSLの rint は四捨五入する
偶数と奇数の境目にある数値(..., -1.5, -0.5, 0.5, 1.5, ...)が偶数側へ丸められる点が round と異なる
-0.5 は 0.0 、 -1.5 は -2.0 、 -2.5 は -2.0 になる
Swiftの FloatingPointRoundingRule.toNearestOrEven の挙動
Swiftの FloatingPointRoundingRule.awayFromZero の挙動をする関数は無し
x + fract(-abs(x)) * sign(x) や、xがfloatなら x < 0.0 ? floor(x) : ceil(x) など
小数部系
| x | fract(x) | mod(x, 1.0) *SK *GL |
fmod(x, 1.0) *SK *M |
|---|---|---|---|
| 2.0 | 0.0 | 0.0 | 0.0 |
| 1.75 | 0.75 | 0.75 | 0.75 |
| 1.5 | 0.5 | 0.5 | 0.5 |
| 1.25 | 0.25 | 0.25 | 0.25 |
| 1.0 | 0.0 | 0.0 | 0.0 |
| 0.75 | 0.75 | 0.75 | 0.75 |
| 0.5 | 0.5 | 0.5 | 0.5 |
| 0.25 | 0.25 | 0.25 | 0.25 |
| 0.0 | 0.0 | 0.0 | 0.0 |
| -0.25 | 0.75 | 0.75 | -0.25 |
| -0.5 | 0.5 | 0.5 | -0.5 |
| -0.75 | 0.25 | 0.25 | -0.75 |
| -1.0 | 0.0 | 0.0 | 0.0 |
| -1.25 | 0.75 | 0.75 | -0.25 |
| -1.5 | 0.5 | 0.5 | -0.5 |
| -1.75 | 0.25 | 0.25 | -0.75 |
| -2.0 | 0.0 | 0.0 | 0.0 |
*SK = SKShaderの関数
*M = MSLの関数
*GL = GLSL ES 1.0/3.0の関数
メモ
小数部系の関数も負値を渡したときの戻り値を忘れがち。
fract と mod(x, 1.0) の結果は同じ
-1.25 は -0.25 ではなく 0.75 になる
fmod(x, 1.0) は負値側の戻り値が mod(x, 1.0) と異なる
-1.25 は 0.75 ではなく -0.25 になる
mod(x, y) の計算式は x - y * floor(x / y)
fmod(x, y) の計算式は x - y * trunc(x / y)
二値化
| x | step(0.0, x) | step(x, 0.0) |
|---|---|---|
| 1.0 | 1.0 | 0.0 |
| 0.5 | 1.0 | 0.0 |
| 0.0 | 1.0 | 1.0 |
| -0.5 | 0.0 | 1.0 |
| -1.0 | 0.0 | 1.0 |
メモ
引数は step(edge, x) の順で、戻り値は x < edge ? 0.0 : 1.0
この公式ドキュメントに書かれている引数の順序と大小の向きが直感と合わなくて書きかたを迷いがち
args1 <= args2 ? 1.0 : 0.0 なので第二引数の方が大きければ1.0、同値の場合も1.0になる
変換行列
拡大縮小 (Scale)
mat2 scale(vec2 _scale) {
return mat2(
_scale.x, 0.0,
0.0, _scale.y
);
}
scale(vec2(1.5, 0.5)) * coordinates.xy で、座標がX方向に1.5倍、Y方向に0.5倍になる。
| 変形前 | 変形後 |
|---|---|
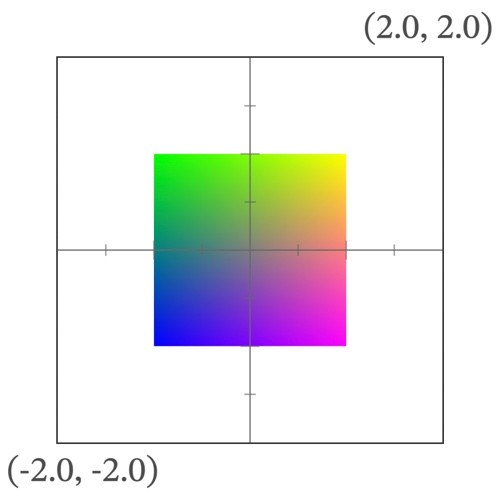 |
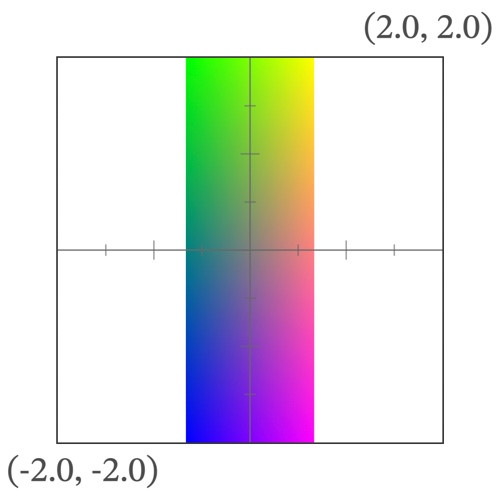 |
次のような関数にすると、座標ではなくシェーダーで描画している図形の拡大・縮小になる。
こちらのほうが感覚的に使いやすい場合もある。
mat2 scale(vec2 _scale) {
return mat2(
1.0 / _scale.x, 0.0,
0.0, 1.0 / _scale.y
);
}
scale(vec2(1.5, 0.5)) * coordinates.xy で、描画している図形がX方向に1.5倍、Y方向に0.5倍になる。
| 変形前 | 変形後 |
|---|---|
 |
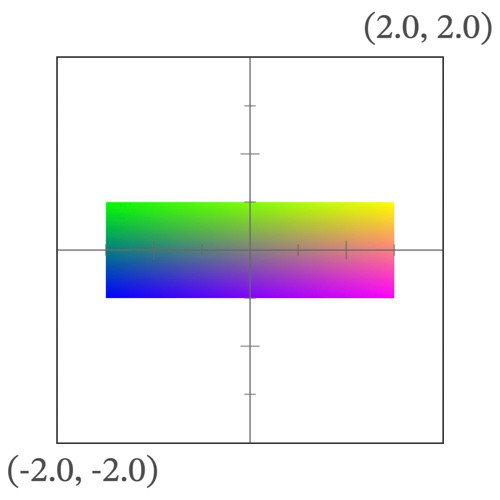 |
回転 (Rotate)
mat2 rotate(float _angle) {
return mat2(
cos(_angle), -sin(_angle),
sin(_angle), cos(_angle)
);
}
rotate(45.0 / 180.0 * 3.1415927) * coordinates.xy で、原点を中心として反時計回りに45度回転する(右手系の座標の場合)。
| 変形前 | 変形後 |
|---|---|
 |
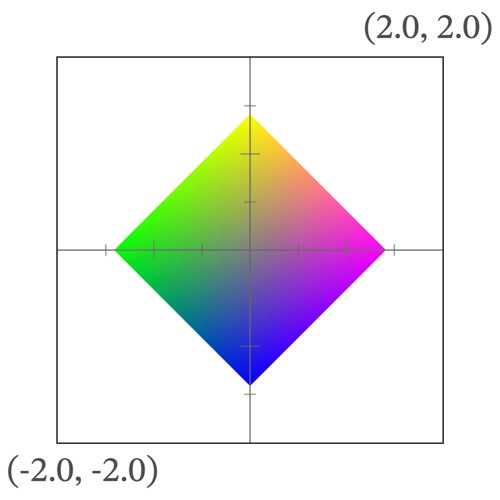 |
剪断 (せん断 / Shear / Skew)
mat2 shear(vec2 _shear) {
return mat2(
1.0, _shear.y,
_shear.x, 1.0
);
}
shear(vec2(0.5, 0.0)) * coordinates.xy で座標がX方向にずれて coordinates.x += coordinates.y * 0.5 になる。
| 変形前 | 変形後 |
|---|---|
 |
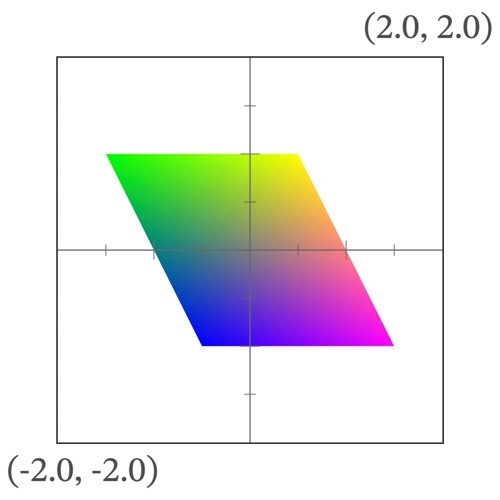 |
shear(vec2(0.0, 0.5)) * coordinates.xy で座標がY方向にずれて coordinates.y += coordinates.x * 0.5 になる。
| 変形前 | 変形後 |
|---|---|
 |
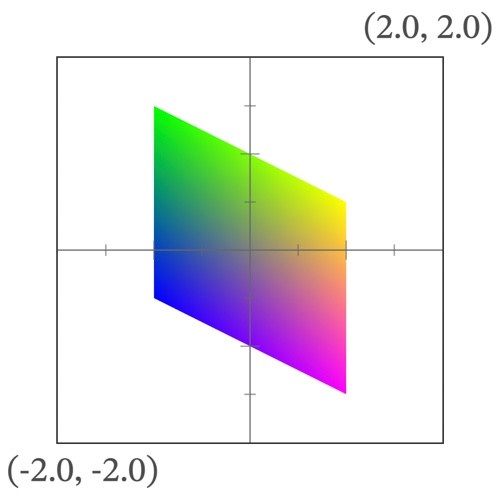 |