🎃

AtCoder 競プロ典型 90 問個人的メモ

2021/07/28に公開

Python

競技プログラミング

AtCoder

tech

https://atcoder.jp/contests/typical90
上記コンテストの解説で、自分にとって良く分からなかった部分を補足します。
随時更新される予定

015 - Don't be too close(★6)

計算量の見積もりに調和級数の部分和が必要。

各クエリで選べるボールの最大数は $\lceil N/k\rceil$ となる。
各クエリでボールを選ぶ個数毎に場合の数を $O(1)$ で求めるとする(各クエリ毎に $O(\lceil N/k\rceil)$ )と、全体の計算量は $O(\sum_{k=1}^N\lceil N/k\rceil)$ となる。
これは天井関数を外した $\sum_{k=1}^NN/k$ よりも明らかに小さい。
調和数は $\sum_{k=1}^N1/k\leq 1+\ln N$ が成り立つので、 $O(\sum_{k=1}^N\lceil N/k\rceil)\leq O(N\ln N)$ となり、十分に高速と分かる。
各クエリでボールをa個選ぶ場合の数は $_{N-(k-1)(a-1)}C_a$ で求まる。

def combination(n: int, r: int):
    return fact[n] * pow(fact[n - r] * fact[r], MOD - 2, MOD) % MOD


N = int(input())
MOD = 10 ** 9 + 7

# LUT
fact = [1]
for i in range(N):
    fact.append(fact[-1] * (i + 1) % MOD)

ans = []
for k in range(1, N + 1):
    max_pick = -(-N // k)
    res = 0
    for i in range(1, max_pick + 1):
        res += combination(N - (k - 1) * (i - 1), i)
        res %= MOD
    ans.append(res)

print(*ans, sep="\n")

参考

公式解説

調和級数

https://manabitimes.jp/math/627

021 - Come Back in One Piece(★5)

SCC(Strongly Connected Components, 強連結成分分解)をする。

テキトーな頂点からDFSをして帰りがけの順(post order)を記録する。
これを全ての頂点を記録するまで行う。
この操作は強連結成分をトポロジカルソートしている。(それぞれの強連結成分を1つの頂点とするとDAGになっている)
辺を逆向きにして、記録した頂点の最後の点を始点としてDFSをする。
この時に到達できる頂点同士が1つの強連結成分になっている。
未到達の点の内で記録した頂点の最後の点を始点として再びDFS。これを繰り返すことで全ての強連結成分が分かる。

この問題では各強連結成分ごとに強連結成分の大きさを $S$ とした時、二項係数 $_SC_2$ を計算してその総和を求めればおｋ。

from math import factorial
from sys import setrecursionlimit

setrecursionlimit(10 ** 7)


def comb(n, k):
    if n < k:
        return 0
    return factorial(n) // (factorial(k) * factorial(n - k))


def rec(now: int):
    if seen[now]:
        return
    seen[now] = 1
    for n_node in edge[now]:
        if seen[n_node]:
            continue
        rec(n_node)
    post_order.append(now)
    return


def rec_re(now: int):
    global cnt
    if seen[now]:
        return
    seen[now] = 1
    for n_node in re_edge[now]:
        if seen[n_node]:
            continue
        rec_re(n_node)
    cnt += 1
    return


N, M = map(int, input().split())
edge = [[] for _ in range(N)]
re_edge = [[] for _ in range(N)]
for _ in range(M):
    x, y = map(lambda n: int(n) - 1, input().split())
    edge[x].append(y)
    re_edge[y].append(x)

# SCCのために強連結成分同士のトポロジカルソートをする
# つまり、テキトーな頂点からDFSをして帰りがけの順を記録する。これを全ての頂点を記録するまで行う
seen = [0] * N
post_order = []
for i in range(N):
    rec(i)

ans = 0
seen = [0] * N
for i in post_order[::-1]:
    cnt = 0
    rec_re(i)
    # 現在のatcoderのpypyだとmath.combが使えないのでcomb関数は自作
    ans += comb(cnt, 2)

print(ans)

参考

とてもわかり易いと思った

036 - Max Manhattan Distance(★5)

$|x|=max(x,-x)$ とすると、マンハッタン距離 $dist(a,b)$ の式は以下のように変形できる。

\begin{aligned} dist(a,b)&=|x_a-x_b|+|y_a-y_b|\\ &=max(x_a-x_b,\ -(x_a-x_b))+max(y_a-y_b,\ -(y_a-y_b))\\ &=max(x_a-x_b+y_a-y_b,\ x_a-x_b-(y_a-y_b),\ -(x_a-x_b)+y_a-y_b,\ -(x_a-x_b)-(y_a-y_b))\\ &=max(x_a+y_a-(x_b+y_b),\ x_a-y_a-(x_b-y_b),\ -(x_a-y_a)+x_b-y_b,\ -(x_a+y_a)+x_b+y_b) \end{aligned}

各 $i$ での $x_i+y_i$ の集合を $S_p$ 、 $x_i-y_i$ の集合を $S_m$ とする。
各クエリで与えられる点が $(x_q,y_q)$ とすると、求めたいマンハッタン距離の最大値 $dist_{max}$ は、以下のように計算できる。
右辺の各項が最大化するように集合から点を選ぶのが最適なので、正負に応じて集合の最小値か最大値を使う。

dist_{max}=max(x_q+y_q-min(S_m),\ x_q-y_q-min(S_m),\ -(x_q-y_q)+max(S_m),\ -(x_q+y_q)+max(S_p))

これは $S_p,S_m$ の最大値と最小値を求めておけば $O(1)$ で求まる。
従って、事前計算に $O(N)$ で各クエリ当たり $O(1)$ で計算できるので十分高速に解ける。

N, Q = map(int, input().split())
S_p, S_m = [], []
for _ in range(N):
    x, y = map(int, input().split())
    S_p.append(x + y)
    S_m.append(x - y)

p_min, p_max = min(S_p), max(S_p)
m_min, m_max = min(S_m), max(S_m)

for _ in range(Q):
    q = int(input())
    pi = S_p[q - 1]
    mi = S_m[q - 1]
    print(max(pi - p_min, mi - m_min, -mi + m_max, -pi + p_max))

参考

042 - Multiple of 9(★4)

ある数 $X$ の各桁の数字の和が9の倍数なら、その数は9の倍数。
よってKが9の倍数ならば条件を満たす解が存在し、Kが9の倍数で無いならば解は存在しないと分かる。
従って2つの条件の内、 $X$ の各桁の数字の和のみを考えればおｋ
$K$ 個のボールにいくつかの仕切りを入れる場合の数を勘定する。
仕切りの間隔は1~9とする。
この時 $dp[i]:=各桁の数字の和がiの場合の数$ とする。
$dp[i]=\sum_{j=0}^9dp[i-j]$ なので、遷移は $O(10)$ でおｋ。

各倍数の性質(公式解説より)

2の倍数
1の位が2,4,6,8,0(偶数)
3の倍数
各桁の数字の和が3の倍数
4の倍数
下2桁が4の倍数
5の倍数
1の位が0,5
8の倍数
下3桁が8の倍数
9の倍数
各桁の数字の和が9の倍数
11の倍数
(奇数桁目の数字の和)-(偶数桁目の数字の和)が11の倍数

K = int(input())
MOD = 10 ** 9 + 7

if K % 9:
    print(0)
    exit()

dp = [0] * (K + 1)
dp[0] = 1
for i in range(1, K + 1):
    dp[i] = sum(dp[max(0, i-9):i]) % MOD

print(dp[-1])

参考

公式解説

073 - We Need Both a and b(★5)

木dp
dp[i][j]を頂点iの部分木の辺を削除した時、iを含む連結成分が状態j(0:aのみ,1:bのみ,2:a,b両方含む)でそれ以外の連結成分が両方の文字を含む場合の数とする。

from sys import setrecursionlimit

setrecursionlimit(10 ** 7)


def rec(now: int, last: int = -1):
    dp[now][C[now]] = 1
    dp[now][2] = 1
    for n_node in edge[now]:
        if n_node == last:
            continue
        rec(n_node, now)
        """
        どちらか一方の頂点しか含まない場合(j = 0, 1)
        頂点nowとnowに隣接する頂点n_nodeを結ぶ辺を削除しない場合と削除する場合が考えられる
        削除しない場合はn_node以下の部分木がnowと同じ文字のみから成っている必要がある
        削除する場合はn_node以下の部分木が両方の文字を含む必要がある
            削除後の部分木は問題の条件を満たすように考えているから
        """
        for i in (0, 1):
            # 削除しない場合
            res = dp[n_node][i]
            # 削除する場合
            res += dp[n_node][2]
            dp[now][i] *= res
            dp[now][i] %= MOD
        """
        両方の文字を含む場合(j = 2)
        削除しない場合はn_node以下の部分木にnowと別の頂点が含まれている必要がある
            つまり、全ての場合からC[now]と同じ文字のみから成る場合を除いた場合
            dp[now][2](削除☓) = prod(sum(dp[n_node])) - dp[now][C[now]]
        削除する場合はn_node以下の部分木が両方の文字を含む必要がある(dp[n_node][2])
            dp[now][2](削除◯) = prod(dp[n_node][2])
        合わせて、dp[now][2] = prod(sum(dp[n_node]) + dp[n_node][2]) - dp[now][C[now]]
        """
        dp[now][2] *= sum(dp[n_node]) + dp[n_node][2]
        dp[now][2] %= MOD

    dp[now][2] -= dp[now][C[now]]
    dp[now][2] %= MOD
    return dp[now][2]


N = int(input())
C = list(map(lambda a: 1 if a == "a" else 0, input().split()))
edge = [[] for _ in range(N)]
for i in range(N - 1):
    x, y = map(lambda n: int(n) - 1, input().split())
    edge[x].append(y)
    edge[y].append(x)
MOD = 10 ** 9 + 7

dp = [[0] * 3 for _ in range(N)]
print(rec(0))

086 - Snuke's Favorite Arrays(★5)

2進数の論理演算なので各桁は独立に考えることができる(ある桁の論理演算がどうなったとしても他の桁には影響しないから)。
なので、数列 $A$ の各桁ごとに条件1を満たしているかを考える(サンプル1の場合は下図のようになる)。
これは $A$ の各要素を桁ごとにbit全探索して、条件1を満たしている場合の数 $ways$ を数える。
上述の様に各桁は独立しているので、各桁の $ways$ の総積が答えとなる。
$i$ 桁目のbit全探索に $O(2^N)$ 、各bitでのクエリの確認に $O(Q)$ となる。
$A_i<2^{60}$ より $A_i$ は2進数で60桁以下なので全体の計算量は $O(60\times 2^N\times Q)\simeq O(10^6)$ となり十分高速。

fig

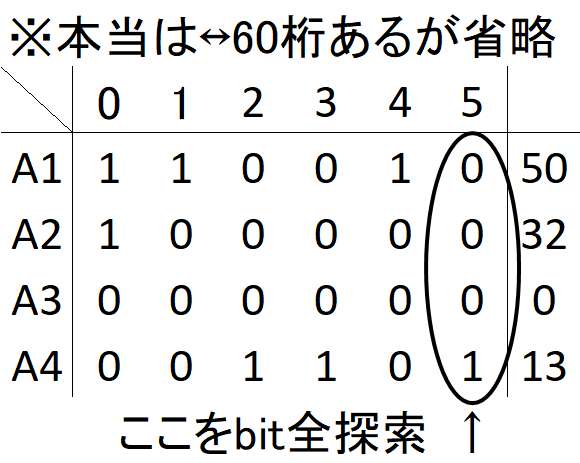
def is_conditon1_ok(B: list, i: int):
    """各Aiの上からi桁目の候補となるbit列Bが全てのクエリを満たしているか？"""
    return all(B[x] | B[y] | B[z] == int(w[i]) for x, y, z, w in query)

def bit_search(i: int):
    """各Aiの上からi桁目をbit全探索"""
    ways = 0
    for bit in range(1 << N):
        bit = list(map(int, f"{bit:0{N}b}"))
        if is_conditon1_ok(bit, i):
            ways += 1
    return ways % MOD


N, Q = map(int, input().split())
query = []
digit_limit = 60
for _ in range(Q):
    x, y, z, w = map(int, input().split())
    # wだけf文字列を使って2進数の文字列にしておく
    query.append((x - 1, y - 1, z - 1, f"{w:0{digit_limit}b}"))
MOD = 10 ** 9 + 7

ans = 1
for i in range(digit_limit):
    ans *= bit_search(i)
    ans %= MOD

print(ans)