AtCoder ARC132 個人的メモ

A - Permutation Grid

問題文と制約にもあるが、$R$と$C$は順列なので$1$から$N$までの数を１つずつ持つ。

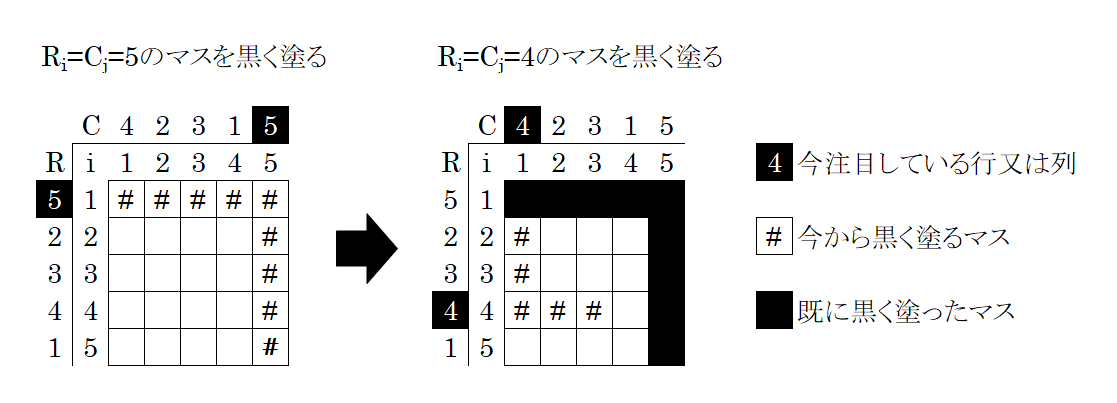
例1の場合について実際に色を塗ってみる。
まず$R_i=5$の行は、行のマス数$n$と黒マスの数$R_i$が等しいので、全てのマスが黒マスになる。
同様に$C_j=5$の列も全てのマスが黒マスになる。
次に$R_i=4$の行を考えると、$C_j=5$となる列の全てのマスを黒く塗ったので、$R_i=4$の行の内の1マスは既に黒く塗られている。
そのため、新たに黒く塗るマスは4つの白マスの内の3つになる。
また、この時の白マスは$1\leq C_j\leq 4$となっている。
ここで$R_i=4$かつ$C_j=1$のマスを黒く塗ると、$C_j=1$の列に$R_i=5$と$R_i=4$の2つの黒マスがあることになり、問題文の制約を満たせない。
よって、$R_i=4$の行で黒く塗れるマスは$C_j=1$のマス以外となる。
同様に$C_j=4$の場合や$R_i<4$の場合も考えると、黒く塗れるマスは$R_i+C_j>n$となるマス$(i,j)$と分かる。

N = int(input())
R = list(map(int, input().split()))
C = list(map(int, input().split()))
Q = int(input())

ans = []
for _ in range(Q):
    r, c = map(lambda n: int(n) - 1, input().split())
    if R[r] + C[c] > N:
        ans.append("#")
    else:
        ans.append(".")

print("".join(ans))

B - Shift and Reverse

数列$P$の先頭と末尾がループしてるとすると、問題文の2つの操作は以下の図の様になる。

数字は数列のインデックス(何番目か)を示す
# 操作前の状態
8 1 2
7   3
6 5 4
# 全体をひっくりかえす
1 8 7
2   6
3 4 5
# 先頭の項を末尾に移動させる
1 2 3
8   4
7 6 5

この図から、操作によって各要素の順番を変えることはできず、数列の先頭を任意の要素に変更することしかできないと分かる。
制約により与えられる$P$はこの操作のみで昇順(小さい順)の順列に並び替えられることになっているから、$P$は1の要素からループの時計回りか反時計回りに昇順になっているはずと分かる。
したがって以下のように場合分けして解けばおｋ。

• $P_i=1$から時計回りに昇順になっている場合($P_{i+1}=2$の場合)
  $P=(4, 5, 1, 2, 3)$のようになっているので、以下の2つのどちらかが答え。

  • 2つ目の操作のみによって1よりも前の要素を全て末尾に移動させる場合(今の$P$だと2回操作)
  • 最初に反転し、その後1よりも前の要素と1を全て末尾に移動させて、最後に再び反転する場合(5回)
    $P=(4, 5, 1, 2, 3)$の場合だと$1,2,3$を移動させる。

• $P_i=1$から反時計回りに昇順になっている場合(P_{i+1}!=2の場合)
  $P=(3, 2, 1, 5, 4)$のようになっている

  • 2つ目の操作によって1よりも前の要素と1を全て末尾に移動させて、最後に再び反転する場合(4回)
  • 最初に反転し、その後1よりも前の要素を全て末尾に移動させる場合(3回)

N = int(input())
P = list(map(int, input().split()))

i = P.index(1)
j = (i + 1) % N
# 小さい順になっている場合
if P[j] == 2:
    ans = min(i, N - i + 2)
# 大きい順になっている場合
else:
    ans = min(j + 1, 1 + N - j)

print(ans)