😎

AtCoder ABC220 個人的メモ

2021/09/27に公開

Python

競技プログラミング

AtCoder

tech

所感

入水!!
やったぜ
abc220score

A - Find Multiple

A, B, C = map(int, input().split())

for i in range(1, 10 ** 3):
    if A <= C * i <= B:
        print(C * i)
        exit()

print(-1)

B - Base K

K = int(input())
# int(x,K)でK進数の文字列xを10進数に変換できる
A, B = map(lambda x: int(x, K), input().split())

print(A * B)

C - Long Sequence

N = int(input())
A = list(map(int, input().split()))
X = int(input())

sum_A = sum(A)
multi = X // sum_A
now_sum = sum_A * multi
ans = len(A) * multi
for a in A:
    if now_sum > X:
        print(ans)
        exit()
    now_sum += a
    ans += 1

print(ans)

D - FG operation

N = int(input())
A = list(map(int, input().split()))
MOD = 998244353

# dp[i][j]:=i番目までのAiでK=jとなる場合の数
dp = [[0] * (10) for _ in range(N)]
dp[0][A[0]] = 1
for i in range(1, N):
    a = A[i]
    for j in range(10):
        dp[i][(a + j) % 10] += dp[i - 1][j]
        dp[i][(a + j) % 10] %= MOD
        dp[i][(a * j) % 10] += dp[i - 1][j]
        dp[i][(a * j) % 10] %= MOD

print(*dp[-1], sep="\n")

F - Distance Sums 2

$f(i)=\sum_{j=1}^Ndis(i,j)$ とする。
とりあえず $i=1$ として $f(1)=\sum_{j=1}^Ndis(1,j)$ を考えてみる。
これは頂点1からdfsなりbfsをすれば $O(N)$ で求められる(dfs,bfsの計算量は頂点の個数と辺の個数の和)。
これを全ての頂点から求めると全体で $O(N^2)$ となってtleする。
なので高速化したい。

$f(1)$ を求めた後に別の頂点で $f(i)$ を求める時、 $f(1)$ との差分が分かれば新たにグラフの探索する必要は無いので高速化できそう。
なので下図のようにグラフで頂点 $i$ が変化したときの $f(i)$ の変化を考えてみる。
頂点横の数字は $dis(i,j)$ を示している。

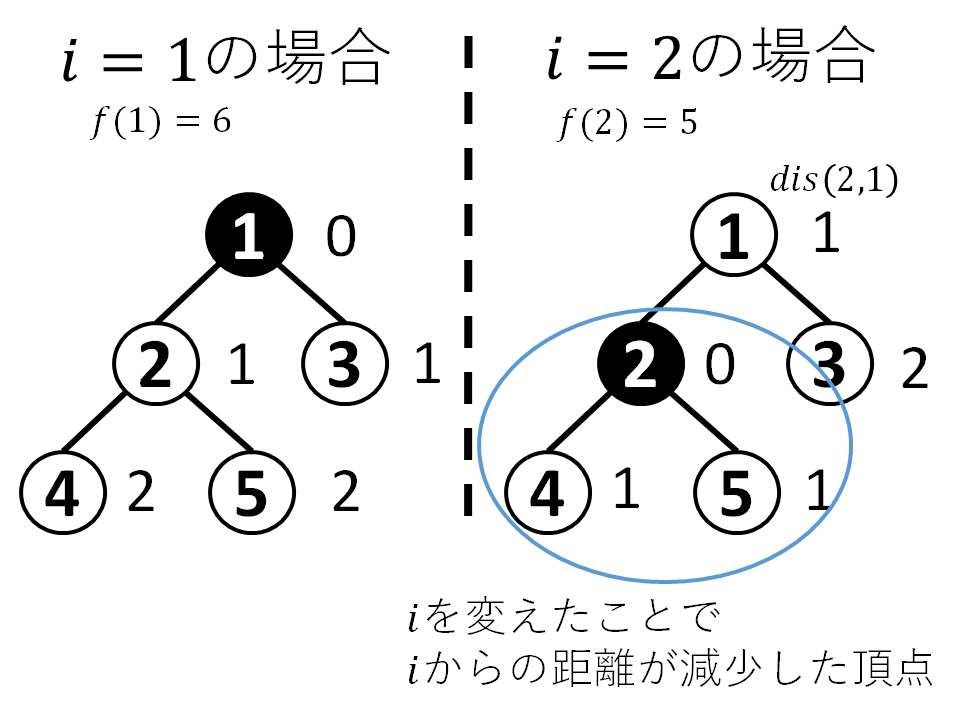
abc220f

すると以下のことが分かる。

$i$ が頂点 $a$ から $a$ と隣接している頂点 $b$ へ変化した時、 $dis(b,j)$ は $dis(a,j)$ から以下のように変化する。

$a$ と $b$ を結ぶ辺を除いた場合に頂点 $j$ が $a$ と連結な場合(水色の丸で囲まれていない頂点)
$dis(b,j)=dis(a,j)+1$
$a$ と $b$ を結ぶ辺を除いた場合に頂点 $j$ が $b$ と連結な場合(水色の丸で囲んだ頂点)
$dis(b,j)=dis(a,j)-1$

つまり、 $f(b)$ は $f(a)$ と $b$ の部分木の大きさが分かれば $O(1)$ で求めることができる。
( $b$ を含まない $a$ の連結成分の大きさは、全ての頂点数を $N$ とすると $N-(bの部分木の大きさ)$ で求まる)

これより以下の手順で答えを求めることができる。

頂点1を根とするdfsをして各頂点の部分木の大きさを求める。 $O(N)$
$f(1)=\sum_{j=1}^Ndis(1,j)$ を求める。 $O(1)$
↑で求めた部分木の大きさから求めることができる。
bfsで頂点1に隣接する頂点から順に $f(i)=\sum_{j=1}^Ndis(i,j)$ を求める。 $O(N)$

よって全体で $O(N)$ となり十分高速に答えを求めることができる。

from collections import deque
from sys import setrecursionlimit

setrecursionlimit(10 ** 7)


def search_num_child(now: int):
    """0を根とした木において、頂点now以下の頂点数(頂点nowとその子の数)をdfsで求める"""
    if num_child[now]:
        return num_child[now]
    num_child[now] = 1
    for n_node in edge[now]:
        if num_child[n_node]:
            continue
        num_child[now] += search_num_child(n_node)
    return num_child[now]


N = int(input())
edge = [[] for _ in range(N)]
for _ in range(N - 1):
    x, y = map(lambda n: int(n) - 1, input().split())
    edge[x].append(y)
    edge[y].append(x)

# num_child[i]:=頂点0を根としたiの部分木の大きさ(iを含む)
num_child = [0] * N
search_num_child(0)
dis_from_zero = sum(num_child) - N

# 0を根としてbfsで高さが低い頂点から(0に近い頂点から)ansを求めていく
ans = [dis_from_zero] * N
seen = [0] * N
queue = deque([(0, 0)])
while queue:
    now, parents = queue.popleft()
    seen[now] = 1

    if now:
        res = ans[parents]
        # 移動後の頂点の子ノードは距離が減る
        res -= num_child[now]
        # 移動後の頂点の親ノードは距離が増える
        res += N - num_child[now]
        ans[now] = res

    for n_node in edge[now]:
        if seen[n_node]:
            continue
        queue.append((n_node, now))

print(*ans, sep="\n")