AtCoder ARC124 個人的メモ

所感

abc3完で青パフォ
やったぜ

A - LR Constraints

カードに書き込める数の制約は以下のように言える。

• $c_i="L"$の時
  インデックス$k_i$の数字はi。$k_i$より後のカードから数字iを書き込めるようになる。
• $c_i="R"$の時
  インデックス$k_i$の数字はi。$k_i$より後のカードには数字iを書き込めなくなる(それ以前には書き込める)。

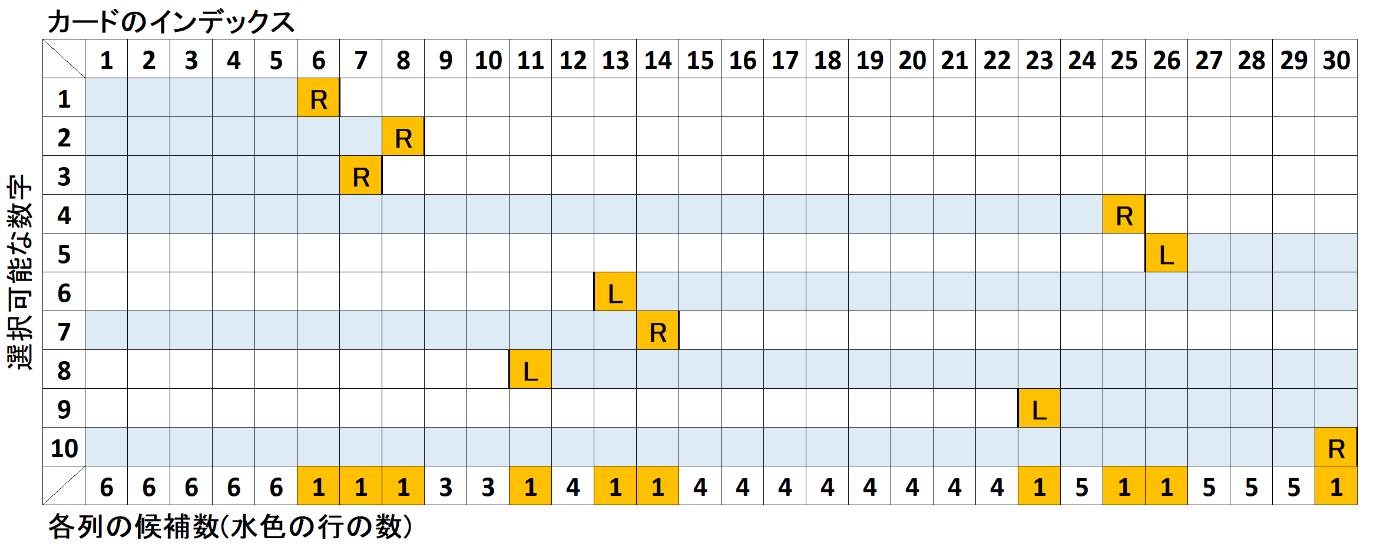
サンプル2の場合を図にすると下図のようになる。
図の下の「各列の候補数」の総積が答えになるので、これを実装すればおｋ。

N, K = map(int, input().split())
constraints = [0] * (N + 1)
can_num = 0
for _ in range(K):
    c, k = input().split()
    constraints[int(k)] = c
    if c == "R":
        can_num += 1
MOD = 998244353

ans = 1
# カードを左端から右へ向けて順に見ていく
for i in range(1, N + 1):
    # 今のカードのインデックスに制約があるか？無いか？をチェック
    if constraints[i]:
        # 制約があるなら今のカードのインデックスの数は既に指定されている(候補が１つしか無い)
        # 加えて候補となる数の種類が変化する
        if constraints[i] == "L":
            can_num += 1
        else:
            can_num -= 1

    # 今のカードのインデックスでの制約が無いなら候補数を掛け算する
    else:
        ans *= can_num
        ans %= MOD

print(ans)

B - XOR Matching 2

適当な$a$の要素$a_i$に対して全ての$b$の要素とXORを取る。
その結果を集合$S_i$とする。
良い数となる$x$は全てこの集合$S_i$に含まれている。
他の$a$の要素に対しても同様に$b$とのXORを取り、その結果を集合とする。
すべての集合に共通している要素が良い数となる。

ってやったら通った。

from functools import reduce

N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

candidates = (set(a ^ b for b in B) for a in A)
ans = reduce(lambda a, b: a & b, candidates)

print(len(ans), *sorted(ans), sep="\n")

C - LCM of GCDs

https://atcoder.jp/contests/arc124/editorial/2328

from math import gcd

N = int(input())
cards = [list(map(int, input().split())) for _ in range(N)]  # 整数を入力

# i番目までの数で作れる最大公約数の組の集合
seen_pairs = [set() for _ in range(N)]
seen_pairs[0] = {" ".join(map(str, sorted(cards[0])))}
for i in range(1, N):
    c, d = cards[i]
    for pair in seen_pairs[i - 1]:
        a, b = map(int, pair.split())
        seen_pairs[i].add(" ".join(map(str, sorted([gcd(a, c), gcd(b, d)]))))
        seen_pairs[i].add(" ".join(map(str, sorted([gcd(a, d), gcd(b, c)]))))

ans = 0
for pair in seen_pairs[-1]:
    a, b = map(int, pair.split())
    ans = max(ans, a * b // gcd(a, b))

print(ans)

D - Yet Another Sorting Problem

サンプル2を考える。
$i\not ={P_i}$の要素はインデックスが$j=P_i$の要素と交換したい。
$j$の要素はインデックスが$k=P_j$の要素と交換したい。
ということで、各$P$を頂点として交換したい間(各$i$と$P_i$間)に辺を張ってみると、下図の様にいくつかの連結成分に分かれることが分かる。
④の場合の最小操作回数は、連結成分の反対側である左側のテキトーな要素を使って10と8を入れ替える。

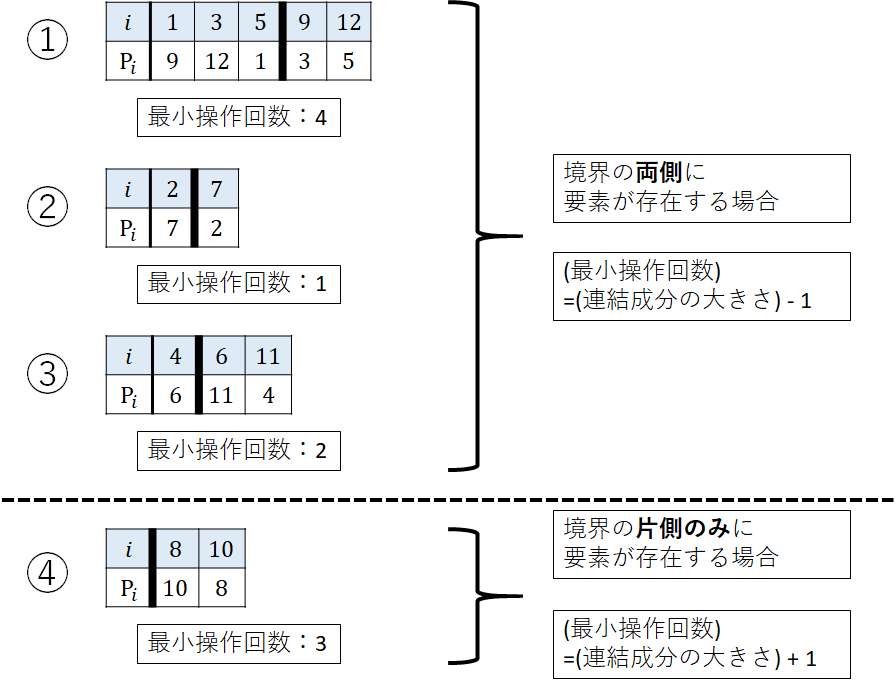
また下図の様に境界の片側のみに要素が存在する連結成分が境界の両側にある場合もある。
この場合は下図の様に操作をすることで、$(2+1)+(2+1)=6$の操作回数から
$1+(2+2-1)=4$の操作回数に減らすことができる。
つまりそれぞれの連結成分の大きさを$|a|,|b|$とした時、$(|a|+1)+(|b|+1)=|a|+|b|+2$から$1+(|a|+|b|-1)=|a|+|b|$に変化させる事ができる。

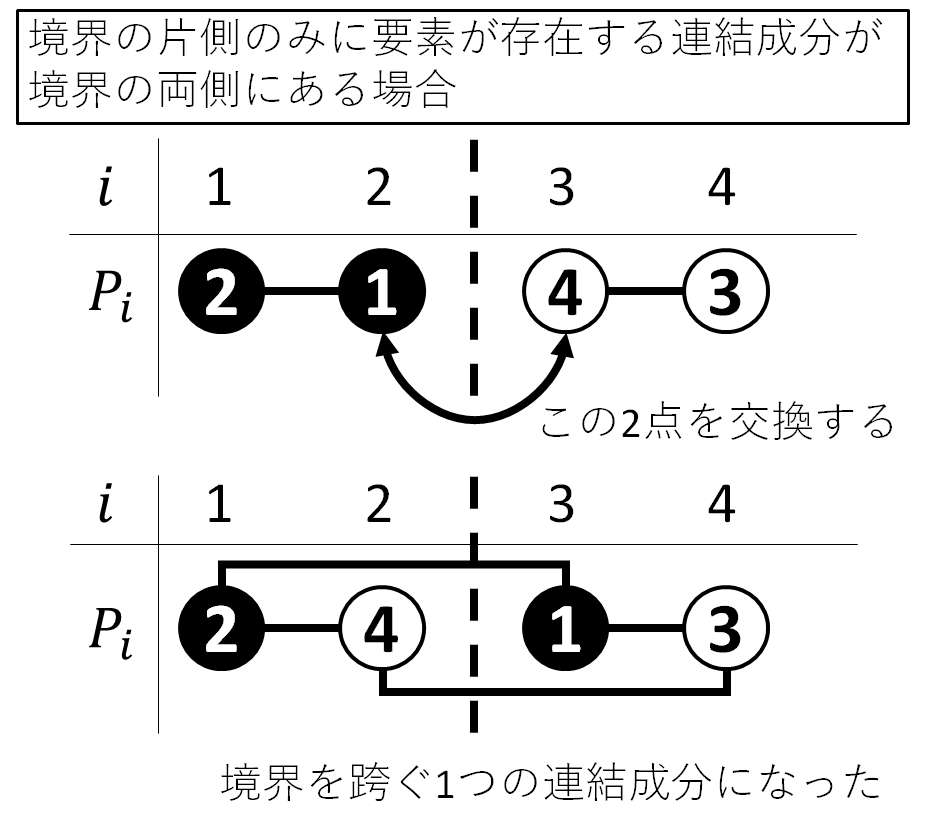
というわけで以下を実装すれば良さそう。

1. union-findで$i\leftrightarrow P_i$間に辺を張り、連結成分を調べる。その際に連結成分が境界を跨いでいるかも調べる。

2. 以下の場合分けに基づいて答えに操作回数を加算する。

   • 連結成分の大きさが1の場合
     既に$i=P_i$となっているので操作不要
   • 連結成分が境界を跨いでいる場合
     $(操作回数)=(連結成分の大きさ)-1$
   • 連結成分が境界を跨いでいない場合
     これらの連結成分が境界の左右どちらに存在するかを勘定
     →最後に境界の反対側の連結成分とペアを作れない成分の数を答えに加算

公式解説の様に、全ての連結成分の個数を$K$、境界の左側にのみ要素がある連結成分の個数を$R$、境界の右側の連結成分を$B$とすると、答えは$N+M-(K-R-B)+|R-B|$で求めている。

union-find

class UnionFind:
    """Union-Find(素集合データ構造(disjoint-set data structure)に対しての操作)"""

    def __init__(self, n: int):
        """
        Constructer(Initialize parameter in this class)

        Parameters
        ----------
        n : int
            Number of node

        Yields
        -----
        root : list
            When value is postive, express root of the node.
            When it is negative, express this node is root and size of set.
        """

        self.root = [-1] * n

    def find(self, x: int) -> int:
        """
        Search root of node x

        Parameters
        ----------
        x : int
            node x

        Returns
        -------
        x : int
            Root of node x
        """

        if self.root[x] < 0:
            return x
        self.root[x] = self.find(self.root[x])
        return self.root[x]

    def unite(self, x: int, y: int) -> bool:
        """
        Unite two set including node x and node y into one set.

        Parameters
        ----------
        x, y : int
            Node number

        Returns
        -------
        unite_result : bool
            False : Already two node include same set.
            True  : United
        """

        x = self.find(x)
        y = self.find(y)
        if x == y:
            return False
        if self.root[x] > self.root[y]:
            x, y = y, x
        self.root[x] += self.root[y]
        self.root[y] = x
        return True

    def is_same(self, x: int, y: int) -> bool:
        """
        Determine if x and y are in same set.

        Parameters
        ----------
        x, y : int
            Node number

        Returns
        -------
        result : bool
            Determining result
        """

        return self.find(x) == self.find(y)

    def size(self, x: int) -> int:
        """
        Return size of set including node x.

        Parameters
        ----------
        x : int
            Node number

        Returns
        -------
        Size of set : int
        """

        return self.root[self.find(x)] * -1

N, M = map(int, input().split())
P = list(map(lambda n: int(n) - 1, input().split()))

union = UnionFind(N + M)
# iを含む連結成分に境界の両側の要素が含まれているか？
is_crossed = [0] * (N + M)
# 境界を跨いでいる辺の端点をメモ
cross_edges = set()
# iとPi間に辺を張る
for i, p in enumerate(P):
    union.unite(i, p)
    if min(i, p) < N and N <= max(i, p):
        cross_edges.add(union.find(i))
# 境界を跨いでいる辺の端点を含んでいる連結成分から、is_crossed[i]が分かる
for i in range(N + M):
    if any(union.is_same(i, j) for j in cross_edges):
        is_crossed[i] = 1

ans = 0
# 全ての要素が境界のどちらかに偏っている連結成分の数
left_only = 0
right_only = 0
for node in range(N + M):
    # 根以外のインデックスと既にインデックスがあっているもの(操作不要の奴)は除外
    if union.root[node] >= -1:
        continue
    # 境界を跨ぐ連結成分は(連結成分の大きさ)-1の操作回数
    if is_crossed[node]:
        ans += union.size(node) - 1
    # そうでない場合は(連結成分の大きさ)+1の操作回数だが、
    # 左側のみの連結成分aと右側のみの奴bのテキトーな要素を入れ替えることで、
    # 新しい連結成分a+bは境界を跨ぐことになり、連結前よりも操作回数が少なくなる
    else:
        ans += union.size(node)
        if node < N:
            left_only += 1
        else:
            right_only += 1

ans += abs(left_only - right_only)

print(ans)

参考

公式解説
https://atcoder.jp/contests/arc124/editorial/2337