🤖

AtCoder ABC210 個人的メモ

2021/07/18に公開

Python

競技プログラミング

AtCoder

tech

A - Cabbages

N, A, X, Y = map(int, input().split())

if N <= A:
    print(N * X)
else:
    print(A * X + (N - A) * Y)

B - Bouzu Mekuri

問題文通りにシミュレーションするだけ。
下のコードのほうが簡潔で良いと思った。

N = int(input())
S = input()

for i, s in enumerate(S):
    if s == "0":
        continue
    if (i + 1) % 2:
        print("Takahashi")
    else:
        print("Aoki")
    break

N = int(input())
S = input()

if (S.index("1") + 1) % 2:
    print("Takahashi")
else:
    print("Aoki")

C - Colorful Candies

全てのiで、区間 $[i,i+K-1]$ に含まれるキャンディの種類が分かれば、その最大値が答え。
iからi+1へ遷移する時、区間は1つ正の方向へ移動するため、区間からiが外れてi+Kが入る。
これを実装すれば各i辺りO(1)でキャンディの種類を求められそう。

from collections import Counter

N, K = map(int, input().split())
C = list(map(int, input().split()))

cnt = Counter()
now = 0
ans = 0
for i, c in enumerate(C):
    if i >= K:
        cnt[C[i - K]] -= 1
        if cnt[C[i - K]] == 0:
            now -= 1
    
    cnt[c] += 1
    if cnt[c] == 1:
        now += 1

    ans = max(ans, now)

print(ans)

まず線路のコストが絶対値で表されているため、この絶対値を外したい。
この絶対値の正負は2つの駅の位置関係によって決まる。
2つの駅を区別して、それぞれの座標を $(i,j),(i',j')$ (2点の座標は同一でない)とすると下図の様に4通りがある。
この問題では2つの駅を区別する必要は無いのでa=c、b=dとして2通りのみを考えればおｋ。
d_fig
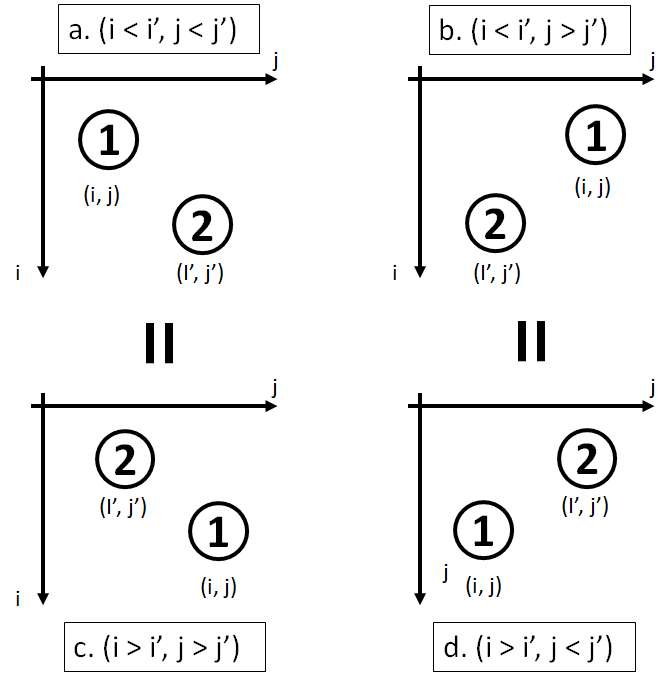
以上より、とりあえずaの場合( $i\leq i',\ j\leq j'$ )を考える。
この時のコストは、問題文で与えられた式を絶対値を外してから整理すると以下のように表される。

\begin{aligned} cost &=A_{i,j} + A_{i',j'} + C(|i-i'| + |j-j'|)\\ &=A_{i,j} + A_{i',j'} + C(i'-i + j'-j)\\ &=A_{i,j} - C(i + j) + A_{i',j'} + C(i'+ j')\\ \end{aligned}

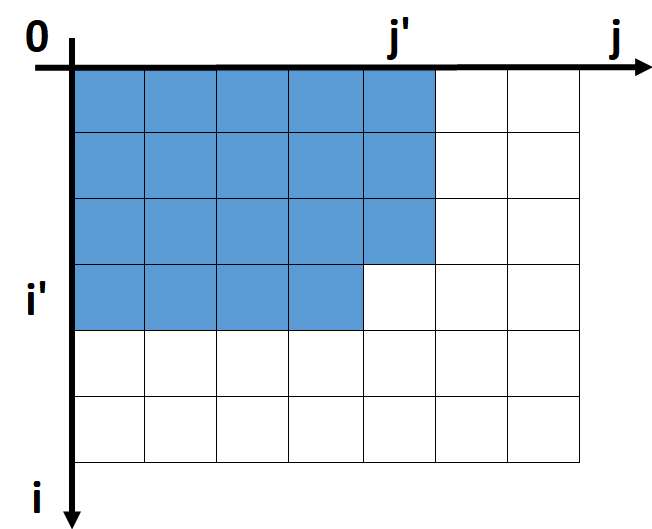
以上の式より、一方の点 $(i',j')$ を固定した時の最小コストは以下のように表される。

\min_{i\leq i'\land j\leq j'\land (i,j)\not ={(i',j')}} (A_{i,j} - C(i + j)) + A_{i',j'} + C(i'+ j')

よって各 $(i',j')$ での最適値は、下図の青い範囲における $A_{i,j} - C(i + j)$ の最小値が分かれば求まる。
これは $(0,0)$ から $(H-1,W-1)$ に向けて累積最小値を求めておけば、各 $(i',j')$ あたり $O(1)$ で求まる。
$(i',j')$ は $HW$ 通りあるから、全体で $O(HW)$ で求まるので、これで $i\leq i',\ j\leq j'$ の場合は解けそう。
d_fig2
もう1つの $i\leq i',\ j\geq j'$ の場合を考える。
このbの場合はaの場合を左右反転したものだということが最初の図から分かるので、Aを左右反転してaの場合を同じ様にやれば解けそう。
しかし、コストの式が少し異なる。
これは $i$ と $i'$ 、 $j$ と $j'$ の大小関係がaの場合と異なることによる。
なので、以下のように色変系の際に絶対値を外した際の正負が変わっている。

\begin{aligned} cost &=A_{i,j} + A_{i',j'} + C(|i-i'| + |j-j'|)\\ &=A_{i,j} + A_{i',j'} + C(i'-i + j-j')\ \\ &=A_{i,j} - C(i - j) + A_{i',j'} + C(i'- j')\\ \end{aligned}

よって、この場合における最適解は以下のように表される。

\min_{i\leq i'\land j\leq j'\land (i,j)\not ={(i',j')}} (A_{i,j} - C(i - j)) + A_{i',j'} + C(i'- j')

で、2つの場合の全ての $(i',j')$ における最小のコストが答えとなる。

H, W, C = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]
INF = 10 ** 18

ans = INF
for is_rev in (0, 1):
    # 番兵のために配列を縦横に1マスずつ多く取る
    # (i,j)を含むここよりも左上の区間でのA[i][j] - C * (i + j)の最小値
    cummin = [[INF] * (W + 1) for _ in range(H + 1)]
    for i in range(H):
        for j in (range(W - 1, -1, -1) if is_rev else range(W)):
            if is_rev:
                cummin[i][j] = min(cummin[i - 1][j],
                                   cummin[i][j + 1],
                                   A[i][j] - C * (i - j))
            else:
                cummin[i][j] = min(cummin[i - 1][j],
                                   cummin[i][j - 1],
                                   A[i][j] - C * (i + j))

    for i in range(H):
        for j in (range(W - 1, -1, -1) if is_rev else range(W)):
            if is_rev:
                blue_area_min = min(cummin[i - 1][j], cummin[i][j + 1])
                ans = min(ans, blue_area_min + A[i][j] + C * (i - j))
            else:
                blue_area_min = min(cummin[i - 1][j], cummin[i][j - 1])
                ans = min(ans, blue_area_min + A[i][j] + C * (i + j))

print(ans)

公式解説で解説acしたコード(ほぼ↑のと一緒)

H, W, C = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]  # 整数を入力
INF = 10 ** 18

ans = INF
# 左右反転して同じ操作を2回するが、実際にAを左右反転するとtleするので、走査順のみを左右反転
for is_rev in (0, 1):
    # dp1[i][j]:=(i,j)を含む(i,j)よりも左上のどこかに始点を置いた時、(i,j)に達するまでの最小コスト
    # 番兵を用いるため(遷移する時にグリッドの外へ出るかの判定をサボるため)にdp配列はHとWよりも大きい値を用いる
    dp1 = [[INF] * (W + 1) for _ in range(H + 1)]
    for i in range(H):
        for j in (range(W - 1, -1, -1) if is_rev else range(W)):
            # (i,j)を始点とする場合
            res = A[i][j]
            # (i+1,j)(現在地の上のマス)から線路を建設してきた場合
            res = min(res, dp1[i - 1][j] + C)
            # 横から線路を建設してきた場合(is_rev = 1: 右から, is_rev = 0: 左から)
            if is_rev:
                res = min(res, dp1[i][j + 1] + C)
            else:
                res = min(res, dp1[i][j - 1] + C)
            dp1[i][j] = res

    # dp2[i][j]:=(i,j)を終点とした時の最小コスト
    dp2 = [[INF] * (W + 1) for _ in range(H + 1)]
    for i in range(H):
        for j in (range(W - 1, -1, -1) if is_rev else range(W)):
            res = INF
            # 上から線路を建設してきた場合
            res = min(res, dp1[i - 1][j] + C + A[i][j])
            # 横から線路を建設してきた場合
            if is_rev:
                res = min(res, dp1[i][j + 1] + C + A[i][j])
            else:
                res = min(res, dp1[i][j - 1] + C + A[i][j])
            dp2[i][j] = res

        ans = min(ans, *dp2[i])
    # print(*dp1, sep="\n", end="\n\n")
    # print(*dp2, sep="\n", end="\n\n")

print(ans)

参考

公式解説

AtCoder ABC210 個人的メモ

A - Cabbages

B - Bouzu Mekuri

C - Colorful Candies

D - National Railway

参考

Discussion