💭

AtCoder ABC209 個人的メモ

2021/07/11に公開

Python

競技プログラミング

AtCoder

tech

所感

abcd4完
d問題全然分かんなくて、もうだめだぁと思ったけどなんとかacできた。
e問題はacはできなかったけど考察→実装がdiffの割には結構できてたと思う。
score

A - Counting

$A\leq B$ なら $B-A+1$ で、そうでないならば $0$

A, B = map(int, input().split())

ans = max(0, B - A + 1)
print(ans)

B - Can you buy them allb

問題文通りに偶数番目の商品を1円引きにした後に総和を取ればおｋ

実装で偶数と奇数を間違えて1wa

N, X = map(int, input().split())
A = list(map(int, input().split()))

for i in range(1, N, 2):
    A[i] -= 1

if X >= sum(A):
    print("Yes")
else:
    print("No")

入力例2を考える。
$A_1$ は $1\leq A_1\leq 3$ の範囲から選ぶので、3通りの選び方がある。
$A_2$ は $A_1$ と同じ範囲だが、 $A_1$ と同じ数字は選べないので2通りの選び方がある。
同様に $A_3$ では2通り、 $A_4$ では1通りの選び方がある。
よって、全体で $3\times 2\times 2\times 1=12$ 通りの選び方があると分かる。
従って、 $\prod_{i=1}^N C_i-i$ で求まりそう。

しかし、これは $C_i> C_{i+1}$ となる時不成立になる。
$A_i$ で $C_{i+1}$ 以上の数字を選んだかどうかで、 $A_{i+1}$ として選べる数字の個数が変化するから。
これを回避するために $C$ を昇順でソートする。
これで、さっきの式で答えが求まる。

N = int(input())
C = list(map(int, input().split()))
MOD = 10 ** 9 + 7

C.sort()
ans = 1
for i, c in enumerate(C):
    ans *= c - i
    ans %= MOD

print(ans)

D - Collision

0を根として各頂点の深さを求める
各頂点間の差の偶奇が解

2頂点間の最短距離の偶奇が分かれば良いから、事前にワーシャルフロイドすれば良さそうと思ったけど、 $N\leq 10^5$ なのでTLEする。
紙で考えてたら、各頂点の深さの差の偶奇を見れば良さそうと思って投げたらacした。

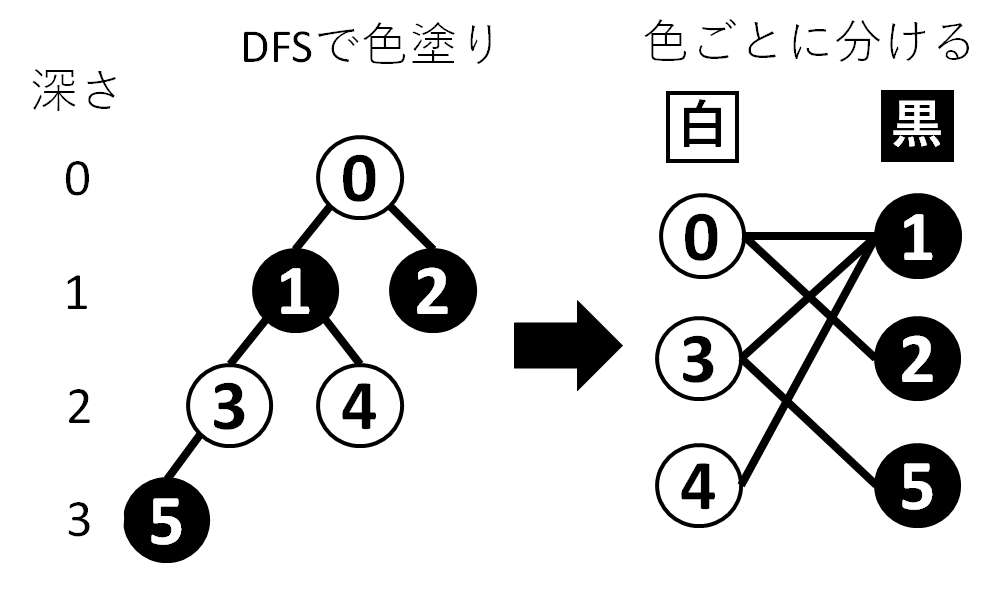
これは木が2部グラフだから。
木の全ての頂点を、白黒2色のみを使って隣接する頂点は異なる色で塗るというルールで塗ることを考える(頂点彩色)。
これは根からDFSをして、隣接する頂点を異なる色で塗っていけば達成できる。
この時、各頂点の色は根とした頂点から各頂点への距離(深さ)の偶奇によって異なっている。

ここで頂点間の移動距離について色ごとに考える。
ルールによって隣接する頂点は異なる色で塗られているため、頂点間の移動の際に通る頂点の色は必ず白→黒→白→・・・の様に交互になる。
従って、2つの頂点の色によって以下のように場合分けされる。

同じ色：両頂点間の距離が偶数
異なる色：両頂点間の距離が奇数

以上より各頂点の色が分かれば、ある2頂点間の最短距離の偶奇が分かる。
よって、これを実装すればおｋ。
↓の実装はDFSじゃなくてBFSでやった。

abc209d_fig

LCA(Lower Common Ancestor, 最小共通祖先)を使えば各クエリ辺り $O(1)$ で2頂点間の距離を求められるので、それの偶奇を調べてもacできた。
segtree使っててコードが長いので折りたたんである。

from collections import deque

N, Q = map(int, input().split())
edge = [[] for _ in range(N)]
for _ in range(N - 1):
    x, y = map(lambda n: int(n) - 1, input().split())
    edge[x].append(y)
    edge[y].append(x)

depth_from_root = [-1] * N
queue = deque([(0, 0)])
while queue:
    now, depth = queue.popleft()
    if depth_from_root[now] != -1:
        continue
    depth_from_root[now] = depth

    for n_node in edge[now]:
        if depth_from_root[n_node] != -1:
            continue
        queue.append((n_node, depth + 1))

for _ in range(Q):
    c, d = map(lambda n: int(n) - 1, input().split())

    if abs(depth_from_root[c] - depth_from_root[d]) % 2:
        print("Road")
    else:
        print("Town")

LCA(Lowest Common Ancestor, 最小共通祖先)使った解法

LCAとは、根付き木における2頂点の共通の祖先の内で最も深い(根から最も遠い、2頂点から最も近い)頂点のこと。上の図で言えば4と5のLCAは1。
LCAが分かれば $O(1)$ で分かれば、2頂点a,b間の距離は以下の式で求まる。

(頂点aの深さ)+(頂点bの深さ)-2\times (LCAの深さ)

LCAの求め方はいくつかあるようだけど、オイラーツアーとRmQを用いて求めた。

class segtree:
    def __init__(self, n: int, identity_element_func, binary_operation_func):
        self.n = n
        self.identity = identity_element_func
        self.binary = binary_operation_func
        n2 = 1  # n2はnより大きい2の冪数
        while n2 < n:
            n2 <<= 1
        self.n2 = n2
        self.tree = [identity_element_func() for _ in range(n2 << 1)]

    def update(self, index: int, x: int):
        index += self.n2
        self.tree[index] = self.binary(self.tree[index], x)
        while index > 1:
            # (index ^ 1) はiと1の排他的論理和(XOR)
            x = self.binary(x, self.tree[index ^ 1])
            index >>= 1  # 右ビットシフトで親ノードのインデックスへ移動
            self.tree[index] = self.binary(self.tree[index], x)

    def get(self, a: int, b: int) -> int:
        result = self.identity()
        q = [(1, 0, self.n2)]
        while q:
            k, left, right = q.pop()
            if a <= left and right <= b:
                result = self.binary(result, self.tree[k])
                continue
            m = (left + right) // 2
            k <<= 1
            if a < m and left < b:
                q.append((k, left, m))
            if a < right and left < m:
                q.append((k + 1, m, right))
        return result


N, Q = map(int, input().split())
edge = [[] for _ in range(N)]
for _ in range(N - 1):
    x, y = map(lambda n: int(n) - 1, input().split())
    edge[x].append(y)
    edge[y].append(x)  # 有向グラフならこの行は消す!!
INF = 10 ** 18

height_tour = segtree(N * 2, lambda: INF, min)
first_seen_i_on_tour = [-1] * N

cnt = 0
queue = [(0, 0)]
while queue:
    now, depth = queue.pop()
    if first_seen_i_on_tour[now] != -1:
        continue
    cnt += 1
    first_seen_i_on_tour[now] = cnt
    height_tour.update(cnt, depth)
    for n_node in edge[now]:
        if first_seen_i_on_tour[n_node] != -1:
            continue
        queue.append((n_node, depth + 1))
    cnt += 1

for _ in range(Q):
    c, d = map(lambda x: int(x) - 1, input().split())
    left, right = sorted([first_seen_i_on_tour[c], first_seen_i_on_tour[d]])
    lca = height_tour.get(left, right)
    ans = (height_tour.get(left, left + 1)
           + height_tour.get(right, right + 1)
           - 2 * height_tour.get(lca, lca + 1))
    if ans % 2:
        print("Road")
    else:
        print("Town")

参考

公式解説

LCA

https://algo-logic.info/lca/

プログラミングコンテストチャレンジブック p.294

E - Shiritori

dp[i]を、自分が単語 $S_i$ を言った場合に自分が勝てるか？を表すとする。つまりdp[i]は、自分が「勝ち」、「負け」、「未定(引き分け)」の3つのいずれかを表すとする。
この時、以下の3つの遷移が考えられる。

次に言える単語 $S_j$ のdp[j]が全て負け、または言える単語が無い(頂点iを始点とする有向辺が無い)場合
自分が $S_i$ を言うと、その後の手番となる相手はどの単語を言っても自分が負ける、または言える単語が無い状態となる。
→ 相手の負け、つまりは自分の勝ちが確定する。
次に言える単語 $S_j$ のdp[j]に勝ちとなるjがある場合
自分が $S_i$ を言うと、その後の相手は自分が勝ちとなる単語を言う。
→ 相手の勝ち、つまりは自分の負けが確定する。
それ以外の場合
未定

dpを「未定(引き分け)」で初期化し、次に言える単語が無い $S_i$ のdp[i]を「勝ち」とする。
ここで「勝ち」となった頂点aへの有向辺を持つ頂点bは、上述の遷移の2つ目の場合に該当するので、「負け」となる。
「負け」となった頂点bを終点とする有向辺をもつ頂点cは、cを始点とする辺が全て「負け」となる頂点に隣接しているならばcは「勝ち」となる。
こんな感じの操作を繰り返してけばおｋ。

EDPCやってたおかげでdpは割と速く思いつけたけど後退解析の実装がうまくできなかった。

from collections import defaultdict

N = int(input())
S = [input() for _ in range(N)]

# ある単語の末尾3文字から次に遷移可能な単語のインデックス(有向辺の終点)を返す
hip_to_next_i_dict = defaultdict(list)
# ある単語の先頭3文字からその単語へ遷移してくることが可能な単語のインデックス(有向辺の始点)を返す
head_to_last_i_dict = defaultdict(list)
for i, s in enumerate(S):
    hip_to_next_i_dict[s[:3]].append(i)
    head_to_last_i_dict[s[-3:]].append(i)
"""
dp[i]は、単語siを言った場合に勝てるか？を表す
-1:未定(引き分け), 0:負け, 1:勝ち
遷移先が全て負け or 遷移先がない → 勝ち確
遷移先に勝ちがある              → 負け確
遷移先に引き分けがある          → 引き分け
これを後退解析で埋めてく
"""
dp = [-1] * N
stack = []
degree = []  # 頂点iからの出次数(iを始点とする有向辺の数)
for i, s in enumerate(S):
    degree.append(len(hip_to_next_i_dict[s[-3:]]))
    if degree[-1] == 0:
        stack.append(i)
        dp[i] = 1

while stack:
    now = stack.pop()

    for n_node in head_to_last_i_dict[S[now][:3]]:
        if dp[n_node] != -1:
            continue
        degree[n_node] -= 1

        if dp[now] == 1:
            dp[n_node] = 0
            stack.append(n_node)
        elif dp[now] == 0 and degree[n_node] == 0:
            dp[n_node] = 1
            stack.append(n_node)

for ans in dp:
    if ans == 1:
        print("Takahashi")
    elif ans == 0:
        print("Aoki")
    elif ans == -1:
        print("Draw")

AtCoder ABC209 個人的メモ

所感

A - Counting

B - Can you buy them allb

C - Not Equal

D - Collision

参考

公式解説

LCA

E - Shiritori

参考

問題の解説

後退解析

Discussion