コンピューターでは 0.1+0.2 が 0.3 ではない理由

🌼 はじめに

コンピューターでは $0.1 + 0.2$ が $0.3$ ではありません。

JavaScript

0.1 + 0.2 === 0.3 // false

JavaScript だけではなく、ほとんどのプログラミング言語は同じような結果を出力します。

今回はその理由を解説していきたいと思います。

メモリが数字を保存する方法

コンピューターがプログラムを実行するとき諸々データはメモリに保存されるので、数字もメモリに保存されます。

ですが、コンピューターの世界観では$0$と$1$しか認識できないので、10進数の数字は2進数に変換されてから保存されます。例えば、$7$は2進数に変換したら$111$なので$111$がメモリに保存されます。

小数はどう保存されるのか

では$5.75$のような小数はどうでしょうか。

ほとんどの場合は小数を保存するとき IEEE^[1] という団体が決めた標準を採用しています（IEEE 754）。この方式では小数を$1.xxxx \times 2^{e}$の形に正規化して、それを符号部・指数部・仮数部の3つの部分に分けて保存します。

実際やってみましょう。$5.75$は2進数に変換すると$101.11$になるので、これを正規化します。

$1.xxxx \times 2^{e}$の形に正規化する流れはざっくりこうです。

1. 小数点より左が $1$ になるように小数点を左もしくは右に移動
2. 小数点を移動した数字に$2^{e}$を掛ける
   • 左に$n$マス移動した場合は $e = +n$
   • 右に$n$マス移動した場合は $e = -n$

$101.11$の場合、小数点より左を$1$にするために小数点を左に2マス移動させます（$1.0111$）。小数点を左に2マス移動したので、$2^{2}$を掛けます（$1.0111 \times 2^{2}$）

正規化の例

これで正規化できたので、実際どう保存されるかを見ていきます。32ビットに保存する場合を基準として話すので、まずは32ビットのメモリ空間を確保します。

1番最初の1ビットは符号部です。ここには保存する数字が正の数だったら $0$ を、負の数だったら $1$ を入れます。$1.0111 \times 2^{2}$ は正の数なので $0$ が入ります。

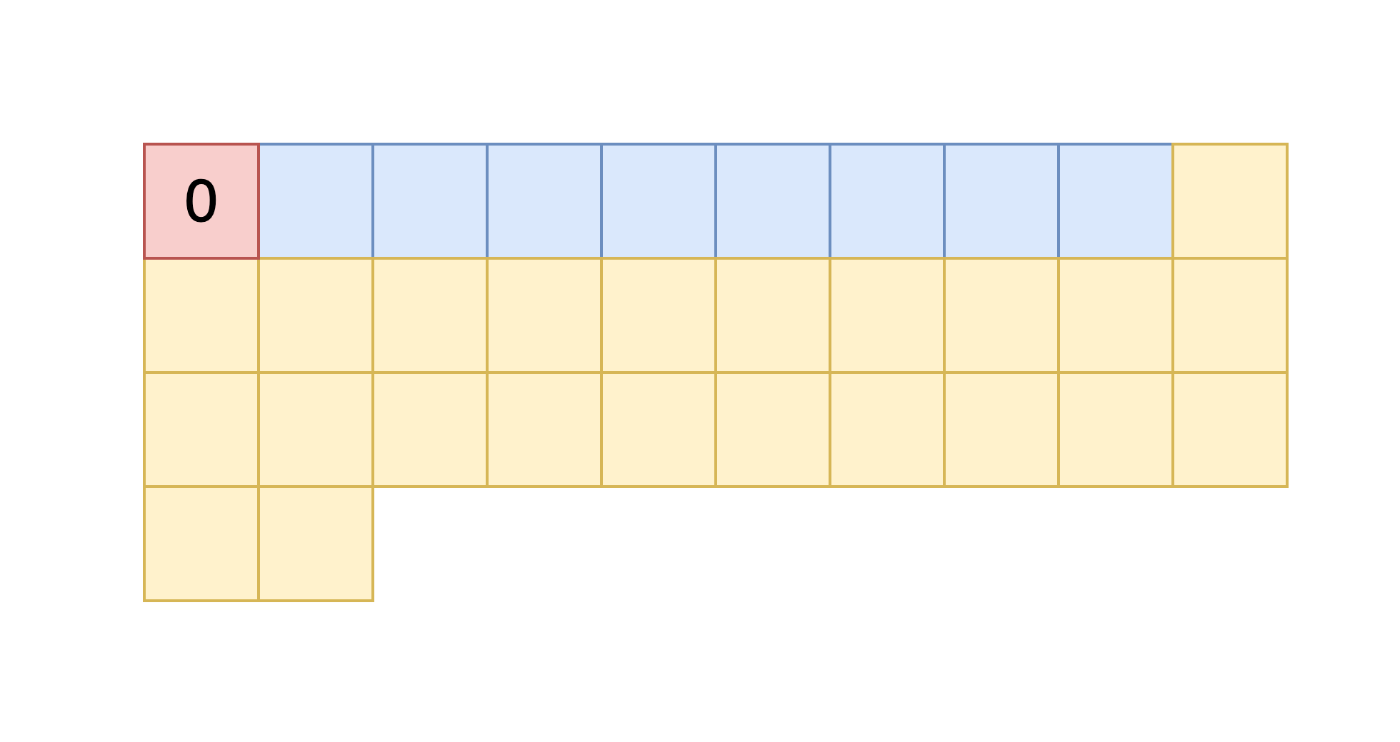
符号部

その次の8ビットは指数部です。ここには$1.xxxx \times 2^{e}$の$e$を保存します。ただそれをすぐ保存するのではなく、以下の手順で変換して保存します。

1. 指数$e$に$127$を足す
2. それを2進数に変換する

🙋‍♀️なんで127を足すんですか？

指数は正の数になることも(ex. $1.0111 \times 2^{2}$)、負の数になることも(ex. $1.01 \times 2^{-3}$)あります。指数部では指数を符号ビットなしの8ビットに保存するために$127$(バイアス)を足して、0〜255 の範囲にエンコードします。

$1.0111 \times 2^{2}$の場合$e$は$2$なので、それに$127$を足したら$129$になり、$129$を2進数に変換すると$10000001$になります。

その$10000001$が指数部に入ります。

指数部

残り23ビットは仮数部です。$1.0111 \times 2^{2}$で小数点より右の$0111$を入れます。（余った空間には$0$が入る）

仮数部

このように実数をフォーマットする方法を浮動小数点（floating point）と言います。小数点が固定ではなくて浮いてる（移動してる）から浮動と言ってるんですかね知らんけど

0.1+0.2≠0.3 になる理由

でも浮動小数点方式では正確な値を保存できない場合があります。

例えば10進数$0.1$の場合、2進数に変換すると$0.0001100110011001100110011…$のように無限小数になります。これを正規化したら$1.1001100110011001100110011… \times 2^{-4}$になり、仮数部が溢れ出ることになります。

23ビット(仮数部)に収まらない

保存容量には限界があるし無限に溢れてる数字を全部保存するわけにはいかないので、23ビットの最後のビットで1に切り上げるか、0に切り捨てることになります。^[2]

この切り上げ・切り捨てが原因で誤差が発生します。$0.1$を保存しても、仮数部が途中で切り上げられるので$0.1$そのものではなく$0.1$に近い何かの数字が保存されます。

なのでコンピューターで$0.1 + 0.2$を計算させると、実際は$0.1$に近い何かの数字と$0.2$を足しているので、ピッタリの$0.3$とは違うというのが真相です。

ふと気になって JavaScript で$0.1 + 0.2$を出力させてみたら$0.30000000000000004$になってました。

0.1 + 0.2 // 0.30000000000000004

小数を扱う時は要注意

正確な数値を扱わないといけないプロジェクトの場合、浮動小数点の誤差をちゃんと考慮しないとその誤差が原因で事故が起きることもあります。^[3]

でも浮動小数点を理解していたら、正確な数字を扱わないといけない場面が来ても色々工夫できるでしょう。

例えばお金の場合、整数に変換することで正確な値が保存できます。$12.99$ドルは100を掛けて$1299$セントに変換したら小数ではなく整数になるので誤差が発生しなくなります。

また、数字の比較のときは 0.1 + 0.2 === 0.3 のように直接比較するのではなく、誤差を比較する方法があります。

例えば$0.1 + 0.2$と$0.3$を比較する場合、２つの数字の差が許容できるほど小さいなら同じ数字だと判断する考え方です。TypeScript で簡単な関数を作成してみました。

const nearlyEqual = (a: number, b: number, eps: number = 1e-9): boolean => {
    return Math.abs(a - b) <= eps;
}

nearlyEqual(0.1 + 0.2, 0.3) // true

1e-9は$1 \times 10^{-9}$のことで、$0.000000001$という値を示します。つまり２つの数字の差が$0.000000001$以下なら同じ数字だと判断するということです。

他にはfloat(32ビット)じゃなくてdouble(64ビット)で数字を保存する方法があります。double(64ビット)だと仮数部の容量がfloat(32ビット)に比べて2倍以上増えるので、その分正確さが上がります。

double(64ビット)で保存する場合

仮数部52ビットの最後で切り上げ・切り捨てをするのでまだ正確な値ではありませんが、float(32ビット)よりもっと正確度の高い値を保存することはできます。その分メモリ容量も2倍使いますが、最近はハードウェアのスペックも良くなったのでそこまで気になる範囲ではないかもしれません。

ちなみに TypeScript ではfloatもdoubleもなく大体numberが使われていますが、numberも64ビットに保存されます。

🌷 終わり

ちょっとしたCS勉強メモでした。

地味に日本語の数学用語が難しい、正の数・負の数とか四捨五入とか初めて知った

脚注

1. IEEE(Institute of Electrical and Electronics Engineers): 電気・電子・情報分野の国際的な学会／標準化団体

2. いつ切り上げるか、もしくは切り捨てるかの基準はIEEE 754標準で決まってる

3. 湾岸戦争時$0.1$の誤差が累積されミサイルの防御が失敗し、28人が死亡。パトリオットミサイル wikipedia の「ダーランでの失敗」項目参照