重み付きUnionFindに一次関数を乗せてみた

はじめに

Atcoderで競技プログラミングを楽しんでいるluna_moonlightです。この記事では、重み付きUnionFindの上位互換として、一次関数を乗せる方法について解説していきます。

重み付きUnionFindに一次関数を乗せる方法に関して以下の記事があります。
https://qiita.com/nouka28/items/a7cf4bb7130a541e97fb
しかし、Pythonで書かれている記事は見当たらなかったので、この記事を書いていきます。

UnionFind

DisjointSetUnion(DSU)とも呼ばれます。UnionFindとは、$N$頂点の辺のないグラフに対して、以下のクエリを捌くデータ構造です。

クエリ	内容
unite(x, y)	頂点$x,y$間に無向辺を張る
is_same(x, y)	頂点$x,y$が連結か否かを返す

基本的なアイデア

森^[1]で管理する

連結か否かが重要なので、下の2つのグラフはUnionFindにおいては同一視できます。もっと言えば、閉路は無駄なので、管理するグラフは森で十分です。言いかえると、unite(x, y)を実行する際にすでに連結な頂点の間に辺を張る必要はありません。

各木を根付き木にする

各木を根付き木にすることで、根が同じか否かで連結性の判定出来ます。

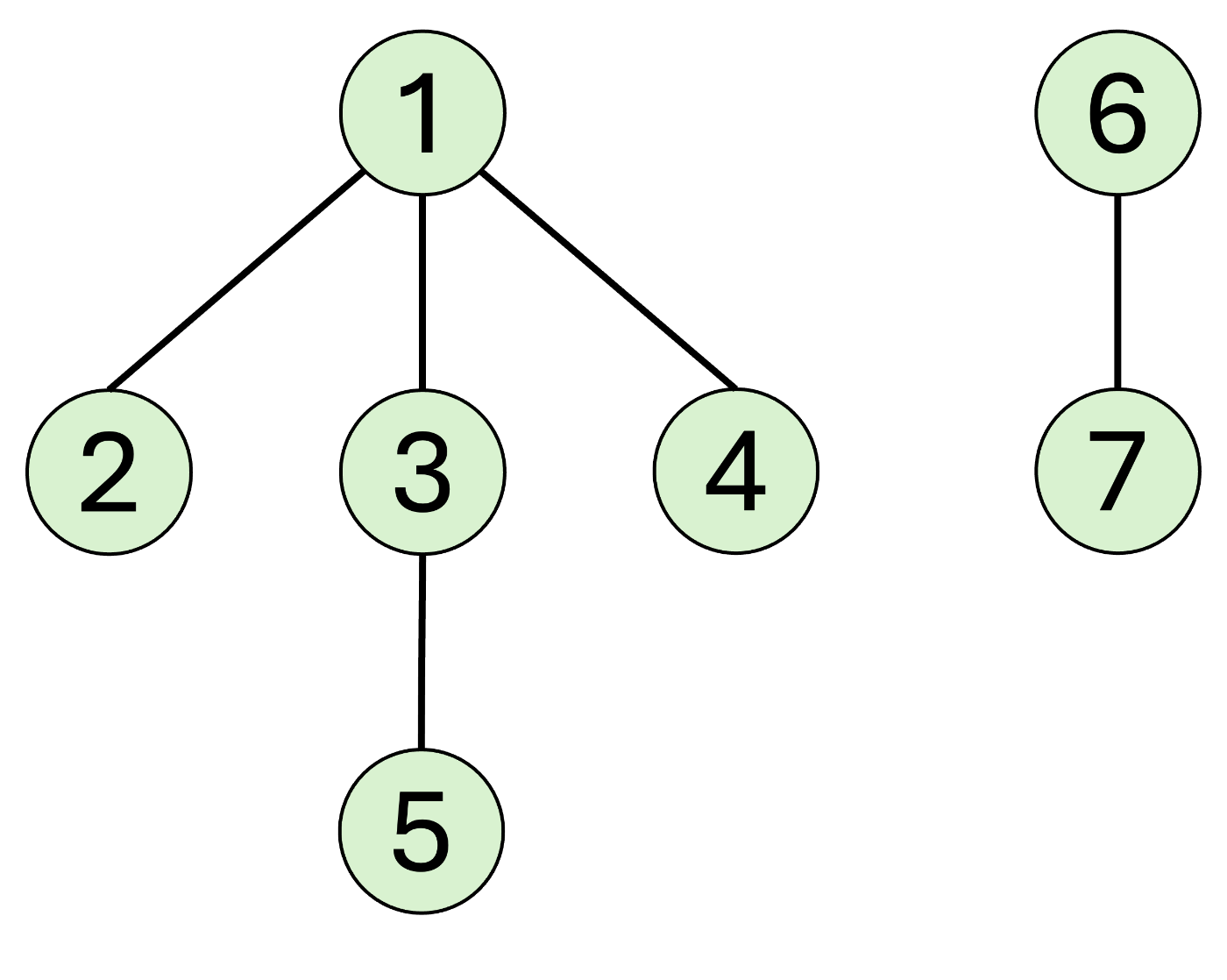
例えば、上のグラフで頂点2の根は頂点1、頂点5の根も頂点1なので連結であると言えます。頂点6の根は頂点6なので、頂点2と頂点6は連結ではないと言えます。

また、unite(x, y)を実行する際は、頂点$x$と頂点$y$の根を探し、どちらかをもう一方の子にすることで実現できます。例えば、上のグラフでunite(3, 7)を実行すると下のようなグラフになります。

実装(仮)

ここまでの内容を実装すると以下のようになります。

これだけでは、最悪のケースでとても時間がかかってしまうことに注意してください。

import sys
sys.setrecursionlimit(10 ** 7)

class UnionFind:
    def __init__(self, N):
        self.N = N
        self.parents = [-1] * N
    
    def root(self, x):
        if self.parents[x] == -1:
            return x
        return self.root(self.parents[x])
    
    def unite(self, x, y):
        rx = self.root(x)
        ry = self.root(y)
        if rx != ry:
            self.parents[rx] = ry
    
    def is_same(self, x, y):
        return self.root(x) == self.root(y)

計算量削減

下のような最悪なケースでは、木の高さが$O(N)$になり、unite(x, y)とis_same(x, y)ともに最悪計算量が$O(N)$になってしまいます。

これを解決するために、UnionFindでは以下の2つの計算量削減が提案されています。これら2つの計算量削減を行うと、計算量が$O(\alpha(N))$^[2]になることが知られています。

計算量が$O(\alpha(N))$になる証明は以下の記事をご覧ください。
https://qiita.com/kopricky/items/3e5847ab1451fe990367

マージテク

直感的に、木の高さが高い方を親にすると、unite(x, y)後の木の高さが高くならなそうです。

その直感は正しいです。unite(x, y)の際に木の高さが高い方を親にすることで、木の高さを$O(\log N)$に抑えることができます。

証明の概略

「頂点数$N$の木の深さは$\log_2 N$以下」の代わりに「深さ$d$の木の頂点数は$2^d$以上」であることを示す。
以下では、木$T$の頂点数を$|T|$とする。

帰納法を使って証明する。
(i) $d=0$のときは頂点数$1$より成立。
(ii) $d=k$のとき成り立つと仮定する。
深さ$k+1$の木$T$は、深さ$k$の木$T_1$と$T_2$をuniteして出来上がる。
帰納法の仮定から、$|T_1| \geq 2^k, |T_2| \geq 2^k$が成り立つ。
よって、出来上がる木$T$に対して、$|T| \geq 2^k + 2^k = 2^{k + 1}$が成り立つ。
すなわち、$d=k+1$のときも成り立つ。

以上(i),(ii)から、帰納法より、「深さ$d$の木の頂点数は$2^d$以上」が示せた。

経路圧縮

unite(x, y)やis_same(x, y)を実行する際に、毎回頂点$x$や頂点$y$の根を求めています。しかし、これを毎回辺をたどって求めるのは無駄が多いように思えます。そこで、一度根を求めたら、根に探索した頂点を直接張り替えてしまえばこの無駄が減ります。

例えば、左のグラフで頂点4から根を探索した場合、頂点3と頂点2を通って根に到達します。そこで、右のグラフのように、頂点2,3,4を頂点1に直接張り替えます。

実装

2つの計算量削減を導入して実装すると以下のようになります。

import sys
sys.setrecursionlimit(10 ** 7)

class UnionFind:
    def __init__(self, N):
        self.N = N
        self.parents = [-1] * N
        self.rank = [0] * N
    
    def root(self, x):
        if self.parents[x] == -1:
            return x
        self.parents[x] = self.root(self.parents[x])
        return self.parents[x]
    
    def unite(self, x, y):
        rx = self.root(x)
        ry = self.root(y)
        if rx == ry:
            return
        if self.rank[rx] < self.rank[ry]:
            rx, ry = ry, rx
        elif self.rank[rx] == self.rank[ry]:
            self.rank[rx] += 1
        self.parents[ry] = rx
    
    def is_same(self, x, y):
        return self.root(x) == self.root(y)

重み付きUnionFind

ポテンシャル付きUnionFindとも呼ばれます。重み付きUnionFindとは、長さ$N$の数列$A$に対して、以下のクエリを捌くデータ構造です。

クエリ	内容
unite(x, y, d)	$A[x]-A[y]=d$に設定する
diff(x, y)	$A[x]-A[y]$の値を返す

考え方は、普通のUnionFindとほとんど同じです。森で管理して、各辺で端点の差分を管理しています。

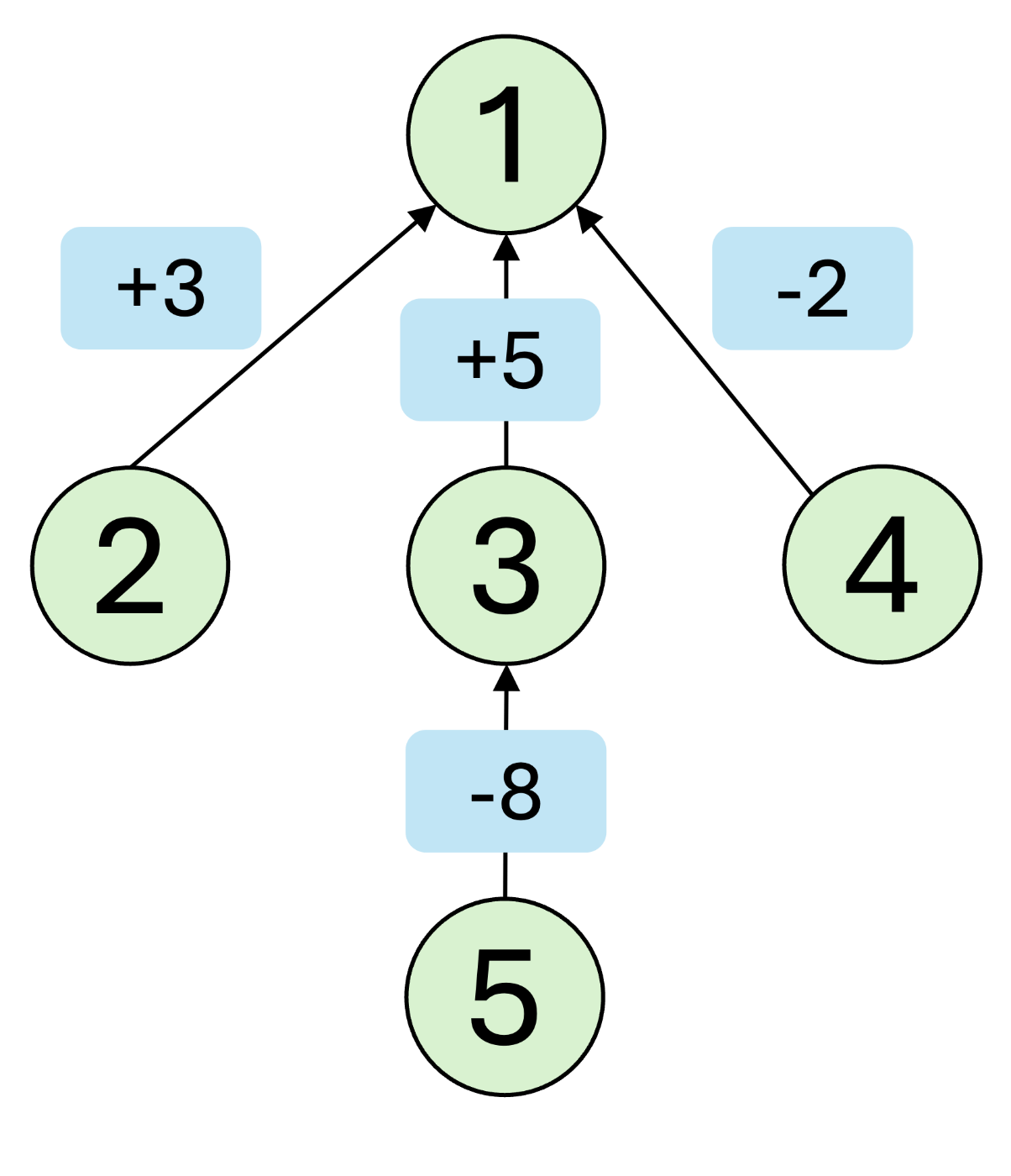
上のグラフでは、$A[1]-A[2]=3, A[1]-A[3]=5, A[1]-A[4]=-2, A[3]-A[5]=-8$を示しています。

unite(x,y,d)

unite(x,y,d)の処理を下のグラフで考えてみます。

1.rank$(x)\geq$rank$(y)$の場合

例えば、unite(5, 7, -2)というクエリが与えられたとします。普通のUnionFindと同様に頂点5の根を頂点7の根の親にするので、頂点1を頂点6の親とします。そのために、頂点1と頂点6の差分$A[1]-A[6]$を計算する必要があります。実際に、$A[1]-A[6]$を今わかっている情報から計算していきましょう。

まず、$A[1]$を$A[5]$で表します。

$$A[1] = A[3] + 5 = (A[5] - 8) + 5 = A[5] - 3$$

次に、$A[6]$を$A[7]$で表します。

$$A[6] = A[7] + 1$$

最後に、$A[1]-A[6]$を計算します。

$$A[1] - A[6] = (A[5] - 3) - (A[7] + 1) = (A[5] - A[7]) - 4 = -2 - 4 = -6$$

よって、$A[1] - A[6] = -6$なので頂点6から頂点1に重み-6の辺を張ればいいことがわかります。

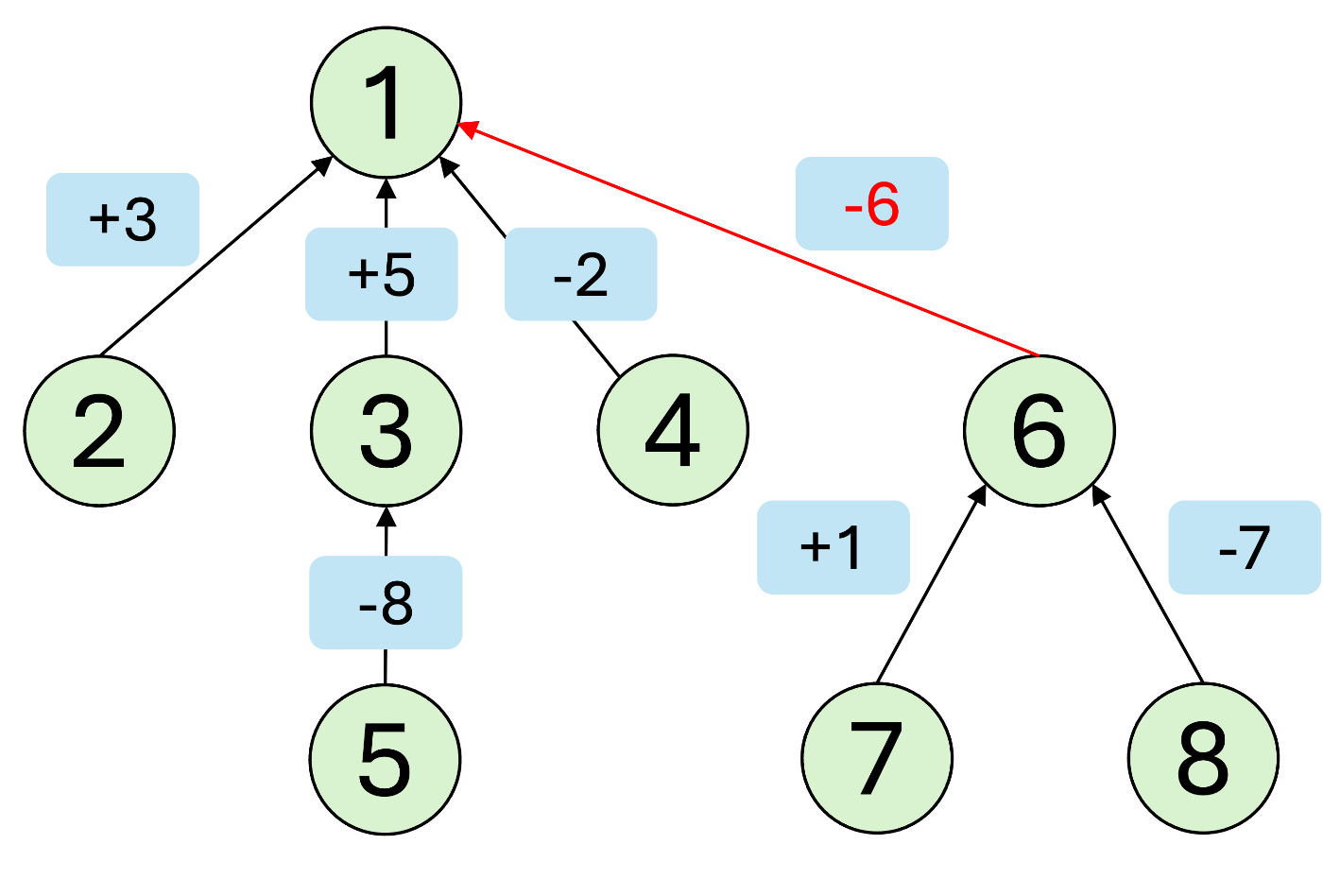
より一般的にunite(x,y,d)について考えます。
頂点$x$と頂点$y$の根をそれぞれ$r_x$と$r_y$、$\text{weight}(v)$を頂点$v$の根$r_v$と頂点$v$の差分$A[r_v]-A[v]$とします。
※$\text{weight}(v)$は頂点$v$からその根$r_v$に行くまでにたどる辺の総和で求めることができます。

すると、

$$\begin{split} A[r_x] - A[r_y] &= A[r_x] - A[x] + A[x] - (A[r_y] - A[y] + A[y])\\ &= A[x] - A[y] + \text{weight}(x) - \text{weight}(y)\\ &= d + \text{weight}(x) - \text{weight}(y) \end{split}$$

となるので、頂点$r_y$から頂点$r_x$に重み$d + \text{weight}(x) - \text{weight}(y)$の辺を張ればいいことがわかります。

2.rank$(x)\lt$rank$(y)$の場合

先ほどと同じグラフで、例えば、unite(8, 4, 2)というクエリが与えられたとします。普通のUnionFindと同様に頂点5の根を頂点7の根の親にするので、頂点1を頂点6の親とします。そのために、頂点1と頂点6の差分$A[1]-A[6]$を計算する必要があります。実際に、$A[1]-A[6]$を今わかっている情報から計算していきましょう。

まず、$A[6]$を$A[8]$で表します。

$$A[6] = A[8] - 7$$

次に、$A[1]$を$A[4]$で表します。

$$A[1] = A[4] - 2$$

最後に、$A[1]-A[6]$を計算します。

$$A[1] - A[6] = (A[4] - 2) - (A[8] - 7) = -(A[8] - A[4]) + 5 = -2 + 5 = 3$$

よって、$A[1] - A[6] = 3$なので頂点6から頂点1に重み3の辺を張ればいいことがわかります。

より一般的にunite(x,y,d)では、

$$\begin{split} A[r_y] - A[r_x] &= A[r_y] - A[y] + A[y] - (A[r_x] - A[x] + A[x])\\ &= -(A[y] - A[x]) + \text{weight}(y) - \text{weight}(x)\\ &= -d - \text{weight}(x) + \text{weight}(y) \end{split}$$

となるので、頂点$r_x$から頂点$r_y$に重み$-d - \text{weight}(x) + \text{weight}(y)$の辺を張ればいいことがわかります。

先ほどのrank$(x)\geq$rank$(y)$の場合と比べてみると、辺の張る向きと重みの符号が逆になっているだけです。rank$(x)\lt$rank$(y)$の場合に実装する際は、重みの計算をした後に符号を反転させ、$x$の根と$y$の根を交換することで、残りはrank$(x)\geq$rank$(y)$と同様の処理ができます。

$r_x=r_y$の場合、入力が矛盾してしまう可能性があります。そのときは、次に紹介するdiff(x,y)=dが成立しているか否かで判定できます。

diff(x,y)

diff(x,y)の処理を下のグラフで考えてみます。

例えば、diff(3, 8)というクエリが与えられたとします。diff(x,y)でもunite(x,y,d)と同様に、根との差分を考えます。
$A[3]-A[8]$はそれぞれの根との差分$A[0]-A[3]$と$A[0]-A[8]$を使って、

$$A[3]-A[8] = -(A[0] - A[3]) + (A[0] - A[8]) = -5 + (-6 -7) = -18$$

となるので、-18を返します。

 
より一般的にdiff(x,y)では、頂点$x$と頂点$y$の根を$r$として、

$$A[x]-A[y] = -(A[r] - A[x]) + (A[r] - A[y]) = -\text{weight}(x) + \text{weight}(y)$$

となるので、$-\text{weight}(x) + \text{weight}(y)$を返せばいいことがわかります。

頂点$x$と頂点$y$が連結でない場合、diff(x,y)の値を知ることはできません。連結か否かの判定は、普通のUnionFindのis_same(x,y)と同様に、根が同じか否かで判定できます。

実装

重み付きUnionFindを実装すると以下のようになります。

import sys
sys.setrecursionlimit(10 ** 7)

class WeightedUnionFind:
    def __init__(self, N):
        self.N = N
        self.parents = [-1] * N
        self.rank = [0] * N
        self.weight = [0] * N

    def root(self, x):
        if self.parents[x] == -1:
            return x
        rx = self.root(self.parents[x])
        self.weight[x] += self.weight[self.parents[x]]
        self.parents[x] = rx
        return self.parents[x]
    
    def get_weight(self, x):
        self.root(x)
        return self.weight[x]

    def unite(self, x, y, d):
        '''
        A[x] - A[y] = d
        '''
        w = d + self.get_weight(x) - self.get_weight(y)
        rx = self.root(x)
        ry = self.root(y)
        if rx == ry:
            _, d_xy = self.diff(x, y)
            if d_xy == d:
                return True
            else:
                return False
        if self.rank[rx] < self.rank[ry]:
            rx, ry = ry, rx
            w = -w
        if self.rank[rx] == self.rank[ry]:
            self.rank[rx] += 1
        
        self.parents[ry] = rx
        self.weight[ry] = w
        return True

    def is_same(self, x, y):
        return self.root(x) == self.root(y)
    
    def diff(self, x, y):
        if self.is_same(x, y):
            return True, self.get_weight(y) - self.get_weight(x)
        else:
            return False, 0

一次関数UnionFind

今回の本題である一次関数UnionFindとは、長さ$N$の数列$A$に対して、以下のクエリを捌くデータ構造です。

クエリ	内容
unite(x, y, a, b, c)	$aA[x]+bA[y]=c$に設定する
solve_coef(x, y)	$A[y]=pA[x]+q$を満たす頂点$p, q$を返す
get_val(x)	$A[x]$の値を返す
set_val(x, v)	$A[x]=v$と決定する

考え方は、重み付きUnionFindとほとんど同じです。差分の代わりに関数を管理しています。

上のグラフでは、$A[1]=-A[2]+5, A[1]=2A[3]+3, A[1]=3A[4]-3, A[3]=A[5]$を示しています。

unite(x,y,a,b,c)

1.頂点$x$と頂点$y$が違うグループの場合

頂点$x$と頂点$y$が違うグループの場合のunite(x,y,a,b,c)の処理を下のグラフで考えてみます。

1-1.rank$(x)\geq$rank$(y)$の場合

例えば、unite(5,7,2,3,7)というクエリが与えられたとします。普通のUnionFindと同様に頂点5の根を頂点7の根の親にするので、頂点1を頂点6の親とします。そのために、頂点1と頂点6の方程式$A[1]=pA[6]+q$を満たす$p,q$を計算する必要があります。実際に、$A[1]=pA[6]+q$を満たす$p,q$を今わかっている情報から計算していきましょう。

まず、$A[5]$を$A[1]$で表します。

$$A[1] = 2A[3] + 3 = 2(A[5] - 6) + 3 = 2A[5] - 9$$

なので、$A[5]=\dfrac{1}{2}A[1] + \dfrac{9}{2}$になります。

次に、$A[7]$を$A[6]$で表します。

$$A[6]=-3A[7]+5$$

なので、$A[7]=-\dfrac{1}{3}A[6]-\dfrac{5}{3}$になります。

最後に、$2A[5]+3A[7]=7$に代入します。

$$\begin{split} 2A[5]+3A[7]=7 &\iff 2\left(\dfrac{1}{2}A[1] + \dfrac{9}{2}\right)+3\left(-\dfrac{1}{3}A[6]-\dfrac{5}{3}\right)=7\\ &\iff A[1]-A[6]=3 \end{split}$$

よって、$A[1]=A[6]+3$なので頂点6から頂点1に$A[6]+3$の辺を張ればいいことがわかります。

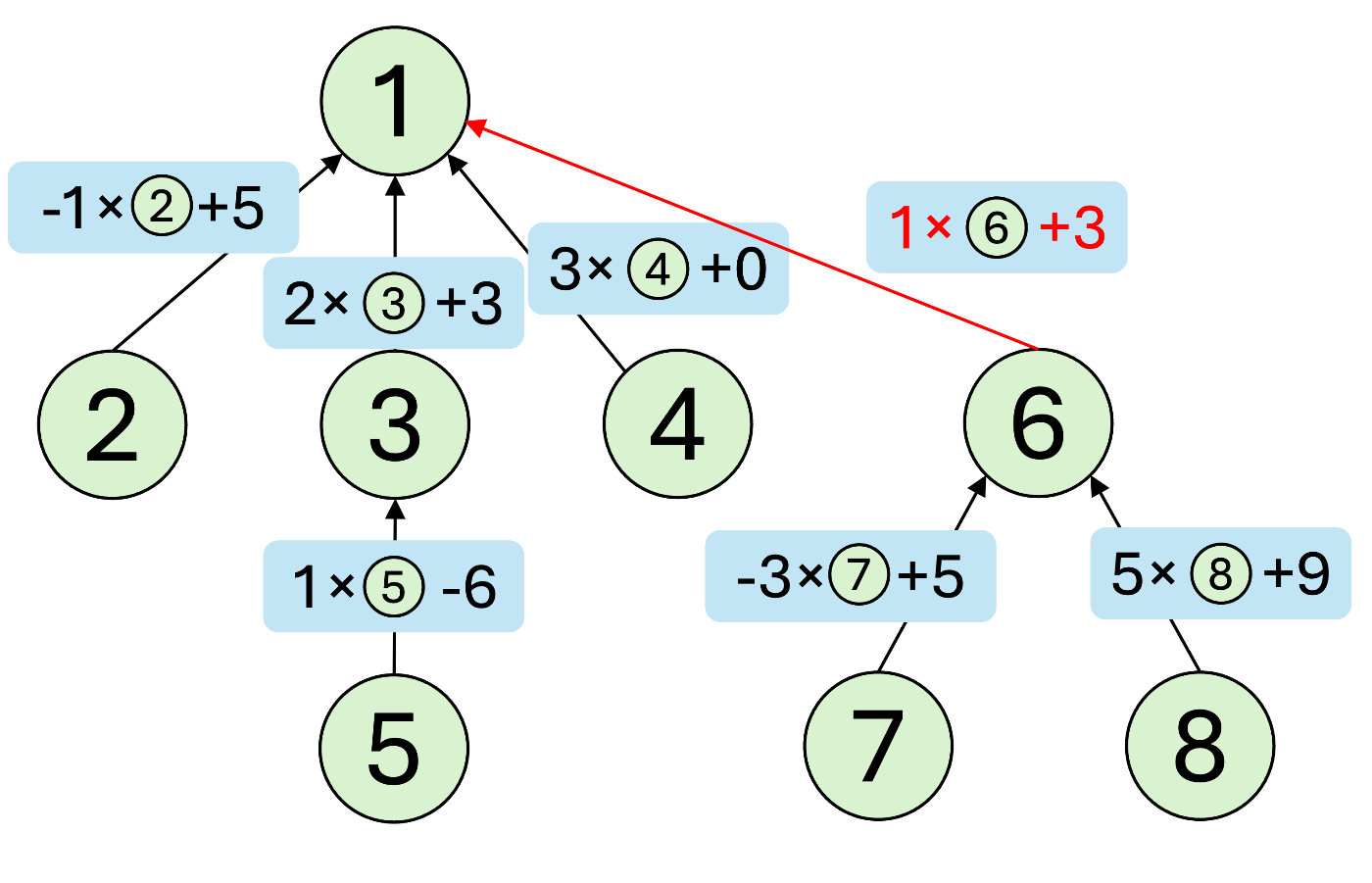
より一般的にunite(x,y,a,b,c)について考えます。
頂点$x$と頂点$y$の根をそれぞれ$r_x$と$r_y$として、$A[r_x]=p_xA[x]+q_x, A[r_y]=p_yA[y]+q_y$と表せたとします。

すると、$A[x]=\dfrac{1}{p_x}A[r_x]-\dfrac{q_x}{p_x}, A[y]=\dfrac{1}{p_y}A[r_y]-\dfrac{q_y}{p_y}$となるので、

$$\begin{split} aA[x]+bA[y]=c &\iff a\left(\dfrac{1}{p_x}A[r_x]-\dfrac{q_x}{p_x}\right)+b\left(\dfrac{1}{p_y}A[r_y]-\dfrac{q_y}{p_y}\right)=c\\ &\iff \dfrac{a}{p_x}A[r_x] + \dfrac{b}{p_y}A[r_y] = \dfrac{aq_x}{p_x} + \dfrac{bq_y}{p_y} + c \end{split}$$

よって、$A[r_x]=-\dfrac{bp_x}{ap_y}A[r_y]+\left(q_x+\dfrac{bp_xq_y}{ap_y}+\dfrac{cp_x}{a}\right)なので$頂点$r_y$から頂点$r_x$に$-\dfrac{bp_x}{ap_y}A[r_y]+\left(q_x+\dfrac{bp_xq_y}{ap_y}+\dfrac{cp_x}{a}\right)$の辺を張ればいいことがわかります。

1-2.rank$(x)\lt$rank$(y)$の場合

先ほどと同じグラフで、例えば、unite(8,2,5,1,1)というクエリが与えられたとします。普通のUnionFindと同様に頂点5の根を頂点7の根の親にするので、頂点1を頂点6の親とします。そのために、頂点1と頂点6の方程式$A[1]=pA[6]+q$を満たす$p,q$を計算する必要があります。実際に、$A[1]=pA[6]+q$を満たす$p,q$を今わかっている情報から計算していきましょう。

まず、$A[8]$を$A[6]$で表します。

$$A[6] = 5A[8] + 9$$

なので、$A[8]=\dfrac{1}{5}A[6] - \dfrac{9}{5}$になります。

次に、$A[2]$を$A[1]$で表します。

$$A[1]=-A[2]+5$$

なので、$A[2]=-A[1]+5$になります。

最後に、$5A[8]+A[2]=1$に代入します。

$$\begin{split} 5A[8]+A[2]=1 &\iff 5\left(\dfrac{1}{5}A[6] - \dfrac{9}{5}\right)+(-A[1]+5)=1\\ &\iff A[6]-A[1]=5 \end{split}$$

よって、$A[1]=A[6]-5$なので頂点6から頂点1に$A[6]-5$の辺を張ればいいことがわかります。

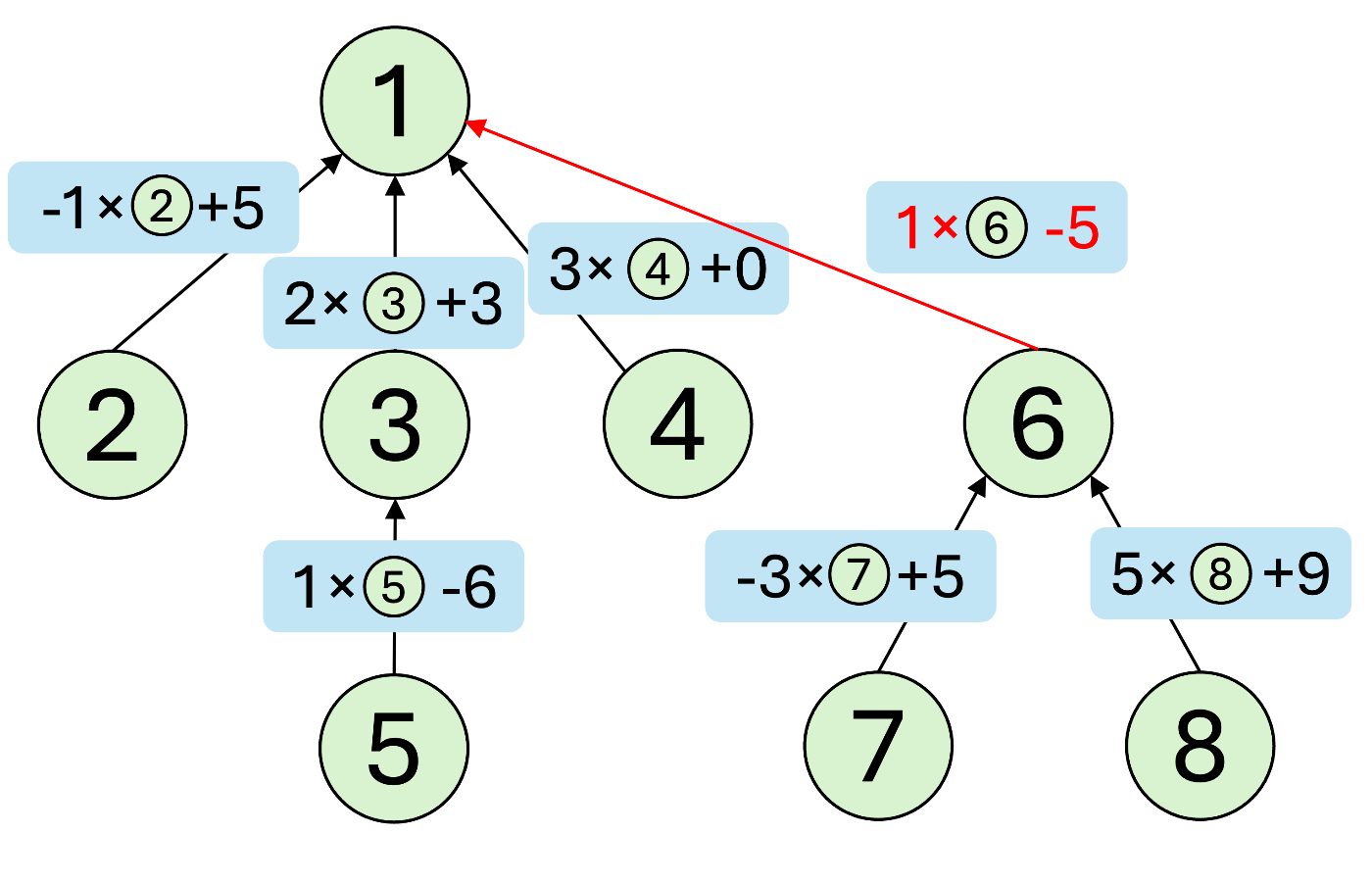
より一般的にunite(x,y,a,b,c)について考えます。
頂点$x$と頂点$y$の根をそれぞれ$r_x$と$r_y$として、$A[r_x]=p_xA[x]+q_x, A[r_y]=p_yA[y]+q_y$と表せたとします。

すると、$A[x]=\dfrac{1}{p_x}A[r_x]-\dfrac{q_x}{p_x}, A[y]=\dfrac{1}{p_y}A[r_y]-\dfrac{q_y}{p_y}$となるので、

$$\begin{split} aA[x]+bA[y]=c &\iff a\left(\dfrac{1}{p_x}A[r_x]-\dfrac{q_x}{p_x}\right)+b\left(\dfrac{1}{p_y}A[r_y]-\dfrac{q_y}{p_y}\right)=c\\ &\iff \dfrac{a}{p_x}A[r_x] + \dfrac{b}{p_y}A[r_y] = \dfrac{aq_x}{p_x} + \dfrac{bq_y}{p_y} + c \end{split}$$

よって、$A[r_y]=-\dfrac{ap_y}{bp_x}A[r_x]+\left(q_y+\dfrac{ap_yq_x}{bp_x}+\dfrac{cp_y}{b}\right)$なので頂点$r_x$から頂点$r_y$に$-\dfrac{ap_y}{bp_x}A[r_x]+\left(q_y+\dfrac{ap_yq_x}{bp_x}+\dfrac{cp_y}{b}\right)$の辺を張ればいいことがわかります。

先ほどのrank$(x)\geq$rank$(y)$の場合と比べてみると、辺の張る向きと$\{a,b\}$と$\{p_x,p_y\}$と$\{q_x,q_y\}$が逆になっているだけです。rank$(x)\lt$rank$(y)$の場合に実装する際は、これら全てを交換することで、残りはrank$(x)\geq$rank$(y)$と同様の処理ができます。

$A[x]$と$A[y]$がともに定まっている場合、入力が矛盾してしまう可能性があります。そのときは、$aA[x]+bA[y]=c$が成立しているか否かで判定できます。今回の実装では、$a\left(\dfrac{1}{p_x}A[r_x]-\dfrac{q_x}{p_x}\right)+b\left(\dfrac{1}{p_y}A[r_y]-\dfrac{q_y}{p_y}\right)=c$で判定しています。

2.頂点$x$と頂点$y$が同じグループの場合

頂点$x$と頂点$y$が同じグループのとき、$A[x]$と$A[y]$の値が一意に定まる場合があります。
頂点$x$と頂点$y$が同じグループの場合のunite(x,y,a,b,c)の処理を下のグラフで考えてみます。

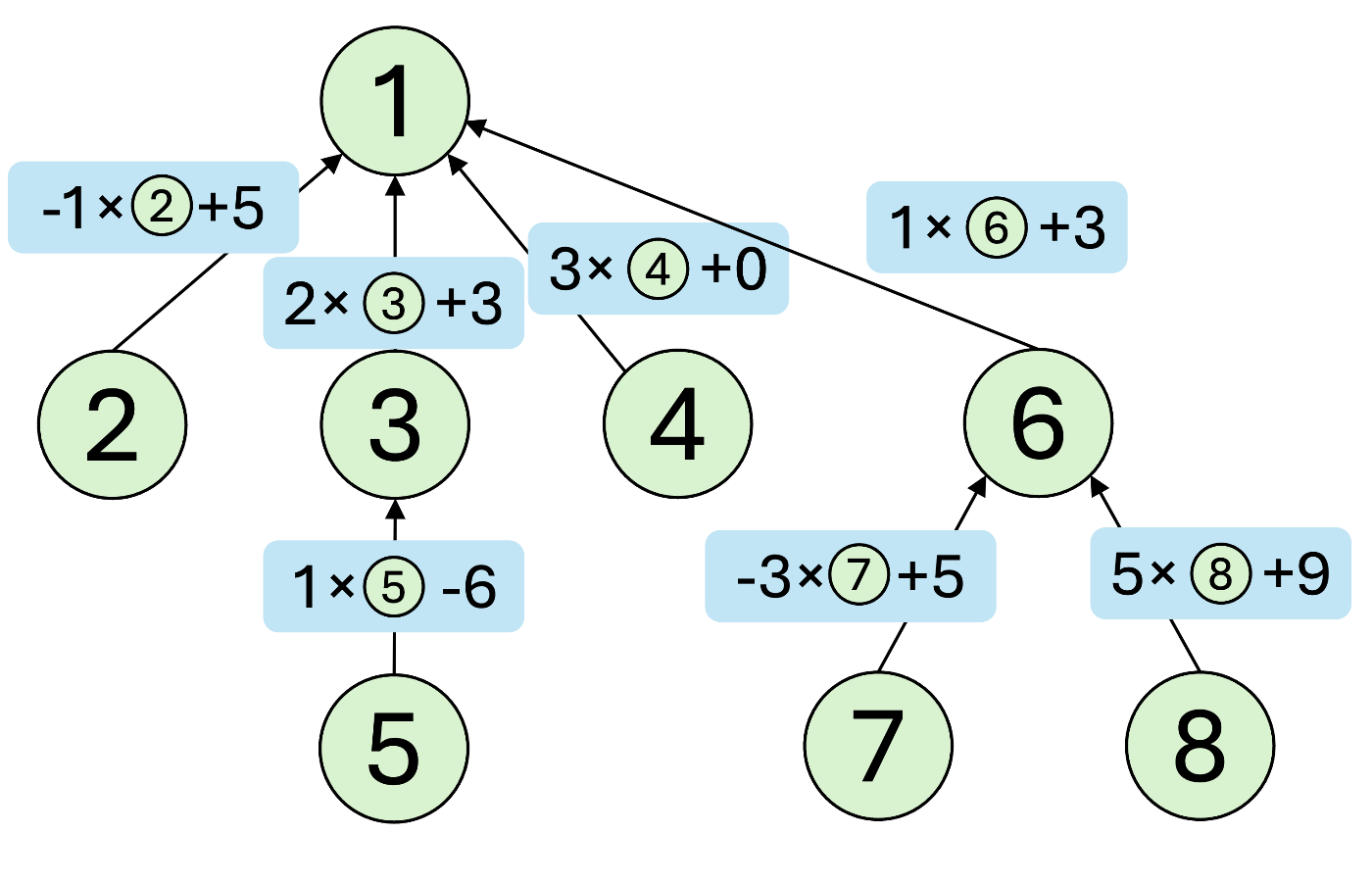
例えば、unite(5,7,4,-3,2)というクエリが与えられたとします。頂点5,7をその根である頂点1で表していきましょう。

まず、$A[5]$を$A[1]$を使って表します。

$$A[1] = 2A[3] + 3 = 2(A[5] - 6) + 3 = 2A[5] - 9$$

なので、$A[5] = \dfrac{1}{2}A[1] + \dfrac{9}{2}$になります。

次に、$A[7]$を$A[1]$を使って表します。

$$A[1] = A[6] + 3 = (-3A[7] + 5) + 3 = -3A[7] + 8$$

なので、$A[7] = \dfrac{1}{3}A[1] + \dfrac{8}{3}$になります。

最後に、$4A[8]-3[2]=2$に代入します。

$$\begin{split} 4A[5]-3A[7]=2 &\iff 4\left(\dfrac{1}{2}A[1] + \dfrac{9}{2}\right)-3\left(\dfrac{1}{3}A[1] + \dfrac{8}{3}\right)=2\\ &\iff (2A[1] + 18) - (A[1] + 8) = 2\\ &\iff A[1] = -8 \end{split}$$

よって、$A[1]=-8$に定まることがわかります。ドミノ倒しのように、他の連結成分の値もここから定まります。

 
より一般的にunite(x,y,a,b,c)について考えます。
頂点$x$と頂点$y$の根をそれぞれ$r$として、$A[r]=p_xA[x]+q_x, A[r]=p_yA[y]+q_y$と表せたとします。

すると、$A[x]=\dfrac{1}{p_x}A[r]-\dfrac{q_x}{p_x}, A[y]=\dfrac{1}{p_y}A[r]-\dfrac{q_y}{p_y}$となるので、

$$\begin{split} aA[x]+bA[y]=c &\iff a\left(\dfrac{1}{p_x}A[r]-\dfrac{q_x}{p_x}\right)+b\left(\dfrac{1}{p_y}A[r]-\dfrac{q_y}{p_y}\right)=c\\ &\iff \dfrac{a}{p_x}A[r] + \dfrac{b}{p_y}A[r] = \dfrac{aq_x}{p_x} + \dfrac{bq_y}{p_y} + c\\ &\iff \dfrac{ap_y + bp_x}{p_xp_y}A[r] = \dfrac{ap_yq_x + bp_xq_y + cp_xp_y}{p_xp_y} \end{split}$$

よって、$ap_y+bp_x \neq 0$のとき、$A[r]=\dfrac{ap_yq_x + bp_xq_y + cp_xp_y}{ap_y + bp_x}$と定まることがわかります。

$ap_y+bp_x=0$の場合、入力が矛盾してしまう可能性があります。そのときは、$ap_yq_x + bp_xq_y + cp_xp_y=0$が成立しているか否かで判定できます。

solve_coef(x,y)

solve_coef(x,y)の処理を下のグラフで考えてみます。

例えば、solve_coef(8, 2)というクエリが与えられたとします。頂点2,8をその根である頂点1で表していきましょう。

まず、$A[1]$を$A[8]$を使って表します。

$$A[1] = A[6] + 3 = (5A[8] + 9) + 3 = 5A[8] + 12$$

なので、$A[1] = 5A[8] + 12$になります。

次に、$A[1]$を$A[2]$を使って表します。

$$A[1] = -A[2] + 5$$

なので、$A[1] = -A[2] + 5$になります。

最後に、$A[1]$同士を繋ぎます。

$$5A[8] + 12 = -A[2] + 5 \iff A[2] = -5A[8] - 7$$

よって、$A[2] = -5A[8] - 7$となることがわかるので、-5,-7を返します。
 

より一般的にsolve_coef(x,y)について考えます。
頂点$x$と頂点$y$の根をそれぞれ$r$として、$A[r]=p_xA[x]+q_x, A[r]=p_yA[y]+q_y$と表せたとします。

$A[r]$同士を繋ぐと、

$$p_xA[x]+q_x = p_yA[y]+q_y \iff A[y] = \dfrac{p_x}{p_y}A[x] + \dfrac{q_x - q_y}{p_y}$$

$A[y] = \dfrac{p_x}{p_y}A[x] + \dfrac{q_x - q_y}{p_y}$となることがわかるので、$\dfrac{p_x}{p_y},\dfrac{q_x - q_y}{p_y}$を返します。

頂点$x$と頂点$y$が連結でない場合、solve_coef(x,y)の値を知ることはできません。連結か否かの判定は、普通のUnionFindのis_same(x,y)と同様に、根が同じか否かで判定できます。

get_val(x)とset_val(x, v)

get_val(x)とset_val(x, v)については、$A[x]$が一意に定まっている場合、その値を取得、設定する入力に矛盾がないか判定することができます。$A[x]$が一意に定まっていない場合、その値を取得できませんが、矛盾の判定なしに設定することができます。

今回の実装では、頂点$x$の根$r_x$に対して、$A[r_x]$から情報を復元する方法を使っています。$A[r_x]$が一意に定まっていて、$A[r_x]=p_xA[x]+q_x$と表せたとすると、
get_val(x)では、$A[x]=\dfrac{1}{p_x}A[r_x] - \dfrac{q_x}{p_x}$で復元できます。
set_val(x,v)では、$A[r_x]=p_xA[x]+q_x$が成立しているか否かで入力が矛盾しているか判定できます。

実装

一次関数UnionFindを実装すると以下のようになります。

from fractions import Fraction
import sys
sys.setrecursionlimit(10 ** 7)

class UnionFindLinear:
    def __init__(self, N):
        self.N = N
        self.parents = [-1] * N
        self.rank = [0] * N
        self.coef_p = [1] * N
        self.coef_q = [0] * N
        self.value = [0] * N
        self.specify = [False] * N

    def root(self, x):
        if self.parents[x] == -1:
            return x
        px = self.root(self.parents[x])
        self.coef_p[x] = self.coef_p[self.parents[x]] * self.coef_p[x]
        self.coef_q[x] = self.coef_p[self.parents[x]] * self.coef_q[x] + self.coef_q[self.parents[x]]
        self.parents[x] = px
        return self.parents[x]

    def get_coef(self, x):
        self.root(x)
        return self.coef_p[x], self.coef_q[x]

    def unite(self, x, y, a, b, c):
        '''
        aA[x] + bA[y] = c
        '''
        if a == 0 or b == 0:
            return False
        
        rx = self.root(x)
        px, qx = self.get_coef(x)
        ry = self.root(y)
        py, qy = self.get_coef(y)
    
        if self.specify[rx] and self.specify[ry]:
            return a * Fraction(self.value[rx] - qx, px) + b * Fraction(self.value[ry] - qy, py) == c
    
        if rx == ry:
            ca = a * px + b * py
            cb = a * py * qx + b * px * qy + c * px * py
            if ca == 0:
                return cb == 0
            self.specify[rx] = True
            self.value[rx] = Fraction(cb, ca)
            return True
    
        if self.rank[rx] < self.rank[ry]:
            rx, ry = ry, rx
            a, b = b, a
            px, py = py, px
            qx, qy = qy, qx
        if self.rank[rx] == self.rank[ry]:
            self.rank[rx] += 1

        self.parents[ry] = rx
        self.coef_p[ry] = Fraction(-b * px, a * py)
        self.coef_q[ry] = qx + Fraction(b * px * qy, a * py) + Fraction(c * px, a)
        if self.specify[ry]:
            self.specify[rx] = True
            self.value[rx] = self.coef_p[ry] * self.value[ry] + self.coef_q[ry]
        return True

    def is_same(self, x, y):
        return self.root(x) == self.root(y)

    def solve_coef(self, x, y):
        if not self.is_same(x, y):
            return False, 0, 0
        else:
            px, qx = self.get_coef(x)
            py, qy = self.get_coef(y)
            return True, Fraction(px, py), Fraction(qx - qy, py)

    def get_val(self, x):
        rx = self.root(x)
        px, qx = self.get_coef(x)
        if not self.specify[rx]:
            return False, 0
        else:
            return True, Fraction(self.value[rx] - qx, px)

    def set_val(self, x, v):
        rx = self.root(x)
        px, qx = self.get_coef(x)
        if self.specify[rx]:
            return px * v + qx == self.value[rx]
        self.specify[rx] = True
        self.val[rx] = px * v + qx
        return True

使用例

1. ABC328 F - Good Set Query

解答例

N, Q = map(int, input().split())
uf = UnionFindLinear(N)
S = []
for i in range(Q):
    a, b, d = map(int, input().split())
    a -= 1
    b -= 1
    if uf.unite(a, b, 1, -1, d):
        S.append(i + 1)

print(*S)

2. 競プロ典型90問 068 - Paired Information

解答例

N = int(input())
Q = int(input())
uf = UnionFindLinear(N)
for _ in range(Q):
    T, X, Y, V = map(int, input().split())
    X -= 1
    Y -= 1
    if T == 0:
        uf.unite(X, Y, 1, 1, V)
    elif T == 1:
        f, p, q = uf.solve_coef(X, Y)
        if f:
            print(p * V + q)
        else:
            print('Ambiguous')

まとめ

この記事では、重み付きUnionFindに一次関数を乗せる方法について解説しました。実は、重み付きUnionFindは一次関数に限らず、群^[3]が乗るそうです。この記事では、そこまでの抽象化はできなかったため、重み付きUnionFindに群を乗せる方法について模索したいと思います。

脚注

1. 閉路を持たないグラフ。

2. $\alpha(x)$は、アッカーマン関数の逆関数。単調増加だが、とてつもなく増加速度が遅いため、実質的に$O(1)$とみなせる。

3. 1.結合法則、2.単位元の存在、3.逆元の存在を満たす集合と二項演算の組。具体的には、整数の集合$\mathbb{Z}$と通常の加算$+$の組$(\mathbb{Z},+)$や一次関数の集合$G$と通常の関数の合成$\circ$の組$(G,\circ)$など。