量子コンピュータでALUを作ってみた(量子回路編)

はじめに

オンライン公開伴走型量子コンピューティング講座QC4U2卒業生のluna_moonlightです。この記事では実装については行わず、古典回路におけるALUの作り方と量子回路への変換について解説していきます。実装については、次の記事で解説していきます。

量子コンピュータで加算回路を実装するという記事はいくつか見つかりますが、ALUの実装まで行っている記事は見当たらなかったので、この記事を書いていきます。

準備

量子コンピュータでALUを実装する前に、必要な論理ゲートなどの量子ゲート表現について解説していきます。

ANDゲート

ANDゲートは、CCX(Toffoli)ゲートを使って下のように表せます。CCXゲートは2つのコントロールビットがともに$1$のとき、ターゲットビットを$0, 1$反転します。

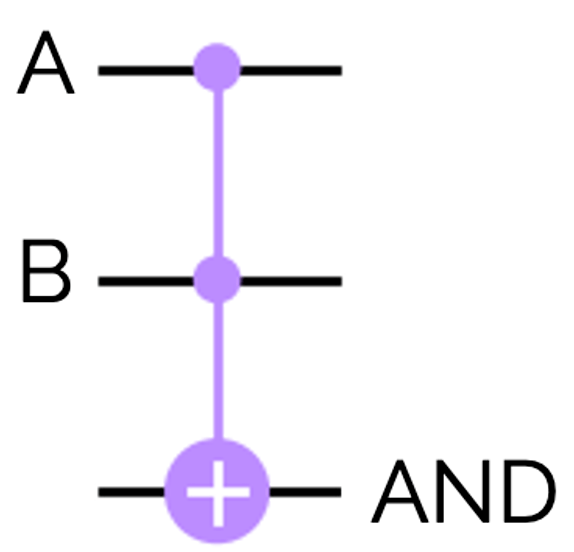
$AND_{in}$が常に$0$であることに注意して計算すると下のようになり、確かにANDゲートの結果と一致しています。

行列計算

$A=0$, $B=0$のとき

$$CCX\ket{000}= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{000}$$

$A=0$, $B=1$のとき

$$CCX\ket{010}= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{010}$$

$A=1$, $B=0$のとき

$$CCX\ket{100}= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{100}$$

$A=1$, $B=1$のとき

$$CCX\ket{110}= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ \end{pmatrix} =\ket{111}$$

$A_{in}$	$B_{in}$	$AND_{in}$	$A_{out}$	$B_{out}$	$AND_{out}$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$0$
$1$	$0$	$0$	$1$	$0$	$0$
$1$	$1$	$0$	$1$	$1$	$1$

XORゲート

次にXORゲートは、CXゲートを使って下のように表せます。CXゲートはコントロールビットが$1$のとき、ターゲットビットを$0, 1$反転します。

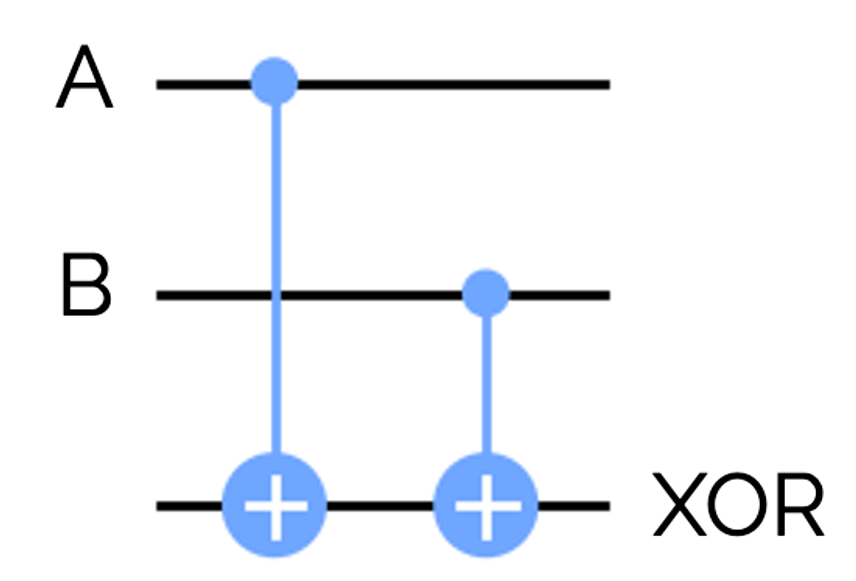
$XOR_{in}$が常に$0$であることに注意して計算すると下のようになり、確かにXORゲートの結果と一致しています。

行列計算

$A=0$, $B=0$のとき

$$\begin{split} CX_{1,2}CX_{0,2}\ket{000}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{000} \end{split}$$

$A=0$, $B=1$のとき

$$\begin{split} CX_{1,2}CX_{0,2}\ket{010}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{011} \end{split}$$

$A=1$, $B=0$のとき

$$\begin{split} CX_{1,2}CX_{0,2}\ket{100}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{pmatrix} =\ket{101} \end{split}$$

$A=1$, $B=1$のとき

$$\begin{split} CX_{1,2}CX_{0,2}\ket{110}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{pmatrix} =\ket{110} \end{split}$$

$A_{in}$	$B_{in}$	$XOR_{in}$	$A_{out}$	$B_{out}$	$XOR_{out}$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$1$	$0$	$1$	$1$	$0$

ORゲート

ORゲートは、CXゲートとCCXゲートを使って下のように表せます。

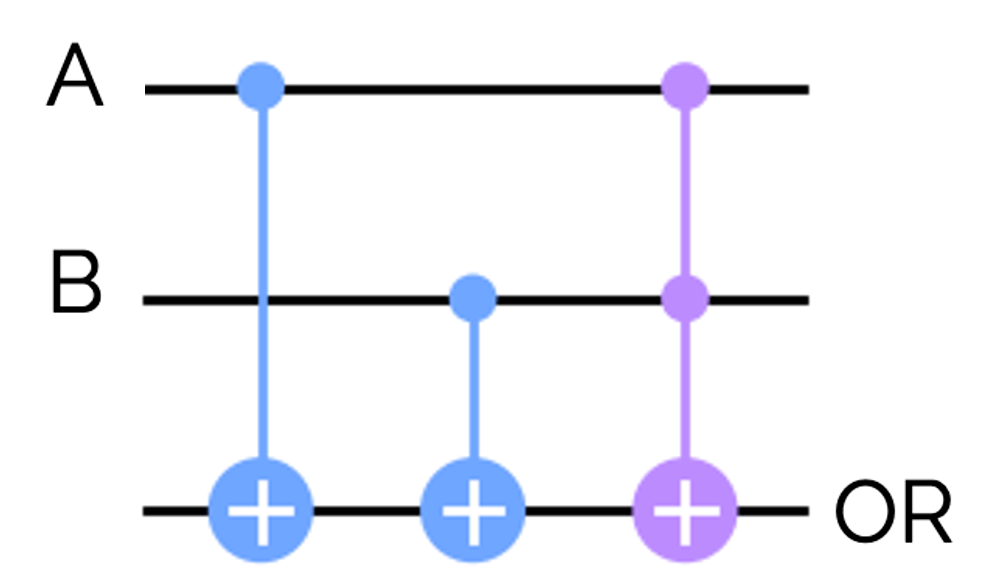
$OR_{in}$が常に$0$であることに注意して計算すると下のようになり、確かにORゲートの結果と一致しています。

行列計算

$A=0$, $B=0$のとき

$$\begin{split} CCX\,CX_{1,2}CX_{0,2}\ket{000}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{000} \end{split}$$

$A=0$, $B=1$のとき

$$\begin{split} CCX\,CX_{1,2}CX_{0,2}\ket{010}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ \end{pmatrix} =\ket{011} \end{split}$$

$A=1$, $B=0$のとき

$$\begin{split} CCX\,CX_{1,2}CX_{0,2}\ket{100}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{pmatrix}\\ &= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{pmatrix} =\ket{101} \end{split}$$

$A=1$, $B=1$のとき

$$\begin{split} CCX\,CX_{1,2}CX_{0,2}\ket{110}&= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{pmatrix}\\ &=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ \end{pmatrix}\\ &= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ \end{pmatrix} =\ket{111} \end{split}$$

$A_{in}$	$B_{in}$	$OR_{in}$	$A_{out}$	$B_{out}$	$OR_{out}$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$1$	$0$	$1$	$1$	$1$

マルチプレクサ

マルチプレクサとは、選択制御入力$S$に応じて、入力$D_0, D_1$から一方を出力する回路です。真理値表で書くと下の表のようになります。

$D_0$	$D_1$	$S$	$X$
$0$	$0$	$0$	$0$
$0$	$0$	$1$	$0$
$0$	$1$	$0$	$0$
$0$	$1$	$1$	$1$
$1$	$0$	$0$	$1$
$1$	$0$	$1$	$0$
$1$	$1$	$0$	$1$
$1$	$1$	$1$	$1$

古典版

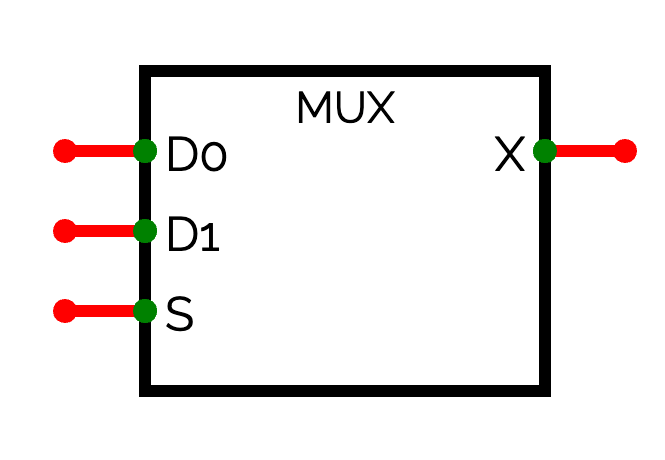
古典的な論理ゲートで表現すると下のようになります。

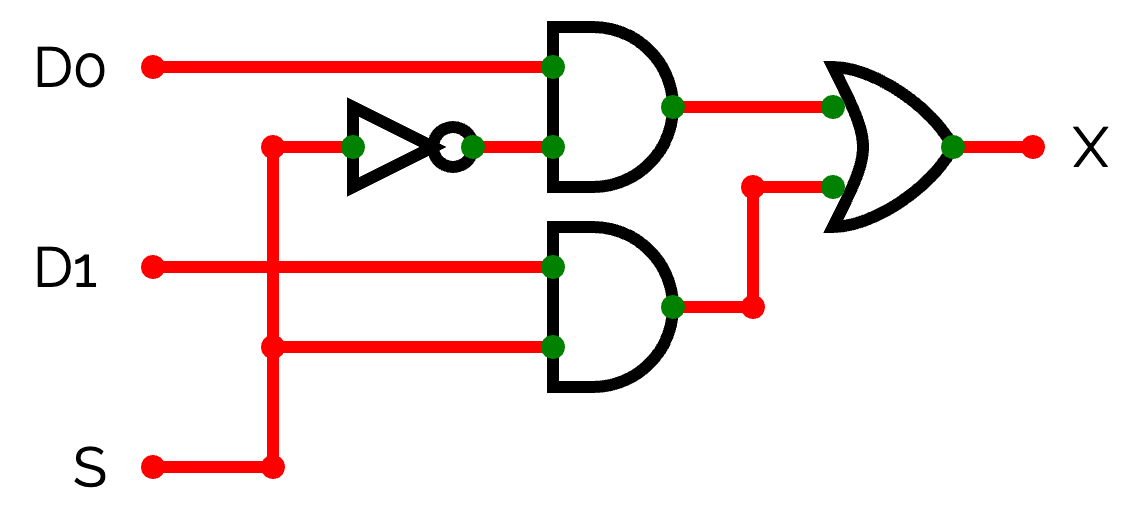
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

量子ゲート版

それでは、先ほど紹介したマルチプレクサを量子ゲートに置き換えていきましょう。ORゲート、ANDゲート、NOT(X)ゲートを使って全加算器を表現すると、下のようになります。

量子複製不可能定理により、$\ket{0}$から$\ket{S}$を複製できないため、$\ket{S}$に直接Xゲートを適用して$D_0 \cdot \overline{S}$を計算しています。その後、もう一度Xゲートを適用することで元の$\ket{S}$に戻しています。

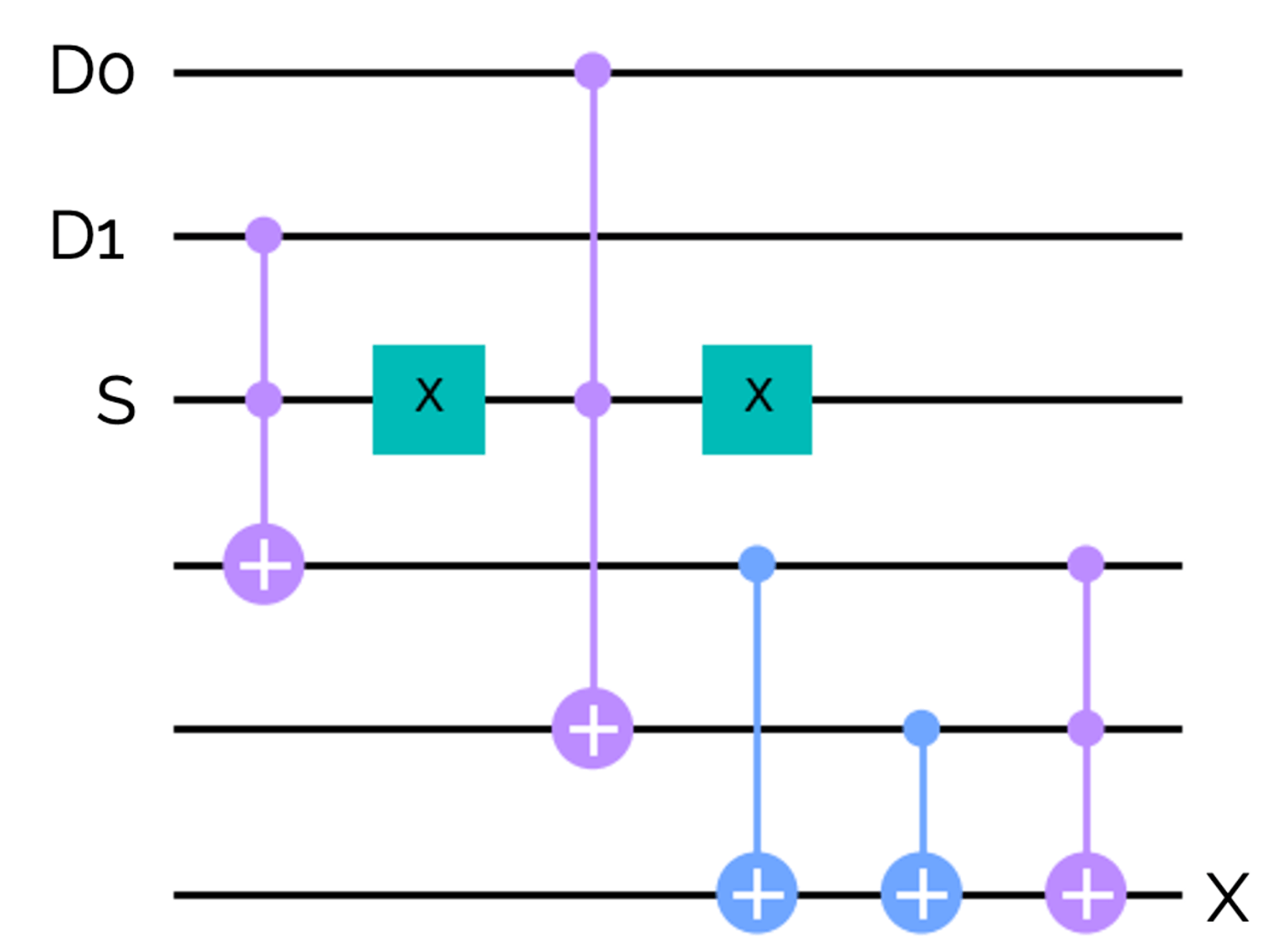
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

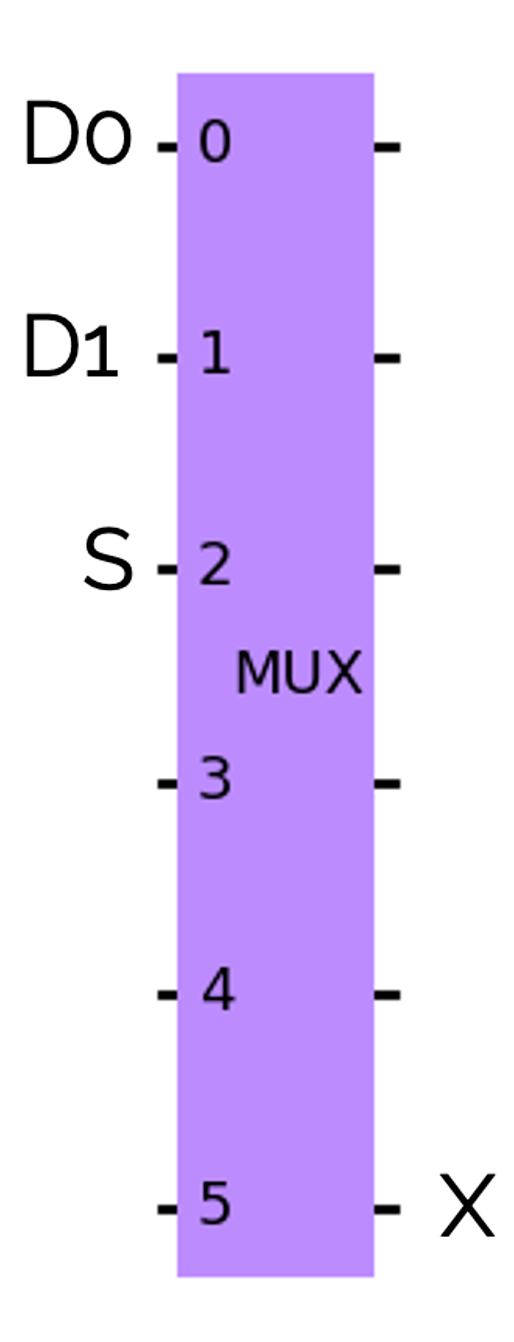
半加算器

古典版

半加算器とは、1桁の2進数を2つ足し合わせた結果を返す回路です。真理値表で書くと下の表のようになります。$A$と$B$は入力ビット、$S$は和の1桁目、$C_{out}$は和の2桁目(繰り上がり)を表しています。

$A$	$B$	$C_{out}$	$S$	対応関係
$0$	$0$	$0$	$0$	$0_{(2)} + 0_{(2)} = 00_{(2)}$
$0$	$1$	$0$	$1$	$0_{(2)} + 1_{(2)} = 01_{(2)}$
$1$	$0$	$0$	$1$	$1_{(2)} + 0_{(2)} = 01_{(2)}$
$1$	$1$	$1$	$0$	$1_{(2)} + 1_{(2)} = 10_{(2)}$

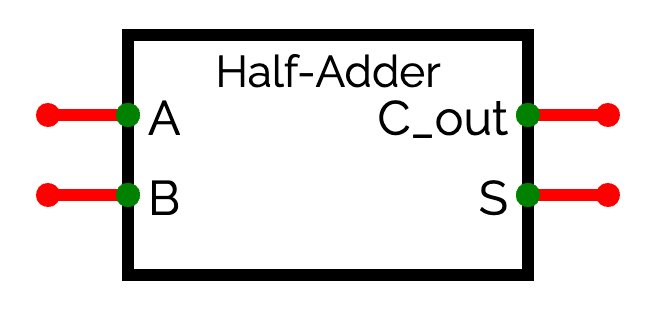
真理値表をみると$C_{out}$は$A$と$B$のANDに、$S$は$A$と$B$のXORに対応していることがわかります。なので、回路図で描くと下のようになります。

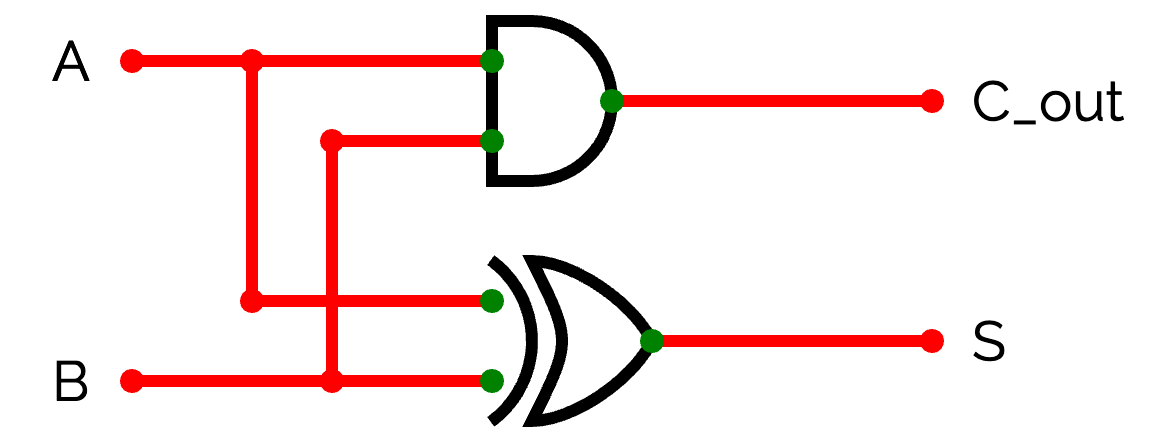
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

量子ゲート版

それでは、先ほど紹介した半加算器を量子ゲートに置き換えていきましょう。ANDゲートとXORゲートを使って半加算器を表現すると、下のようになります。

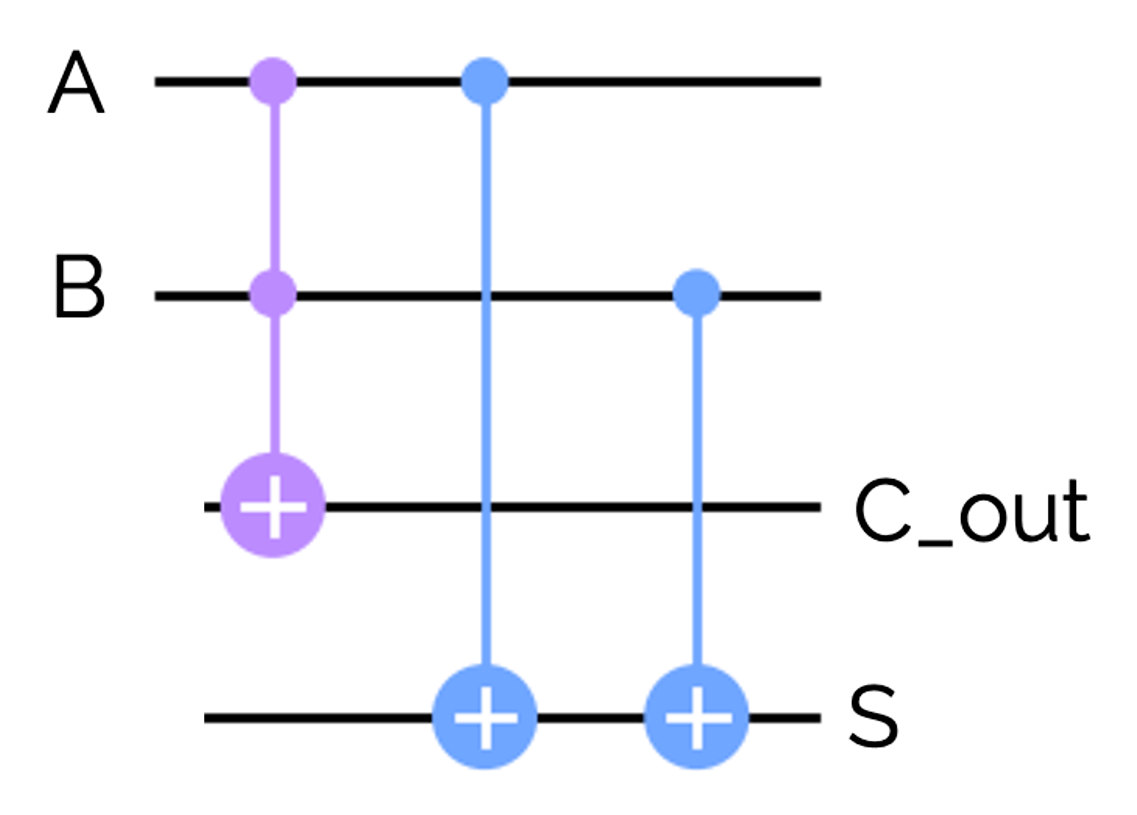
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

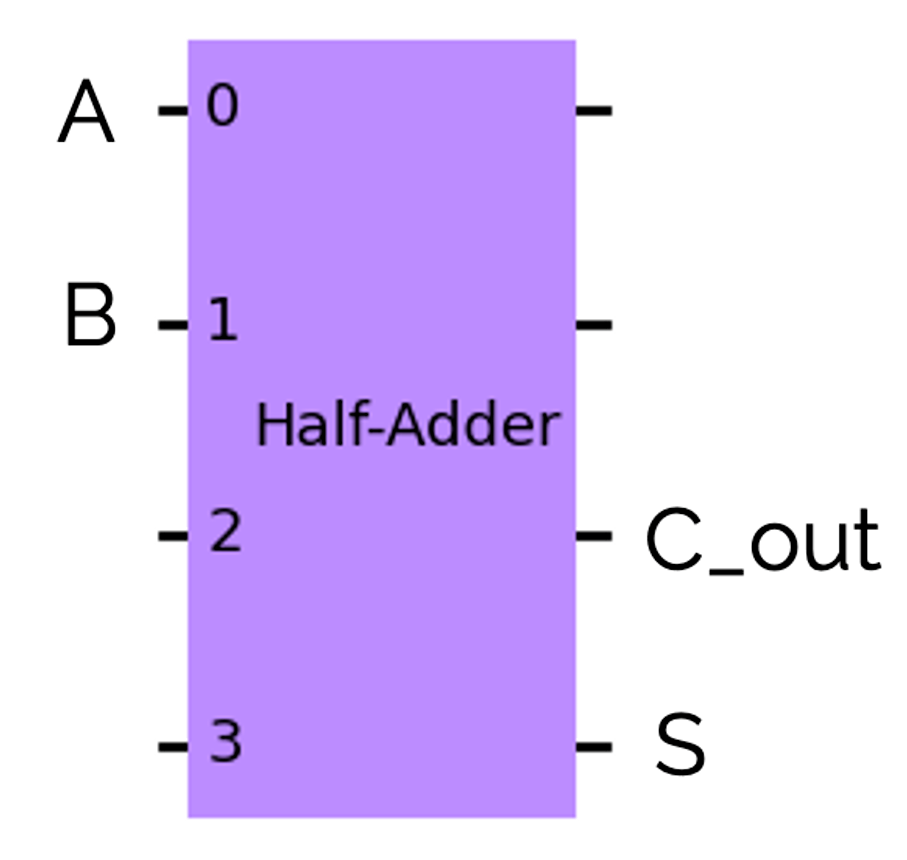
全加算器

古典版

複数ビットの加算を行うときには、前のビットから繰り上がりが発生する可能性があります。そのような場合にも対応できるように、全加算器と呼ばれる1桁の2進数を3つ足し合わせた結果を返す回路を作成します。真理値表で書くと下の表のようになります。$A$と$B$は入力ビット、$C_{in}$は繰り上がり入力、$S$は和の1桁目、$C_{out}$は和の2桁目(繰り上がり)を表しています。

$A$	$B$	$C_{in}$	$C_{out}$	$S$	対応関係
$0$	$0$	$0$	$0$	$0$	$0_{(2)} + 0_{(2)} + 0_{(2)} = 00_{(2)}$
$0$	$0$	$1$	$0$	$1$	$0_{(2)} + 0_{(2)} + 1_{(2)} = 01_{(2)}$
$0$	$1$	$0$	$0$	$1$	$0_{(2)} + 1_{(2)} + 0_{(2)} = 01_{(2)}$
$0$	$1$	$1$	$1$	$0$	$0_{(2)} + 1_{(2)} + 1_{(2)} = 10_{(2)}$
$1$	$0$	$0$	$0$	$1$	$1_{(2)} + 0_{(2)} + 0_{(2)} = 01_{(2)}$
$1$	$0$	$1$	$1$	$0$	$1_{(2)} + 0_{(2)} + 1_{(2)} = 10_{(2)}$
$1$	$1$	$0$	$1$	$0$	$1_{(2)} + 1_{(2)} + 0_{(2)} = 10_{(2)}$
$1$	$1$	$1$	$1$	$1$	$1_{(2)} + 1_{(2)} + 1_{(2)} = 11_{(2)}$

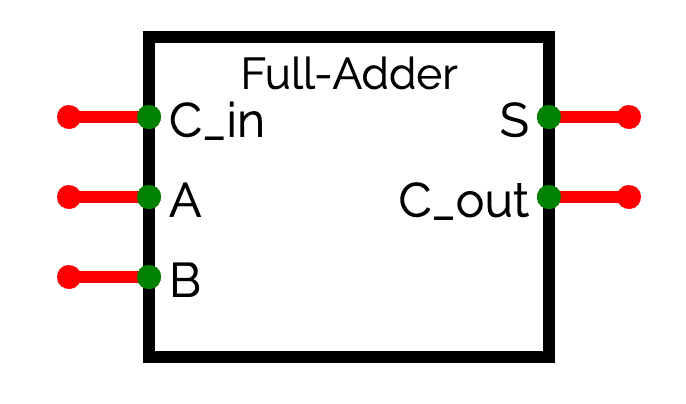
結論から言ってしまうと、先ほど作った半加算器とORゲートを使って下のような回路になります。$A, B, C_{in}$に$0, 1$を代入して回路を辿ると確かに上の真理値表と一致することがわかります。

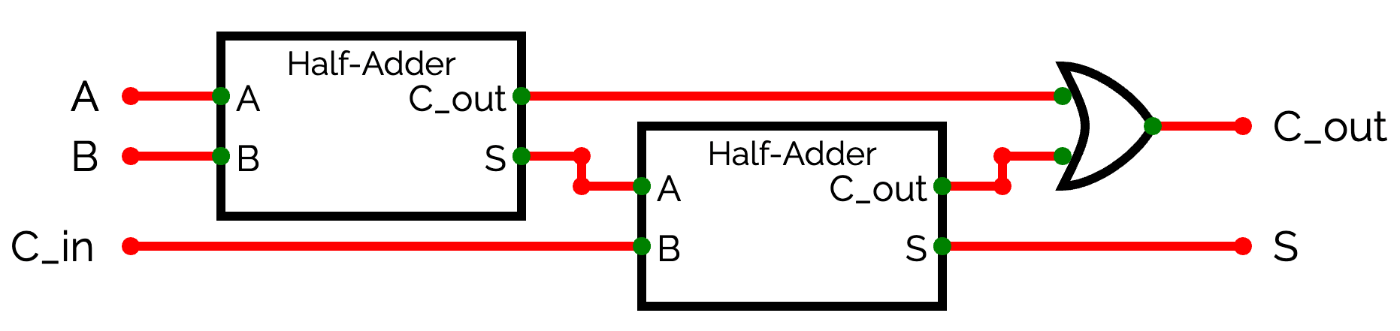
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

入力や出力の順番が上の回路とは異なっていることに注意してください。

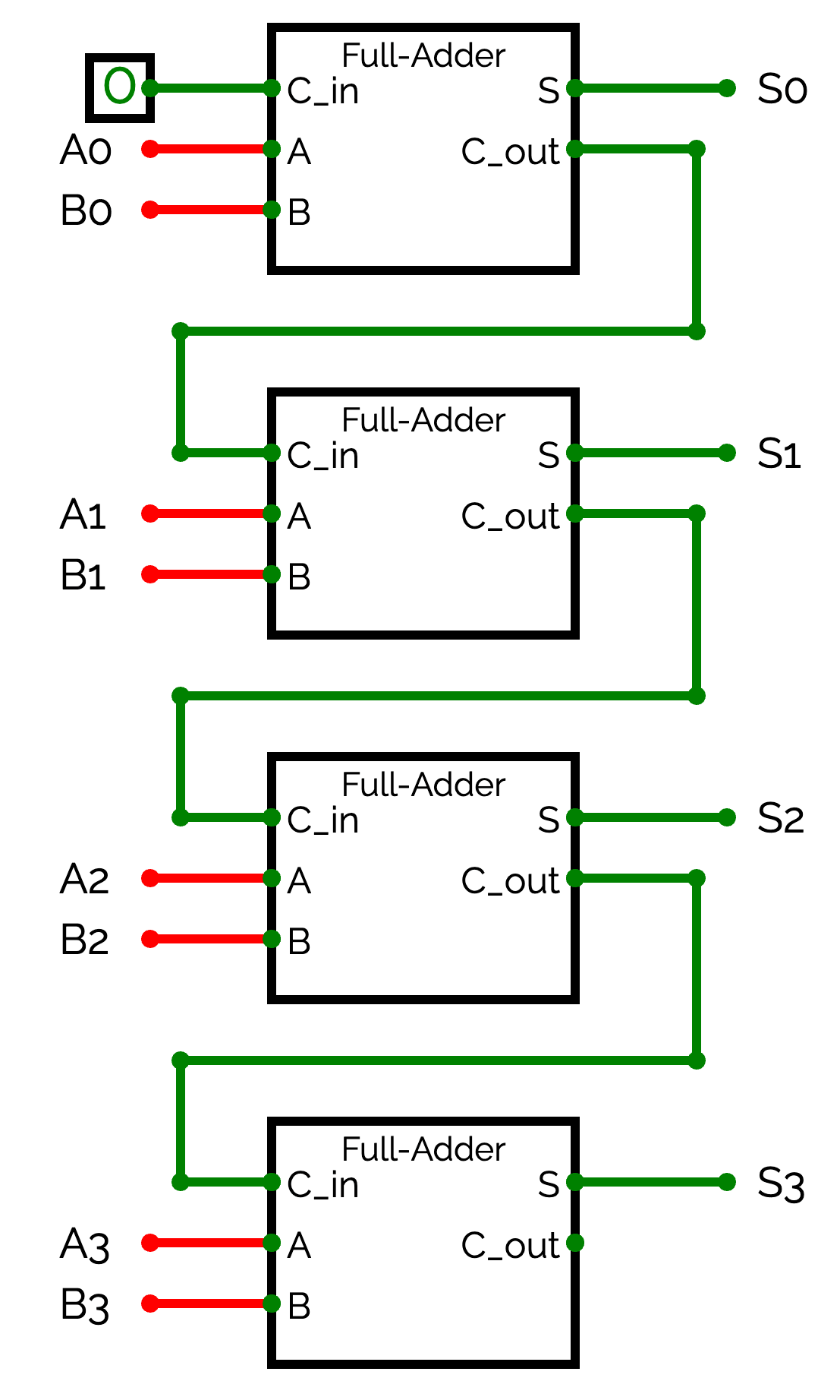
全加算器をつなげることで、複数ビットの計算にも対応できるようになります。例えば4ビット同士の加算は4つの全加算器を用いて下のような回路になります。

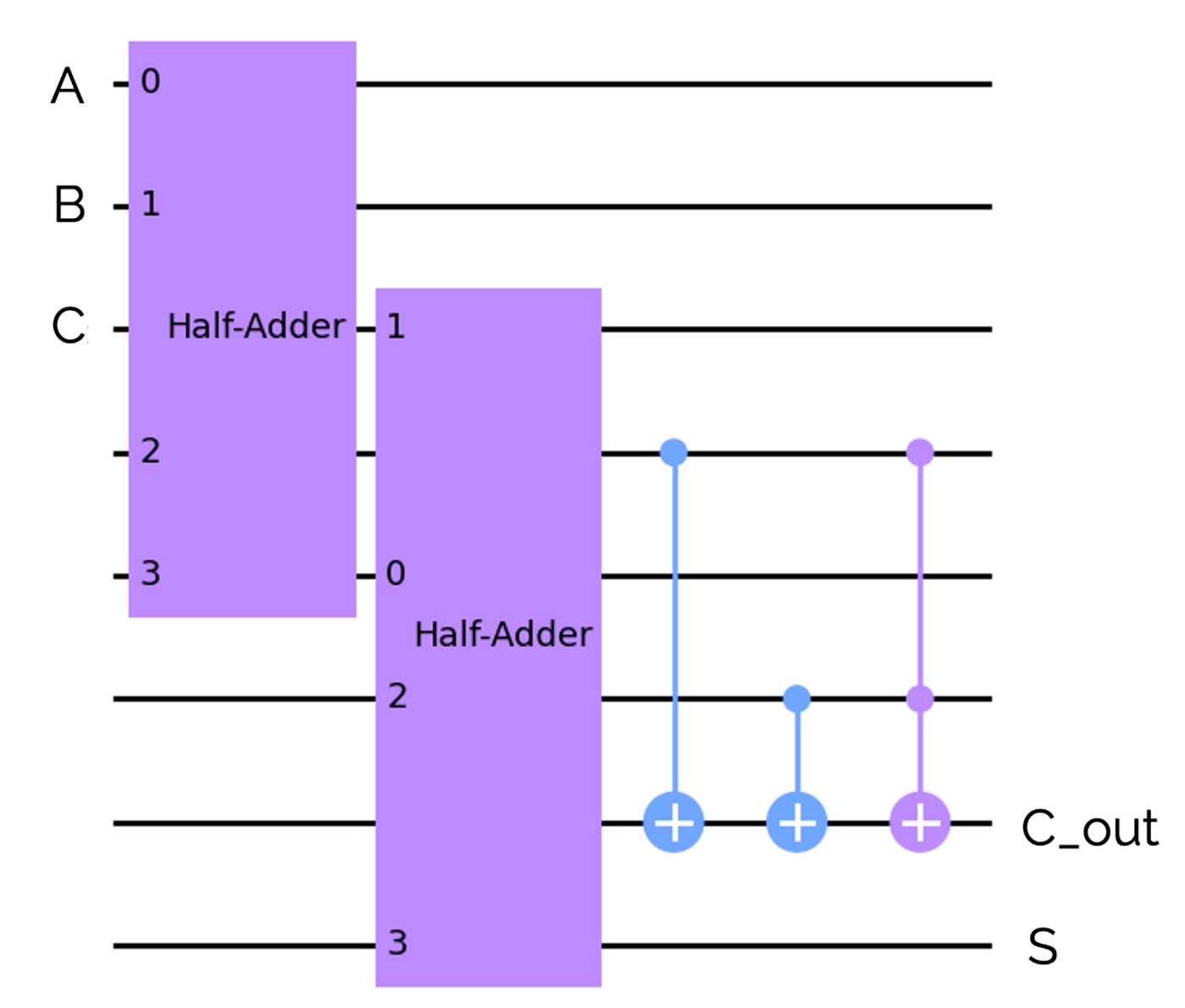
量子ゲート版

それでは、先ほど紹介した全加算器を量子ゲートに置き換えていきましょう。ORゲートと半加算器を使って全加算器を表現すると、下のようになります。

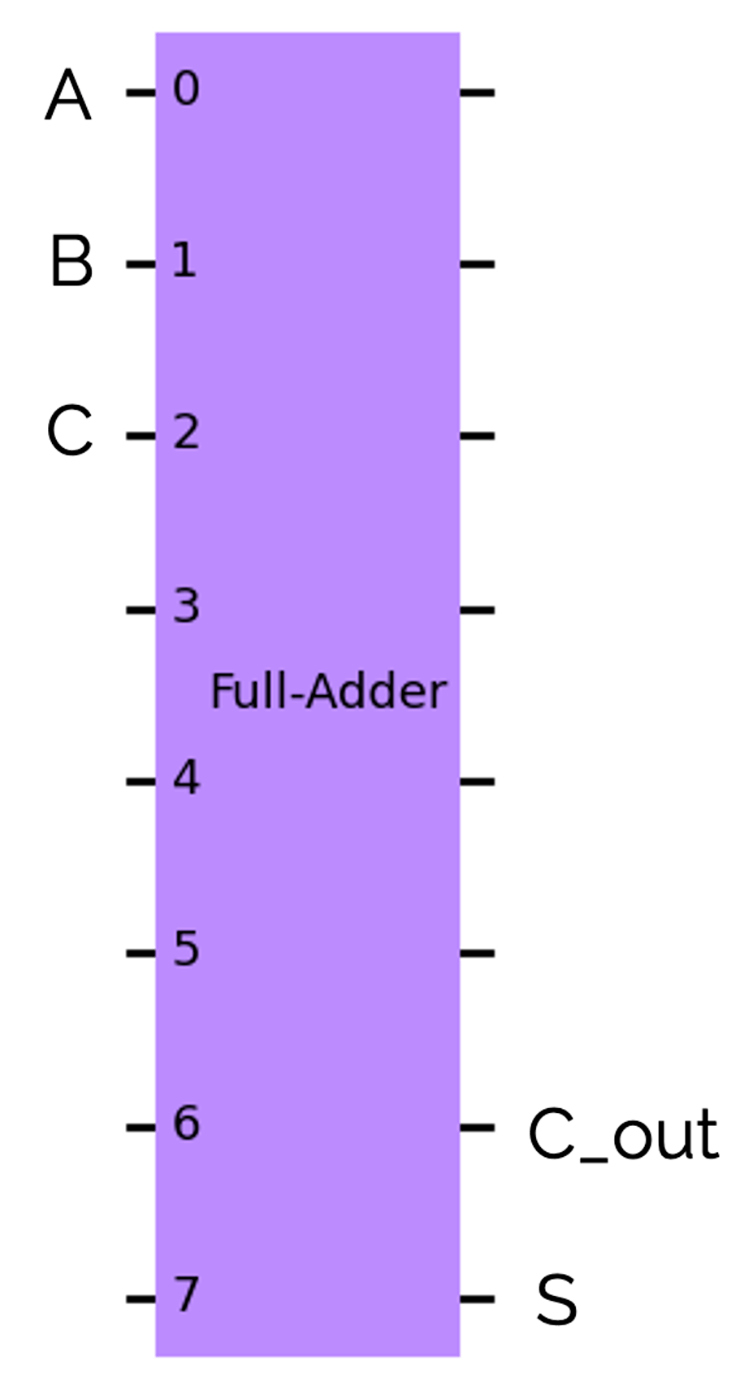
この回路は少し複雑なので、ここからは下のように省略して記述することにします。

意味を持つのは入力の$0, 1, 2(A, B, C)$ビットと出力の$6, 7(C_{out}, S)$ビットだけで残りは補助ビットです。

加減算器

2の補数表現

加減算器を実装する前に計算機における数の表現方法について解説します。数の表現方法には符号絶対値表現、補数表現、下駄ばき表現などがあります。今回は、補数表現のうちの2の補数表現を使っていきます。

2の補数表現における負の数の作り方は、正の数の2進数表現に対して$0, 1$反転して$1$を足すだけでできます。負の数から正の数への変換も同様の手順でできます。例えば$-5$を作る時は、$5=101_{(2)}$を$0, 1$反転して$010_{(2)}$、$1$を足して$011_{(2)}$が$-5$になります。この表現方法のメリットは引き算を負の数の足し算として計算できるため、これまでに作った加算回路をそっくりそのまま使える点です。実際に$7-5=7+(-5)$を計算すると、$111_{(2)}+011_{(2)}=1010_{(2)}$となり、はみ出た最上位ビットを無視すれば$010_{(2)}=2$なので正しく計算できていることがわかります。

古典版

それでは作った全加算器を拡張して、減算もできるようにしていきましょう。減算を行うときは$A-B$をするので$B$を$0, 1$反転して、繰り上がり入力から$1$を入力することで2の補数表現を再現します。すると、2ビットの加減算器は下のようになります。$X$に$0$が入ったときは、これまでと同様の全加算器です。対して$X$に$1$が入ると、$B$の正負が反転されて減算が実行されます。

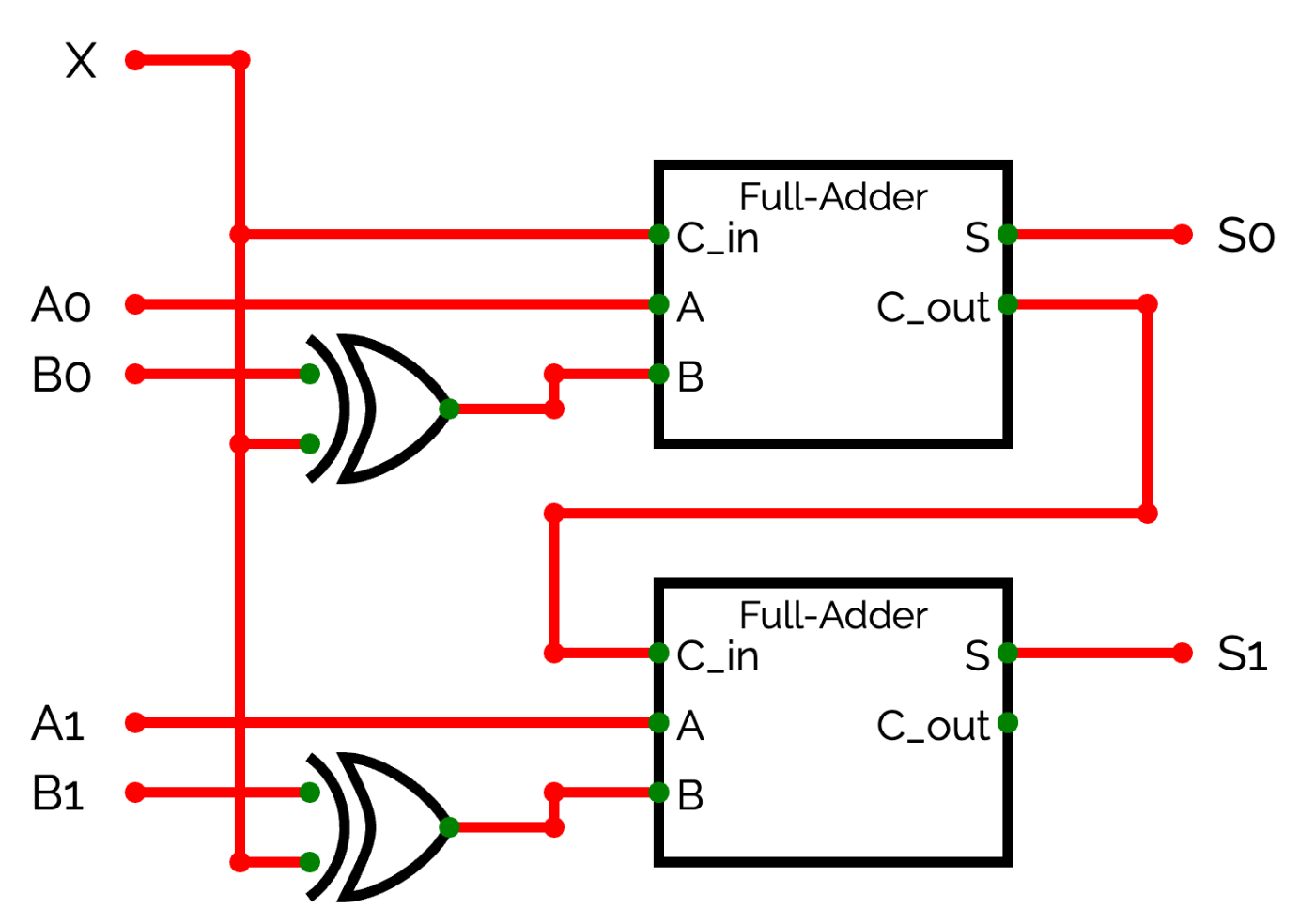
量子ゲート版

それでは、先ほど紹介した加減算器を量子ゲートに置き換えていきましょう。XORゲートと全加算器を使って2ビットの加減算器を表現すると、下のようになります。

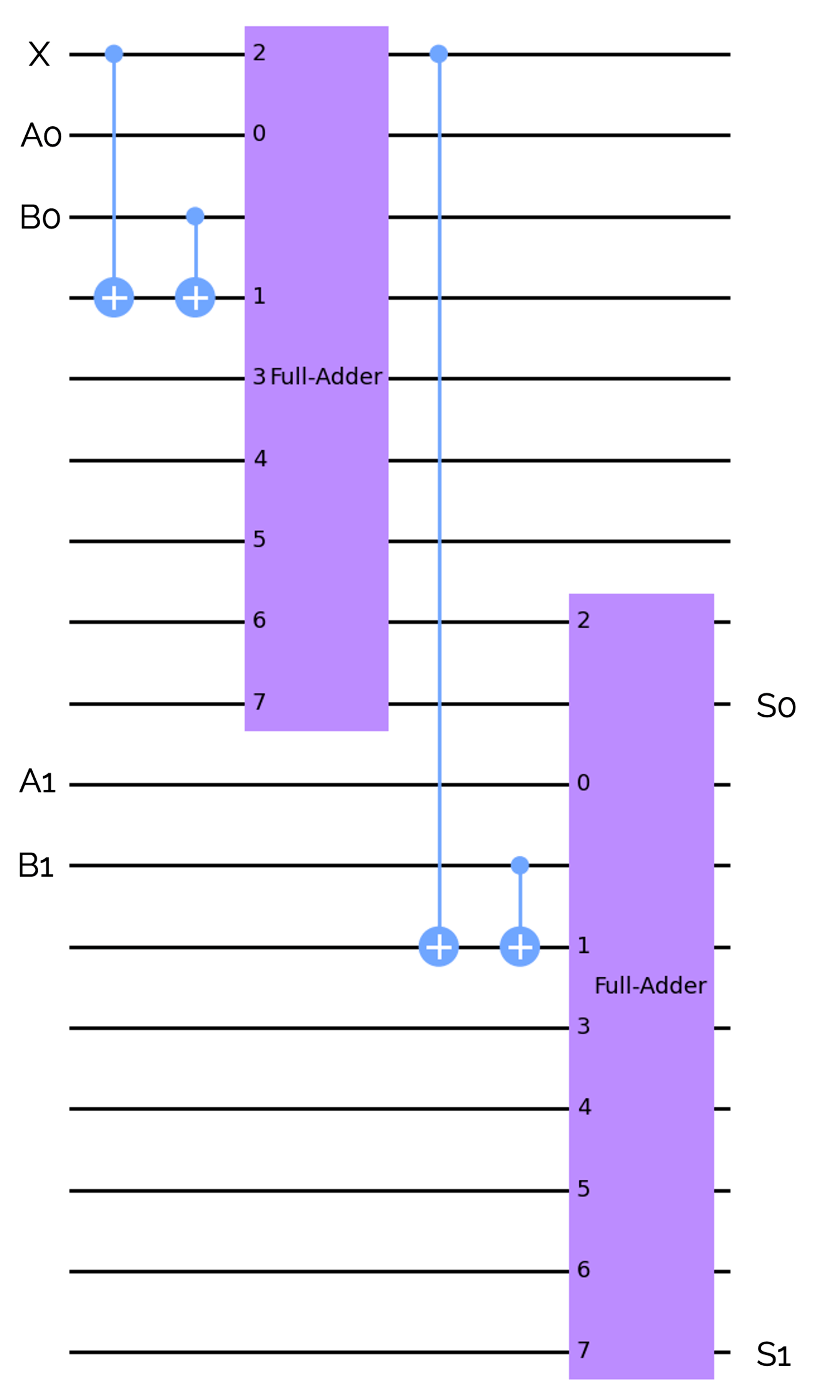
ALU

ついに、ALUの実装に入ります。今回実装するALUは、加算、減算、bitwise AND, bitwise OR, bitwise XOR, bitwise XNORが実行できるものを指します。

古典版

加算、減算については先ほど実装した加減算器が使えるので、これを拡張してAND, OR, XOR, XNORの演算をできるようにしていきます。

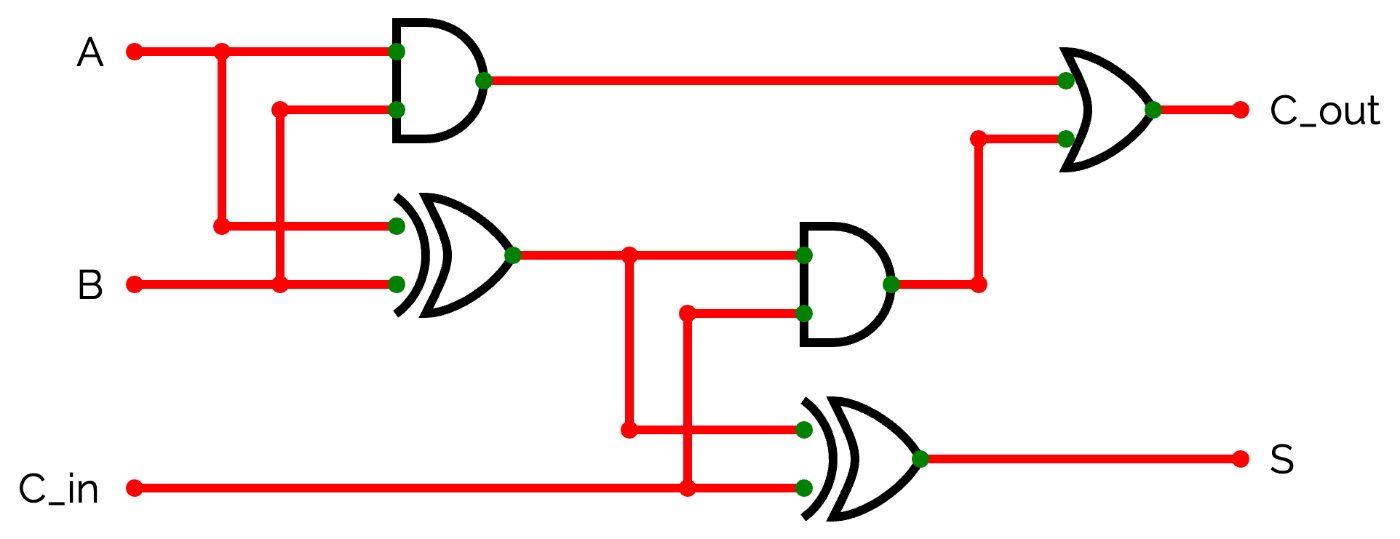
突然ですが、全加算器を半加算器の省略なしで書いた回路を上に示しました。この回路を論理式に変換すると、以下のようになります。

$$S = A \oplus B \oplus C_{in}\\ C_{out} = (A \cdot B) + ((A \oplus B) \cdot C_{in})$$

ここで、$C_{in}$の値を変えて$S, C_{out}$の出力を見てみると、

	$C_{in}=0$	$C_{in}=1$
$S$	$A \oplus B$	$\overline{A \oplus B}$
$C_{out}$	$A \cdot B$	$A + B$

のようになり、全加算器はAND, OR, XOR, XNORも出力することができることがわかります。

$C_{in}=1$のときに$C_{out}$が$A + B$となる理由が分かりづらいと思ったので、途中計算を示しておきます。

$$\begin{split} C_{out} &= (A \cdot B) + ((A \oplus B) \cdot 1)\\ &= (A \cdot B) + (A \oplus B)\\ &= (A \cdot B) + ((A \cdot \overline{B}) + (\overline{A} \cdot B))\\ &= (A \cdot B) + (A \cdot B) + (A \cdot \overline{B}) + (\overline{A} \cdot B)\\ &= (A \cdot (B + \overline{B})) + ((A + \overline{A}) \cdot B)\\ &= A + B \end{split}$$

そこで、ALUの演算を切り替える機能を追加するために、全加算器に制御ビット$W, X, Y, Z$を追加することで下のような回路になります。

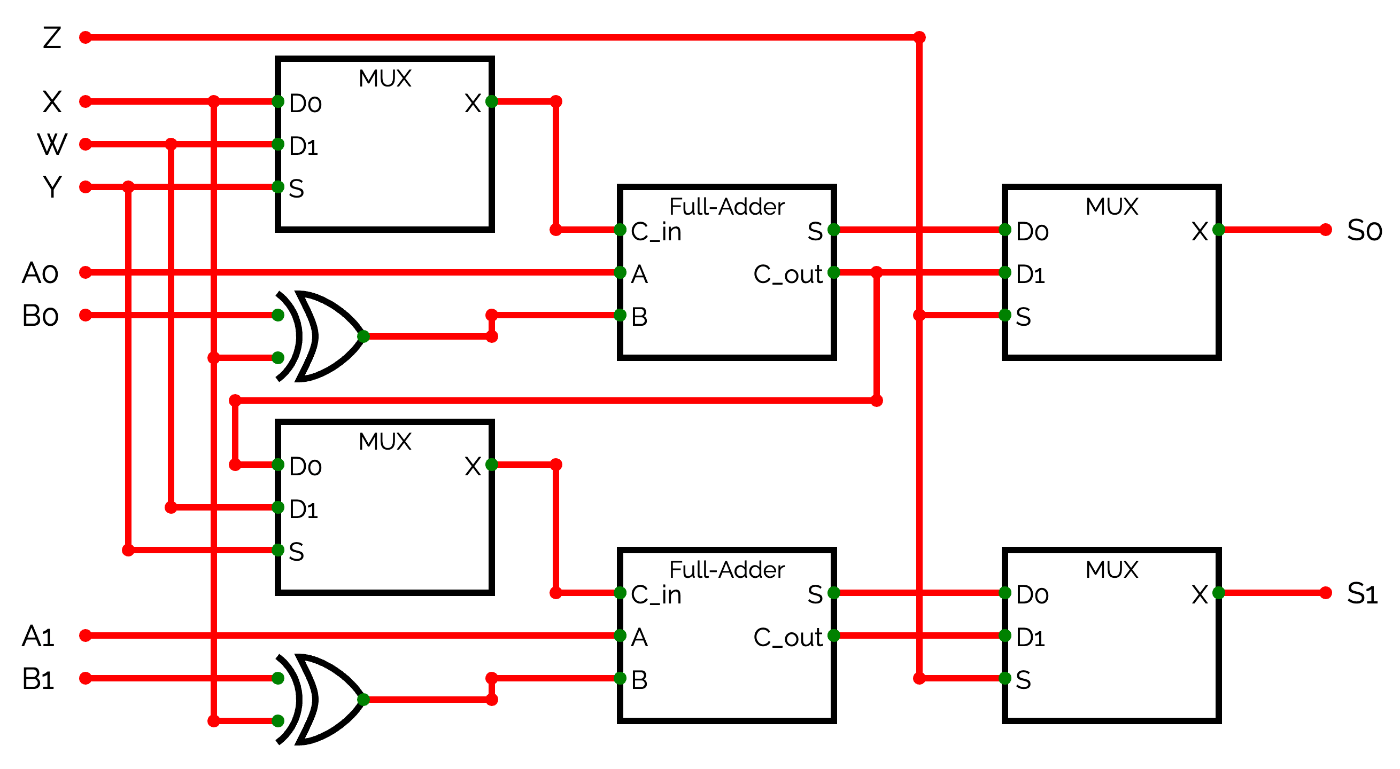
回路がかなり複雑に見えますが、加減算器にマルチプレクサとその制御ビットが追加されただけです。以下のように$W, X, Y, Z$を設定すると演算を切り替えることができます。

	$W$	$X$	$Y$	$Z$
ADD	$*$	$0$	$0$	$0$
SUB	$*$	$1$	$0$	$0$
AND	$0$	$0$	$1$	$1$
OR	$1$	$0$	$1$	$1$
XOR	$0$	$0$	$1$	$0$
XNOR	$1$	$0$	$1$	$0$

量子ゲート版

それでは、先ほど紹介したALUを量子ゲートに置き換えていきましょう。XORゲート、全加算器、マルチプレクサを使って2ビットのALUを表現すると、下のようになります。

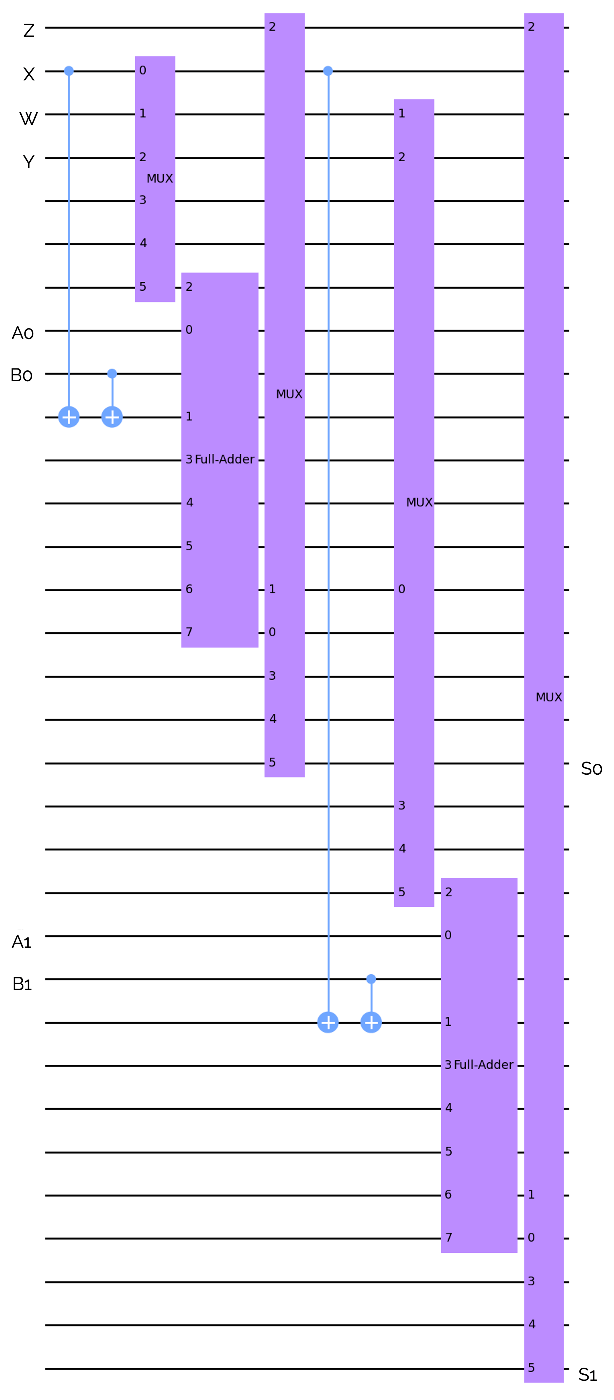
まとめ

この記事では、量子コンピュータを用いたALUの作り方について解説しました。ほとんど古典コンピュータにおけるALUの置き換えで作ることができました。
また、実際に量子コンピュータで計算する方法まで解説してしまうと非常に長くなってしまうため、次の記事にまわしたいと思います。

追記

実際に、実機の量子コンピュータに計算してもらう方法について解説した記事も書きました。
https://zenn.dev/luna_moonlight/articles/cd618bb1ee55e3