点推定、区間推定
参考:https://bellcurve.jp/statistics/course/8003.html
本来知りたいと思っている集団:母集団
母集団の情報を推測するために選ばれた集団:標本
母集団から一部を選んで標本とすること:抽出
母集団の資質を推測すること:推測統計学
参考:https://bellcurve.jp/statistics/course/8608.html?srsltid=AfmBOopn9oVQnZ-5oqyR369PGxdKP2l8pdtbhGduoxkPi-NkDgEKu5j_
推測統計学の中には推定と検定がある
日本人全員(母集団)から百人を抽出した標本を考える
点推定
参考:https://bellcurve.jp/statistics/course/8610.html
点推定:標本から母集団を特徴づけるパラメータ(母数)を推測する
例)
•全国の映画館の数を数えたい
•でも全部数えるの無理
•なので、10個の都道府県をチョイス
•その10個から平均を出す
-それを47都道府県の平均値とする(母平均点の推定)
- 大数の法則に従う
- 標本が大きくなるにつれて標本平均は母平均に近づく
推定量
•標本から母集団を特徴づけるパラメータ(母数)パラメータを推定するための計算式を推定量という
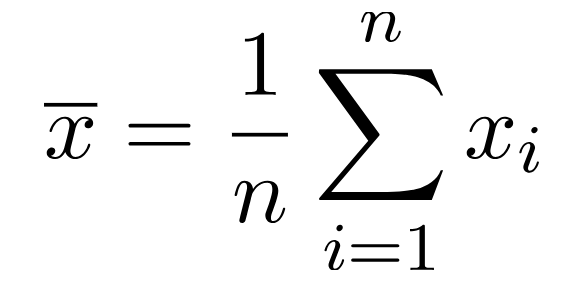
□推定量の問題
一致性
参考:https://bellcurve.jp/statistics/course/8612.html
•標本から母集団を特徴づけるパラメータ(母数)を推定するとき、その推測が正確である必要がある。
•標本の数が増えれば増えるほど、推定量がだんだんと真の値に近づく性質を一致性という
不偏性
参考:https://bellcurve.jp/statistics/course/8612.html
•標本から母集団を特徴づけるパラメータ(母数)パラメータを推定するための計算式である推定量の期待値がパラメータに一致している必要がある(予想と真の値はある程度一致している必要ある)。この性質を不偏性という。
標本分散
参考:https://bellcurve.jp/statistics/course/8614.html
•得られたデータの平均をxの平均、ここのデータをxi、サンプルサイズをn、標本分散をS^2

•でも、標本分散はnが十分に大きくないと、標本分散の期待値はぼ分散に一致せず、母分散より小さくなる
不偏分散

•標本分散の期待値が母分散に一致するようにする
- 標本分散の算出式にn/n-1をかけたものが不偏分散の算出式となる

- n/n-1をかけたものが不偏分散の算出式となるか?:標本分散が母分散の推定値として偏りがあるので、それを補正する(不偏=偏りがない)ため
- 標本平均を計算に使うことで、標本分散は母分散の下限推定値になりがち
- 下限推定値:
- 標本分散は母分散を推定するとき、いつも値が少し小さくなってしまう傾向がある。
- なので、この偏りを補正するために不偏分散を使う
標準誤差
参照:https://bellcurve.jp/statistics/course/8616.html
•標準誤差:標本から母集団を特徴づけるパラメータ(母数)パラメータを推定するための計算式を推定量の標準偏差
•標本から得られる推定量そのもののバラつき(=精度)
•標本誤差は標本平均の標準偏差(バラつき具合)を表す
•平均μ、分散に従う母集団からサンプルサイズnの標本を抽出するとき、その平均値xの分布はnが大きくなるつれて
•標本を抽出するとき、その平均値xの分布はnの標本が大きくなるにつれて、正規分布に近づく(標本サイズが大きいと正規分布に近づく)
区間推定/点推定
参考:https://www.youtube.com/watch?v=a4w0pVnivjQ
- 点推定:100人の日本人男性の身長を調べてみると、平均が174cmだったので、全国の日本人男性の平均身長も174cmとすること。
- 区間推定:100人の日本人男性の身長を調べてみると、平均が174cmだったので、全国の日本人男性の平均身長は少し幅を持たせて172cmから176cmとすること。
- 母集団からサンプルを抜き出してそれを標本とする際、100回中95回は母集団の平均内にある値が入るだろう!とするのが、区間推定でこの区間が「95%信頼区間」
- 95%より、99%の方が幅が広い
- 理由:99%は「母集団の平均値の99%が標本にもふくまれている」という意味だから、その分守備範囲も広くなる。
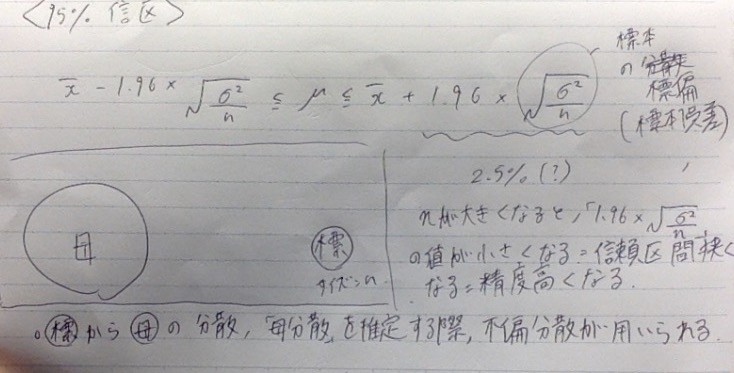
- 理由:99%は「母集団の平均値の99%が標本にもふくまれている」という意味だから、その分守備範囲も広くなる。
練習問題
参照:https://bellcurve.jp/statistics/course/11065.html
(1)

解説
-「X~」の計算式は「確率変数Xは平均がμで、分散が25である正規分布に従う」ことを意味している。

Discussion