ヒープソートアルゴリズムとは(定義,利点・欠点,計算量,安定アルゴリズムか)
1.定義
ヒープソートとは未整列データをヒープの性質を持った木構造で、最大値、最小値を抽出して取り出す、という作業を繰り返すソートアルゴリズムだ。5,9,5,6,3,8,6,2という配列を用いて例を示す。
【処理1】
まず、この未整列データを木構造で表現するとこのようになる。
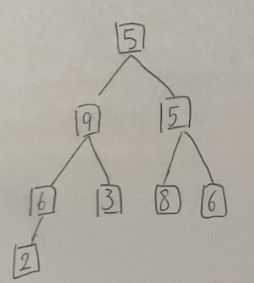
まず一番下の葉を比較する。木構造は親ノード≥子ノードという構造である必要があり、下記の6,2は6(親ノード)≥2(子ノード)となっているので、このままとする。
次に上のグループを比較する。
ここでは、親ノード9は子ノード6,3よりも大きいため、このままとする。
次に隣のグループを比較する。
親ノード5は、子ノード8,6より小さいため、子ノードで一番大きい8を5と入れ替える。

次に一番上のグループを比較する。
親ノード5は子ノード9,8より小さいので、子ノードで最も大きい9を5と入れ替える。

そして、5が移動してきたグループをみると、親ノード5は子ノード6よりも小さいため、入れ替える。

一番上の根が最大値になり、木構造の並び替えは完了したため、整列済みデータに最大値の9を追加する。
整列済みデータ:9
【処理2】
そして、次に整列済みデータとなった9を除いた未整列データで木構成を作る。ここで、一番下の2を一番上に持っていく。そして、一番下の値を一番上に持っていったからといって親ノード≥子ノードとなっている保証はないので、ノードの順番を確認する。

すると子ノード8が一番大きいので8と2を入れ替える。

次に、入れ替えた右側のグループをみると6が一番大きいので2と6を入れ替える。

ここで木構造の作成が完了したので、ルートの値を整列済みデータに追加すると、整列済みデータは以下のようになる。
整列済みデータ:8,9
【処理3】
整列済みデータとなった8を除いた未整列データで再び木構造を作る。そのため、一番下の2を一番上に持っていく。

一番上のグループをみると、親ノード≥子ノードとなっていないので、2と6を入れ替える。

入れ替えた右側グループをみると、親ノード2より子ノード5の方が大きいので、入れ替える。

ここで、一番上に最も大きい数字6がきたので、木構造の作成が完了した。そのため配列済みデータに最大値の6を追加する。
配列済みデータ:6,8,9
【処理4】
ここでは、一番下の2を一番上に持っていく。
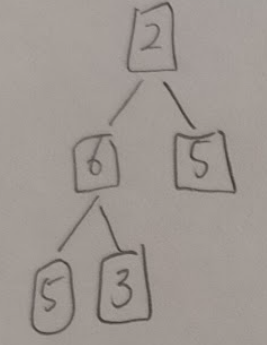
すると、一番上の親ノード2より子ノード6,5の方が大きいので子ノードの中で一番大きい6を2と交換する。

左側のグループをみると、親ノード2が子ノード5,3より小さいことがわかるので、子ノードの中で大きい方の5を2と入れ替える。

これで木構造の整列は完了し、一番上の6を配列済みデータに追加する。
配列済みデータ:6,6,8,9
【処理5】
一番下の3を一番上に持ってくる。

すると、一番上のグループで親ノード3より子ノード5の方が大きいことがわかったので、3と5を入れ替える。

これで木構造の作成が完了したので、一番上の5を配列済みデータに追加する。
配列済みデータ:5,6,6,8,9
【処理6】
一番下の2を一番上に持っていく。

すると、子ノード5が親ノード2より大きいので入れ替える。

これで木構造の整列が完了したので、5を整列済みデータに追加する。
配列済みデータ:5,5,6,6,8,9
【処理7】
残りの2つのノードのうち、3を親ノードにすると、木構造の作成が完了していることがわかる。

そのため、3を配列済みデータに追加するとともに、ノードが2のみになるので、こちらも配列に追加する。
配列済みデータ:2,3,5,5,6,6,8,9
このようにしてヒープソートは処理される。
2.計算量の算出
ヒープを再構成する際に必要な計算量はlog2nで表される。以下の木構造を用いて説明する。

3が新たなデータとして追加されたとすると、3,5の順番が適切かという処理と、ここでは3と5が入れ替わるので、入れ替わった時、3,2の順番が適切かという2回の処理が必要である。つまり計算式で表すと、ノードが4つあるのでn=4となり、すなわち、log2の4=2回の処理が必要だということだ。そして、仮にn個のデータが追加されると、その分計算量が増えるので、計算量はlog2n ✖︎ nとなる。これは、データを取り出すときにも同様である。つまり、データを取り出したあとも、ヒープは再構成される。例えば「1.選んだアルゴリズムはどのようになっているか」で示した例でも以下のような木構造から、6が取り除かれるときを考える。

その際、6が取り除かれると、一番下の3が一番上に行くので、木構造は以下のようになる。

この時も、3,5の順番が適切かという処理と、ここでは3と5が入れ替わるので、入れ替わった時、3,2の順番が適切かという2回の処理が必要である。つまり計算式で表すと、ノードが4つあるのでn=4となり、すなわち、log2の4=2回の処理が必要だということになる。よって、要素を追加する時と要素を取り出す時の両方を考慮すると計算量は、
nlog2のn+nlog2のn = 2nlog2のn となり、つまりオーダー記法で記述すると定数部分は無視されるのでO(nlog2のn)となる。
3.安定アルゴリズムであるか否か
ヒープソートは安定ソートではない。例を用いて示す。仮に配列、3A,5,3B,1というものがあり、3A=3Bというための要素があるとする。これをまず、木構造で表現するとこうなる。

そして、親ノード3Aより子ノード5の方が大きいので、入れ替わる。

これで木構造は完了したので、一番上のノード5が配列済みデータに追加される。
配列済みデータ:5
その後、一番下の1が一番上にいくので、このようになる。

ここで問題となるのが、3A,3Bどちらを親ノード1と比較をし、並び替えるのかということだ。3A=3Bのため、親ノードに3A,3B両方を持っていくことができるパターンがある。そのため、最終的な配列済みデータは1,3A,3B,5と1,3B,3A,5という2通りある。後者の配列の場合、3A,5,3B,1という最初の配列での3A,3Bとは順序がことなる。故にヒープソートは不安定であるといえる。
4.Cによる実装例
ソースコード
#include<stdio.h>
/* 値を入れ替える関数 */
void swap (int *x, int *y) {//2つの値を
int temp; // 値を一時保存する変数
temp = *x;
*x = *y;
*y = temp;
}
/* pushdouwn操作 */
void pushdown (int array[], int first, int last) {
int parent = first; // 親
int child = 2*parent; // 左の子
while (child <= last) {
if ((child < last) && (array[child] < array[child+1])) {
child++; // 右の子の方が大きいとき、右の子を比較対象に設定
}
if (array[child] <= array[parent]) { break; } // ヒープ済み
swap(&array[child], &array[parent]);
parent = child;
child = 2* parent;
}
}
/* ヒープソート */
void heap_sort (int array[], int array_size) {
int i;
for (i = array_size/2; i >= 1; i--) {
pushdown(array, i, array_size); // 全体をヒープ化
}
for (i = array_size; i >= 2; i--) {
swap(&array[1], &array[i]); // 最大のものを最後に
pushdown(array, 1, i-1); // ヒープ再構築
}
}
int main (void) {
int array[11] = { 0, 2, 1, 8, 5, 4, 7, 9, 10, 6, 3 };
int i;
printf("Before sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
heap_sort(array, 10);
printf("After sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
return 0;
}
実行結果
Before sort: 2 1 8 5 4 7 9 10 6 3
After sort: 1 2 3 4 5 6 7 8 9 10
解説
/* 値を入れ替える関数 */
void swap (int *x, int *y) {//2つの値を
int temp; // 値を一時保存する変数
temp = *x;
*x = *y;
*y = temp;
}
swap関数とは2つの値を入れ替える関数だ。int *xとint *yは入れ替えたい値を指すポインタだ。関数内で直接値を変更するため、実際のメモリ1を操作する。こうすることで、呼び出し元の値も更新される。
int temp;は値を一時保存する変数であり、入れ替え処理で一方の値が上書きされるのを防ぐ。
temp = *x;はポインタxが指す値をtempに保存する。こうすることとで、*xの値が他の値で上書きされても元の値が失われない。
*x = *y;はポインタyが指す値をポインタxが指す位置に代入する
*y = temp;はtempの保存しておいた元のxの値をポインタyが示す位置に代入する
/* pushdouwn操作 */
void pushdown (int array[], int first, int last) {
int parent = first; // 親
int child = 2*parent; // 左の子
while (child <= last) {
if ((child < last) && (array[child] < array[child+1])) {
child++; // 右の子の方が大きいとき、右の子を比較対象に設定
}
if (array[child] <= array[parent]) { break; } // ヒープ済み
swap(&array[child], &array[parent]);
parent = child;
child = 2* parent;
}
}
pushdownは二分木の親ノードと子ノードの関係を調整する。
while (child <= last) {では子ノードが配列の範囲内に存在する間、処理を続ける
if ((child < last) && (array[child] < array[child+1])) {
child++; // 右の子の方が大きいとき、右の子を比較対象に設定
}
child < lastでは、親ノードと比較する対象を決定する。
array[child] < array[child+1]では、親ノード≥子ノードを達成するため、ノードを比較している
if (array[child] <= array[parent]) { break; } // ヒープ済み では親ノード≥子ノードという条件を満たしているかを確認する
swap(&array[child], &array[parent]);
parent = child;
child = 2 * parent;
ここでのswapは親と子の値を入れ替える
parent = childで子ノードを親ノードとして設定する
child = 2 * parent; でノードに対する左の子ノードのインデックスを計算する。ここでは左の子のインデックスは
現在の親ノードが更新された後、その新しい左の子ノードをを計算するためのものだ。例えば以下のような二分木があった場合、child = 2 * parent;は左の子ノード、child = 2 * parent + 1;は右の子ノードを表現している。
10 (index 1)
/
5 (2) 8 (3)
/ \ /
3(4) 7(5) 2(6)
/* ヒープソート */
void heap_sort (int array[], int array_size) {
int i;
for (i = array_size/2; i >= 1; i--) {
pushdown(array, i, array_size); // 全体をヒープ化
}
for (i = array_size; i >= 2; i--) {
swap(&array[1], &array[i]); // 最大のものを最後に
pushdown(array, 1, i-1); // ヒープ再構築
}
}
heap_sort関数はヒープ化、ソートの2つの処理を行う。配列全体を最大ヒープの形に変換する。ソートではヒープの最大値(親ノード)を取り出し、配列の末尾に配置する。
ヒープ化の準備として、のコードが以下である。
for (i = array_size/2; i >= 1; i--) {
pushdown(array, i, array_size); // 全体をヒープ化
}
ここでは配列を最大ヒープに変換する。配列サイズがarray_sizeのとき、最後の親ノードはarray_size/2に位置する。
for (i = array_size / 2; i >= 1; i--) というループでは、ヒープの最後の親ノード(array_size / 2)からスタートし、インデックスが1まで逆順に進む。この順序は「下位の部分木から順番に」処理することを意味している。以下の木構造を用いて説明する。
10 (index 1)
/ \
5 (2) 8 (3)
/ \ \
3 (4) 7 (5) 2 (6)
まずは右下のグループを対象の部分木とする。
8
2
子ノード2は親ノード8より小さいので交換はない。
次の親ノードは左下のグループだ。
5
/
3 7
ここでは右の子7が最大なので、親ノード5と交換される。
このように、回の部分木から順番に処理することをfor (i = array_size / 2; i >= 1; i--) では表現している。
最後に、以下のコードについて解説する。
int main (void) {
int array[11] = { 0, 2, 1, 8, 5, 4, 7, 9, 10, 6, 3 };
int i;
printf("Before sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
heap_sort(array, 10);
printf("After sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
return 0;
}
配列arrayは要素数11の整数配列だ。
int array[11] = { 0, 2, 1, 8, 5, 4, 7, 9, 10, 6, 3 };
int i;
上記コードにおいて、なぜインデックス0に0を配置するのかについて説明する。
次の配列を考える。
要素0あり
配列: array = [0, 10, 20, 15, 30, 40]
要素0なし
配列: array = [10, 20, 15, 30, 40]
このとき、要素0が配列のヒープ構造は以下のようになる。
10 (index 1)
/
20 (2) 15 (3)
/
30 (4) 40 (5)
このとき、親子関係の計算例を示すと、親ノード(index = 1)の子ノードに関して「左の子ノード」 は
2×1=22 ✖︎ 1 = 22×1=2
と計算でき、値は 20だ。
「右の子ノード」は
2×1+1=32 ✖︎ 1 + 1 = 32×1+1=3
と計算でき、値は 15だ。
親ノード(index = 2)の子ノードに関しては、「左の子ノード」 の計算は
2×2=42 ✖︎ 2 = 42×2=4
となり、値は 30となる。
「右の子ノード」に関しては
2×2+1=52 ✖︎ 2 + 1 = 52×2+1=5
となり、値は 40となる。
要素0なしの場合だと、ヒープ構造は以下のようになる。
10 (index 0)
/ \
20 (1) 15 (2)
/ \
30 (3) 40 (4)
その際、親子関係の計算例は、親ノード(index = 0)の子ノードについては、「左の子ノード」は
2×0+1=12✖︎0 + 1 = 12×0+1=1
で、値は 20となる。
「右の子ノード」は
2×0+2=22✖︎0 + 2 = 22×0+2=2
で、値は 15となる。
親ノード(index = 1)の子ノードの「左の子ノード」は、2×1+1=32✖︎1 + 1 = 32×1+1=3
となり、値は 30となる。
「右の子ノード」は
2×1+2=42✖︎1 + 2 = 42×1+2=4
となり、値は 40である。
このように、要素0がある場合だと、計算が2×iや2×i+1とシンプルな式で表現ができる。一方、要素0を用いないと、式に+1や+2が含まれ、計算が複雑化し、エラーリスクが増大してしまう。このような計算のしやすさという観点から、要素0を用いている。
printf("Before sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
ソート前の配列であるBefore sort: 2 1 8 5 4 7 9 10 6 3を表示する。
heap_sort(array, 10);でheap_sort関数を呼び出してarrayのインデックス1から10をソートする。
printf("After sort: ");
for (i = 1; i < 11; i++) { printf("%d ", array[i]); }
printf("\n");
こちらでは、ソート後の配列を出力し、出力は
After sort: 1 2 3 4 5 6 7 8 9 10
となる。
5.バブル、選択、挿入ソート、クイックソートと比べたときのヒープソートアルゴリズムの利点・欠点
メリットとしては、処理スピードの速さだ。バブル、選択、挿入ソート、クイックソートの最悪の計算量はO(n^2)であるが、ヒープソートは最悪でもO(n log n)の計算量なのでそれらよりもヒープソートは処理が早いことがわかる。また、最悪の計算量が同じマージソートに比べてヒープソートはメモリの使用量が少ないため、マージソートと比べデータ数が大きい場合の処理に向いている。
デメリットとしては、バブルソート、選択ソート、挿入ソートに比べ、アルゴリズムが複雑で実装が難しいことだ。また、デメリットとは言えないが、クイックソートや選択ソート同様、ヒープソートは不安定ソート順序が重要なデータには不向きだ。
参考文献
株式会社インフラトップ「アルゴリズムの代表的な種類一覧|それぞれの特徴を徹底的に解説」https://web-camp.io/magazine/archives/110411/(2024年12月30日アクセス)
三重大学「データ構造・アルゴリズム論 ヒープの操作手順」https://www.cs.info.mie-u.ac.jp/~toshi/lectures/algorithm/heap.pdf(2025年1月2日アクセス)
【メモ】
選択ソート、 バブルソート、挿入ソート、マージソート、ク イックソート
【ヒープソート】
ヒープソートの計算時間は、最悪ケースを考慮しても以下の通りとされています。
O(n log n)
不安定
【計算量】
バブル:O(n^2)、必ずn(n-1)/2回の比較が行われます。
選択:O(n^2)、交換回数は多くてもn-1回であり、バブルソートよりも高速
マージ:最悪ケースでもO(n log n)
挿入:比較回数は、最悪の場合にn(n-1)/2(=O(n^2))。ソート済み部分が多いとより有効なアルゴリズム
クイック:平均でO(n log n)ですが、最悪のケースではO(n^2)
ヒープ:最悪でもO(n log n)
【安定・不安定】
バブル:安定
挿入:安定
マージ:安定
選択:不安定
クイック:不安定
ヒープ:不安定
計算量:O(n^2)よりO(n log n)の方が早い
【バブル・選択・挿入】
シンプルで実装簡単
【本文】
ヒープソートはソートが高速であり、かつ、マージソート等に比べてメモリの使用量が少ない。そのため、データ数が多い場合に強みを発揮する。ただ、単純選択ソートや単純挿入ソートに比べるとアルゴリズムが少し複雑で難しいというデメリットもあえう。なお、クイックソートと同様に安定していないソートになります。
Discussion