超関数型プログラミング

この記事はFOLIO Advent Calendar 2022の23日目です。

ソフトウェア2.0

ソフトウェア2.0 という新しいプログラミングのパラダイムがあります。これは Tesla 社のAIのシニアディレクターだった Andrej Karpathy が自身のブログ記事（"Software 2.0"）で提唱した概念で、 ニューラルネットワーク のような最適化を伴うプログラムを例に説明されています。

従来のプログラム（Software 1.0）は人間が命令に基づいたプログラムを作成し、望ましい挙動を行わせます。それに対してニューラルネットワークのようなプログラム（Software 2.0）では人間はある程度の自由度をパラメータという形で残したプログラムを作成し、「入出力のペア」や「囲碁に勝つ」というような教師データや目的を与えてプログラムを探索させるというものです。

画像出典: "Software 2.0"

この考え方はニューラルネットワークのような微分可能で勾配降下法によって最適化されるプログラムだけに留まらず、その他の統計的機械学習も含むような帰納プログラミングの文脈で語られることもあります。例えばMLSS (Machine Learning Summer School)2014で行われた確率的プログラミング^[1]についての講演では以下のスライドを使って確率的プログラミングの説明がされています。

画像出典: Probabilistic Programming and Bayesian Nonparametrics -- Frank Wood (Part 1)

従来のプログラムの考え方（左）が

パラメータを決めてプログラムからアウトプットを得る

ものだったのに対し、確率的プログラミングの考え方（右）が

観測データとプログラムからパラメータを得る

という逆の順に帰納的に辿っていることが分かりやすいかと思います。

微分可能プログラミング

話をニューラルネットワーク（微分可能プログラミング^[2]）に戻しましょう。

現在ディープラーニングでよく用いられている活性化関数として ReLU があります。

ReLU は以下のような式で表される関数です。

$${\rm ReLU}(x) = \begin{cases} 0 && \ \ x < 0 \\ x && \ \ x \geq 0 \\ \end{cases}$$

グラフで書くと以下のような形になります。

この関数は微分可能プログラミングの文脈でよく使われますが、よく見ると原点の部分で折れ曲がっており微分可能ではありません。

原点での微分の値が定まらないなら適当に決めてやれば（だいたい0か1）大丈夫でしょうか？しかしこの場合、原点における微分の値を $a$ と置くと $x + {\rm ReLU}(-x)$ は関数の値が ${\rm ReLU}(x)$ と一致するにも関わらず原点における微分の値が $1 - a$ になるというような奇妙な関数を作れてしまいます^[3]。

ニューラルネットワークのパラメータなんて普通は初期値を確率的に設定するから^[4]1点における微分の値が問題になることは無いのでは？（確率が0）と思うかもしれませんが、このように厳密には挙動が定まっていないような考え方を用いるとプログラムの正しさを証明するというような形式的な議論をすることが困難になるという問題があります。Software 2.0のように新しいプログラミングパラダイムとしての地位を確立していくのであれば形式的な理論の土台をしっかり作っておくことは、なおさら重要な課題になるでしょう。

そこでReLUのような（通常の意味では）微分が出来ない関数も数学的に厳密に扱いたいという欲求が出てくるわけです。数学において、このような通常の意味では微分できないような関数の微分を扱える理論の一つに 超関数論 と呼ばれる分野があります。

ところで、ここで一つ種明かしをしておきますと、この記事のタイトルは「超関数型プログラミング」となっていますが、これは

"超"関数型プログラミング

と区切るのではなく

"超関数"型プログラミング

と区切るのが正解です（ちなみに「超関数型プログラミング」は私が勝手に作った造語ですので悪しからず（´(ｪ)｀））。

今年の7月にこの超関数を使って上記のような 通常の意味では微分が出来ないような関数の微分も扱えるようなプログラム（ラムダ計算）を考える といった論文 "Distribution Theoretic Semantics for Non-Smooth Differentiable Programming" が公開されており、以下ではこの論文で提案されている $\lambda_\delta$ という計算体系について簡単に紹介したいと思います。

超関数論

まず初めに超関数論について数学的な観点から簡単に説明したいと思います。いわゆる超関数論にはシュワルツの超関数(Schwartz distributions)と佐藤超函数(Hyperfunctions)の二つの理論がありますが、ここでは シュワルツの超関数 を扱います。

超関数論で扱える有名な関数としてディラックのデルタ関数があります。これは以下のような性質が期待される"関数"です。

$$\begin{matrix} \delta(x) &=& &0& \ \ (x \neq 0) \\ \displaystyle\int_{-\infty}^\infty \delta(x)dx &=& &1& \\ \end{matrix}$$

要するに原点以外の値はべったり0になっているけれど、実数全体で積分すると1になるという性質を持つ"関数"です。"関数"とカッコ付きになっているのは上記２つの性質を満たす普通の関数(実数から実数への関数)は存在しないからで、上記の性質を満たそうと思うとある意味 $\delta(x) = \infty$ とならなければいけませんが $\infty$ は実数ではありません。

なぜこの様な性質を持つ"関数"を考えたくなるのでしょうか。元々は量子力学を定式化するために広がりを持たない点粒子をモデル化する目的として導入されたのですが、ここでは別の話として確率分布を例に考えてみましょう。以下の図は平均値が0である正規分布の確率密度関数の分散の値を0に近づけた時の様子を図示したものです（青線: $\sigma = 0.5$, 緑線: $\sigma = 0.2$, 赤線: $\sigma = 0.1$）。

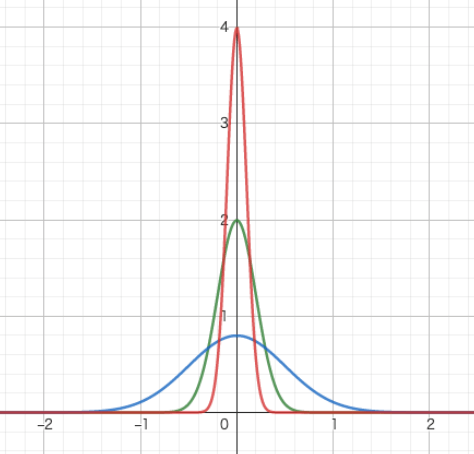
見て分かる通り分散を0に近づけると $x\neq 0$ の部分で確率密度関数の値は0に近づくことが分かります。更に確率密度関数であることから実数全体で積分した値は分散を変えても1のままです。残念ながら $\sigma$ をピッタリ0にすると0除算が発生するため考えることが出来ませんが、デルタ関数はまさにこの $\sigma = 0.0$ の正規分布のような存在であり、実際に極限の操作を用いてそのように構成することが可能です。デルタ関数はこのように確率分布として原点に値を取る確率が100%であることを表す実数上の確率分布と解釈することができますが、これを応用すれば例えば $0.5\delta(x) + 0.5\delta(x-1)$ という式で50%の確率で0か1を取る実数上の確率分布を表せる等、応用上も便利で欠かせない存在になっています。

もう一つ重要なデルタ関数の性質として、実数から実数への連続関数 $f(x)$ に対して

$$\int_{-\infty}^\infty f(x)\delta(x)dx = f(0)$$

が成り立つ、というものがあります。この性質は既存の性質から導くことが出来ますが、反対に$f(x)$として恒等的に1になるような定数関数を考えれば、この性質からデルタ関数の実数全体での積分が1になるという性質を復元することも出来ます。この性質はデルタ関数を使って与えられた関数 $f(x)$ に実数 $f(0)$ を対応させる汎関数（関数を取って実数を返す関数）を表していると解釈することができ、デルタ関数に限らずシュワルツの超関数はその様な方法で定義されているのです。

シュワルツの超関数については既に多くの文献が存在するので入門的な内容についてはそちらを参考にしてください。

• 超関数論への誘い　15分でわかる超関数の考え方
• 超関数入門 - 物理のかぎしっぽ
• 微分積分と線型代数と簡単な集合位相で学ぶ超関数超入門

これ以降は

• 超関数の定義
• 超関数の微分の定義

が分かっていれば読み進めることが可能です。

まずはReLUを2回微分するとデルタ関数になることを確認してみたいと思います。

改めて ReLU の定義はこちらです。

$${\rm ReLU}(x) = \begin{cases} 0 && \ \ x < 0 \\ x && \ \ x \geq 0 \\ \end{cases}$$

ReLUは局所可積分（任意のコンパクト部分集合上でルベーグ可積分）なので、ReLUを持ち上げた超関数$T_{\rm ReLU}$を考えることが出来ます。これは任意のテスト関数$\phi$に対して以下のような汎関数を考えることに対応します。

$$\langle T_{\rm ReLU}, \phi \rangle = \int_{-\infty}^\infty {\rm ReLU}(x)\phi(x)dx$$

それではこの$T_{\rm ReLU}$を微分してみましょう。

$$\begin{matrix} \langle \frac{dT_{\rm ReLU}}{dx}, \phi \rangle &=& -\langle T_{\rm ReLU}, \frac{d\phi}{dx} \rangle \\ &=& -\int_{-\infty}^\infty {\rm ReLU}(x)\frac{d\phi}{dx}dx \\ &=& -\int_0^\infty x\frac{d\phi}{dx}dx \\ &=& -[x\phi(x)]_0^\infty + \int_0^\infty \phi(x)dx \\ &=& \int_0^\infty \phi(x)dx \\ &=& \langle H, \phi \rangle \\ \end{matrix}$$

• 1行目が超関数の微分の定義
• 2行目は汎関数として対応する積分計算
• 3行目はReLUの定義を展開
• 4行目は部分積分
• 5行目は第一項を評価
• 6行目はヘヴィサイド関数の定義より

このようにReLUを微分する（正確には持ち上げた超関数を微分する）とヘヴィサイド関数 $H$ が現れることが分かります。ヘヴィサイド関数は超関数ですが（原点を除いて）関数として表すと以下のようになります。

$$H(x) = \begin{cases} 0 && \ \ x < 0\\ 1 && \ \ x > 0 \\ \end{cases}$$

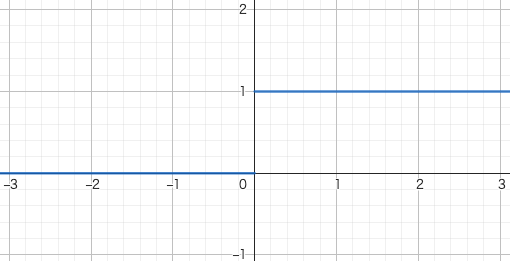
このヘヴィサイド関数を微分するとデルタ関数が出てくることは有名な話ですがせっかくなので実際に見てみましょう。

$$\begin{matrix} \langle \frac{dH}{dx}, \phi \rangle &=& -\langle H, \frac{d\phi}{dx} \rangle \\ &=& -\int_0^\infty\frac{d\phi}{dx}dx \\ &=& -[\phi(x)]_0^\infty \\ &=& \phi(0) \\ &=& \langle \delta, \phi \rangle \\ \end{matrix}$$

• 1行目が超関数の微分の定義
• 2行目は汎関数として対応する積分計算
• 3行目は積分を評価
• 4行目は$\phi(\infty)=0$であることを用いて展開
• 5行目はデルタ関数の定義より

以上よりReLUを超関数の意味で2回微分するとデルタ関数が出てくることが分かりました。

最後に $x+{\rm ReLU}(-x)$ の超関数としての微分がどうなるか愚直に確認してみましょう。

$$\begin{matrix} \langle \frac{dT_{x+{\rm ReLU(-x)}}}{dx}, \phi \rangle &=& -\langle T_{x+{\rm ReLU(-x)}}, \frac{d\phi}{dx} \rangle \\ &=& -\int_{-\infty}^\infty (x+{\rm ReLU(-x)})\frac{d\phi}{dx}dx \\ &=& -\int_0^\infty x\frac{d\phi}{dx}dx \\ &=& -[x\phi(x)]_0^\infty + \int_0^\infty \phi(x)dx \\ &=& \int_0^\infty \phi(x)dx \\ &=& \langle H, \phi \rangle \\ \end{matrix}$$

3行目以降は通常のReLUの微分と同じ流れになっており、結果が一致する ことが分かります。実は超関数は汎関数になっているので"原点における値"というものが意味を持つとは限らず、値を評価するためには常にテスト関数で評価する必要があります。超関数ではこのようにして1点での評価を回避することで、通常の意味では微分を定義できない関数の微分を定義できる ようになっているのです。

$\lambda_\delta$

"Distribution Theoretic Semantics for Non-Smooth Differentiable Programming" で提案されている $\lambda_\delta$ という計算体系は単純型付きラムダ計算を拡張したものになっており、以下のような型を持ちます。

$$\begin{matrix} \tau &:=& {\mathbb R} \\ &|& {\mathbb R}^+ \\ &|& {\rm Pred}({\mathbb R}^n) \\ &|& {\mathbb N} \\ &|& \tau \times \tau \\ &|& {\mathcal D}'({\mathbb R}^n) \\ &|& {\mathcal D}({\mathbb R}^n) \\ &|& \tau \rightarrow \tau \\ \end{matrix}$$

上から順番に

• 実数
• 正の実数
• ${\mathbb R}^n$ を引数に取る述語
• 自然数
• 直積
• ${\mathbb R}^n$ 上の超関数の集合
• ${\mathbb R}^n$ 上のテスト関数の集合
• 関数

を表しています（正確にはまだ意味論を考えているわけではないので上記はあくまでお気持ちです）。${\mathbb R}^n$ は ${\mathbb R} \underset{n}{\times \dots \times} {\mathbb R}$ の糖衣構文です。

ところで ${\rm Pred}({\mathbb R}^n)$ は少し構造を持ちすぎており、真偽値を表す型 ${\mathbb B}$ があれば ${\mathbb R}^n \rightarrow {\mathbb B}$ として述語を表現できるのではと思われるかもしれません。しかしこのやり方だと後で意味論を考える際に滑らかな関数のみを対象とするため ${\mathbb R}^n \rightarrow {\mathbb B}$ に属する値（関数）は少なくとも連続である必要があり常に真を返す関数 or 常に偽を返す関数しか表現できなくなってしまうという問題があります。これを回避するために滑らかな述語を表す ${\rm Pred}({\mathbb R}^n)$ を直接用意しているのです。

$\lambda_\delta$ をHaskellで実装するため型を表すデータ構造を実装しておきましょう。

data DType = R
           | Rp
           | Pred Int
           | N
           | Prod DType DType
           | D' Int
           | D Int
           | F DType DType
           deriving (Show, Eq)

次に $\lambda_\delta$ の項を見てみましょう。

$$\begin{matrix} t, u &:=& x \\ &|& r \\ &|& (t, u) \\ &|& {\rm let}\ (x, y) = t\ {\rm in}\ u \\ &|& {\rm let}\ x = t\ {\rm in}\ u \\ &|& \lambda x : \tau . t \\ &|& t\ u \\ &|& {\rm lift}(t) \\ &|& {\mathbb I}_t(u) \\ &|& \frac{\partial t}{\partial x} \\ &|& t +. u \\ &|& t *. u \\ &|& \langle t, u \rangle \\ &|& \phi^n(c, r) \\ &|& \delta_t \\ &|& {\rm it}\ t\ u \\ &|& {\rm arithmetic} \\ &|& {\rm comparators} \\ \end{matrix}$$

上から順番に

• 変数
• スカラー（実数）
• タプル
• let記法によるタプルの分解
• let記法
• ラムダ抽象
• 関数適用
• 超関数への持ち上げ
• 指示関数
• 微分
• 超関数同士の和
• スカラーと超関数の積
• 超関数へのテスト関数の適用
• 中心c半径rを持つn次元の隆起関数
• デルタ関数
• 関数の反復適用
• （実数や自然数の基本的な算術）
• （実数や自然数の基本的な比較演算）

を表しています（正確にはまだ意味論を考えているわけではないので上記はあくまでお気持ちです）。指示関数は本当は白抜きの$1$で表したかったのですがZennが数式をレンダリングするために使っているKaTeXが白抜きの数字をまだサポートしていないため${\mathbb I}$で代用しています。

中心c半径rを持つ隆起関数は以下のような式で表される関数です。

$$\phi_r^c(x) = \begin{cases} \exp\left(-\frac{1}{1-\left(\frac{x-c}{r}\right)^2}\right) && \ \ |x-c| < r\\ 0 && \ \ {\rm otherwise} \\ \end{cases}$$

これは中心c半径rの超球をコンパクトなサポートに持つ滑らかな関数となっており、テスト関数として使われます。

項を表すデータ構造も実装しておきましょう。

type Name = String

newtype Predicate a = Predicate (a -> Bool)

instance Show (Predicate a) where
  show (Predicate _) = "p"

data DTerm = Variable Name
           | Scalar Double
           | P Int (Predicate [Double])
           | Tuple DTerm DTerm
           | LetPair Name Name DTerm DTerm
           | Let Name DTerm DTerm
           | Lambda Name DType DTerm
           | Apply DTerm DTerm
           | Lift DTerm
           | Ind DTerm DTerm
           | Der Name DTerm
           | Add DTerm DTerm
           | SMul DTerm DTerm
           | DApply DTerm DTerm
           | Bump DTerm Double
           | Delta DTerm
           | Iterate DTerm DTerm
           deriving (Show)

実装した際に ${\rm Pred}({\mathbb R}^n)$ に型付けられるプリミティブを表す項が必要なことに気づいたので P Int (Predicate [Double]) を足しています。算術と比較演算の実装は省略しています。

DTerm は直和成分が多いので Show のインスタンスを deriving で自動的に実装したかったのですが、述語の部分だけが関数を含むので単純には出来ませんでした。そのため述語を表す関数を Predicate として新しいデータ型として定義し Show のインスタンスを定義することで DTerm で Show を deriving 出来るようにしています（derivingするためだけに型のネストを1つ増やすのは、このあとの実装で変換コストが毎回かかることを考えると少し微妙ですね…）。

型と項を確認したので、次は $\lambda_\delta$ の型付け規則を見てみましょう。

こちらは原論文に記載されている型付け規則の図です。これらの規則を元に項に型付けを行うプログラムを実装してみましょう。

import Data.List

type Context = [(Name, DType)]

dim :: DType -> Either String Int
dim R = Right 1
dim (Prod R t) = fmap (+ 1) (dim t)
dim x = Left $ concat [show x, " has no dimension."]

typeof :: Context -> DTerm -> Either String DType
typeof ctx (Variable x) =
  case lookup x ctx of
    Just t -> Right t
    Nothing -> Left $ concat ["Variable ", x, " is not found."]
typeof ctx (Scalar _) = Right R
typeof ctx (P n p) = Right $ Pred n
typeof ctx (Tuple t u) = do
  t1 <- typeof ctx t
  t2 <- typeof ctx u
  pure $ Prod t1 t2
typeof ctx (Let x term u) = do
  t <- typeof ctx term
  typeof ((x, t) : ctx) u
typeof ctx (LetPair x y (Tuple term1 term2) u) = do
  t1 <- typeof ctx term1
  t2 <- typeof ctx term2
  typeof ((x, t1) : (y, t2) : ctx) u
typeof ctx (LetPair x y t u) = Left $ concat ["Invalid let pair: ", show (LetPair x y t u)]
typeof ctx (Lambda x t1 term) = do
  t2 <- typeof ((x, t1) : ctx) term
  pure $ F t1 t2
typeof ctx (Apply term1 term2) = do
  (t1, t2) <- case typeof ctx term1 of
    Right (F t1 t2) -> Right (t1, t2)
    Right _ -> failure
    Left msg -> Left msg
  t3 <- typeof ctx term2
  if t1 == t3 then Right t2 else failure
  where
    failure = Left $ concat ["Invalid application: ", show (Apply term1 term2)]
typeof ctx (Lift term) = do
  t1 <- case typeof ctx term of
    Right (F t1 R) -> Right t1
    Right _ -> Left $ concat ["Only function types can be lifted.", show (Lift term)]
    Left msg -> Left msg
  D' <$> dim t1
typeof ctx (Ind t1 t2) = do
  n <- case typeof ctx t1 of
    Right (Pred n) -> Right n
    Right _ -> failure
    Left msg -> Left msg
  t <- case typeof ctx t2 of
    Right (F t R) -> Right t
    Right _ -> failure
    Left msg -> Left msg
  m <- dim t
  if n == m then Right (D' n) else failure
  where
    failure = Left (concat ["Invalid indicator: ", show (Ind t1 t2)])
typeof ctx (Der x t) =
  case typeof ctx t of
    Right (D' n) -> Right (D' n)
    Right _ -> Left $ concat ["Invalid derivative: ", show (Der x t)]
    Left msg -> Left msg
typeof ctx (Add t1 t2) = do
  n1 <- case typeof ctx t1 of
    Right (D' n) -> Right n
    Right _ -> failure
    Left msg -> Left msg
  n2 <- case typeof ctx t2 of
    Right (D' n) -> Right n
    Right _ -> failure
    Left msg -> Left msg
  if n1 == n2 then Right (D' n1) else failure
  where
    failure = Left $ concat ["Invalid distribution addition: ", show (Add t1 t2)]
typeof ctx (SMul t1 t2)
  | typeof ctx t1 == Right R =
    D'
      <$> case typeof ctx t2 of
        Right (D' n) -> Right n
        Right _ -> failure
        Left msg -> Left msg
  | otherwise = failure
  where
    failure = Left $ concat ["Invalid scalar multiplication: ", show (SMul t1 t2)]
typeof ctx (DApply t1 t2) = do
  n1 <- case typeof ctx t1 of
    Right (D' n) -> Right n
    Right _ -> failure
    Left msg -> Left msg
  n2 <- case typeof ctx t2 of
    Right (D n) -> Right n
    Right _ -> failure
    Left msg -> Left msg
  if n1 == n2 then Right R else failure
  where
    failure = Left $ concat ["Invalid distribution application: ", show (DApply t1 t2)]
typeof ctx (Bump term _) = do
  t <- typeof ctx term
  D <$> dim t
typeof ctx (Delta term) = do
  t <- typeof ctx term
  D' <$> dim t
typeof ctx (Iterate term1 term2) = do
  t <- typeof ctx term1
  (t1, t2) <- case typeof ctx term2 of
    Right (F t1 t2) -> Right (t1, t2)
    Right _ -> failure
    Left msg -> Left msg
  if t == t1 && t == t2 then Right (F N t) else failure
  where
    failure = Left $ concat ["Invalid iteration: ", show (Iterate term1 term2)]

Eitherモナドでエラーハンドリングをしながら規則を一つ一つ愚直に実装しています。

実装した型付けのプログラムを用いてReLUに相当する $\lambda_\delta$ の項に正しく型が付くか確認してみましょう。

relu :: DTerm
relu = Ind (P 1 (Predicate $ \[x] -> x >= 0.0)) (Lambda "x" R (Variable "x"))

> typeof [] relu
Right (D' 1)

無事、実数上の超関数と型付けられていますね👏

以上のソースコードはRepl.it上で公開しているので興味のある人は動かして遊んでみてください。

意味論とそれから

$\lambda_\delta$ の項として実装した relu を実際に動かすには、記号列としての項から動かすことが出来る対象への変換、すなわち意味論を考える必要があります。今は微分可能プログラミングを考えているので変換先の対象としては、例えば滑らかな多様体と滑らかな写像の圏${\rm Man}$が考えられるでしょう。しかし実は${\rm Man}$はデカルト閉にはならず冪対象が存在するとは限りません（すなわち滑らかな多様体から滑らかな多様体への滑らかな写像全体が再び滑らかな多様体になるとは限りません）。そのため関数を対象として扱うような高階関数を取り扱うことが難しくなるという問題があります。この問題を回避するために滑らかな空間を更に一般化した Diffeological space の圏 ${\rm Diff}$ というものを考えます。${\rm Diff}$ についてはここでは詳しく述べませんが、原論文では $\lambda_\delta$ の項を ${\rm Diff}$ の対象に変換することで意味論を与えています。

• diffeological space in nLab

さて、本当であればここからHaskellを使って relu を適当な関数に変換して実際に動かしてみる、さらにはニューラルネットワークを実装して動かしてみるということをしようと思っていたのですが、ここまで書いてからこの展開にはいくつか問題があることに気が付きました。

まず relu 及びそれによって実装したニューラルネットワークを変換した先の対象は超関数 ${\mathcal D}'({\mathbb R})$ の元となるはずですが、一般的に超関数は具体的な点における値というものを定義することが出来ません。この問題については原論文でも Remark A.7. で触れられており、点ではなく評価する点を中心とする半径の小さな隆起関数を使って評価することで解決できる（半径を小さくすれば任意の精度で近似できる）とされています。ただMNISTのような基本的な課題を解くプログラムでも入力次元分の784個の隆起関数を用意して評価する（評価には数値積分が伴う）と考えると実際に実装して動かすのは精度や速度の観点から難しそうです。

もう一つの問題は一般的には超関数の関数合成が定義できないということです。単純な3層ニューラルネットワークを実装することを考えてもReLUによる変換を伴う層を2つ用意して合成する必要がありますが、用意した層はそれぞれが超関数になっており、超関数同士の関数合成が定義されていないため素直に合成することが出来ません。そのため合成を行う前に隆起関数を用いて毎回実数に評価し、再び隆起関数に変換して次の層に入力する必要があります。これは流石に手間ですね。

もちろんこれらの問題は形式的な議論のために作られた言語体系を使って無理やり実践的な問題を解いてみようとしたから起こったことなので（私が勝手にやったことです）、 $\lambda_\delta$ 自体に問題があるわけではありません。将来的にはこの様な理論と実践のギャップが埋まっていくような方向にも研究が進んでいくと嬉しいですね。

脚注

1. 宣伝『確率とモナドと確率的プログラミング』

2. 宣伝『教師あり学習の学習モデルを微分可能プログラミングと純粋関数型言語で記述する』

3. このような例は他にもあり、例えば arXiv:2006.02080 で言及されています

4. そういえば最近、重みを決定的に0と1（定数倍を除く）で初期化するZerO Initializationという手法も提案されてましたね arXiv:2110.12661