👷

型安全で高速な連鎖行列積の計算

2021/12/22に公開

Haskell

この記事は Haskell Advent Calendar 2021 の22日目の記事です。

次のような３つの行列の積を考えてみましょう。

ABC = \begin{pmatrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \\ a_{20} & a_{21} & a_{22} \\ a_{30} & a_{31} & a_{32} \\ \end{pmatrix} \begin{pmatrix} b_{00} & b_{01} \\ b_{10} & b_{11} \\ b_{20} & b_{21} \\ \end{pmatrix} \begin{pmatrix} c_{00} & c_{01} & c_{02} & c_{03} & c_{04} \\ c_{10} & c_{11} & c_{12} & c_{13} & c_{14} \\ \end{pmatrix}

行列積は結合律が成り立つので $AB$ を先に掛け算しても $BC$ を先に掛け算しても結果は一致します。

(AB)C = A(BC)

しかし計算に必要は演算の回数はどうでしょうか。まず $AB$ を先に掛け算した場合、 $4\times 3$ 行列と $3\times 2$ 行列の積になるので $3$ 次元ベクトルの内積を $4\times 2 = 8$ 回繰り返すことになります。特に要素の積に注目すると $3\times 4\times 2=24$ 回の積が行われます。一般に $p\times q$ 行列と $q\times r$ 行列の行列積では $pqr$ 回の要素の積と $p(q-1)r$ 回の要素の和を計算する必要があり、演算を実行する回数のオーダーは $O(pqr)$ であることが分かります。その後 $4\times 2$ 行列 $AB$ と $2\times 5$ 行列 $C$ の積を行い、演算は $2\times 4\times 5= 40$ 回行われることになります。すなわち行列積 $(AB)C$ における演算は合計 $24+40=64$ 回行われることになります。

反対に $BC$ を先に掛け算した場合、同様の考え方により $A(BC)$ の計算に $2\times 3\times 5 + 3\times 4\times 5 = 90$ 回の演算が必要になることが分かります。つまり行列積はどこから計算しても答えは同じになりますが計算にかかるコストは計算する順番によって変わってくるのです。

計算する順番は与えられた行列積にどのような括弧つけるのかに対応しています。括弧を付ける組み合わせの数は3つの行列の積では2通りしかありませんでしたが、掛け合わせる行列の数が増えるにつれて指数関数的に増加していきます。なので全ての組み合わせを列挙して行列積のコストが一番低いパターンを探索するのは困難です。しかし $n$ を掛け合わせる行列の個数とした時、実は最適な計算順序は動的計画法を使うことで $O(n^2)$ で求まることが知られています^[1]。このように複数の行列が与えられた時、それらの積を行う最小コストを求める問題は連鎖行列積問題と呼ばれています。

ところでHaskellではベクトルや行列の型にそれらの次元に関する情報を持たせるができます。そこで行列積を行う行列の組み合わせが与えられた時に、型にある次元の情報から最適な行列積を行う順番を自動的に計算しその通りに行列積を実行するような関数を実装することはできないでしょうか。

行列と連鎖行列の型

この記事では線形代数ライブラリとしてhmatrixのNumeric.LinearAlgebra.Staticを用います。このライブラリで $m\times n$ 行列の型は

data L m n = ...

と定義されています。

行列積を行う対象となる複数の行列の組、すなわち連鎖行列を表す型を考えてみましょう。最も簡単に思いつくのは行列の単純なリストとして表現することでしょう。

type MCList m n = [L m n]

ここでMCListはMatrix Chain Listの意味です。しかしこれはうまくいきません。なぜならこの型ではリストの要素は全て $m\times n$ 行列となってしまいますが、実際の行列積は $m\times k$ 行列と $k\times n$ 行列の積など様々な型の行列の積を考えなければいけないからです。

そこでGADTを用いて独自のデータ型を作ってみましょう^[2]。

data MCList m n where
  S :: L m n -> MCList m n
  (:.) :: KnownNat k => L m k -> MCList k n -> MCList m n

infixr 5 :.

このMCList m nは行列積を行なった結果が $m\times n$ 行列となるような連鎖行列を表す型です。Sは行列を1つ取ってMCListを構築する値コンストラクタであり、(:.)は計算結果が $k\times n$ 行列となる連鎖行列の型の先頭に $m\times k$ 行列を追加する値コンストラクタです。(:.)は中間にある次元kを存在型で隠蔽してしまうので結果の型MCList m nにkが現れることはありません。中間にある次元を明示的に管理しないことでコードが煩雑になることを防いでいます。ただし単なる存在型だと後の実装で扱いに困ってしまうのでKnownNatのインスタンスであるという制約だけつけています。

このMCListを使って単純に右から順番に行列積を計算する関数を作ってみましょう。

naiveMcm :: (KnownNat m, KnownNat n) => MCList m n -> L m n
naiveMcm (S a)    = a
naiveMcm (a :. b) = a <> naiveMcm b

(<>)はhmatrixが提供する行列積を行う演算子です。この演算子は

(<>) :: L m k -> L k n -> L m n

という型をしていて、掛け合わせる行列の次元が正しく揃っていないとコンパイルができないようになっています。naiveMcmの実装ではGADTのパターンマッチが行われることで行列aの列の次元と連鎖行列bの行の次元が一致することが保証されるので上記のコードは問題なくコンパイルすることができるのです。

型の情報から連鎖行列問題を解く

連鎖行列問題を解くために、まずは連鎖行列の型から行列の次元をリストとして取り出す関数を実装してみましょう。

num :: forall n a. (KnownNat n, Num a) => a
num = fromIntegral $ natVal (Proxy @n)

dims :: forall m n. (KnownNat m, KnownNat n) => MCList m n -> [Int]
dims (S a)      = [num @m, num @n]
dims (_ :. mcm) = num @m : dims mcm

numはTypeApplicationsを利用して型レベルの自然数から値を取り出すための補助関数です。dimsはMCListを再帰的に辿って行列の次元のリストを作る関数です。例えば $p\times q$ 行列と $q\times r$ 行列という2つの行列の積をdimsに与えると[p, q, r]というリストが返ってきます。このリストの長さは与えた連鎖行列に含まれる行列の数より1つ長くなっていることに注意してください。

いよいよ動的計画法を使って行列積の最小コストを求めてみましょう。ただしよくある競技プログラミングの問題とは違って今回は最終的に行列積自体を計算することが目的です。なので最小コストを求めると同時にそれを達成する計算順序も求める必要があります。計算順序は二分木を使って表現することができます。このことは以下のようにイメージすると良いでしょう。

計算順序を表すデータ型として形状の情報のみを持つ二分木の型を用意しておきます。

data Tree = Leaf | Node Tree Tree
          deriving (Eq, Ord)

動的計画法を実装する方針は、i番目の行列からj番目の行列までの積を求める最小コストをボトムアップに計算していくというものです。

iからj番目の行列積を考える時、間にあるk番目で区切った場合にかかる計算コストは、

iからk番目までの行列積の最小コスト
k+1からj番目までの行列積の最小コスト
i,k+1,j+1番目の次元の積

これらの和になります。最後でkとjに1が足されているのは次元のリストが積を行う数のリストより1つ長くなっていることに対応しています。

これをkをiからj-1まで順番に変化させて計算し、その中で一番小さいコストがiからj番目の行列積の最小コストになるというわけです。

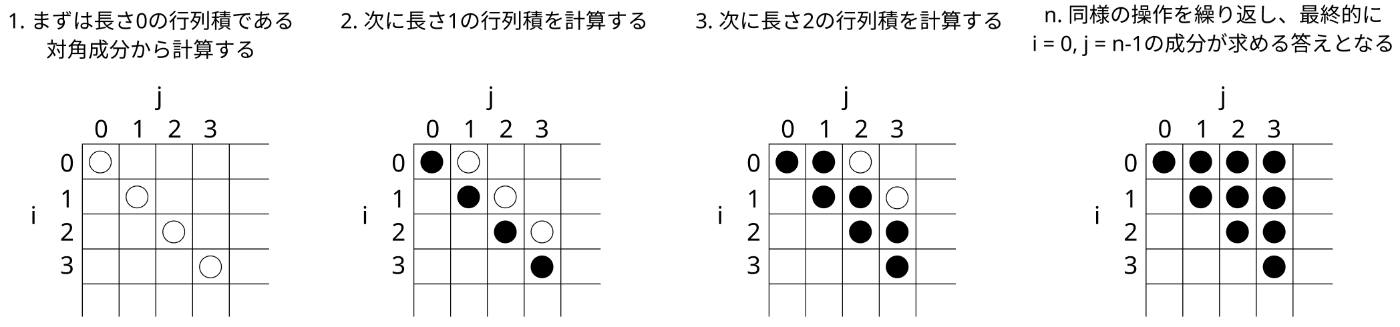
この計算を行なった値を保存するために2次元の配列を用意します。計算は積を行う行列の数が少ない方から、つまり2次元配列の対角線から順番に行なっていきます。

minCost :: (KnownNat m, KnownNat n) => MCList m n -> (Int, Tree)
minCost xs = runST $ do
  let ds = dims xs
      n = length ds - 1
      costs = listArray (0,n) ds :: UArray Int Int
      indices = [(x, x+offset) | offset <- [0..n-1], x <- [0..n-1-offset]]
  table <- newArray_ ((0,0), (n-1,n-1)) :: ST s (STArray s (Int, Int) (Int, Tree))
  for_ indices $ \(i,j) ->
    if i == j then writeArray table (i,j) (0, Leaf)
    else do
      candidates <- for [i..j-1] $ \k -> do
        (cik, tik) <- readArray table (i,k)
        (ckj, tkj) <- readArray table (k+1,j)
        pure (cik + ckj + costs!i * costs!(k+1) * costs!(j+1), Node tik tkj)
      writeArray table (i, j) $ minimum candidates
  readArray table (0, n-1)

このminCostを使えば行列積のコストが最小になる計算順序を求めることができます。

計算順序に沿って行列積を計算する

連鎖行列MCListとそれを最小コストで計算する計算順序Treeが手に入ったので、実際に計算順序に沿って行列積を計算する方法を考えてみましょう。そのためには単なるリストではなく計算順序も反映した連鎖行列の型を考えなければいけません。これを以下のような型を持った木として実装します。

data MCTree m n where
  L :: L m n -> MCTree m n
  N :: KnownNat k => MCTree m k -> MCTree k n -> MCTree m n

MCTree m nは計算結果が $m\times n$ 行列となるような連鎖行列を表す型です。この型を用いた連鎖行列積は以下のように実装することができます。

mcmTree :: (KnownNat m, KnownNat n) => MCTree m n -> L m n
mcmTree (L a) = a
mcmTree (N l r) = mcmTree l <> mcmTree r

木構造を用いることで計算順序が期待通りに反映されているのが分かります。

それでは最も重要なMCTreeの作り方について見ていきましょう。いきなり複雑な型で考えるのは難しいので、まずは普通のリストを普通の木に沿って木を組み立てる関数を考えてみます。

data Tree' a = Leaf' a
             | Node' (Tree' a) (Tree' a)

buildLT :: [a] -> Tree' () -> (Tree' a, [a])
buildLT (a:as) (Leaf' _) = (Leaf' a, as)
buildLT as (Node' l r) =
  let (l', as')  = buildLT as  l
      (r', rest) = buildLT as' r
   in (Node' l' r', rest)

buildLTはリスト[a]の要素を構造Tree' ()に沿って組み立てた木Tree' aを計算する関数です。返り値が組み立てた木Tree' aと余った要素のリスト[a]のタプルになっているので再帰的に木を組み立てていくことができます。buildLTの実装でNode'でパターンマッチされた部分を見てみると、まずNode'の左側の木lと与えられたリスト全体asで木の組み立てを行い、余った要素のリストas'を使って右側の木rで木の組み立てを行っているという処理の流れです。

同様の処理をMCListとMCTreeで行おうとすると1つ困ったことが起こります。木を組み立てる途中で連鎖行列を組み立た木と余りの要素のリストに分轄するのですが、この分割を行った際に境界にある次元が木とリストで一致していることを保証する必要が出てくるのです。これを解決するために以下のようなデータ型を新たに定義します。

data SomeTreeList m n where
  NoRest :: MCTree m n -> SomeTreeList m n
  SomeTreeList :: KnownNat k => (MCTree m k, MCList k n) -> SomeTreeList m n

NoRestは余りの要素のリストが空になった場合を表します。SomeTreeListは木とリストのペアになっていますが存在型によって間の次元kが一致していることを保証するようにできています。これを利用すればMCListとTreeから木を組み立てる関数は以下のように実装することができます。

buildMCTree :: (KnownNat m, KnownNat n) => MCList m n -> Tree -> SomeTreeList m n
buildMCTree (S a)    Leaf = NoRest (L a)
buildMCTree (a :. b) Leaf = SomeTreeList (L a, b)
buildMCTree as (Node l r) =
  case buildMCTree as l of
    (NoRest _) -> undefined
    (SomeTreeList (l', as')) ->
      case buildMCTree as' r of
        (NoRest r') -> NoRest (N l' r')
        (SomeTreeList (r', rest)) -> (SomeTreeList (N l' r', rest))

動作はbuildLTの場合とほぼ同じです。組み立た木を使って行列積を行う関数を実装してみましょう。

mcm :: (KnownNat m, KnownNat n) => MCList m n -> L m n
mcm xs =
  let (_, parenthesis) = minCost xs
   in case buildMCTree xs parenthesis of
        (NoRest tree) -> mcmTree tree
        (SomeTreeList (tree, _)) -> undefined

buildMCTreeとmcmにundefinedが現れる箇所が1つずつあります。これは与えられたMCListとTreeの長さが一致している保証が型レベルで与えられていないためで、それぞれ木が短かった場合と長すぎた場合に対応しています。さらに型レベルプログラミングを進めることでこのundefinedを無くせる可能性はありますが、今回は計算順序の木の構築はmcmの中で完結しており、木とリストの長さは必ず一致するので深くは追求しないことにします。

最後に、実装したmcmを使うことで実際に行列積の計算が速くなるのか確認してみましょう。

withTime :: IO a -> IO ()
withTime action = do
  start <- getCurrentTime
  action
  end <- getCurrentTime
  putStrLn $ formatTime defaultTimeLocale "Time: %-3Ess" (diffUTCTime end start)

main :: IO ()
main = do
  putStrLn "Generating random matrices"
  !a <- randn @100 @500
  !b <- randn @500 @1000
  !c <- randn @1000 @5000
  !d <- randn @5000 @10000
  let m = a :. b :. c :. S d

  putStrLn "# mcm"
  withTime . putStrLn $ "norm: " ++ show (norm_2 (mcm m))

  putStrLn "# naiveMcm"
  withTime . putStrLn $ "norm: " ++ show (norm_2 (naiveMcm m))

この例では $100\times 500$ 行列と $500\times 1000$ 行列と $1000\times 5000$ 行列と $5000\times 10000$ 行列という4つの行列の積を計算しています。naiveMcmにより右から計算すると計算コストは

100 \times 500 \times 10000 + 500 \times 1000 \times 10000 + 1000 \times 5000 \times 10000 = 555 \times 10^8

となりますが、mcmを用いて左から計算することで

100 \times 500 \times 1000 + 100 \times 1000 \times 5000 + 100 \times 5000 \times 10000 = 555 \times 10^7

となり計算コストをちょうど10分の1に減らすことができます。実行してみると、

Generating random matrices
# mcm
norm: 8072309.181602492
Time: 0.474s
# naiveMcm
norm: 8072309.181602493
Time: 3.209s

となり、もちろん順序計算などのオーバーヘッドがあるため10分の1にはなりませんが、かなり高速に計算できるようになりました👏

今回実装したコードはこちらのgistにアップロードしています。

＼読んでいただきありがとうございました！／
この記事が面白かったらいいね♡ をいただけると嬉しいです☺️
バッジを贈っていただければ次の記事を書くため励みになります🙌

脚注

この問題は更に効率的に解くことができ $O(n\log n)$ で解けることが知られています https://en.wikipedia.org/wiki/Matrix_chain_multiplication#More_efficient_algorithms ↩︎
今回はGADTを使いましたがヘテロリストとsingletonsを使った実装も可能です（少々煩雑にはなりますが） ↩︎

行列と連鎖行列の型

型の情報から連鎖行列問題を解く

計算順序に沿って行列積を計算する

Discussion