🥑
代数的データ型と Combinatorial Species

2024/12/09に公開
これは「Haskell Advent Calendar 2024」9日目の記事です。
代数的データ型は簡潔性を保ちながら型安全で表現力豊かなプログラムを記述するため欠かせない存在です。代数的データ型の原型は1966年にLandinが提案したISWIMに見られます。その後、1977年にNPLという関数型プログラミング言語に実装され、Standard MLやMiranda、Haskellに実装されていきました[1]。Haskellにおいて代数的データ型は型の 直和 と 直積 が表現でき、再帰的な定義 （再帰データ型）も可能です。
-- 直和型（Either a b と等価）
data Sum a b = A a | B b

-- 直積型（タプル (a, b) と等価）
data Product a b = Product a b

-- 再帰データ型の例
data List a = Nil | Cons a (List a)
この直和と直積という演算を持っていることが代数的データ型が "代数的" と呼ばれる所以ですが、これらの操作が本当に和と積に対応していることを直感的に理解することは可能でしょうか？例えばryota-ka氏の『代数的データ型と初等代数学』では基本的な代数的データ型に 0,1,2…0, 1, 2 \dots0,1,2… という名前をつけることで直和や直積といった操作がこれらの名前から連想される 自然数の代数的な演算が満たす性質と一致すること を説明しています。またBurget氏の "The algebra (and calculus!) of algebraic data types" では集合と対応付くような型を用いて[2]その値の数を数えることにより 「型の直和と直積」と「集合の直和と直積」の一致 を見ることで、代数的な振る舞いの直感的な解説を試みています。これらの対応を表にまとめてみましょう。


型
集合
要素の数


data Void
∅\emptyset∅
000

data One = One
{∗}\{*\}{∗}
111

type Two = Sum One One
{∗}+{∗}\{*\}+\{*\}{∗}+{∗}
1+1=21+1=21+1=2

data Maybe a = Nothing | Just a
{∗}+A\{*\} + A{∗}+A
1+∣A∣1+|A|1+∣A∣

data Sum a b = A a | B b
A⊔BA \sqcup BA⊔B
∣A∣+∣B∣|A|+|B|∣A∣+∣B∣

data Product a b = Product a b
A×BA \times BA×B
∣A∣×∣B∣|A|\times|B|∣A∣×∣B∣

a -> b
BAB^ABA
∣B∣∣A∣|B|^{|A|}∣B∣∣A∣

（ここで ⊔\sqcup⊔ は2つの集合の非交和を表す）
本稿ではこの
型から
集合に対応付け
要素の数を数える
という翻訳の流れを参考に、集合ではなく Combinatorial Species という概念を考えることで、代数的データ型に対するまた別の見方ができることを紹介したいと思います。

 Combinatorial Species有限集合を対象とし全単射を射とするような圏B{\mathcal B}Bの自己関手FFFを Combinatorial Species と呼びます。
F:B→B
F: {\mathcal B} \to {\mathcal B}
F:B→B例えば集合にその部分集合族を対応させるような関手は Combinatorial Species の例です。他にも集合にその要素を頂点とするグラフ全ての集合を対応させる関手や集合にその要素をノードとする木構造全ての集合を対応させる関手も Combinatorial Species と考えることができます。
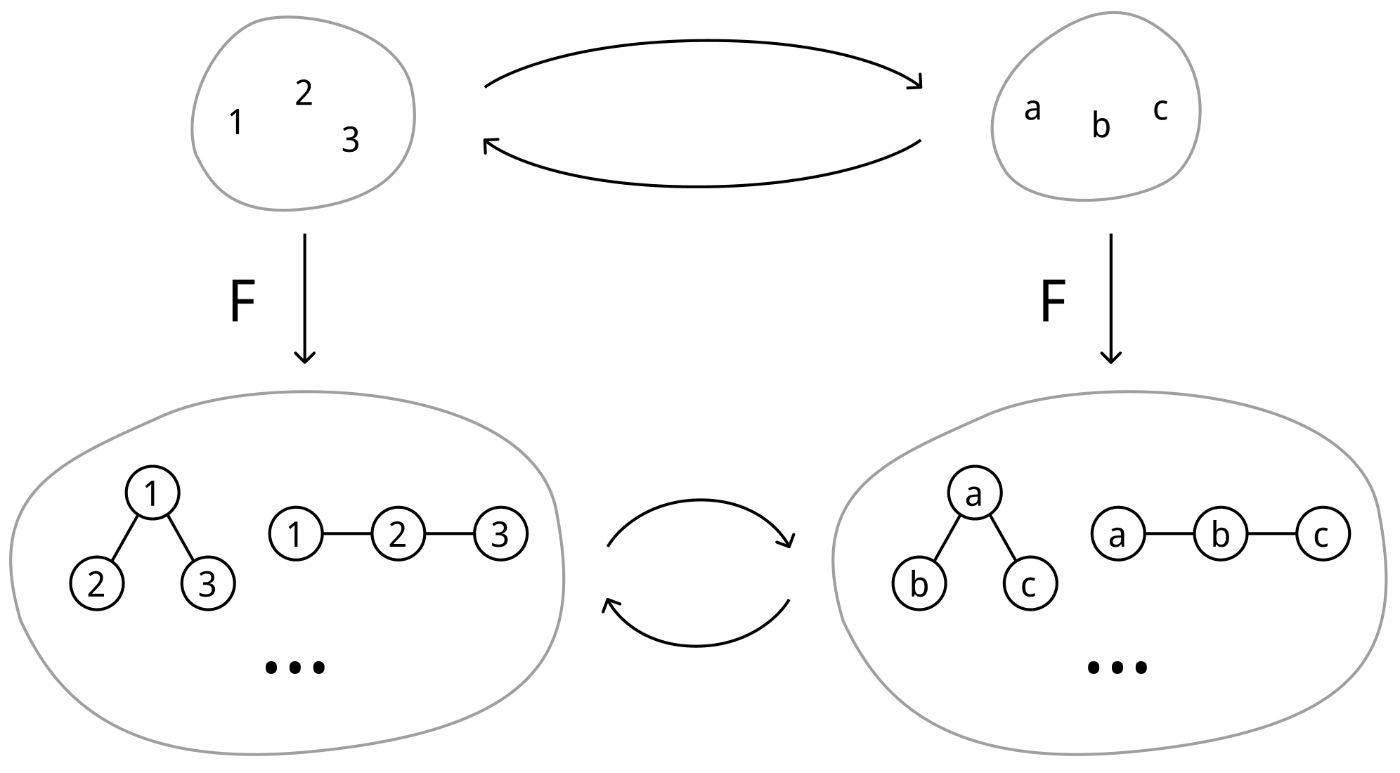
Combinatorial Species FFF は元の集合をラベルとして ラベルを何らかの構造に対応付けるもの であり、圏 B{\mathcal B}B の射が全単射であることは ラベルを取り換えても構造自体は変わらない ことを表していると解釈すると分かりやすいでしょう。
Combinatorial Species FFF に対しては以下のような多項式
F(x)=∑n≥0fnxnn!
F(x) = \sum_{n\geq 0}f_n\frac{x^n}{n!}
F(x)=n≥0∑​fn​n!xn​を対応付けることができ、この多項式は 母関数（指数型母関数） と呼ばれます。ここで fnf_nfn​ は nnn 個の要素を持つ集合 AAA に対する FAFAFA の要素の数 ∣FA∣|FA|∣FA∣ であり、圏 B{\mathcal B}B の射が全単射であることから fnf_nfn​ は集合 AAA の選択に依らず well-defined であることが分かります。
例えば nnn 点集合 AAA の部分集合は 2n2^n2n 個存在するので、集合にその部分集合族を対応させる Combinatorial Species FFF の母関数は
F(x)=∑n≥02nxnn!=∑n≥0(2x)nn!=exp⁡(2x)
F(x) = \sum_{n\geq 0}2^n\frac{x^n}{n!} = \sum_{n\geq 0}\frac{(2x)^n}{n!} = \exp(2x)
F(x)=n≥0∑​2nn!xn​=n≥0∑​n!(2x)n​=exp(2x)となります。

 代数的データ型の翻訳Haskell の代数的データ型を Combinatorial Species に対応付ける 方法を考えてみましょう。Combinatorial Species は関手なので例えば次のような Functor にできる一般的な型を考えましょう。
data F a = A | B1 a | B2 a | C a a | D a a a
この型 F に対応する Combinatorial Species FFF として
空集合に対しては1点集合 AAA を対応させ
1点集合に対しては、その集合でラベル付けられた構造 B1,B2B_1, B_2B1​,B2​ を持つ2点集合を対応させ
2点集合に対しては、その集合でラベル付けられた構造 CCC を持つ2点集合を対応させ（構造は1つですがラベルの組み合わせが2通りあるので2点集合）
3点集合に対しては、その集合でラベル付けられた構造 DDD を持つ6点集合を対応させ（構造は1つですがラベルの組み合わせが6通りあるので6点集合）
それ以外の集合に対しては空集合を対応させる
ような関手を考えることとします。
この FFF の母関数は定義より
F(x)=1+2x+x2+x3
F(x) = 1 + 2x + x^2 + x^3
F(x)=1+2x+x2+x3となります。
なんとなく翻訳のルールは分かるかもしれませんが、議論を明確にするためにここからは基本的な型とそれに対応する Combinatorial Species を定義し、それらを代数的に組み合わせることでより複雑な対応をカノニカルに構築していく方法を考えたいと思います。

 Regular Speciesまず最も基本的な型は値コンストラクタを持たない型でしょう。
data Void a -- 実装は空
この型に対応する Combinatorial Species は 任意の集合を空集合に対応付ける関手 で、その母関数は
F(x)=0
F(x) = 0
F(x)=0となります。この Combinatorial Species を 000 と呼ぶことにしましょう。
次に基本的な型として以下のような1つの値コンストラクタを持つような型を考えます。
data One a = One
この型に対応する Combinatorial Species は 空集合を1点集合に対応付けそれ以外の集合を空集合に対応付ける関手 で、その母関数は
F(x)=1
F(x) = 1
F(x)=1となります。この Combinatorial Species を 111 と呼ぶことにしましょう。
Combinatorial Speceis との対応を考えるためにここでの代数的データ型は型変数 a を取る形になっていましたが、型 Void a と One a における a は幽霊型であり Void a は Data.Void の Void, One a はUnit型 () に同型です。ですので型変数がない代数的データ型についても Void a,  One a と同型な型の組み合わせと考えることにより Combinatorial Species との対応を考えることができます。
最後に次のような型を考えます。
data X a = X a
この型に対応する Combinatorial Species は 1点集合を1点集合に対応付けそれ以外の集合を空集合に対応付ける関手 で、その母関数は
F(x)=x
F(x) = x
F(x)=xとなります。この Combinatorial Species を XXX と呼ぶことにしましょう。
ここからは代数的データ型の直和と直積に対応する Combinatorial Speceis の演算を考えます。
まずは以下のような 代数的データ型 f と g の直和 を表す型を考えます。
data Sum f g a = Inl (f a) | Inr (g a)
Sum f g a に対応する Combinatorial Speceis は、 f と g に対応する Combinatorial Speceis の直和です。Combinatorial Speceis FFF と GGG の直和 F+GF + GF+G は対象を
(F+G)A=FA⊔GA
(F+G)A = FA \sqcup GA
(F+G)A=FA⊔GAに写すような関手です（射の対応についても素直に定義します）。定義より F+GF + GF+G の母関数は元の Combinatorial Species の母関数の和となります。
(F+G)(x)=F(x)+G(x)
(F + G)(x) = F(x) + G(x)
(F+G)(x)=F(x)+G(x)次に以下のような 代数的データ型 f と g の直積 を表す型を考えます。
data Product f g a = Product (f a) (g a)
Product f g a に対応する Combinatorial Speceis は、 f と g に対応する Combinatorial Speceis の 種積 (Species Product) と呼ばれる掛け算です。Combinatorial Speceis FFF と GGG の種積 F∙GF \bullet GF∙G は対象を
(F∙G)A=∑A=U1⊔U2FU1×GU2
(F\bullet G)A = \sum_{A=U_1\sqcup U_2} FU_1 \times GU_2
(F∙G)A=A=U1​⊔U2​∑​FU1​×GU2​と写すもので、和は集合 AAA を表す非交和な分割全てに渡って取ることとします。（×\times× という記号はまた別の概念である Combinatorial Species のデカルト積に使用されるので種積は ∙\bullet∙ で表しています。）この種積 F∙GF\bullet GF∙G の母関数は元の母関数の積に対応します。
(F∙G)(x)=F(x)G(x)
(F \bullet G)(x) = F(x)G(x)
(F∙G)(x)=F(x)G(x)ここで一旦これまでに定義した Combinatorial Species 0,1,X0, 1, X0,1,X とその演算 +,∙+, \bullet+,∙ を用いて、いくつかの例を見てみましょう。
まず
type Two a = Sum One One a
という型を考えましょう。この型は以下のように Bool と同型であることが分かります。
twoToBool :: Two a -> Bool
twoToBool (Inl One) = False
twoToBool (Inr One) = True

boolToTwo :: Bool -> Two a
boolToTwo False = Inl One
boolToTwo True  = Inr One
Two a は2つの One a の直和なので対応する Combinatorial Species 1+11+11+1 の母関数は
(1+1)(x)=1+1=2
(1+1)(x) = 1+1 = 2
(1+1)(x)=1+1=2となります。この Combinatorial Species 1+11+11+1 を 222 と呼びましょう。nnn も同様に定義します。ここで定義した Combinatorial Species 0,1,2…0, 1, 2 \dots0,1,2… は種積についても自然に振る舞うことが分かります。例えば 2∙3=62\bullet 3 = 62∙3=6 になります。
次に
type Succ a = Sum One X a
という型を考えましょう。この型は以下のように Maybe a と同型であることが分かります。
succToMaybe :: Succ a -> Maybe a
succToMaybe (Inl One)   = Nothing
succToMaybe (Inr (X a)) = Just a

maybeToSucc :: Maybe a -> Succ a
maybeToSucc Nothing  = Inl One
maybeToSucc (Just a) = Inr (X a)
Succ a に対応する Combinatorial Species は 1+X1+X1+X であり、その母関数は
(1+X)(x)=1+x
(1+X)(x) = 1 + x
(1+X)(x)=1+xです。
ここで Combinatorial Species F,GF, GF,G の 合成 F∘GF\circ GF∘G という演算を考えましょう。Combinatorial Species は圏 B{\mathcal B}B の自己関手なのでまず合成としては単純に関手の合成が考えられます。しかし Combinatorial Species がラベルから構造への対応付けであるという描像を考えると単純に関手として合成した Combinatorial Species はラベルから対応付けられた構造の集合を更にラベルとして構造に対応付けられたものとなり最初のラベル自体が複製されてしまって（あるいは共有されてしまって）素直なイメージとは少し異なるものになってしまいます（ただしこれはこれで Combinatorial Species 同士の演算として考えることも可能です）。そこで Combinatorial Species の合成 F∘GF\circ GF∘G として、まず対象Aの非交和による分割 A=U1⊔U2⊔⋯⊔UkA = U_1 \sqcup U_2 \sqcup \dots \sqcup U_kA=U1​⊔U2​⊔⋯⊔Uk​ を考えそれぞれを GGG で写し、そのようにしてできた集合 {GU1,GU2,…,GUk}\{GU_1, GU_2, \dots, GU_k\}{GU1​,GU2​,…,GUk​} をさらにFで写したものを考えます。イメージとしては 最初にラベルをいくつかのグループに分けそれぞれのグループで構造 GGG に対応付けた後にそれらを更に構造 FFF に入れ子のように対応させたもの になります。これを式で書くと
(F∘G)A=∑π∈P(A)(Fπ×∏B∈πGB)
(F\circ G)A = \sum_{\pi\in P(A)}\left(F\pi\times\prod_{B\in\pi}GB\right)
(F∘G)A=π∈P(A)∑​(Fπ×B∈π∏​GB)となります。ここで P(A)P(A)P(A) は AAA の非交和による分割全ての集合を表します。F∘GF\circ GF∘G の母関数は FFF と GGG の母関数の合成関数になります。
(F∘G)(x)=F(G(x))
(F\circ G)(x) = F(G(x))
(F∘G)(x)=F(G(x))Haskellの型としても以下のような合成を対応付けます。
data Compose f g a = Compose (f (g a))
これを使って Compose Succ Two a という型を考えると、この型は Maybe Bool に同型であり、対応する Combinatorial Species は 1+2=31+2 = 31+2=3 であり、母関数も同様に 1+x1+x1+x の xxx に 222 を代入して 333 になることが分かります。
他にも種積の例として Product Two X a に対応する Combinatorial Species は 2∙X2\bullet X2∙X であり、その母関数は 2x2x2x となり、Product X X a に対応する Combinatorial Species は X∙XX\bullet XX∙X であり、その母関数は x2x^2x2 となります。これらの例から自然数を係数とする任意の有限次数多項式を母関数とする Combinatorial Species に対応する代数的データ型が構成できることが分かるでしょう。
ところでHaskellの代数的データ型では再帰的な定義が可能でした。例えば標準的なリストの型
data List a = Nil | Cons a (List a)
に対応する Combinatorial Species を考えることはできるでしょうか？このような再帰データ型の定義は型の最小不動点を取る操作と考えることができます。
これまでの考え方に基づくとこの List a に対応する Combinatorial Species LLL は
L≃1+X∙L
L \simeq 1 + X \bullet L
L≃1+X∙Lという同型対応が成り立つはずです。実は Combinatorial Species には Implicit Species Theorem [3]という定理がありこのような式を満たす Combinatorial Species の存在が保証されています。この定理によって存在が保証される Combinatorial Species を データ型の最小不動点に対応する Combinatorial Species と考えることにしましょう。上記式から LLL の母関数は形式的に
L(x)=1+x+x2+⋯=11−x
L(x) = 1 + x + x^2 + \cdots = \frac{1}{1-x}
L(x)=1+x+x2+⋯=1−x1​と書けることが分かります。
以上における Combinatorial Species 1,X1, X1,X とその演算 +,∙+, \bullet+,∙ 及び最小不動点を取る操作によって構成される Combinatorial Species は Regular Species と呼ばれています[4]。

 代数的データ型の微分Combinatorial Species には 微分 という操作を考えることができます。Combinatorial Species FFF の微分 F′F'F′ もまた Combinatorial Species であり、以下のように定義されます。
F′A=F(A⊔{∗})
F'A = F(A\sqcup\{*\})
F′A=F(A⊔{∗})つまり F′AF'AF′A は元の Combinatorial Species FFF に AAA と1点集合 {∗}\{*\}{∗} の非交和を適用したものと定義します。
いくつかの例を見てみましょう。
まず Combinatorial Species 000 は任意の集合を空集合に写すのでその微分も変わらず 000 になります。つまり
(0)′=0
(0)' = 0
(0)′=0です。
次に Combinatorial Species 111 は空集合のみ1点集合に対応しそれ以外は空集合に対応するため、微分が元の関手に引き数と1点集合との非交和を取ったものを適用する操作であることを考えると 111 の微分は任意の集合に空集合を対応付ける関手、つまり 000 となります。
(1)′=0
(1)' = 0
(1)′=0そして Combinatorial Species xxx は1点集合には1点集合を返しますがそれ以外は空集合を返すので、xxx の微分は空集合のみ1点集合に対応しそれ以外は空集合を返す関手、つまり 111 となります。
x′=1
x' = 1
x′=1今度は直和の微分を考えてみましょう。定義より
(F+G)′A=(F+G)(A⊔{∗})=F(A⊔{∗})⊔G(A⊔{∗})=F′A⊔G′A
\begin{matrix}
(F+G)'A
&=& (F+G)(A\sqcup\{*\}) \\
&=& F(A\sqcup\{*\})\sqcup G(A\sqcup\{*\}) \\
&=& F'A\sqcup G'A \\
\end{matrix}
(F+G)′A​===​(F+G)(A⊔{∗})F(A⊔{∗})⊔G(A⊔{∗})F′A⊔G′A​となるので Combinatorial Species F,GF, GF,G の直和 F+GF+GF+G の微分は F,GF, GF,G それぞれの微分の直和となります。
次に種積の微分は定義より
(F∙G)′A=(F∙G)(A⊔{∗})=∑A⊔{∗}=U1⊔U2FU1×GU2=∑A=U1⊔U2F(U1⊔{∗})×GU2+∑A=U1⊔U2FU1×G(U2⊔{∗})=∑A=U1⊔U2F′U1×GU2+∑A=U1⊔U2FU1×G′U2=(F′∙G)A+(F∙G′)A
\begin{matrix}
(F\bullet G)'A
&=& (F\bullet G)(A\sqcup\{*\}) \\
&=& \displaystyle\sum_{A\sqcup\{*\}=U_1\sqcup U_2} FU_1 \times GU_2 \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2} F(U_1\sqcup\{*\}) \times GU_2 + \displaystyle\sum_{A=U_1\sqcup U_2} FU_1 \times G(U_2\sqcup\{*\}) \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2} F'U_1 \times GU_2 + \displaystyle\sum_{A=U_1\sqcup U_2} FU_1 \times G'U_2 \\
&=& (F'\bullet G)A + (F\bullet G')A
\end{matrix}
(F∙G)′A​=====​(F∙G)(A⊔{∗})A⊔{∗}=U1​⊔U2​∑​FU1​×GU2​A=U1​⊔U2​∑​F(U1​⊔{∗})×GU2​+A=U1​⊔U2​∑​FU1​×G(U2​⊔{∗})A=U1​⊔U2​∑​F′U1​×GU2​+A=U1​⊔U2​∑​FU1​×G′U2​(F′∙G)A+(F∙G′)A​となりライプニッツ則が成り立つことが分かります。2行目から3行目へは A⊔{∗}A\sqcup\{*\}A⊔{∗} の非交和な2分割が AAA の非交和な2分割 A=U1⊔U2A=U_1\sqcup U_2A=U1​⊔U2​ に対して U1U_1U1​ に ∗*∗ を追加する場合と U2U_2U2​ に ∗*∗ を追加する場合に分けて考えられることを利用しています。
更に合成の微分は
(F∘G)′A=(F∘G)(A⊔{∗})=∑π∈P(A⊔{∗})(Fπ×∏B∈πGB)=∑A=U1⊔U2(∑π∈P(U1)(F(π⊔{∗})×∏B∈πGB×G(U2⊔{∗})))=∑A=U1⊔U2(∑π∈P(U1)(F′π×∏B∈πGB×G′U2))=∑A=U1⊔U2(∑π∈P(U1)(F′π×∏B∈πGB))×G′U2=∑A=U1⊔U2(F′∘G)U1×G′U2=((F′∘G)∙G′)A
\begin{matrix}
(F\circ G)'A
&=& (F\circ G)(A\sqcup\{*\}) \\
&=& \displaystyle\sum_{\pi\in P(A\sqcup\{*\})}\left(F\pi\times\prod_{B\in\pi}GB\right) \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2}\left(\sum_{\pi\in P(U_1)}\left(F(\pi\sqcup\{*\})\times\prod_{B\in\pi}GB\times G(U_2\sqcup\{*\})\right)\right) \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2}\left(\sum_{\pi\in P(U_1)}\left(F'\pi\times\prod_{B\in\pi}GB\times G'U_2\right)\right) \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2}\left(\sum_{\pi\in P(U_1)}\left(F'\pi\times\prod_{B\in\pi}GB\right)\right)\times G'U_2 \\
&=& \displaystyle\sum_{A=U_1\sqcup U_2}(F'\circ G)U_1\times G'U_2 \\
&=& ((F'\circ G)\bullet G')A \\
\end{matrix}
(F∘G)′A​=======​(F∘G)(A⊔{∗})π∈P(A⊔{∗})∑​(Fπ×B∈π∏​GB)A=U1​⊔U2​∑​​π∈P(U1​)∑​(F(π⊔{∗})×B∈π∏​GB×G(U2​⊔{∗}))​A=U1​⊔U2​∑​​π∈P(U1​)∑​(F′π×B∈π∏​GB×G′U2​)​A=U1​⊔U2​∑​​π∈P(U1​)∑​(F′π×B∈π∏​GB)​×G′U2​A=U1​⊔U2​∑​(F′∘G)U1​×G′U2​((F′∘G)∙G′)A​となり合成関数の微分法が成り立つことが分かります。2行目から3行目はA⊔{∗}A\sqcup\{*\}A⊔{∗}の非交和な分割を考えた時に ∗*∗ を含んでいる集合を U2⊔{∗}U_2\sqcup\{*\}U2​⊔{∗} と置くと A=U1⊔U2A=U_1\sqcup U_2A=U1​⊔U2​ という AAA の非交和な分割に対して元の非交和な分割が、ある π∈P(U1)\pi\in P(U_1)π∈P(U1​) を使って π⊔{U2⊔{∗}}\pi\sqcup\{U_2\sqcup\{*\}\}π⊔{U2​⊔{∗}} と表せることを利用しています。3行目の式における F(π⊔{∗})F(\pi\sqcup\{*\})F(π⊔{∗}) の ∗*∗ は集合を要素とする1点集合{U2⊔{∗}}\{U_2\sqcup\{*\}\}{U2​⊔{∗}} に対応しています（ FFF の引き数に現れる ∗*∗ と GGG の引き数に現れる ∗*∗ の意味が異なるのでややこしい…）。
これらの例と母関数の対応を考えることにより Combinatorial Species の微分の母関数は元の母関数の微分に対応する ことも分かるでしょう。
さてこの Combinatorial Species の微分を用いて 代数的データ型の微分 を考えましょう。すなわち代数的データ型の微分を元の代数的データ型に対応する Combinatorial Species を微分した Combinatorial Species に対応する代数的データ型とするのです。
例えば List a に対応する Combinatorial Species LLL の母関数の微分を考えると
L′(x)=(11−x)′=(11−x)2=L(x)2
\begin{matrix}
L'(x)
&=& \left(\frac{1}{1-x}\right)' \\
&=& \left(\frac{1}{1-x}\right)^2 \\
&=& L(x)^2 \\
\end{matrix}
L′(x)​===​(1−x1​)′(1−x1​)2L(x)2​となり List a の微分は (List a, List a) に同型な型であることが分かります。実はこれは List a の Zipper と同じ型になっており、一般にデータ型の Zipper を得る操作はデータ型を微分していると解釈することができます[5]。

 まとめ以上の話より以下のような対応表が書けることが分かりました。


型
Combinatorial Species
母関数


data Void
000
000

data One = One
111
111

type Two = Sum One One
1+11+11+1
1+1=21+1=21+1=2

data Maybe a = Nothing | Just a
1+X1 + X1+X
1+x1+x1+x

data Sum a b = A a | B b
A+BA + BA+B
A(x)+B(x)A(x)+B(x)A(x)+B(x)

data Product a b = Product a b
A∙BA \bullet BA∙B
A(x)×B(x)A(x)\times B(x)A(x)×B(x)

data Compose f g a = Compose (f (g a))
F∘GF \circ GF∘G
F(G(x))F(G(x))F(G(x))

データ型Fの微分
F′F'F′
F(x)′F(x)'F(x)′

代数的データ型に対応する多項式を Combinatorial Species を経由してから母関数として得ることで ラベル付けられた構造の集合という直感的なイメージを持ちながら微分といった深い構造にも言及できるようになる のが、Combinatorial Species として考えることの面白さの一つかと思います。
この解釈の欠点を挙げるとすれば関数の型 a -> b に言及できていないことがあるかもしれません。定数から定数への対応なら同型対応を使ってなんとか考えられるかもしれませんが、一般には対応する母関数の演算が g(x)f(x)g(x)^{f(x)}g(x)f(x) や項ごとの冪となることが期待されるため多項式に閉じなくなり難しいかもしれません。
他にも Combinatorial Species には色々な拡張が考えられており、複数の引き数を取れるにように拡張した Multisort Species（Implicit Species Theorem を厳密に述べるためにも必要。偏微分も定義できる）や、足し算だけでなく引き算も考えられるように拡張した Virtual Species や[6]、Combinatorial Species の左Kan拡張として Analytic Functor （ドメインが有限集合の圏 B{\mathcal B}B から集合の圏 SetSetSet に拡張される。"テイラー展開"を持つような関手）といったものが挙げられます。
最後に、もし今回の話に興味があれば以下の文献を読むのがおすすめです。
Species and Functors and Types, Oh My!
Combinatorial Species and Labelled Structures
挿絵イラスト: Loose Drawing
＼読んでいただきありがとうございました！／

この記事が面白かったら いいね♡ をいただけると嬉しいです☺️

バッジを贈っていただければ次の記事を書くため励みになります🙌

脚注
A History of Haskell: being lazy with class ↩︎
基本的な型を考えている限り型を集合と捉えることはうまくいきますが、例えば T a = (a -> Bool) -> Bool という関手の不動点を考えると濃度に関する議論がうまくいかなくなるといった例外があり（Polymorphism is not set theoretic）一般的には型と集合は異なるものです ↩︎
A quick introduction to species, operads, and closed multicategories ↩︎
Species and Functors and Types, Oh My! ↩︎
Haskell/Zippers - Wikibooks ↩︎
Species subtraction made simple ↩︎
型	集合	要素の数
`data Void`	$\emptyset$	$0$
`data One = One`	$\{*\}$	$1$
`type Two = Sum One One`	$\{\}+\{\}$	$1+1=2$
`data Maybe a = Nothing \| Just a`	$\{*\} + A$	$1+\|A\|$
`data Sum a b = A a \| B b`	$A \sqcup B$	$\|A\|+\|B\|$
`data Product a b = Product a b`	$A \times B$	$\|A\|\times\|B\|$
`a -> b`	$B^A$	$\|B\|^{\|A\|}$
型	Combinatorial Species	母関数
`data Void`	$0$	$0$
`data One = One`	$1$	$1$
`type Two = Sum One One`	$1+1$	$1+1=2$
`data Maybe a = Nothing \| Just a`	$1 + X$	$1+x$
`data Sum a b = A a \| B b`	$A + B$	$A(x)+B(x)$
`data Product a b = Product a b`	$A \bullet B$	$A(x)\times B(x)$
`data Compose f g a = Compose (f (g a))`	$F \circ G$	$F(G(x))$
データ型Fの微分	$F'$	$F(x)'$
Discussion

ログインするとコメントできます