Open7

データ操作いろいろ　後でまとめる

piyokopiyoko

データ操作

読み込み

import pandas as pd
df = df.read_csv('パス')

1列分のデータを抽出

df_gender = df['性別']

グループ化

group_gender = df.groupby['性別']
# group_gender の型は pandas.core.groupby.generic.DataFrameGroupBy

年齢でグループ化したデータから、男性データを取り出す

male_data = group_gender.get_group('男性')
#male_data の型は pandas.core.frame.DataFrame

年齢でグループ化したデータから、男性データを取り出し、年齢列のデータのみ取り出す

male_data = group_gender.get_group('男性')['年齢']
#male_data の型は pandas.core.frame.DataFrame
piyokopiyoko

集計操作

読み込み

import pandas as pd
df = df.read_csv('パス')

クロス集計

# 行が性別、列が評価
pd.crosstab(df['性別'], df['評価'])
# 行が評価、列が性別
pd.crosstab(df['評価'], df['性別'])
piyokopiyoko

用語集

統計的仮説検定

統計的仮説検定は、データを基にある仮説が正しいかどうかを判断するための方法です。具体的には、以下のステップを含みます：

**帰無仮説（H0）と対立仮説（H1またはHa）**の設定：帰無仮説は「効果がない」や「違いがない」といった仮説で、対立仮説は「効果がある」や「違いがある」といった仮説です。
検定統計量の計算：データから計算した数値をもとに検定統計量を求めます。
p値の算出：検定統計量を使って、帰無仮説が正しいとした場合に得られるデータの確率（p値）を計算します。
帰無仮説の棄却または採択：p値が事前に設定した有意水準（通常は0.05）より小さい場合、帰無仮説を棄却し、対立仮説を支持します。

探索的データ分析（EDA: Exploratory Data Analysis）

探索的データ分析は、データセットを視覚的に調査して、データの構造、パターン、異常値、関係性などを見つけ出すプロセスです。EDAの主な目的は、データの概要を把握し、後の分析に向けた仮説を立てるための知見を得ることです。主な手法には、以下が含まれます：

記述統計量の計算（平均、中央値、標準偏差など）
グラフ（ヒストグラム、散布図、箱ひげ図など）による視覚化
相関分析や回帰分析による関係性の調査

確証的データ分析（CDA: Confirmatory Data Analysis）

確証的データ分析は、事前に立てた仮説や理論に基づいてデータを分析し、その仮説の正しさを検証する手法です。確証的データ分析は、データの特定の側面や理論的な仮説を検証するために使用されます。主な手法には、以下が含まれます：

仮説検定：特定の仮説がデータに合致しているかどうかを判断します。
モデルの適合度検査：データに対してモデルがどれだけ適合しているかを検討します。
因子分析や構造方程式モデリング（SEM）：複数の変数間の関係を検証します。
EDAがデータの理解を深めるための「探索」のプロセスであるのに対し、CDAは事前の仮説を検証するための「確認」のプロセスです。

piyokopiyoko

データをカテゴライズする

# 1週間当たりの勉強に費やす時間の値が細かすぎて、解析しにくいので、1週間の平均でカテゴライズしてみる
# cut:カテゴライズする
# range（start, stop, step）※stopの値は含まれないので注意
# right=Trueで右側の境界値を入れる

df['Study Hours LANK'] = pd.cut(df['Study Hours'], bins=range(0, 70, 7), right=True)
df['Study Hours LANK'] .unique()

# 'Study Hours LANK' を数値に変換
df['Study Hours LANK'] = df['Study Hours LANK'].cat.codes
piyokopiyoko

データをQueryで操作する

列名にスペースが入っていると正常に動かないのでバッククォートで囲む

query1 = df.query('`Study Hours LANK` <= 42')
query2 = df.query('`Study Hours LANK` > 42')
piyokopiyoko

スケーリングの最も一般的な方法は次の2つになります

  • 標準化（Standardization）: 平均を0、標準偏差を1にする方法
  • 正規化（Normalization）: 値を0から1の範囲にスケーリングする方法

今回は 標準化 でスケーリングしてみます。

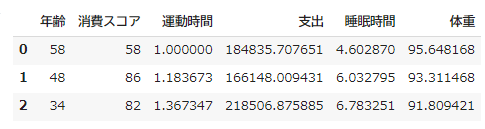
まずはデータを確認してみます

df.head(3)

説明変数を作成します。
データフレームから文字列項目の「名前」と目的変数「収入」を取り除いたものが、今回の説明変数になります。
元のデータフレームから dropメソッドで名前と収入を削除しています。
axis=1は列方向の削除です。

x = df.drop(['名前', '収入'], axis=1)

# 必要な項目だけを取り出してもOKです
# x = df[['年齢','収入','消費スコア','運動時間','支出','睡眠時間','体重']]

x.head(3)


説明変数の標準化を行います。
標準化は sklearn（サーキットラーン）ライブラリのStandardScalerクラスのfit_transformメソッドを使用します。

# sklearnライブラリをインポート
from sklearn.preprocessing import StandardScaler
# StandardScalerクラスをインスタンス化
scaler = StandardScaler()
# 標準化
x_std = scaler.fit_transform(x)
x_std

標準化後はpandasのDataFrame型からnumpyのndarray型になります

type(x_std)

ndarray型 だと見づらいのでpandasのDataFrame型に変換して値を確認してみます

colnms =x.columns
df_x_std = pd.DataFrame(x_std, columns=colnms)
df_x_std.head()
piyokopiyoko

外れ値の削除

とりあえず

df_filtered = df[df[target] <= 120]

箱ひげ図を書いて確認

箱ひげ図

sns.boxplot(y=target, data=df)
plt.title(f'{target} Boxplot')
plt.show()

箱ひげ図の上限（または下限）を超えている点は、データの分布の大部分から離れた値であり、外れ値とみなされます。
**四分位範囲（IQR）**を基に、1.5倍の範囲を超えた値が外れ値として表示されます。

# 四分位範囲（IQR）を計算
Q1 = df['filedname'].quantile(0.25)
Q3 = df['filedname'].quantile(0.75)
IQR = Q3 - Q1

# 外れ値の範囲を計算
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 外れ値を除去
df_no_outliers = df[(df['filedname'] >= lower_bound) & (df['filedname'] <= upper_bound)]

# 外れ値を取り除いたデータで再度箱ひげ図を描画
sns.boxplot(y='filedname', data=df_no_outliers)
plt.title('filedname Boxplot (Without Outliers)')
plt.show()

四分位範囲（IQR）とは：
**IQR（Interquartile Range）**は、データの第1四分位点（Q1: データの下位25%点）と第3四分位点（Q3: データの上位25%点）の差です。データの中央50%がこの範囲に収まることを意味します。
外れ値の定義（IQRを使用）：
外れ値を判定する際に、Q1 - 1.5 * IQRより小さい値、またはQ3 + 1.5 * IQRより大きい値が外れ値とみなされます。

下限値: Q1 - 1.5 * IQR
上限値: Q3 + 1.5 * IQR
1.5倍の基準について：
1.5倍は、一般的に使われる外れ値の基準で、データの範囲外に大きく外れた値を見つけるのに有効です。この基準は、特定の目的に応じて適度なバランスを持っており、ほとんどのケースで使われます。

ただし、場合によっては、データの特性や外れ値の影響を考慮して、**3倍（厳しい基準）や、逆に1.0倍（緩い基準）**など、基準を変更することもあります。

まとめ：
1.5倍のIQRは、外れ値を検出するための一般的で標準的な基準です。
データの特性や目的に応じて、基準を調整することも可能です。

メソッド化しておく

def remove_outliers(df, column):
    # 四分位範囲（IQR）を計算
    Q1 = df[column].quantile(0.25)
    Q3 = df[column].quantile(0.75)
    IQR = Q3 - Q1
    # 外れ値の範囲を計算
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    # 外れ値を除去
    return df[(df[column] >= lower_bound) & (df[column] <= upper_bound)]


df = remove_outliers(df, 'Age')