データ分析 2群間の代表値の検定:実践例2
前回までの記事です
前回に続き、より実践ベースでの検定を行ってみたいと思います
使用したデータ
あるジュエリーショップのアンケート結果を集めたデータです。
使用したデータ
データは適当に作ったものです
| 性別 | 年齢 | 購入形態 | 購入の目的 | 商品のデザイン | 納品の迅速さ | サイトの使いやすさ | 価格の妥当性 | 商品への満足度 | ショップの雰囲気 | スタッフの対応 | アフターサービス | 包装の状態 | 満足度 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 女性 | 50 | プレゼント用 | 記念日 | 4 | 4 | 4 | 4 | 3 | 4 | 4 | 4 | 4 | 4 |
| 女性 | 35 | 自分用 | 婚約 | 4 | 5 | 4 | 4 | 1 | 1 | 5 | 4 | 1 | 2 |
| 女性 | 22 | プレゼント用 | 日常使い | 1 | 1 | 1 | 4 | 1 | 5 | 1 | 3 | 1 | 3 |
| 男性 | 30 | 自分用 | 記念日 | 3 | 4 | 3 | 4 | 5 | 1 | 4 | 4 | 5 | 3 |
| 男性 | 59 | プレゼント用 | 婚約 | 4 | 3 | 3 | 3 | 4 | 4 | 3 | 5 | 4 | 4 |
| 男性 | 52 | プレゼント用 | 日常使い | 2 | 3 | 3 | 3 | 2 | 2 | 1 | 3 | 2 | 2 |
| 男性 | 10 | 自分用 | 記念日 | 2 | 5 | 1 | 3 | 3 | 3 | 5 | 5 | 3 | 3 |
| 女性 | 19 | 自分用 | 婚約 | 3 | 5 | 2 | 4 | 2 | 5 | 5 | 5 | 5 | 4 |
| 女性 | 24 | プレゼント用 | 日常使い | 4 | 2 | 3 | 4 | 1 | 1 | 4 | 4 | 1 | 2 |
| 女性 | 39 | プレゼント用 | 記念日 | 5 | 5 | 5 | 5 | 3 | 5 | 5 | 4 | 5 | 5 |
| 女性 | 55 | プレゼント用 | 婚約 | 3 | 5 | 5 | 5 | 1 | 3 | 2 | 3 | 4 | 3 |
| 女性 | 59 | 自分用 | 日常使い | 1 | 3 | 1 | 3 | 3 | 3 | 4 | 4 | 2 | 2 |
| 男性 | 30 | プレゼント用 | 記念日 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 3 |
| 男性 | 58 | プレゼント用 | 婚約 | 2 | 2 | 2 | 2 | 2 | 4 | 3 | 4 | 4 | 3 |
以下略
テーマ
満足度に対して商品のデザインは何らかの影響があるかを分析してみます。
分析
必要なライブラリをインストールし、データを読み込んでおきます
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
plt.style.use("seaborn")
plt.rcParams['font.family'] = 'IPAexGothic'
plt.figure(figsize=(10, 5))
# データ読込
df = pd.read_csv('/content/drive/MyDrive/jewelry_shop_reviews.csv')
df.head(3)
まずはデータを確認して欠損値の有無などを確認しておきます
df.info()
データ数は1000件で欠損値はありません。

商品のデザインの評価ごとに満足度の、それぞれの平均値と中央値を確認してみます
# 商品のデザインをグループ化し満足度を抽出する
group1 = df.groupby('商品のデザイン')['満足度']
# 平均値と中央値を確認する
group1 .agg(['mean', 'median'])
商品のデザインに 4, 5 を付けた人は、満足度も 4 と高い傾向にあるようです
| 商品のデザイン | mean | median |
|---|---|---|
| 1 | 2.476460578559274 | 3.0 |
| 2 | 2.807233704292528 | 3.0 |
| 3 | 3.2211684370257965 | 3.0 |
| 4 | 3.727364185110664 | 4.0 |
| 5 | 4.274384685505925 | 4.0 |
商品デザインの評価を1,2,3としたグループと 商品のデザインの評価を4.5としたグループに分けて、検定してみたいと思います。
# 商品デザインの評価を1,2,3としたグループと 商品のデザインの評価を4.5としたグループに分けて満足度を抽出します。
query1 = df.query('商品のデザイン <= 3')['満足度']
# group1 = df[df['商品のデザイン'] <= 3]['満足度']でもOK
query2 = df.query('商品のデザイン > 3')['満足度']
# group2 = df[df['商品のデザイン'] > 3]['満足度'] でもOK
商品デザインの評価を1,2,3としたグループの平均値と中央値を確認します
query1.agg(['mean', 'median'])

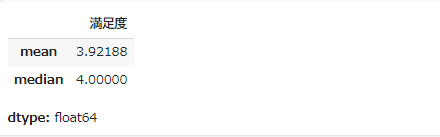
商品デザインの評価を4,5 としたグループの平均値と中央値を確認します
query2.agg(['mean', 'median'])
検定の目的
商品デザインの評価を1,2,3としたグループ と 商品のデザインの評価を4.5としたグループ で満足度の平均値の違いが母集団でも有意な差かどうかを検定してみます。
商品デザインの評価を1,2,3の満足度の平均と、商品のデザインの評価を4.5の満足度の平均の差が、標本集団だけでなく母集団でも有意な差であるとすれば、商品デザインの評価の違いは満足度に影響を及ぼしていると判断できます。
それでは商品デザインの評価を1,2,3としたグループ と 商品のデザインの評価を4.5としたグループ での平均値の差が母集団でも有意な差であるかを検定してみます。
仮説:商品デザインの評価によって、満足度に差がある
正規性を確認
まずは使用する検定を判断するために、商品デザインの評価を1,2,3グループと商品のデザインの評価を4.5グループの正規性の確認を行います。
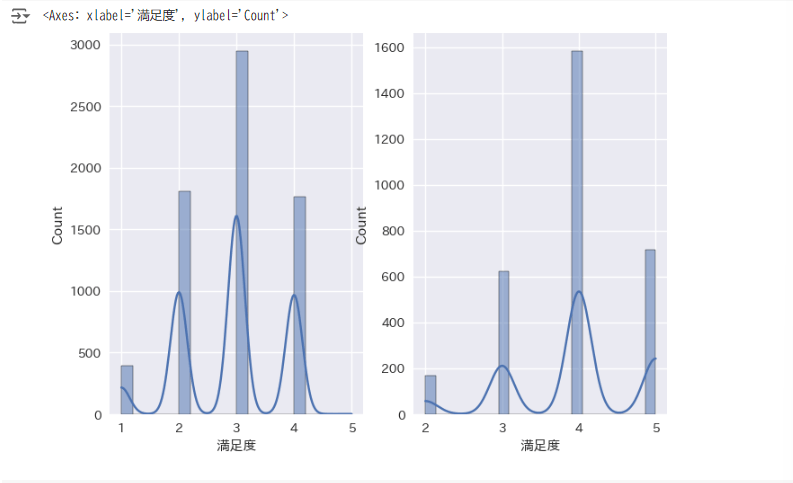
まずは正規性を可視化で確認してみます。
plt.subplot(1, 2, 1)
sns.histplot(query1, kde=True)
plt.subplot(1, 2, 2)
sns.histplot(query2, kde=True)
グラフからは正規性があるのではないかと思われます
検定
正規性の検定を行って検証してみます。
データ数が多いのでコルモゴロフ・スミルノフ検定を使用します。
- 帰無仮説:正規分布である
- 対立仮説:正規分布でない
商品デザインの評価を1,2,3グループの正規性を確認してみます
stats.kstest(query1, "norm")
KstestResult(statistic=0.920416896251387, pvalue=0.0, statistic_location=2, statistic_sign=-1)
有意水準 0.05 > P値 0 なので 帰無仮説を棄却し、正規分布でないとなります
商品のデザインの評価を4.5グループの正規性を確認してみます
stats.kstest(query2, "norm")
KstestResult(statistic=0.9772498680518208, pvalue=0.0, statistic_location=2, statistic_sign=-1)
有意水準 0.05 > P値 0 なので 帰無仮説を棄却し、正規分布でないとなります
男性データも女性データも正規分布ではないので
「ノンパラメトリック」で「データに対応がない」場合になり、「マンホイットニーのU検定」を使用します。
帰無仮説:平均値に有意な差はない
対立仮説:平均値に有意な差がある
stats.mannwhitneyu(query1, query2, alternative='two-sided')
有意水準 0.05 > P値 0. → 帰無仮説を棄却し、平均値に有意な差がある となりました。
検定の結果:
商品のデザインは満足度に影響を及ぼしている
Discussion