データ分析 2群間の代表値の検定:マンホイットニーのU検定/ウィルコクソン順位和検定
以前まとめた2群間の代表値の検定について、具体的な手法を簡単にまとめてみます。
python + google colaboratory で 実行しています。
テーマ
あるカフェチェーンが新しいマーケティングキャンペーンの効果を評価するために、
2つの異なるキャンペーンを実施しました。
1つのキャンペーンは「キャンペーンA」、もう1つは「キャンペーンB」と名付けられ、
それぞれ異なる10店舗で行われました。
1ヶ月間の売上データを集計した結果、
キャンペーンAの平均売上は750,000円、
キャンペーンBの平均売上は680,500円でした。
この売上の差は統計的に有意と言えるでしょうか?
使用したデータ
カフェチェーンの売上データを想定しています。
| No | キャンペーンA売上 | キャンペーンB売上 |
|---|---|---|
| 1 | 450 | 325 |
| 2 | 480 | 930 |
| 3 | 525 | 458 |
| 4 | 691 | 982 |
| 5 | 738 | 341 |
| 6 | 715 | 340 |
| 7 | 732 | 380 |
| 8 | 503 | 820 |
| 9 | 763 | 964 |
| 10 | 974 | 673 |
前準備
グラフに日本語ラベルを表示できるように japanize-matplotlib をインストールします。
!pip install -q japanize-matplotlib
必要のライブラリをインポートして、使用するデータを読み込んでおきます。
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
# データ読込
df = pd.read_csv('/content/drive/MyDrive/cofee_sales.csv')
df
キャンペーンA売上 と キャンペーンB売上 のデータの代表値を確認
キャンペーンA売上 と キャンペーンB売上 の平均値を確認する
df.mean()

キャンペーンA売上 と キャンペーンB売上 の中央値を確認する
df.median()
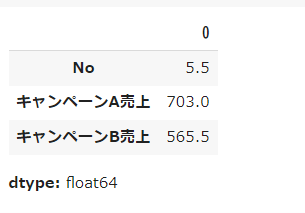
平均値にも中央値にも、キャンペーンAとキャンペーンBに差があります。
この差は標本集団だけの差なのか、母集団でも意味ある差なのかを検定していきます。
使用する検定を決定する
1.正規性を視覚的に確認する
まずは使用する検定を特定するために、データが正規性に従っているかを確認します。
キャンペーンA売上データとキャンペーンB売上データの値をヒストグラムで可視化して正規性を確認してみます。
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
sns.histplot(df['キャンペーンA売上'], kde=True)
plt.subplot(1,2,2)
sns.histplot(df['キャンペーンB売上'], kde=True)
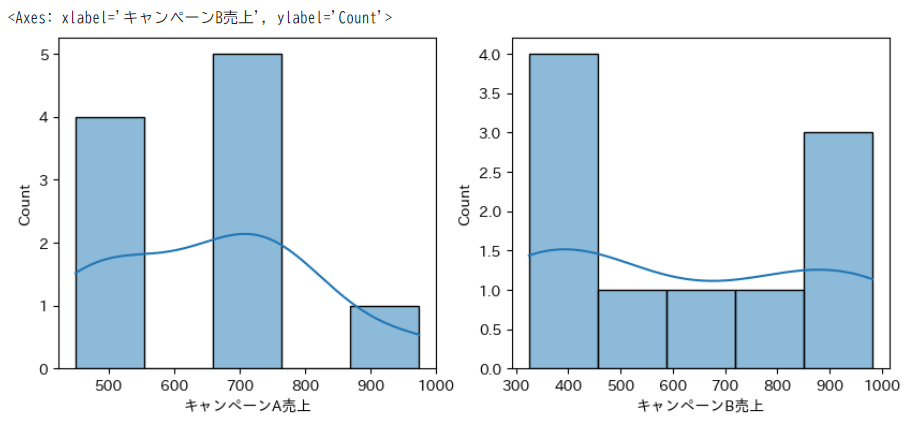
2.正規性を統計的に確認
視覚だけでなく統計的にも正規分布に従っているかを確認します。
正規性を確認する代表的な検定方法には下記のような検定があります。
- シャピロ・ウィルク検定(S-W検定)
- 小さいデータセットに適しています
- scipy の shapiroメソッドを使用
- コルモゴロフ・スミルノフ検定(K-S検定)
- 広く使われています
- scipy の kstestメソッドを使用
- Anderson-Darling検定
- シャピロ・ウィルク検定よりも詳細な正規性の確認ができます。
- Q-Qプロット
- 視覚的にデータの正規性を確認するのに便利です。
今回はデータセットが小さいので シャピロ・ウィルク検定 を使用して正規性を検定します。
シャピロ・ウィルク検定 は scipy の shapiroメソッドを使用します。
帰無仮説:正規分布である
対立仮説:正規分布でない
P値が0.05より小さい場合、帰無仮説を棄却し、データは正規分布に従っていないと判断します。
from scipy import stats
stats.shapiro(データ)
ちなみに、データセットが多い場合は コルモゴロフ・スミルノフ検定 を使用します
コルモゴロフ・スミルノフ検定 は scipy の kstestメソッドを使用します。
正規性を検定する際は kstest メソッドの第二引数に'"norm"'を指定します。
from scipy import stats
stats.kstest(データ, "norm")
正規性を検定する
それでは、実際にキャンペーンA売上 と キャンペーンB売上 の それぞれのデータを検定してみます。
キャンペーンA売上データの正規性を検定する
stats.shapiro(df['キャンペーンA売上'])
ShapiroResult(statistic=0.9081003208727657, pvalue=0.26819550619717003)
P値(pvalue)=0.265 と 優位水準を0.05を上回っていますので、帰無仮説を棄却できず
キャンペーンA売上データは正規分布に従っていると判断します。
キャンペーンB売上データの正規性を検定する
stats.shapiro(df['キャンペーンB売上'])
ShapiroResult(statistic=0.8311712939353156, pvalue=0.034565274492012826)
P値(pvalue)=0.03 と 優位水準を0.05を下回っていますので、帰無仮説を棄却し
キャンペーンB売上データは正規分布に従っていないと判断します。
3.使用する検定を決める
キャンペーンA売上データ は正規分に従いますが、キャンペーンB売上データは正規分布に従わないので「ノンパラメトリック検定」で、かつ 比較の対処が異なるので「対応なし」データになります。
よって、今回使う検定は「マンホイットニーのU検定」または「ウィルコクソン順位和検定」となります。

マンホイットニーのU検定、ウィルコクソン順位和検定のどちらを使用しても問題ありません。
マンホイットニーのU検定は scipy の mannwhitneyu メソッドを使用します。
from scipy import stats
stats.mannwhitneyu(df['キャンペーンA売上'], df['キャンペーンB売上'])
ウィルコクソン順位和検定は scipy の wilcoxon メソッドを使用します。
from scipy import stats
stats.wilcoxon(df['キャンペーンA売上'], df['キャンペーンB売上'])
検定を行う
それでは実際に検定を行います。
1.仮説立て
- 帰無仮説:2群間の平均値に有意な差はない
- 対立仮説:2群間の平均値に有意な差はある
2.優位水準
- 5%
3.判定(マンホイットニーのU検定)
stats.mannwhitneyu(df['キャンペーンA売上'], df['キャンペーンB売上'])
出力結果
MannwhitneyuResult(statistic=58.0, pvalue=0.5707503880581739)
P値(pvalue)は「0.570」と有意水準より大きいので
有意水準 < P値 となり 帰無仮説は棄却できず、キャンペーンAとキャンペーンBに有意な差はないとなります。
3.判定(ウィルコクソン順位和検定)
ウィルコクソン順位和検定でも確かめてみます
stats.wilcoxon(df['キャンペーンA売上'], df['キャンペーンB売上'])
出力結果
WilcoxonResult(statistic=23.0, pvalue=0.6953125)
こちらもP値(pvalue)は「0.695」と有意水準より大きいので
有意水準 < P値 となり 帰無仮説は棄却できず、キャンペーンAとキャンペーンBに有意な差はないとなります。
4.結論
キャンペーンAとキャンペーンBは売上に有意な影響を与えていないと判断できる。
以上で、今回の検定は終了です。
Discussion