社会人大学生による、エンジニアが数学をちょっとだけ好きになる話
はじめに
エンジニアとして働き始めてから3年が経ち、ソフトウェア開発について多くのことを学んできました。最近の技術の進化により、ほとんどのツールは誰でも簡単に理解し、使えるようになったと感じています。しかし、技術の本質的な部分に踏み込むと、途端に理解に苦労するといった経験をしてきました。
表面的な技術だけでなく、今日の技術の基礎となる教養を身につけたいと考え、現在はログラスで働きながら、通信制大学で情報工学を勉強しています。
大学で勉強した数学のおかげで、ソフトウェアの開発手法や言語仕様の根底となる原則や考え方が以前よりも理解しやすくなったと感じます。この記事では、ソフトウェア技術と数学の紐付きを紹介し、ソフトウェア技術を数学的視点で考察しようと思います。
*この記事で紹介する数学の知識は、高校もしくは大学初期に学ぶ基本的な 集合論、特に写像が中心です。
プログラミングの関数を数学的に考える
プログラミングにおける関数とは、一般的に特定のタスクを実行するために定義されたコードブロックです。関数は、入力(引数)を受け取り、処理を行った結果を出力(戻り値)として返します。
// 引数を二乗する
def square(a):
return a * a
上記の関数を数学的に表すと、以下の二次関数になります。
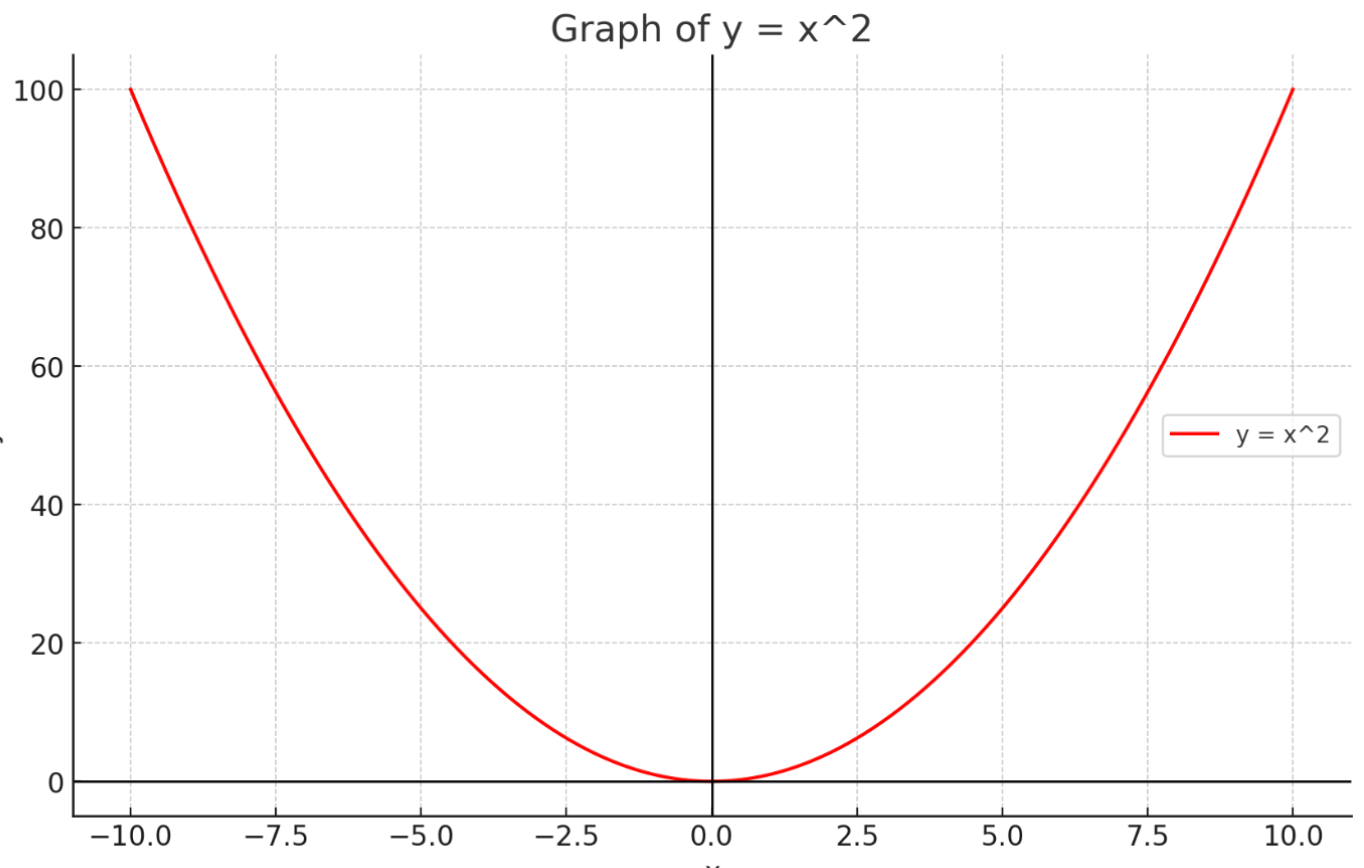
この二次関数も、プログラミングの関数と同様に入力(x)を受け取り、処理を行って 出力(y)を返しています。
一方で、実用的なプログラミングでは、数値だけでなく文字列やデータ構造など、さまざまな種類の入出力を行います。次のセクションでは、それらの対応関係を数学的に捉えるための概念である 写像(mapping) という概念を紹介します。
写像の基本
国コードのから国名を割り出す処理をプログラムで書いてみます。
// 国コードから国名を取得する処理で、便宜的に4カ国のみ
def get_country_name(country_code):
country_dict = {
"US": "United States",
"JP": "Japan",
"IN": "India",
"IT": "Italy",
}
この処理を数学的に表現しようとするとどうなるでしょうか?
前述した二次関数(y=x^2)のように数値のグラフで表すことはできません。ここで 写像(mapping) という概念を紹介します。
写像(mapping) とは、ある集合の要素を別の集合の要素に 「対応」 させるルールのことです。
f : A → B : 集合Aと集合Bを対応する写像f
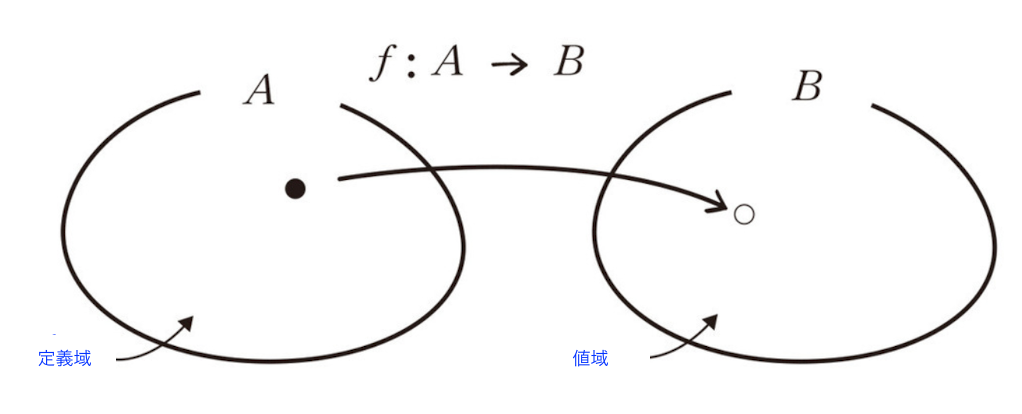
入力側の集合を 定義域(domain) 、出力側の集合 値域(codomain) と呼びます。
写像の条件として、始集合の任意の要素に対して、終集合の中から一つだけの要素が対応付けられる必要があります。つまり、ある入力に対して出力が一つに決まります。以下のように入力に対して得られる出力が複数存在する場合、それは写像ではありません。
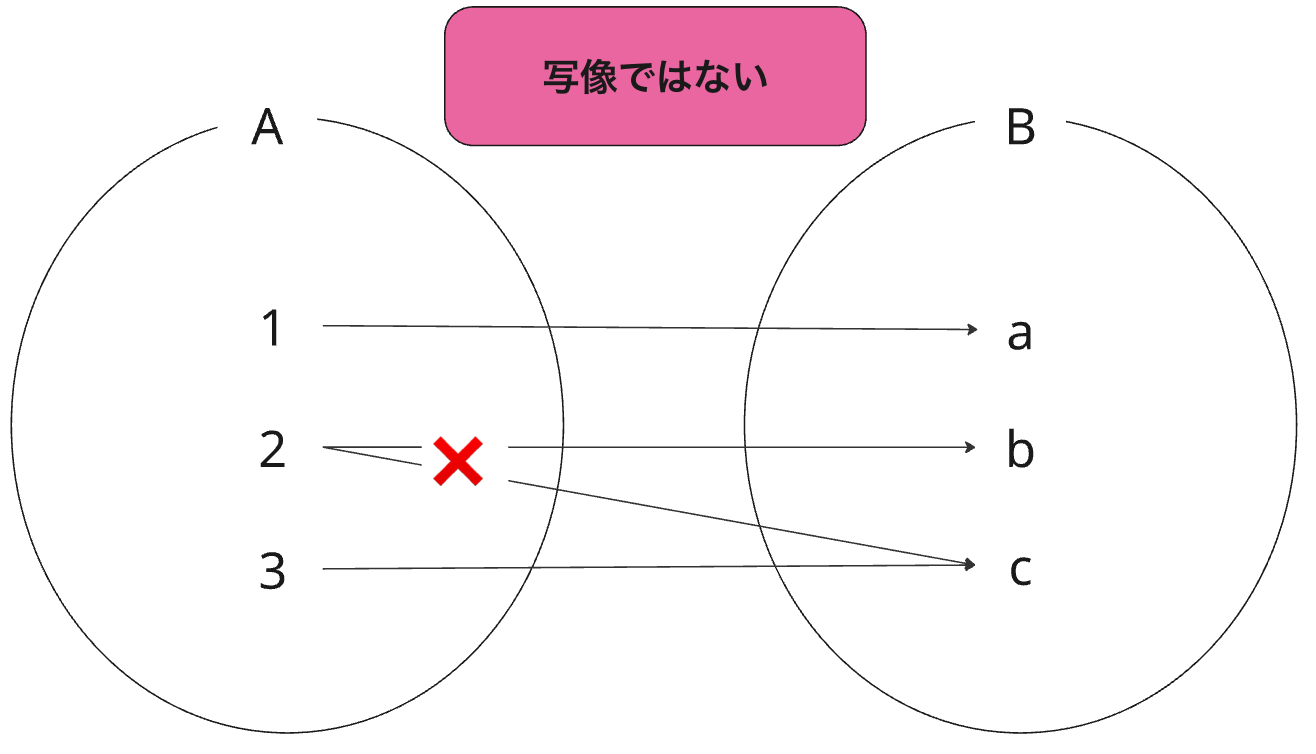
例えば、国コードと国名の対応を写像で表すと以下のようになります。
f : 国コードの集合 → 国名の集合 : 国コードの集合と国名の集合を対応する写像f
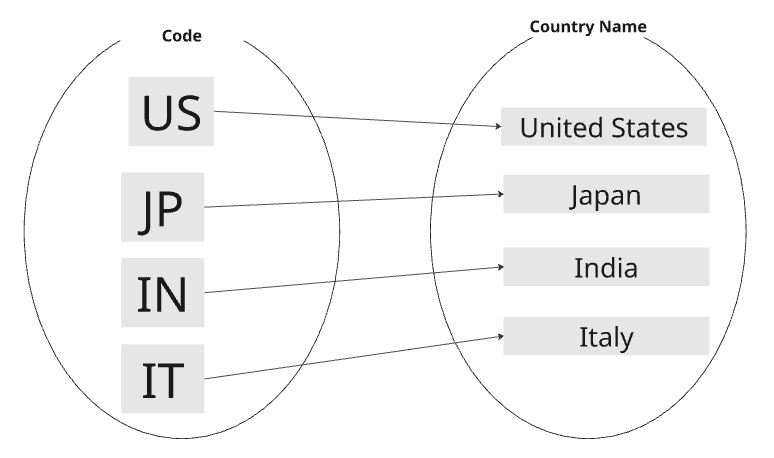
「出入力を扱うシステムは写像で表現できそうだ」と感じていただけことを祈って、次のセクションで写像について詳しく紹介します。
写像の種類と応用
身近な例を用いて、写像の種類を紹介します。
-
全射(surjection)
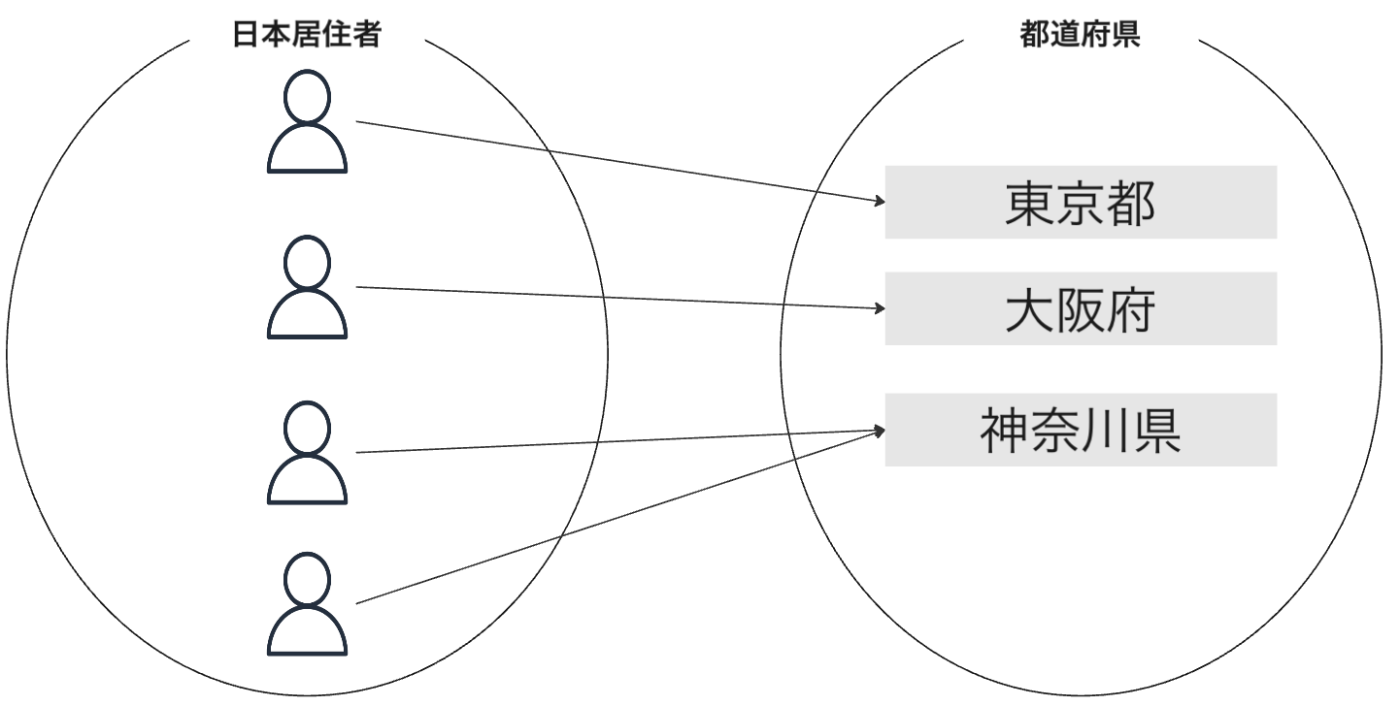
日本居住者の集合と、居住地の都道府県の集合を考えます。
すべての都道府県に住民がいるため、都道府県の各要素に必ず対応する居住者が存在します。このように、終集合のすべての要素 が、少なくとも一つの始集合の要素と対応する写像を全射 と呼びます。
-
単射(injective)
予約番号と空席のある飛行機の座席の対応を考えてみます。空席の座席は対応する予約番号が存在しません。一方、予約された座席は、必ず一つの予約番号と対応し、複数の予約番号と対応することはありません。このように 始集合の要素が、終集合の要素へ一意に対応する写像 を 単射 と呼びます。

-
全単射(bijection)
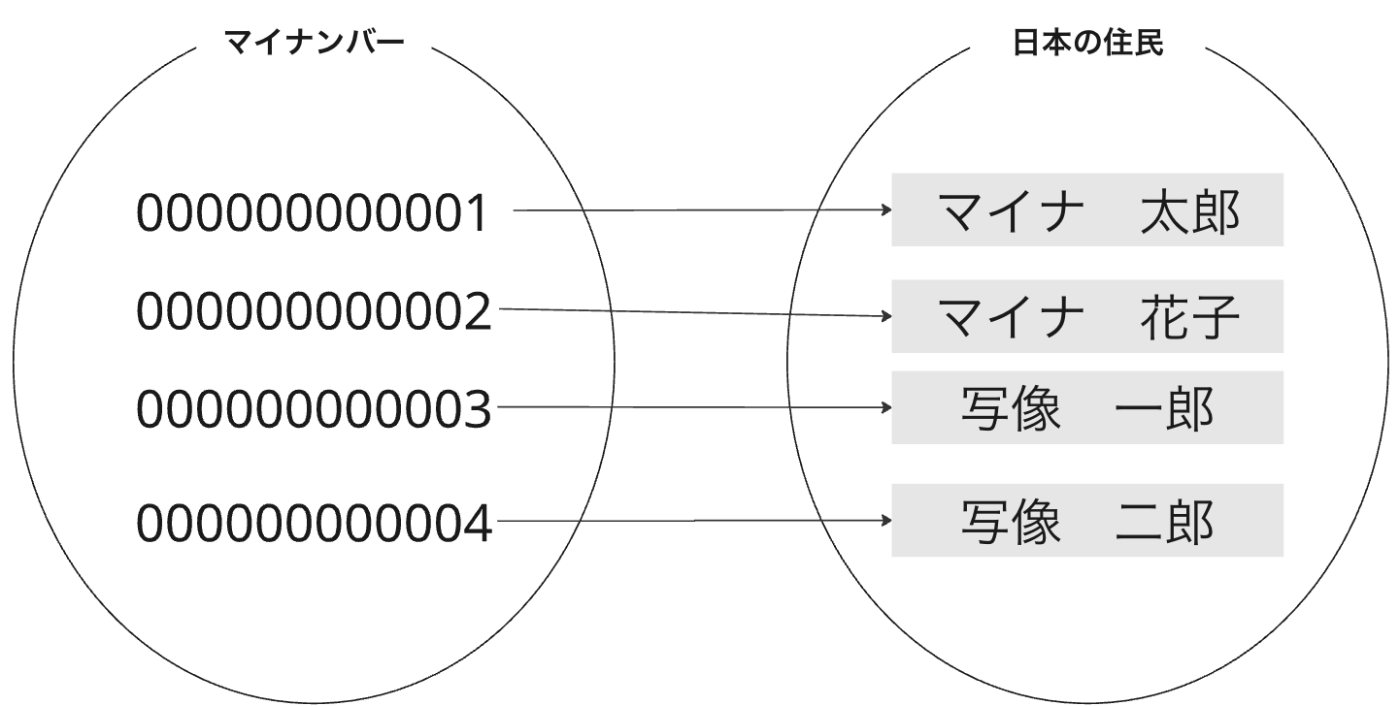
マイナンバーと日本の住民をの対応を考えます。マイナンバーは日本の全ての住民に割り当てられる12桁の個人識別番号であり、 全射 と 単射 の特性を兼ね備えた写像です。このような写像を全単射 と呼びます。
ソフトウェア開発と写像
ここからはソフトウェア開発に頭を戻し、写像の知識がどのようにソフトウェア技術の理解に活きるのかを見ていきます。写像の概念を交えながら、RDB(リレーショナルデータベース)の論理設計における 正規化(normalization) を見ていきましょう。
RDBの論理設計 〜第二正規化
以下のテーブルは、会社とその社員情報を管理するテーブルです。
| 会社コード(主キー) | 会社名 | 社員ID(主キー) | 社員名 |
|---|---|---|---|
| C001 | A商事 | 001 | 加藤 |
| C001 | A商事 | 002 | 藤本 |
| C001 | A商事 | 003 | 三島 |
| C002 | B科学 | 004 | 斉藤 |
| C002 | B科学 | 005 | 田島 |
| C002 | B科学 | 006 | 渋谷 |
このテーブルでは、社員名は複合主キー(社員ID・会社コード)に従属してますが、会社名は会社コードに従属しています。このように、主キーの一部に従属性がある関係を 部分関数従属性(partial functional dependency) と呼びます。
このテーブルには次の問題点があります。
- 社員IDが主キーなため、社員がいない会社をテーブルに登録できない。
- 社員IDと会社コードの複合主キーにため、{C001, A商事}, {C001,B科学}というレコードを登録できてしまう。
第二正規化では、部分関数従属性を解消し、完全関数従属性のみのテーブルに分解します。
| 会社コード(主キー) | 社員ID(主キー) | 社員名 |
|---|---|---|
| C001 | 001 | 加藤 |
| C001 | 002 | 藤本 |
| C001 | 003 | 三島 |
| C002 | 004 | 斉藤 |
| C002 | 005 | 田島 |
| C002 | 006 | 渋谷 |
| 会社コード(主キー) | 会社名 |
|---|---|
| C001 | A商事 |
| C002 | B科学 |
| C003 | C建設 |
これにより、社員のいない会社でもテーブルに登録できるようになり、会社コードの重複({C001, A商事}, {C001,B科学})といった不整合データの発生を抑制できました。
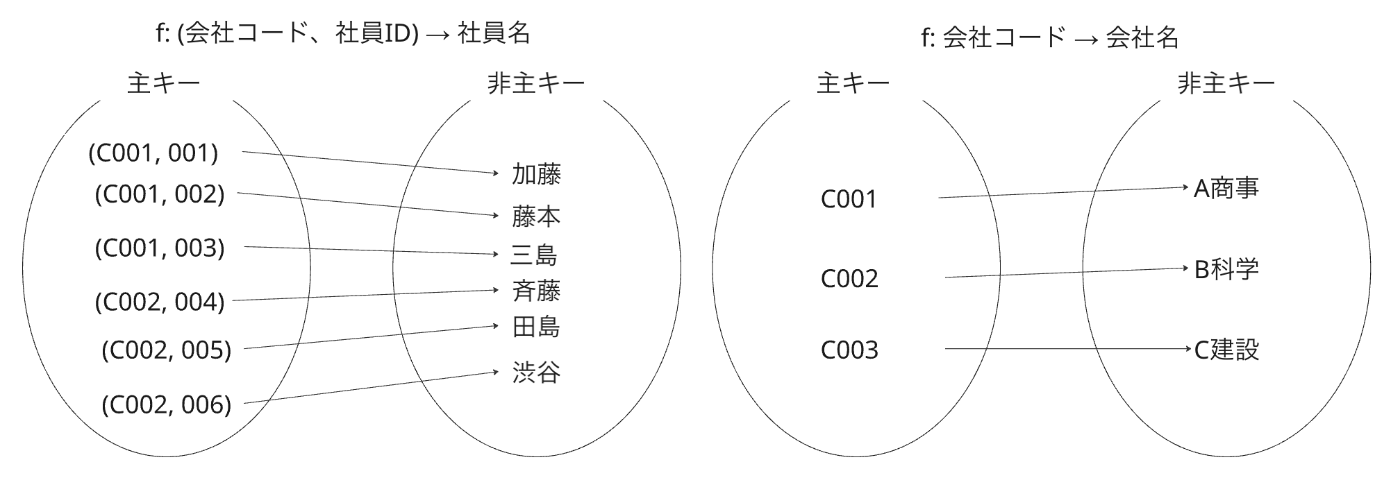
この第二正規化「部分関数従属性を解消し完全関数従属性のみのテーブルを作ること」を、数学的に言えば「主キーの集合 X と非主キー属性の集合 Y を対応する写像(f : X → Y)に変換する」と解釈できます。また、整合性が担保された主キー集合と非主キー属性の集合間を対応する写像は 全単射 であることがわかります。
数学的な視点で解釈できると何が嬉しいのか
正直、同僚にこの質問されて上手く答えられなかったです。なぜなら、ここで紹介した数学の知識がなくてもソフトウェア開発の現場で活躍は可能ですし、技術書もいちいち数式を持ち出して解説していることは少ないからです。
その上で、数学を学ぶ自分なりの答えは、「数学を学ぶことで、具体から抽出した抽象的な知識を、数式や図で見える化できること。また、その抽象的な知識を別の具体な事象に応用できること」 です。
ソフトウェアで言えば、開発手法や言語仕様は具体的な側面で、それらの本質となる原則や考え方は抽象的な側面です。前述のRDBの論理設計を写像を利用して解釈する経験は、また別のソフトウェア技術を学ぶ際に、具体の理解を助ける抽象として役立つはずです。
最後に
初歩的ではありますが、数学を学んだことで、プログラムの出入力を集合を捉えたり、テーブル設計の関数従属性を写像を交えて解釈するなど、ソフトウェア技術に新しい発見を見出すことができました。技術の本質的な部分の理解に目を瞑ることが、以前よりは減った気がします。
最後まで読んでいただき、ありがとうございました。少しでも皆さんのソフトウェア技術への視点に、新しい気づきをもたらすことができたなら幸いです。
Discussion