無限反復指数関数の定義域に関するメモ(Part 2)

無限反復指数関数の定義域に関するメモ(Part 1) の続きです
こんなに長くなるとは思いませんでしたので、また整理するかも...

前回のあらすじ

無限反復指数関数 $\mathcal{T}$ は部分写像であり、以下を満たすとします。

$$\begin{equation} \mathcal{T}:U \subset \mathbb{R}^+ \rightarrow V\subset \mathbb{R}^+; x \mapsto \mathcal{X} ~\text{s.t.}~ (\mathcal{X}=\lim_{n\to\infty}{^n{x}}, ~ \mathcal{X} \ll \infty) \end{equation}$$

このとき、$\mathcal{T}$ の定義域が $e^{-e}\le x \le e^{\frac{1}{e}}$ であること、すなわち

$$\begin{equation} \text{dom}\left(\mathcal{T}\right) = \{ x\in\mathbb{R}^+~|~ e^{-e}\le x \le e^{\frac{1}{e}} \} \end{equation}$$

を確かめたいです。

前回はこの上限が正しいこと、すなわち

$$\begin{equation} \sup \text{dom}(\mathcal{T})=e^{\frac{1}{e}} \end{equation}$$

および

$$\begin{equation} \{x\in \mathbb{R}^+~|~1\le x \le e^{\frac{1}{e}}\} \subset \text{dom}(\mathcal{T}) \end{equation}$$

を確認しました。

今回確認したいこと

$\mathcal{T}$ の定義域の下限が $e^{-e}$ であることを確認します。すなわち

$$\inf \text{dom}(\mathcal{T}) = e^{-e}$$

と

$$\{x\in \mathbb{R}^+~|~e^{-e} \le x \lt 1 \} \subset \text{dom}(\mathcal{T})$$

を確認し、最終的に(2)が正しいことを確認します。

---

表記

反復指数関数表記

以降において $\color{#FF0000}\exp_{a}^{n}(x)$ という表記を使用します。

• $n$階建ての$x$の上に、$a$が乗っている、すなわち$\underbrace{x^{x^{x^{^{\cdot^{\cdot^{\cdot^{a}}}}}}}}_{\text{height:}~n+1}$ を $\displaystyle \exp_{x}^{n}(a)$ と表記します
  • $n=0$ のときは $x$ の値に関わらず $a$ とします。つまり $\exp_x^0(a)=a$ です。
  • $n=1$ のときは $1$ は省略することがあります。つまり $\exp_x^1(a)$ と書くかわりに $\exp_x(a)$ と書くことがあります。

また、文脈に応じて $^nx$ を $\exp_{x}^{n}{(1)}$ または $\exp_{x}^{n-1}(x)$ のように書き分ける場合があります。

大小関係の表記

実数 $a, b, x$ について、 $\color{#FF0000}a \gtrless x \gtrless b$ は以下のように定義します:

• $a \lt x \lt b$ または $a \gt x \gt b$ のうち、いずれか1つが成り立つ

微分表記

前回に続き、関数の後ろに続く「$\color{#FF0000}'$」は微分を表します。

つまり、関数 $f(\chi)$ の $\chi$ による微分を $f'$ のように書きます。

単調写像

関数の 広義単調減少 または 広義単調増加 については、単に 単調減少 または 単調増加 と表記します。

---

方針の模索

実は上限を確認したときと同じようにグラフを使って考えようとすると、うまく行きません。

グラフ $y=x^{\frac{1}{x}}$ は、$x>0$ において常に正であり、かつ $\displaystyle \lim_{x \to \plusmn\infty}{f(x)} = 0$ が成り立つので、逆関数 $f^{-1}(x)$ の定義域に $x>0$ が含まれることはたやすく確認できます。

では、 $\mathcal{T}$ の定義域が $(0, 1]$ を含むのでしょうか？

実はこれは数値計算をしてみると、ある事実がわかります。

数値計算とプロット

これ以降、特に注釈がない限り、$x$ は $0 \lt x \lt 1$ を満たす実数とします。

以下のような数列 $T_n$ を考えてみましょう。

$$\begin{equation} \begin{aligned} T_0&=1 \\ T_1&=x \\ T_{n+1}&=x^{T_n} \end{aligned} \end{equation}$$

この $T_n$ の値を n-Tn 平面にプロットしてみましょう。

グラフ0:n-Tnの関係 for (0,1]

ここでは

• 横軸が $n~(2\le n \le 200)$^[1]
• 縦軸が $T_n$
• $x\in\{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 ,0.9 \}$
  • $x$ は $0.1$ に近づくほど赤く、$0.9$ に近づくほど紫色

としてプロットしてみましょう。

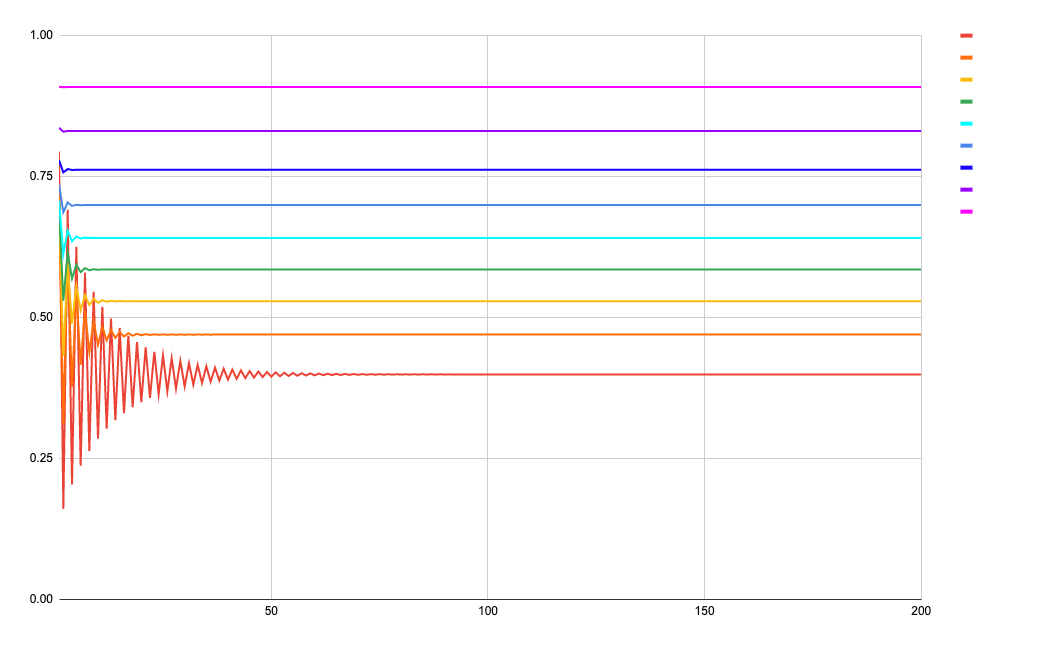
この図を見る限り、区間 $0.1 \le x \le 1$ においては値が収束しそうです。
そこで、次は区間 $0.01 \le x \le 0.1$ をクローズアップしてみます。

グラフ1:n-Tnの関係 for (0, 0.1]

ここでは

• 横軸が $n~(2\le n \le 200)$^[1:1]
• 縦軸が $T_n$
• $x\in\{0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08 ,0.09 \}$
  • $x$ は $0.01$ に近づくほど赤く、$0.09$ に近づくほど紫色

になるようにしました。

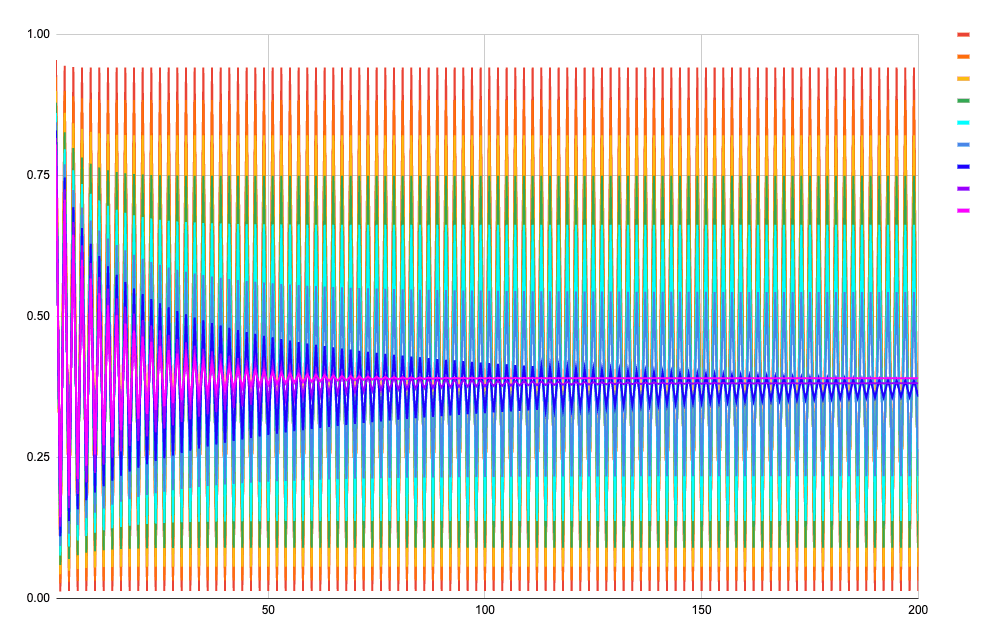
少々分かりづらいので、 $180 \le n \le 200$ の部分を拡大してみましょう。

グラフ2:n-Tnの関係(n=180~200) for (0, 0.1]

• 横軸が $n~(180\le n \le 200)$
• 縦軸が $T_n$
• $x\in\{0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08 ,0.09 \}$
  • $x$ は $0.01$ に近づくほど赤く、$0.09$ に近づくほど紫色

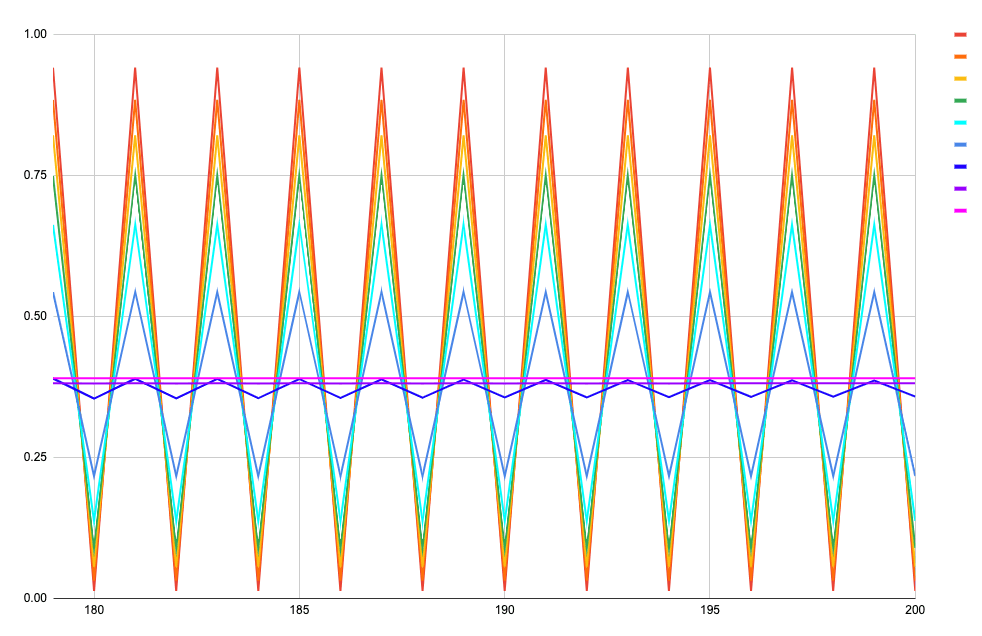
明らかに、$0.01$ に近づくほど上下に激しく揺れ、$0.9$ に近づくほど揺れがなくなっていきます。
違いをさらにはっきりさせるため、今度は $T_n$ の階差数列の絶対値をとってみましょう。

グラフ3:n-{Tnの階差数列の絶対値}の関係 for (0, 0.1]

• 横軸が $n~(2\le n \le 200)$^[1:2]
• 縦軸が $T_n$ の階差数列の絶対値
• $x\in\{0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08 ,0.09 \}$
  • $x$ は $0.01$ に近づくほど赤く、$0.09$ に近づくほど紫色

とすると、以下のようになります。

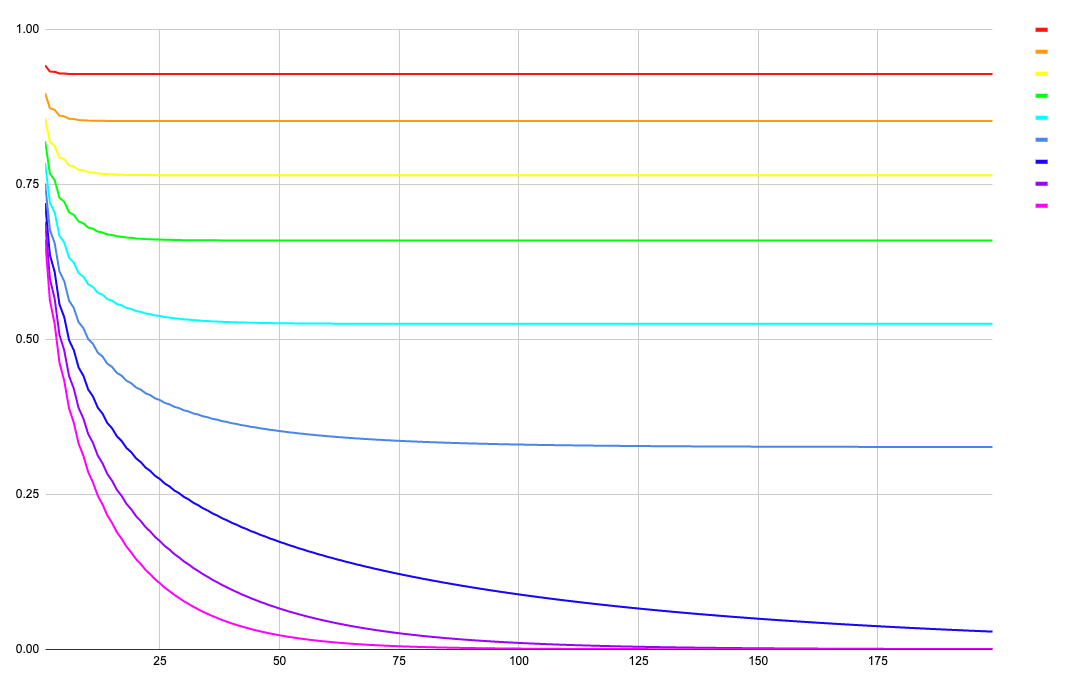
これらの事実から、少なくとも $0 \lt x \le 0.06$ において、 $\displaystyle \lim_{n \to \infty}{T_n}$ が振動するため、極限が存在しない ことを意味します。

よって、この事実と(5)から、ある実数 $\mathcal{L}~(0\lt \mathcal{L} \le 1)$ が存在し、

$$\begin{equation} \inf \text{dom}(\mathcal{T}) = \mathcal{L} \end{equation}$$

が成り立つことが推測されます。

方針の列挙と選定

それでは、(6) における $\mathcal{L}$ をどのように求めたらよいでしょうか。
数値計算であれば、精度を決めた上で二分探索して近い値をWolfram Alphaで探す、なんて手法はとれそうですが、なるべくなら厳密解を求めたいです。

方針候補1: ダランベールの収束判定法から条件をひねり出す？

ダランベールの収束判定法を利用して、 $\mathcal{L}$ を探し出す手がかりがつかめないか、試してみましょう。
十分大きな $n$ において、隣り合う二項間の商 $T_{n+1}/T_n$ が収束する気配を見せるのであれば、もしかしたら手がかりになるかもしれません。
ただし、$T_n$ が振動しているという事実があるので、$T_{n+2}/T_{n+1}$ と $T_{n+1}/T_n$ を計算してみることにします。

ということで、以下のような数値計算を試します。

$1000000$ が十分大きいのかという疑問はありますが、限界である小数以下18桁に収めることを考えれば十分な気がしたので、いったんこれで様子をみた感じです

Swift

import Foundation

func calc(x: Double) -> Double { calc(x: x, loop: 1000000) }
func calc(x: Double, loop: Int) -> Double {
    var buf = x
    for _ in 0..<loop {
        buf = pow(x, buf)
    }
    return buf
}

for i in (1..<10).map({ a -> Double in Double(a) / 100.0 }) {
    let v1 = calc(x: i, loop: 1000000)
    let v2 = calc(x: i, loop: 1000001)
    let v3 = calc(x: i, loop: 1000002)
    print("商1:", abs(v2/v1))
    print("商2:", abs(v3/v2))
    print("---")
}

結果は以下のとおりです。
商1が $T_{n+1}/T_n$ で、商2が $T_{n+2}/T_{n+1}$ です。

output

商1: 71.91039861275924
商2: 0.013906194643490234
---
商1: 28.103957967711207
商2: 0.035582176757768626
---
商1: 14.631818202752074
商2: 0.06834420617746001
---
商1: 8.364332988120232
商2: 0.11955525938772268
---
商1: 4.824284755625473
商2: 0.20728461329608
---
商1: 2.5045383910719576
商2: 0.39927517324739187
---
商1: 1.0000000000000007
商2: 0.9999999999999994
---
商1: 1.0000000000000007
商2: 0.9999999999999994
---
商1: 1.0000000000000009
商2: 0.9999999999999991
---

ある地点から急に収束の兆しを見せています。
それはいいのですが、最大の問題は $1$に収束しようとしている兆しがある ところです。
ダランベールの収束判定法では、(5)のもとで $\displaystyle \lim_{n\to\infty}{\frac{T_{n+1}}{T_n}}$ が $1$ に収束してしまうと、収束判定ができません。

この方針はうまくいかなそうです。

方針候補2: 階差数列の絶対値が0に収束するかもしれない現象を利用する？

あらためて、前述のグラフ3を観察してみましょう。
このグラフは $T_n$ の階差数列の絶対値をプロットしたものでした。
この数列を $U$ とおき、きちんと定義してみます。

$$\begin{aligned} U_0&=|T_1-T_0|=|x^x - x|=|x(x^{x-1}-1)|\\ U_{n+1}&=|T_{n+1}-T_n|=|^{n+1}x-^nx|=\left| \underbrace{x^{x^{x^{^{\cdot^{\cdot^{\cdot}}}}}}}_{\text{height:}~n+1} - \underbrace{x^{x^{x^{^{\cdot^{\cdot^{\cdot}}}}}}}_{\text{height:}~n} \right|\\ \end{aligned}$$

...なんですが、 これを手で計算できるかと言われると難しそうです^[2]。
別の方法を探しましょう。

方針候補3: 引数と極限値の関係式を作ったら手がかりになりそう？

前回、上限を求める際に、引数 $a$ と $\mathcal{T}(a)$ の極限値 $c$ を用いて、$c=a^c$ という関係式をつくりました。

これと同じ方法で関係式を作って、手がかりをつかめないでしょうか？

(5)およびその値のグラフを見る限り、$T_n$ は常に収束しないようにみえます。
しかし、ここでもう一度グラフ1を観察してみましょう。

なんとなく、$T_n$ の揺れの上限と下限は一定値に収束しているように見えないでしょうか？

そこで、上辺と下辺の点たちを表す数列をそれぞれ（計２つ）考え、それらの収束を観察すると、なんとなくヒントが得られる気がしてきます^[2:1]。

この方針で考えてみましょう。

考察

実数の数列 $H_{n}$ および $L_{n}$ が存在し、「$T_n$の揺れ」の上限を左から順に$H_1, H_1,...$に、下限を順に $L_1, L_2, ...$ と対応付けて様子をみることにしましょう。

以下のように定義します。

$$\begin{equation} \begin{aligned} L_1 = x&, ~~L_{n+1}= x^{x^{L_n}}= T_{2n-1} \\ H_1 = x^x&, ~~H_{n+1}= x^{x^{H_n}}= T_{2n} \end{aligned} \end{equation}$$

ただし、区間 $0 \lt x \lt 1$ において $x \lt x^x$ かつ $x^x > x^{x^x}$ であることに注意です。

指数関数の性質により、$0 \lt a \lt 1$ のとき $s > t \Rightarrow a^s < a^t$ です。
よって、区間 $0 \lt x \lt 1$ において $x=x^1$ に注意すると $x < x^x$ です。
同様に、区間 $0 \lt x \lt 1$ において $x < x^x \Rightarrow x^{x} > x^{x^{x}}$ がなりたちます。

さて、この条件のもとで、ある実数 $L_{\infty}$ と $H_{\infty}$ が存在し、それぞれ $L_n$、$H_n$ の極限値と一致するとします。つまり、

$$\begin{equation} \begin{aligned} \lim_{n \to \infty}{L_n} &= L_{\infty} \\ \lim_{n \to \infty}{H_n} &= H_{\infty} \end{aligned} \end{equation}$$

を満たすとします。

このとき、$x$ と $L_{\infty},~H_{\infty}$ の関係を調べていくと、何かわかるかもしれません。

極限の存在確認

その前に、あやふやにしていた事実をいくつか確認しないといけません。

極限 $L_{\infty},~H_{\infty}$ は本当に存在するのでしょうか？

前掲のグラフから「なんとなく収束しそう、なんとなく極限がありそう」といった曖昧な議論が続いていて、あまりよろしくありません。
そこで、$L_n$ と $H_n$ の極限についてきちんと見ていきましょう。

ゴールの設定

いったん、$L_{\infty},~H_{\infty}$ を忘れることにしましょう。

前掲のグラフ1を観察すると、上辺と下辺の点たちはだんだん中央に向かっていくように見えます。
よって、(7)の定義のもと、以下の仮説を思いつくことができます。

$$\begin{equation} \begin{aligned} 1 > H_1 > H_2 > H_3 > ... > 0 \\ 0 < L_1 < L_2 < L_3 < ... < 1 \end{aligned} \end{equation}$$

これが正しいかを確認します。

Tの2項間の観察

(9)について、単調減少または単調増加であることを確認する方法として、隣り合う二項の違いを観察するのは有効そうです。

ただ、$L_n$ と $H_n$ については冪乗の形式で定義されていることから、二項間の差を観察しようとしても、そもそも計算ができずに詰んでしまいそうです。

そこで、差の代わりに隣り合う二項間の商、つまり、$L_{n+1}/L_n$ や $H_{n+1}/H_n$ を観察しましょう。

とはいえ、 $L_n$ と $H_n$ はいずれも「数列 $T_n$ の一つ飛び」で値を抜き出しているので、$T_n$ たちの関係をうまく整理できていない場合、計算が行き詰まるかもしれません。

$L_{n}$ たちの関係を整理したいのに、該当する $T_n$ がどれかわからない、なんてことが起きるともうどうにもなりません。

なので、余裕を持って式変形できるように $T_n$ に関する 四項間漸化式 を用意します。

「二項間漸化式の一つ飛び、ということは、その2倍の四項間漸化式を考えれば十分だろう」という安易な発想によるものです。

すると、(5)より $T_{n+2}=x^{T_{n+1}}$ かつ $T_{n+1}=x^{T_{n}}$ であることから

$$\begin{aligned} T_{n+2} &= x^{x^{T_n}} \\ &= x^{x^{T_n} - T_n + T_n}\\ &= x^{x^{T_n} - T_n} \cdot x^{T_n} \\ &= x^{T_{n+1} - T_n} \cdot T_{n+1} \end{aligned}$$

整理して

$$\begin{equation} \begin{aligned} \frac{T_{n+2}}{T_{n+1}} = x^{T_{n+1} - T_n} \end{aligned} \end{equation}$$

という感じで、三項間漸化式の形に無理やり変形しました。
さらに $T_{n+3}$ を同じように考えることで

$$\begin{equation} \begin{aligned} \frac{T_{n+3}}{T_{n+2}} = x^{T_{n+2} - T_{n+1}} \end{aligned} \end{equation}$$

がいえます。

ここで 式(11) × 式(10) を計算すると

$$\begin{aligned} \frac{T_{n+3}}{T_{n+2}} \cdot \frac{T_{n+2}}{T_{n+1}} &= x^{T_{n+2} - T_{n+1}} \cdot x^{T_{n+1} - T_n} \\ \frac{T_{n+3}}{T_{n+1}} &= x^{T_{n+2} - T_{n+1}+T_{n+1} - T_n}\\ &= x^{T_{n+2} - T_n} \end{aligned}$$

$$\begin{equation} \begin{aligned} \therefore \frac{T_{n+3}}{T_{n+1}} = x^{T_{n+2} - T_n} \end{aligned} \end{equation}$$

という四項間漸化式ができあがります。

H,Lの2項間の関係

(12)を使って、$L_n$ と $H_n$ の「隣り合う二項間の関係」を見てみましょう。
一部、べき乗表記が見づらくなるので、かわりに(5)の $T_n$ を使用して表現します。

(7)より $L_n$ について、(12)を用いて整理すると

$$\begin{equation} \begin{aligned} \frac{L_2}{L_1} &= \frac{x^{x^x}}{x} = x^{\left(x^{x}-1\right)}=\exp_x({T_{2}-T_{0})} \\ \frac{L_3}{L_2} &= \frac{x^{x^{x^{x^x}}}}{x^{x^x}}=x^{\left(\left(x^{x^{x^{x}}}\right)-\left(x^x\right)\right)}=\exp_x({T_{4}-T_{2}}) \\ \vdots \\ \frac{L_{n+1}}{L_{n}} &= \frac{T_{2n+1}}{T_{2n-1}}=\exp_x{(T_{2n}-T_{2n-2})} \end{aligned} \end{equation}$$

また、$H_n$ については

$$\begin{equation} \begin{aligned} \frac{H_2}{H_1} &= \frac{x^{x^{x^x}}}{x^x} = x^{\left(x^{x^{x}}-x\right)}=\exp_x({T_{3}-T_{1}}) \\ \frac{H_3}{H_2} &= \frac{x^{x^{x^{x^{x^x}}}}}{x^{x^{x^x}}}=x^{\left(\left(x^{x^{x^{x^{x}}}}\right)-\left(x^{x^x}\right)\right)}=\exp_x({T_{5}-T_{3}}) \\ \vdots \\ \frac{H_{n+1}}{H_{n}} &= \frac{T_{2n+2}}{T_{2n}}=\exp_x{(T_{2n+1}-T_{2n-1})} \end{aligned} \end{equation}$$

という関係が、それぞれわかります。

もし、この関係から

• $\displaystyle \frac{L_{n+1}}{L_{n}}$ と $1$ との大小関係
• $\displaystyle \frac{H_{n+1}}{H_{n}}$ と $1$ との大小関係

がわかれば、(9)の証明に繋げられそうです。

補題1

ここで、実数の冪乗の大小関係に関する次の補題を証明しておきます。

$$\begin{aligned} \forall \alpha \in \mathbb{R}~~\text{s.t.}~~\alpha\ne 0, \forall \beta \in \mathbb{R} ~~\text{s.t.}~~ 0 \lt \beta \lt 1,~~ \begin{cases} \alpha \gt 0 &\Rightarrow~ \beta^{\alpha} \lt 1\\ \alpha \lt 0 &\Rightarrow~ \beta^{\alpha} \gt 1 \end{cases} \end{aligned}$$

$\forall \alpha \in \mathbb{R}$ は「任意の実数 $\alpha$」の意味であり、$\text{s.t.}$ は such that の略です。

証明

$\alpha$ が正の実数である場合

$1$ より大きい実数 $r$ を用いて $\displaystyle \beta=\frac{1}{r}$ とおくと、

$$\beta^{\alpha} = \left(\frac{1}{r}\right)^{\alpha}=\frac{1}{r^{\alpha}}$$

ここで $\displaystyle \frac{1}{r^{\alpha}}=e^{\log{\frac{1}{r^{\alpha}}}}$ であることに注意すると

$$\begin{aligned} \frac{\text{d}}{\text{d}\alpha}\left(\frac{1}{r^{\alpha}}\right)&=\frac{1}{r^{\alpha}}\log{\frac{1}{r}}\\ &=\frac{1}{r^{\alpha}}\log{r^{-1}}\\ &=-\frac{1}{r^{\alpha}}\log{r} \end{aligned}$$

$r>0,\alpha>0$ だったので、$\displaystyle \frac{\text{d}}{\text{d}\alpha}\left(\frac{1}{r^{\alpha}}\right) < 0$ となり、$\displaystyle \frac{1}{r^{\alpha}}$ は単調減少関数とわかります。

よって、$r^0=1$ から $\displaystyle \frac{1}{r^{\alpha}} < 1$ が従い、結果として

$$\beta^\alpha \lt 1$$

が成り立ちます。（証明終）

$\alpha$ が負の実数である場合

$1$ より大きい実数 $r$ と 正の実数 $s$ を用いて

$$\alpha=-s,~~\beta=\frac{1}{r}$$

とおくと、

$$\beta^{\alpha} = \left(\frac{1}{r}\right)^{-s}=r^s$$

ここで $\displaystyle r^s=e^{\log{r^s}}$ であることに注意すると

$$\begin{aligned} \frac{\text{d}}{\text{d}s}r^{s}&=r^{s}\log{r} \end{aligned}$$

$r>0,s>1$ だったので、$\displaystyle \frac{\text{d}}{\text{d}s}r^{s} > 0$ となり、$r^s$ は単調増加関数とわかります。

よって、$r^0=1$ から $r^s>1$ が従い、結果として

$$\beta^\alpha \gt 1$$

が成り立ちます。（証明終）

小さな添字で観察

ところで、区間 $0 \lt x \lt 1$ においては $x^x \lt 1$ なので、明らかに

$$\begin{equation} x^x - 1 = T_{2}-T_{0} \lt 0 \end{equation}$$

です。

ゆえに、(13)において 補題1 より

$$\begin{equation} \exp_x(T_{2}-T_{0}) \gt 1 \end{equation}$$

となるため

$$\begin{equation} \frac{L_2}{L_1} \gt 1 \end{equation}$$

が成り立ちます。

同様に、(15)(16)から $x^x-1 \lt 0 ~\Rightarrow~x^{(x^x-1)}-1 \gt 0$ が言えますので

$$\begin{equation} x^{x^x}-x=x^{\left(x^{(x^x-1)}-1\right)} \gt 0 \end{equation}$$

が成り立ち、ゆえに(14)において 補題1 より

$$\begin{equation} \exp_x(T_{3}-T_{1})\lt 1 \end{equation}$$

となるため

$$\begin{equation} \frac{H_2}{H_1} \lt 1 \end{equation}$$

が成り立ちます。

数学的帰納法

さて、(17)と(20)を用いて

• $\displaystyle \frac{L_{n+1}}{L_{n}}$ と $1$ との大小関係
• $\displaystyle \frac{H_{n+1}}{H_{n}}$ と $1$ との大小関係

を求めたいのですが、ここで数学的帰納法が使用できないか、試してみます。

$1$より大きい自然数$k$があるとき、$n=k$ において

$$\begin{equation} \begin{aligned} \frac{L_{k+1}}{L_{k}} = \frac{T_{2n+1}}{T_{2n-1}}=\exp_x(T_{2n}-T_{2n-2}) &\gt 1\\ \end{aligned} \end{equation}$$

$$\begin{equation} \begin{aligned} \frac{H_{k+1}}{H_{k}} = \frac{T_{2n+2}}{T_{2n}}=\exp_x(T_{2n+1}-T_{2n-1}) &\lt 1 \end{aligned} \end{equation}$$

であると仮定します。
すると、$n=k+1$ のとき

$$\begin{equation} \begin{aligned} \frac{L_{k+2}}{L_{k+1}}&=\frac{T_{2n+3}}{T_{2n+1}}=\exp_x(T_{2n+2}-T_{2n}) \end{aligned} \end{equation}$$

$$\begin{equation} \begin{aligned} \frac{H_{k+2}}{H_{k+1}}&=\frac{T_{2n+4}}{T_{2n+2}}=\exp_x(T_{2n+3}-T_{2n+1}) \end{aligned} \end{equation}$$

となりますが、ここで (22) より

$$\frac{T_{2n+2}}{T_{2n}} \lt 1 ~~\Rightarrow~~T_{2n+2} \lt T_{2n}$$

なので、補題1 より

$$\begin{equation} T_{2n+2} - T_{2n} \lt 0~~\Rightarrow~~\exp_x(T_{2n+2}-T_{2n}) \gt 1 \end{equation}$$

すなわち(23)から

$$\begin{equation} \frac{L_{k+2}}{L_{k+1}}=\frac{T_{2n+3}}{T_{2n+1}}=\exp_x(T_{2n+2}-T_{2n}) \gt 1 \end{equation}$$

であることがわかりました。

さらに、この(26)の結果から

$$\frac{T_{2n+3}}{T_{2n+1}} \gt 1 ~~\Rightarrow~~T_{2n+3} \gt T_{2n+1}$$

なので、 補題1 より

$$\begin{equation} T_{2n+3} - T_{2n+1} \gt 0~~\Rightarrow~~\exp_x(T_{2n+3}-T_{2n+1}) \lt 1 \end{equation}$$

すなわち(24)から

$$\begin{equation} \frac{H_{k+2}}{H_{k+1}}=\frac{T_{2n+4}}{T_{2n+2}}=\exp_x(T_{2n+3}-T_{2n+1}) \lt 1 \end{equation}$$

であることがわかりました。

よって、数学的帰納法を用いると

• (17)(21)(26)より $\displaystyle \frac{L_{n+1}}{L_{n}} \gt 1$
• (20)(22)(28)より $\displaystyle \frac{H_{n+1}}{H_{n}} \lt 1$

がそれぞれ成り立ち、結果として(9)が従います。

２つの極限値

(9)より、数列 $L_n$ は単調増加し、$H_n$ は単調減少しますが、区間 $(0, 1)$ を脱出することができないので、この区間のとこかの値に収束しなければならないはずです。

よって、それらを改めて $L_{\infty}$ と $H_{\infty}$ とし、それぞれ $L_n$、$H_n$ の極限値と一致するとします。
要は(8)の定義そのものなのですが、再掲すると以下のようなものです。

$$\begin{aligned} \lim_{n \to \infty}{L_n} &= L_{\infty} \\ \lim_{n \to \infty}{H_n} &= H_{\infty} \end{aligned}$$

ここで、もう一度グラフ1を見てみましょう。

$x$ が増加するとともに振幅が小さくなっていくのがわかります。
これはすなわち $L_n$ と $H_n$ の極限が近づいていくことを示しているのですが、ここで長らく忘れていた $\mathcal{T}$ を思い出してください。

• $x=0.01$ のとき $\displaystyle \lim_{n\to\infty}{^nx}$ は発散（振動）
• $x=1$のとき $\displaystyle \lim_{n\to\infty}{^nx}$ は収束

であったので、(1) の定義から、$x$ を限りなく $0$ に近い点から徐々に増やしたときに、 $L_{\infty}$ と $H_{\infty}$ が一致するような $x$ (それを $x_0$ とします)が見つかれば、それこそが $\mathcal{L}$ であることがわかります。

つまり、$L_{\infty}$ と $H_{\infty}$ が $x$ に依存する値であることに注意して

$$\begin{equation} \min \{~ x ~|~ L_{\infty} = H_{\infty} \} \overset{\text{def}}{=} x_0 ~~\Rightarrow~~ \inf \text{dom}(\mathcal{T}) = x_0 =\mathcal{L} \end{equation}$$

が言えます。

境界値の計算へ

さて、いよいよ境界値 $\mathcal{L}$ を求めていきたいのですが、何を手がかりにすれば良いかがよくわかりません。
いま、わかっているのは(5)の

$$T_{n+1} = x^{T_n}$$

と、これの派生である (7) だけです。

なので、(5)や(7)をいろいろなカタチに変形して観察してみましょう。

漸化式の観察

$L$ についての漸化式 (7)

$$L_{n+1}=x^{x^{L_n}}$$

について、(9)より真数条件を満たすことに注意し、両辺の対数をとります。すると

$$\begin{equation} \begin{aligned} \log{L_{n+1}}=x^{L_n}\log{x} \end{aligned} \end{equation}$$

ここでさらに、(9)とグラフ0およびグラフ1から $0 \lt T_n \lt 1$ であることに注意し、もう一度両辺の対数をとると

$$\begin{equation} \begin{aligned} \log\log{L_{n+1}}=L_n\log{x} + \log\log{x} \end{aligned} \end{equation}$$

になります。

ネタバレ

お気づきの方もいらっしゃるかと思いますが、この式変形は誤りです。
正しい内容だけ知りたい方は「境界値の計算へ（やりなおし)」まで飛ばしてください。

数列 $H$ も同じように2回対数をとると

$$\begin{equation} \begin{aligned} \log\log{H_{n+1}}=H_n\log{x} + \log\log{x} \end{aligned} \end{equation}$$

となります。

ところで、(8)より、この2つの式はそれぞれ

$$\begin{equation} \begin{aligned} \log\log{L_{\infty}}=L_{\infty}\log{x} + \log\log{x} \end{aligned} \end{equation}$$

$$\begin{equation} \begin{aligned} \log\log{H_{\infty}}=H_{\infty}\log{x} + \log\log{x} \end{aligned} \end{equation}$$

が成り立つはずです。

そして、(29)より、もし $L_{\infty}=H_{\infty}=\mathcal{T}(\mathcal{L})$ であるなら

$$\begin{equation} \begin{aligned} \log\log{\mathcal{T}(\mathcal{L})}=\mathcal{T}(\mathcal{L})\log{x} + \log\log{x} \end{aligned} \end{equation}$$

が成り立たなければなりません。

これを変形していきたいのですが、式に $\log\log$ があってちょっと扱いづらそうです。よって $u=\log{\mathcal{T}(\mathcal{L})}$ として式を変形します。
（この定義により $e^u=\mathcal{T}(\mathcal{L})$ となることに注意してください。）

$$\begin{equation} \begin{aligned} \log{u}=e^u\log{x} + \log\log{x} \end{aligned} \end{equation}$$

さらに $x$ を一旦定数として固定しましょう。$C=\log{x}, ~D=\log\log{x}$ とすると

$$\begin{equation} \begin{aligned} \log{u}=e^uC + D \end{aligned} \end{equation}$$

となります。

解の存在

この式を使って、$u$ が解を持つ条件を見ていきます。
項をまとめて右辺に移動して $0=...$ のカタチにしてから、これを関数 $g(u)$ とすると

$$\begin{equation} \begin{aligned} g(u)=e^uC + D - \log{u} \end{aligned} \end{equation}$$

ここで $g(u)$ を $u$ で微分すると

$$\begin{equation} \begin{aligned} g'(u)&=e^uC - \frac{1}{u} \end{aligned} \end{equation}$$

となります。

ここで、$0 \lt C = \log x \lt 1$ に注意しながら (39)をよく観察すると

$$\begin{equation} \begin{aligned} \lim_{u \to +0}{e^uC}=1,~~\lim_{u \to +0}{-\frac{1}{u}}=-\infty\\ \therefore \lim_{u \to +0}{\left(e^uC - \frac{1}{u}\right)}=1-\infty=-\infty \end{aligned} \end{equation}$$

かつ

$$\begin{equation} \begin{aligned} \lim_{u \to \infty}{e^uC}=\infty,~~\lim_{u \to \infty}{-\frac{1}{u}}=0\\ \therefore \lim_{u \to +0}{\left(e^uC - \frac{1}{u}\right)}=\infty-0=\infty \end{aligned} \end{equation}$$

であることがわかります。

よって、中間値の定理から $g'(u)=0$ となる $u$ が 1つ以上 存在することがわかります。

さらに(39)から

$$\begin{aligned} g''(u) = e^x+\frac{1}{x^2} \end{aligned}$$

なのですが、これは明らかに $u>0$ において $g''(u)>0$ です。

従って、$g'(u)$ は $u > 0$ において単調増加しますので、中間値の定理と合わせると、$g'(u)=0$ となる $u$ が 1つだけ 存在することがわかります。
この事実と、(40)と(41)から、$g'(u)$ は $u=0$ の前後で符号がマイナスからプラスに変化することがわかります。

以上から、$g(u)$ のグラフについて増減表を書くと次のようになります。

$u$	$(0)$	$...$	$?$	$...$	$(\infty)$
$g'(u)$	$(-\infty)$	$-$	$0$	$+$	$(\infty)$
$g''(u)$	$(\infty)$	$\cap$	$?$	$\cap$	$(\infty)$
$g(u)$	$(\infty)$	$\searrow$	$?$	$\nearrow$	$(\infty)$

$g(u)$の形がおおまかに見えてきました。しかしまだまだ情報不足ですので、$g'(u)$ についてもう少し観察してみましょう。

謎の関数W

(39) より

$$\begin{aligned} g'(u)=0 \Rightarrow e^uC = \frac{1}{u} \end{aligned}$$

$0 \lt x \lt 1$ および (36)(37)から、$C > 0$ なので、両辺をCで割ることができます。
よって両辺に $u/C$ をかけると

$$\begin{aligned} e^uC = \frac{1}{u} \Leftrightarrow ue^u=C^{-1} \end{aligned}$$

ここで $c=C^{-1}$ とおくと

$$\begin{equation} \begin{aligned} c=ue^u \end{aligned} \end{equation}$$

と書けます。この式を観察してみましょう。

目的は $g'(u)=0$ を満たす $u$ の値を知ることでしたので、$u=$ナントカ の形に整理して様子をみます。
関数 $f(x)=ue^{u}$ の逆関数を$W$ とします。つまり

$$W^{-1}(u)=ue^{u}$$

です。
この式から何がわかるでしょうか？

...
...

何もわかりませんでした😭

$W$を初等的に書き表す方法が見つからないので、詰みました。

---

なにかがおかしい

袋小路に入ってしまったら「戻る」が定石です。

なにか見落としていること、忘れていることはないでしょうか？
一歩定義に立ち戻って考えてみましょう。

(6)と(29)により $0 \lt \mathcal{L} \lt 1$ であり、(35)(36) から $u=\log{\mathcal{T}(\mathcal{L})}$ でした。
よって (9) と (29)、そして $0 \lt \alpha \lt 1 \Rightarrow \log{\alpha} \lt 0$ に注意すると

$$\begin{equation} \begin{aligned} u=\log{\mathcal{T}(\mathcal{L})} \lt 0 \end{aligned} \end{equation}$$

という関係が浮かび上がります。

そういえば...(31)以降の式変形で、この条件を特に考慮していませんでしたね...

正だと思っていた数が実は負だった、という展開のときは、たいてい何かを見落としていたりします。
これまでの式変形のどこかが間違っていてもおかしくはないですね...

矛盾

というか、実際にやらかしていて (30)から(31)への式変形 がまさにそれです。
$\log{x}$ の真数条件が $x > 0$ なので、 $\log\log{x}$ の真数条件は $\log{x} > 0$ になります。

そのため、$\log\log{x}$の定義域は、$x > 1 \Rightarrow \log{x} > 0$ に注意すると

$$\text{dom}(\log\log{x}) = \{x\in \mathbb{R}~|~1\lt x\}$$

でなければならないはずですが、これは冒頭の定義 $0<x<1$ とバッチリ矛盾します。
つまり、(30)から(31)への式変形 は不可能です。

境界値の計算へ（やりなおし)

ということで、元凶となっている「対数をとった場所」である(30)からやり直してみましょう。

安全策

両辺が1より小さいため、対数をとった時点で両辺が負になることがわかります。
ただ、そのまま計算すると、上のようにケアレスミスしてしまうかもしれません...。

なので、これを無理やり正に補正して、事故が起きないようにします。
そのためには両辺を $-1$ 倍すればよいです。すなわち

$$\begin{equation} \begin{aligned} \log{L_{n+1}}=x^{L_n}\log{x} \end{aligned} \end{equation}$$

の両辺を $-1$ 倍して

$$\begin{equation} \begin{aligned} -1\cdot\log{L_{n+1}}&=-1\cdot x^{L_n}\log{x}\\ \therefore~ \log{\frac{1}{L_{n+1}}}&= x^{L_n}\log{\frac{1}{x}} \end{aligned} \end{equation}$$

とします。
これでマイナス値を恐れる必要が（割と）なくなりますね。

しかし、実はこの操作の嬉しいところはこれだけではありません。

$\displaystyle \log{\frac{1}{L_n}}$が１より大きい値になるので、(30)から(31)への式変形 で行ったような「もう一度対数を取る」という操作が 今度こそ 可能になります。

対数ふたたび

ということで、もう一度対数をとると

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{L_{n+1}}}&= {L_n}\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

となりました。

$0 \lt x \lt 1$ において $\displaystyle \log{\frac{1}{x}} \gt 1$ なので、$\displaystyle \log\log{\frac{1}{x}}$ の定義域は $0\lt x \lt 1$ です。
今回は問題なさそうです。

そして $H_n$ についても同じく

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{H_{n+1}}}&= {H_n}\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

が成り立つことがわかります。

従って (8) より

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{L_{\infty}}}=L_{\infty}\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{H_{\infty}}}=H_{\infty}\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

が成り立ちます。

ゆえに $L_{\infty}=H_{\infty}=\mathcal{T}(\mathcal{L})$ であるなら

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{\mathcal{T}(\mathcal{L})}}=\mathcal{T}(\mathcal{L})\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

が成り立つはずです。

ひと工夫

ただ、(35)以降の議論を振り返ると、$x$ が決まったときに $\mathcal{T}(\mathcal{L})$ が一つだけ決まると決めつけて議論を進めるのはちょっと乱暴でした。

そもそも、$x$ の値によっては $\displaystyle \lim_{n\to \infty}T_n$ が振動するという事実がありますから、$\mathcal{T}(\mathcal{L})$ という記号を用いること自体「結論有りき」で進めているような感じがどうしても拭えません。

ということで $\mathcal{T}(\mathcal{L})$ のかわりに $y$ という記号を用いて考察します。

つまり、以下のようにします。

$$\begin{equation} \begin{aligned} \log\log{\frac{1}{y}}=y\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

こうしておけば、あとになって $\mathcal{T}(\mathcal{L})$ に戻すときに「縁のある解だけ拾う」みたいなことができるので、都合がよさそうです。（この時点ではそううまくいくかはわかりませんが...）

なお、$y$ の値域ですが、(46)における $x$ と同じ理由から

$$\begin{equation} 0 \lt y \lt 1 \end{equation}$$

が確定します。

境界値を探す旅

目的のおさらい

ここまでかなり長くなってしまったので、目的をもう一度確認しましょう。
もともとの目的は(6)より

$$\inf \text{dom}(\mathcal{T}) = \mathcal{L}$$

を満たすような $\mathcal{L}$ を求めることでした。

そして、(29)より $L_{\infty}$ と $H_{\infty}$ が一致するような $x$ の境界値こそが $\mathcal{L}$ とわかったので、これを探す、というのが当面の目的になったわけですね。

旅の準備

(51) を $y=f(x)$ のように書けたら話は簡単ですが、どうやらそう簡単には行きません。$x$ と $y$ を分離することすら難しいのではないでしょうか。
なので、式を変形しながら特徴を掴んでいくしかなさそうです。

相変わらずそのままだと扱いづらいので、

$$\begin{equation} \displaystyle u=\log{\frac{1}{y}} \end{equation}$$

と置き換えてみましょう。

このとき、(52) より $u$ の取りうる範囲が

$$\begin{equation} 0 \lt u \end{equation}$$

となることを頭の片隅においておきましょう。

$y=e^{-u}$ に注意すると

$$\begin{equation} \begin{aligned} \log{u}=e^{-u}\log{x} + \log\log{\frac{1}{x}} \end{aligned} \end{equation}$$

となります。

(54)が等式になる条件を見るために $0=$ナントカ の形に整理し、これを関数 $\mathcal{G}(u)$ とします。

$$\begin{equation} \begin{aligned} \mathcal{G}(u)=e^{-u}\log{x} + \log\log{\frac{1}{x}} - \log{u} \end{aligned} \end{equation}$$

両端の観察

$\mathcal{G}(u)$ の極限値や $u=0$ 近辺のようすを調べてみましょう。

具体的には $\displaystyle \lim_{u \to 0}{\mathcal{G}(u)}, \lim_{u \to \infty}{\mathcal{G}(u)}$ をそれぞれ求めておきたいです。

ただ、そうなると $x$ が $\mathcal{G}$ にどのような影響を及ぼすのかを事前に確認する必要があります。

たとえばもし $\log\log{\frac{1}{x}}$ が $+\infty$ やら $-\infty$ を取るようなことがあれば、せっかく $\mathcal{G}$ の頭と後ろの項がうまく計算できても、不定形（$\infty - \infty$ など）になってしまったりして、計算が大変なことになるかもしれません。

対数の性質から $\log{0}=1$ かつ $\displaystyle \lim_{x \to 0}{\log{x}}=-\infty$ ですので

• $\log{x}$ の値域は $0\lt x \lt 1$ において $\mathbb{R}^-$ （負の実数全体）
• $\log{\frac{1}{x}}$ の値域は $0\lt x \lt 1$ において $\mathbb{R}^+$ （正の実数全体）

となることはすぐにわかります。

よって、対数関数の定義が $\log:\mathbb{R}^+ \to \mathbb{R}$ であることを利用すると

$$\log\log: (0,1) \to \mathbb{R}$$

であることが判明します。

よって、区間 $0\lt x \lt 1$ において $x$ が $+\infty$ または $-\infty$ にはならないことがわかります^[3]。

これにより $u$ をパラメータとしたときの $\mathcal{G}$ の極限値においては $\log{x}$ と $\displaystyle \log\log{\frac{1}{x}}$ は定数として考えてよく、(56) から

$$\begin{equation} \begin{aligned} \lim_{u \to 0}{\mathcal{G}(u)}=\infty + \text{Const.} - 0&=\infty\\ \lim_{u \to \infty}{\mathcal{G}(u)}=0+\text{Const.}-\infty&=-\infty \end{aligned} \end{equation}$$

となることがわかりました。

導関数の観察

ここで、$\mathcal{G}$ の微分である $\mathcal{G}'$ は、$\log{x}$ が $u$ にとっては定数であることに注意して

$$\begin{equation} \begin{aligned} \mathcal{G}'(u)&=-e^{-u}\log{x} - \frac{1}{u}\\ &= -\frac{1}{u}\left(e^{-u}u\log{x}+1 \right) \end{aligned} \end{equation}$$

となります。

この関数 $\mathcal{G}'(u)$ はどんな形をしているでしょうか？
それを調べるために、まずはカッコに囲まれた $e^{-u}u\log{x}+1$ について調べてみましょう。

観察 Part.1

まず、$e^{-u}u$ ですが、これを $u$ で微分すると（積の微分法則より）

$$\begin{aligned} \left(e^{-u}u\right)'&=e^{-u} -e^{-u}u\\ &= -e^{-u}(u-1) \end{aligned}$$

となり、もう一度微分すると

$$\begin{aligned} \left(e^{-u}u\right)''=(e^{-u} -e^{-u}u)'&=(e^{-u})' -(e^{-u}u)' \\ &= -e^{-u}-(e^{-u} -e^{-u}u)\\ &= e^{-u}(u - 2) \end{aligned}$$

となります。

これらをもとに

• $-e^{-0}=-1$
• $\displaystyle \lim_{u \to \infty}{-e^{-u}}=0$
• 関数 $y=\pm e^{\pm x}$ は単調関数

などの観察から、(54)の $0 \lt u$ に注意しつつ、以下のような増減表を書くことができます。

$u$	$(0)$	$...$	$1$	$...$	$2$	$...$	$(\infty)$
$\left(e^{-u}u\right)'$	$(1)$	$+$	$0$	$-$	$-e^{-2}$	$-$	$(0)$
$\left(e^{-u}u\right)''$	$(-2)$		$-e^{-1}$		$0$		$(0)$
$e^{-u}u$	$(0)$	$\nearrow$	$e^{-1}$	$\searrow$	$2e^{-2}$	$\searrow$	$(0)$

以上から、$u=1$ のとき $e^{-u}u$ は最大値 $e^{-1}$ をとり、最小値は存在しないことがわかります。
まとめると

$$\begin{equation} \begin{aligned} \begin{cases} 0 \lt {e^{-u}u} \le e^{-1}\\ \underset{u}{\argmax}({e^{-u}u})=1 \end{cases} \end{aligned} \end{equation}$$

が成り立ちます。

観察 Part.2

次に $\log{x}$ ですが、冒頭で $0 \lt x \lt 1$ と決めていたはずですので、真数条件に注意すると

$$\begin{equation} \log{x} \lt 0 \end{equation}$$

とわかります。

ただ、マイナス値だとこの後計算ミスしてしまいそうなので、ある正の実数 ${t}$ を使って

$$\begin{equation} \log{x} = -{t} \end{equation}$$

としておきましょう。

すると $(e^{-u}u\log{x}+1)$ は以下のように書けます。

$$\begin{equation} 1-e^{-u}u{t} \end{equation}$$

関数の形を探る

以上の結果をもとに、改めて $\mathcal{G}(u)$ が $u > 0$ においてどのような関数になるのか、を見ていきます。

注目すべきはもちろん導関数の $\mathcal{G}'$ です。

(61)の ${t} = -\log{x}$ を利用して書きなおすと、以下のようになります。

$$\begin{equation} \begin{aligned} \mathcal{G}'(u)&=-\frac{1}{u}\left(e^{-u}u\log{x}+1 \right)\\ &= -\frac{1}{u}\left(1-e^{-u}u{t} \right) \end{aligned} \end{equation}$$

式の形や(57)から、なんとなく単調減少関数に見えるのですが...
はたして本当にそうでしょうか？

今わかることとして、(54) より $\displaystyle -\frac{1}{u}$ は絶対に $0$ にはなりません。
なので、鍵を握るのは、その右にかけられているカッコの中身です。

そこで、 $\mathcal{D}$ を

$$\begin{equation} \mathcal{D}= 1-e^{-u}u{t} \end{equation}$$

と定義します。

このとき

$$\begin{equation} \begin{aligned} \mathcal{D} \gt 0 &\Leftrightarrow \mathcal{G}'(u) \lt 0\\ \mathcal{D} = 0 &\Leftrightarrow \mathcal{G}'(u) = 0\\ \mathcal{D} \lt 0 &\Leftrightarrow \mathcal{G}'(u) \gt 0 \end{aligned} \end{equation}$$

であることに注意します。

これらを踏まえて、$\mathcal{G}$ の形を考察していきましょう。

ケース1: 単調減少にならない場合

もし、$\mathcal{G}$ が単調減少せず、一度上に浮上することがあるとすれば、それはどんな時でしょうか？

答えは簡単で、$\mathcal{G}$ が極小値と極大値をもてば良いですね。
すなわち $p,q$ を実数として以下の条件を全て満たすときです。

• $p \ne q$
• $\mathcal{G}'(p)=0$ かつ $\mathcal{G}'(q)=0$
• $u=p,q$ の前後で $\mathcal{G}'$ の符号が入れ替わる

$p=q$ のときは、極値をとる$p$の前後で $\mathcal{G}'$ の符号が変化しないので、$\mathcal{G}$ は浮上しない（単調減少する）ことに気をつけましょう。

そこで(57)と(65)に注意しながら増減表を書くと以下のようになります。

$u$	$0$	$...$	$p$	$...$	$q$	$...$	$(\infty)$
$\mathcal{G}'(u)$	$-\infty$	$-$	$0$	$+$	$0$	$-$	$(0)$
$\mathcal{G}(u)$	$\infty$	$\searrow$	$\mathcal{G}(p)$	$\nearrow$	$\mathcal{G}(q)$	$\searrow$	$(-\infty)$

そして、増減表から明らですが、このとき方程式 $\mathcal{D}=0$ は解を2つ持つことがわかります。
言い換えると

$$\begin{equation} (\exist \alpha \in \mathbb{R^{+}}, \exist \beta \in \mathbb{R^{+}},\alpha \lt \beta \Rightarrow \mathcal{G}(\alpha) \gt \mathcal{G}(\beta)) \Rightarrow \#\{x|\mathcal{G}'(x)=0\}=2 \end{equation}$$

ケース2: 単調減少する場合

一方で、$\mathcal{G}$ が単調減少するのはどんな時でしょうか？

答えは、前回とは逆で、$\mathcal{G}'(p)=0$となる$p$ が存在しないか、または $p$ が重解であればよいです。

$u$	$(0)$	$...$	$(\infty)$
$\mathcal{G}'(u)$	$-\infty$	$-$	($0$)
$\mathcal{G}(u)$	$(\infty)$	$\searrow$	$(-\infty)$

この場合、方程式 $\mathcal{D}=0$ は解を1つ持つか、または解をもたないことがわかります。
言い換えると

$$\begin{equation} (\forall \alpha \in \mathbb{R^{+}}, \forall \beta \in \mathbb{R^{+}},\alpha \le \beta \Rightarrow \mathcal{G}(\alpha) \le \mathcal{G}(\beta)) \Rightarrow \#\{x|\mathcal{G}'(x)=0\}\le 1 \end{equation}$$

グラフと境界値

(66)(67)をもとに、改めて $\mathcal{G}(u)$ について考えてみましょう。

$$\mathcal{G}(u)=e^{-u}\log{x} + \log\log{\frac{1}{x}} - \log{u}$$

ここで(61)にならって、 $\log{x}=-{t}$ で書き換えると
(${t}=-\log{x}=\log{x^{-1}}$ および $e^{-{t}}=x$ であることに注意して)

$$\begin{equation} \mathcal{G}(u)=-e^{-u}{t} + \log{{t}} - \log{u} \end{equation}$$

となります。

前項から、このグラフが単調減少するかどうかで、方程式 $\mathcal{G}=0$ の解の数が変わるのした。
ということは、このグラフが単調減少するかどうかで等式(55)が成立する条件も変わってくる、ということですね。

よって、グラフが単調減少するかどうかで場合分けし、それぞれ考察してみます。

Case 1:グラフが単調減少しないとき

$t$ と $u$ が同時に動くと面倒なので、まず、$t$ を固定しておきます。

前節のケース1より、$\mathcal{G}(u)$ が単調減少しない場合は以下のような形になるのでした。

$u$	$0$	$...$	$p$	$...$	$q$	$...$	$(\infty)$
$\mathcal{G}'(u)$	$-\infty$	$-$	$0$	$+$	$0$	$-$	$(0)$
$\mathcal{G}(u)$	$\infty$	$\searrow$	$\mathcal{G}(p)$	$\nearrow$	$\mathcal{G}(q)$	$\searrow$	$(-\infty)$

よって、方程式 $\mathcal{G}(u)=0$ は解を3つ持つことになります。

ところで、(53) より $u=\log{y^{-1}}$ なのですが、$f(x)=\log{x^{-1}}$ は $f:\mathbb{R^{+}}\to \mathbb{R}$ であることに注意すると、$u$ に対応する $y$ が一つずる決まります。

そして $y$ は $L_{\infty}$ と $H_{\infty}$ の候補であったので、おそらくこの3つの解のどれか２つはこの解の候補になると考えることができますが...本当でしょうか？

そこで、グラフが単調減少しないときに $L_{\infty} = H_{\infty}$ となることがあるかどうかを考えてみましょう。

場合分け対策

その前に、グラフが単調減少しないような $t$ ないし $x$ の条件を知っておきたいです。
これを求めておくことで、無駄な場合分けを行わずに済むかもしれません。

$t$ が満たすべき条件は (65) より

$$\mathcal{G}'(u) \gt 0$$

でなければなりません。
従って、(64)(65)から

$$\begin{equation} \begin{aligned} 1-e^{-u}u{t} \lt 0\\ \Leftrightarrow ~ \frac{1}{{t}} \lt e^{-u}u \end{aligned} \end{equation}$$

となるのですが、(59)より $0 \lt {e^{-u}u} \le e^{-1}$ であったので

$$\begin{equation} \frac{1}{t}\lt \frac{1}{e} ~\Leftrightarrow~ e \lt t \end{equation}$$

そして (61) より $t=-\log{x}$ なので

$$\begin{equation} \begin{aligned} &e \lt -\log{x} =\log{x^{-1}}\\ &\Leftrightarrow e^e\lt x^{-1}\\ &\Leftrightarrow x \lt e^{-e} \end{aligned} \end{equation}$$

が導かれます。

模索

話を戻すと、今知りたいのは「区間 $x \lt e^{-e}$ において $L_{\infty} = H_{\infty}$ となることがあるか？」です。

ただ、ちょっと一筋縄では行かなそうです。
何に着目すればいいのか、すぐにはわかりませんね...

もしかしたら、$L_{\infty}, H_{\infty}$ といった書き方がまずいのかもしれません。
もともとこれは $T_n$ によって表現される数列でしたので、$T_n$ に戻してみると、何かひらめくかもしれません。

(7)より

$$\begin{aligned} L_1 = x&, ~~L_{n+1}= x^{x^{L_n}}= T_{2n-1} \\ H_1 = x^x&, ~~H_{n+1}= x^{x^{H_n}}= T_{2n} \end{aligned}$$

だったわけですが、$L_{\infty} = H_{\infty}$ となるのは $T_n$ がただ一つの値に収束する場合に限られるので、区間 $x \lt e^{-e}$ において $T_n$ が収束するかどうか を観察するのがよさそうです。

数列Tの観察

冒頭の 方針の列挙と選定 における 方針候補1 では、ダランベールの収束判定法より $T_n$ の収束を示せないことがわかったのでした。
その最大の理由は「グラフが振動するから」だったのですが、これをちょっとアレンジしてみましょう。

どうするかというと、「グラフ3:n-{Tnの階差数列の絶対値}の関係」と絡めてみます。
つまり、$T_n$ の階差数列を考えてみようという話です。

とはいっても、階差数列をそのまま計算できないことは 方針候補2 ですでに確認しています。
なので、さらにもう一つ工夫が要りそうです。

仮説と模索

せっかく「ダランベールの収束判定法」という道具があるので、これを活用できないか、逆に考えてみましょう。
たとえば、ある実数 $\gamma$ が存在して

$$\begin{equation} \frac{|T_{n+2} - T_{n+1}|}{|T_{n+1}-T_n|}=\gamma \end{equation}$$

という式を評価できるのであれば、ダランベールの収束判定法を適用して収束発散判定ができそうです。
そこで、次のように変形してみます。

$$\begin{equation} |T_{n+2} - T_{n+1}| = \gamma |T_{n+1}-T_n| \end{equation}$$

何やら、数字がたくさん並んでしまいましたが...

そういえば、(12) において四項間漸化式を作ったときも、こんな風に数字がたくさん登場していましたね。
このときに計算した結果を活用できないでしょうか？

すると (10) が

$$\frac{T_{n+2}}{T_{n+1}}=x^{T_{n+1}-T_n}$$

であったので、$x$の右肩に乗っているを(73)に代入できそうです。
よって、(7)より $T_{2n} > T_{2n-1}$ であることに注意しながら (10) を変形すると

$$\begin{equation} \begin{aligned} \log{\frac{T_{n+2}}{T_{n+1}}}&=\log{x^{T_{n+1}-T_n}}\\ &=({T_{n+1}-T_n})\log{x}\\ \therefore T_{n+1}-T_{n}&=\frac{1}{\log{x}}\log{\frac{T_{n+2}}{T_{n+1}}}\\ &=\frac{\log{T_{n+2}-\log{T_{n+1}}}}{\log{x}} \end{aligned} \end{equation}$$

これを(73)に代入して

$$\begin{equation} \begin{aligned} |T_{n+2} - T_{n+1}| = \gamma \left|\frac{\log{T_{n+2}-\log{T_{n+1}}}}{\log{x}}\right|\\ \therefore |T_{n+1} - T_{n}| = \gamma \left|\frac{\log{T_{n+1}-\log{T_{n}}}}{\log{x}}\right| \end{aligned} \end{equation}$$

と、ここまで変形したのはいいですが、絶対値記号がちょっと邪魔です。
この絶対値記号を取っ払えないでしょうか？

ここで再び(7)を思い出してみましょう。
$T_n$ は振動する数列だったので $0 \lt T_n \lt 1$ および、対数関数が単調増加関数であることに注意すると

$$\begin{equation} \begin{aligned} T_{n+1} - T_n \gt 0 \Rightarrow \log{T_{n+1}} - \log{T_n} \gt 0\\ T_{n+1} - T_n \lt 0 \Rightarrow \log{T_{n+1}} - \log{T_n} \lt 0 \end{aligned} \end{equation}$$

であるとわかります。
よって、

$$\begin{equation} T_{n+1} - T_{n} = \frac{\gamma}{\log{x}}(\log{T_{n+1}-\log{T_{n}}}) \end{equation}$$

となり、さらに $T$ を片方に寄せると

$$\begin{equation} \frac{\log{T_{n+1}-\log{T_{n}}}}{T_{n+1}-T_{n}}=\frac{\log{x}}{\gamma} \end{equation}$$

さて...この式の形、どこかで見覚えがないでしょうか?

平均値の定理

(78)は以下のように変形することができますが

$$\begin{equation} \frac{\log{T_{n+1}-\log{T_{n}}}}{T_{n+1}-T_{n}}=\frac{1}{\gamma/\log{x}} \end{equation}$$

もし、この式の右辺を、$n$に依存するようなある実数 $\gamma_n$ を使ってこのように書くとどうなるでしょうか？

$$\begin{equation} \frac{\log{T_{n+1}-\log{T_{n}}}}{T_{n+1}-T_{n}}=\frac{1}{\gamma_n} \end{equation}$$

この式はまさに対数関数についての (ラグランジュの)平均値の定理 を想起させます。
実際、対数関数 $\log{\chi}$ は区間 $T_n \gtrless \chi \gtrless T_{n+1}$ で連続かつ微分可能で、$\displaystyle (\log{\chi})'=\frac{1}{\chi}$ ですから、$T_{n} \gtrless \gamma_n \gtrless T_{n+1}$ を満たすような実数 $\gamma_n$ が存在して、(80)が成り立つことが言えます。

すると (80) について

$$\frac{\log{T_{n+1}-\log{T_{n}}}}{T_{n+1}-T_{n}}=\frac{1}{\gamma_n} \Leftrightarrow \frac{\log{T_{n+2}-\log{T_{n+1}}}}{T_{n+2}-T_{n+1}}=\frac{1}{\gamma_{n+1}}$$

となることに注意して、これに(74)の

$$\begin{aligned} T_{n+1}-T_{n}&=\frac{\log{T_{n+2}-\log{T_{n+1}}}}{\log{x}} \\ \therefore \log{T_{n+2}}-\log{T_{n+1}} &=(T_{n+1}-T_{n})\log{x} \end{aligned}$$

を代入することで

$$\begin{aligned} \frac{(T_{n+1}-T_{n})\log{x}}{T_{n+2}-T_{n+1}}=\frac{1}{\gamma_{n+1}} \end{aligned}$$

となります。
添字が大きものが上に来るようにして、$T$以外を右に寄せると

$$\begin{equation} \frac{T_{n+2}-T_{n+1}}{T_{n+1}-T_{n}}=\gamma_{n+1}\log{x} \end{equation}$$

となります。
ただし、(7)より両辺が負であることを覚えておきます。

なにかしら安全策を取りたいところですが、今度は両辺が負で、かといって絶対値記号を使ったら元の木阿弥なので、いったんこのままで行きます...

右辺の考察

さて、(81)の右辺 $\gamma_{n+1}\log{x}$ はどのような値を取るでしょうか？

これを知るためには、改めて $T_n$ の収束について考えなければなりません...って、そもそもそれを知るために(72)からわざわざここまで来たので、これでは堂々巡りになってしまいます。

今までの議論で、何か再利用できるものはないでしょうか...?

...
そういえば、前回、上限を求める際に、引数 $a$ と $\mathcal{T}(a)$ の極限値 $c$ を用いて、$c=a^c$ という関係式をつくりました。
これは、数列の特性方程式のような役割を期待して作ったものでしたが、この式、もう一度利用できないでしょうか？

と言いたいところですが...そもそもこの式は $T_n$ が収束することを前提としたものです。
$x \lt e^{-e}$ という条件下で収束するかはまだわからないわけです。

とはいえ、このままでは何も進まないので、いったん $T_n$ が収束すると仮定して式の様子を観ながら、矛盾が起きないかを観察することにします。
いわゆる「背理法」を狙ったものです。

その場合、$T_n$ がある実数 $T_{\infty}$ に収束すると仮定すれば、$T_{\infty}=x^{T_{\infty}}$ が成り立つはずです。
よって、ある変数 $w$ を使って $w=x^w$ と書き、これがイコールになるかどうかを調べるための関数

$$\begin{equation} \mathcal{F}(w)=w-x^{w} \end{equation}$$

を観察して、(81)にうまく繋げられないか、を考えることにします。
ただし、$T_{\infty}=x^{T_{\infty}}$ から派生したので

$$\begin{equation} \mathcal{F}(T_{\infty})=0 \end{equation}$$

であることに留意します。
また、$0 \lt x \lt e^{-e}$ という条件により $\mathcal{F}(w)$ は単調増加関数であることに注意します。

仮定と検証

もし $x \lt e^{-e}$ という条件下で $T_n$ が収束するのであれば、(81)が両辺とも負であることに注意して

$$\begin{equation} n \to \infty \Rightarrow -1 \lt \gamma_{\infty}\log{x} \lt 0 \end{equation}$$

となることが、ダランベールの収束判定法により判明します。
ただし $\gamma_{n}$ の収束値を $\gamma_{\infty}$ としました。

これを変形すると

$$\begin{equation} -\frac{1}{\log{x}} \gt \gamma_{\infty} \end{equation}$$

という関係式が成り立ちます。くれぐれも $0 \lt x \lt e^{-e}$ において $\log{x} \lt 0$ であることに注意してください。
ところで、この左辺を $\mathcal{F}$に代入してみると

$$\begin{equation} \begin{aligned} \mathcal{F}\left(-\frac{1}{\log{x}}\right)=-\frac{1}{\log{x}}-x^{-\frac{1}{\log{x}}} \end{aligned} \end{equation}$$

となるのですが、条件 $x \lt e^{-e}$ より $\log{x} \lt -e$ であり、また

$$-\frac{1}{e}=-0.367879441171...$$

なので、 $0 \lt x \lt e^{-e}$ においては

$$\begin{equation} \begin{aligned} \mathcal{F}\left(-\frac{1}{\log{x}}\right)=-\frac{1}{\log{x}}-x^{-\frac{1}{\log{x}}} \lt -\frac{1}{e}-x^{-\frac{1}{e}} \lt 0 \end{aligned} \end{equation}$$

となることが計算によりわかります。

一方で (83) から $\mathcal{F}(T_{\infty})=0$ ですから、$\mathcal{F}$ が単調増加関数であることに注意して

$$\begin{equation} -\frac{1}{\log{x}} \lt T_{\infty} \end{equation}$$

が言えます。

一方、(80)より $T_{n} \gtrless \gamma_n \gtrless T_{n+1}$ であったので、はさみうちの原理から

$$\begin{equation} \begin{cases} \displaystyle \lim_{n\to \infty}{T_{n+1}}=T_{\infty}\\ \displaystyle \lim_{n\to \infty}{T_n}=T_{\infty} \end{cases} \Rightarrow \lim_{n\to\infty}{\gamma_{n}}=T_{\infty}=\gamma_{\infty} \end{equation}$$

となりますので、(88) と (89)から

$$\begin{equation} n \to \infty \Rightarrow -\frac{1}{\log{x}} \lt \gamma_{\infty} \end{equation}$$

となります。

ところが、この(90) は (85) とちょうど不等号が反対であり、矛盾します。

この矛盾は $T_n$ が収束すると仮定したことによるものですから、背理法により $x \lt e^{-e}$ において $T_n$ は収束しないことがわかりました。

以上の結果をまとめると

$$\begin{equation} 0 \lt x \lt e^{-e} \Rightarrow L_{\infty} \ne H_{\infty} \end{equation}$$

となることがわかりました。

Case 2:グラフが単調減少するとき

まず、$t$ を固定しておきます。

もし $\mathcal{G}(u)$ が単調減少するのであれば、$\mathcal{G}(u)$ が定義域内で微分可能であることに注意すると
中間値の定理から $\mathcal{G}(u)=0$ を満たす $u$ が ただ一つだけ 存在します。
この解を $\lambda$ としましょう。すなわち

$$\begin{equation} \mathcal{G}(\lambda) =0 \end{equation}$$

とします。

ところで、(53) より $u=\log{y^{-1}}$ なのですが、$f(x)=\log{x^{-1}}$ は $f:\mathbb{R^{+}}\to \mathbb{R}$ であることに注意すると、$u$ が一つに定まると $y$ も一つに決まります。

そして $y$ は $L_{\infty}$ と $H_{\infty}$ の候補であったので、$y$ が一つに定まるという事実から鳩の巣原理より

$$\begin{equation} L_{\infty}=H_{\infty} \end{equation}$$

が確定します。

この事実と (50)(51)(53) から

$$\begin{equation} \mathcal{T}(\mathcal{L}) = e^{-\lambda} \end{equation}$$

である可能性が出てきます。

これを確かめるため、$t$ （もっというと $x$）が取りうる値について観察してみます。

tの取りうる値

$\mathcal{G}(u)$が単調減少する条件は (67) ですから、前述のケース2の増減表より

$$\mathcal{G}'(u) \le 0$$

でなければなりません。

これと(64)(65)および $\lambda$ を用いると、${t}$ が満たすべき条件は

$$\begin{equation} 1-e^{-\lambda}\lambda{t} \ge 0 \end{equation}$$

であることがわかります。

すると (59) より $\max({e^{-u}u})=e^{-1}$ であることが分かっていますので

$$\begin{equation} 1-e^{-\lambda}\lambda{t} \ge 1-e^{-1}{t} \ge 0 \end{equation}$$

という事実が導かれ、結果

$$\begin{equation} {t}\le e \end{equation}$$

が従います。

よって(61)から

$$\begin{aligned} {t}\le e &\Leftrightarrow -\log{x} \le e\\ &\Leftrightarrow \log{x} \ge -e\\ \end{aligned}$$

$$\begin{equation} \therefore x \ge e^{-e} \end{equation}$$

が成り立ちます。

そしてこれは (29) における $x_0$ を決定できる条件式にほかならず

$$\begin{equation} \mathcal{L} = \inf\text{dom}(\mathcal{T})= e^{-e} \end{equation}$$

が成り立ちます。

以上の結果をまとめると、(93)(98)より

$$\begin{equation} e^{-e} \lt x \lt 1 \Rightarrow L_{\infty} = H_{\infty} \end{equation}$$

であることがわかりました。

これはすなわち

$$\begin{equation} \{x\in \mathbb{R}^+~|~e^{-e}\le x \lt 1 \} \subset \text{dom}(\mathcal{T}) \end{equation}$$

であることを意味します。

本当かな？

念のため、実際に計算してみましょう。
今度は値を計算する代わりに、振動しているかどうかを判定する関数を用意します。

Swift

import Foundation

func judge(x: Double) -> Bool { judge(x: x, loop: 10000000) }
func judge(x: Double, loop: Int) -> Bool {
    var buf = x
    for _ in 0..<loop {
        buf = pow(x, buf)
    }
    let p = buf
    let q = pow(x, buf)
    return abs(p - q) < 1e-9
}

var left = 0.01, right = 1.0
while right - left > 1e-9 {
    let mid = (left + right) / 2
    if judge(x: mid) {
        right = mid
    } else {
        left = mid
    }
}
print(left)

しばらく^[4]待つと、以下のような計算結果が出力されます^[5]。

output

0.06598857145756487

ではWolfram Alpha の計算結果を観てみましょう。
https://www.wolframalpha.com/input?i2d=true&i=Power[e%2C-e]&lang=ja

$$e^{-e}=0.065988035845312537076790187596846424938577048252796436402473541566736330030756308...$$

下6桁まで一致していて、正しい気がします。

ちなみに Wplfram Alpha によれば $e^{-e}$ は 反復指数定数 という名前があるそうです^[6]。

総まとめ

Part 1 では (2)(3)より

$$\begin{aligned} \{x\in \mathbb{R}^+~|~1\le x \le e^{\frac{1}{e}}\} &\subset \text{dom}(\mathcal{T})\\ \sup \text{dom}(\mathcal{T})&=e^{\frac{1}{e}} \end{aligned}$$

を確かめました。

また Part 2 では (99)(101) より

$$\begin{aligned} \{x\in \mathbb{R}^+~|~e^{-e}\le x \lt 1 \} &\subset \text{dom}(\mathcal{T})\\ \inf\text{dom}(\mathcal{T})&= e^{-e} \end{aligned}$$

を確かめることができたので、結果として

$$\text{dom}\left(\mathcal{T}\right) = \{ x\in\mathbb{R}^+~|~ e^{-e}\le x \le e^{\frac{1}{e}} \}$$

を確かめることができました。

脚注

1. グラフ画像を作った後に開始が2だったことに気づいたのですが要点ではないし修正が面倒だったのでこのままにしました🙇。

2. 主観的すぎる文章ですが、「このように考えた」というのを描写するものとご理解いただけると幸いです。

3. 極限値を計算しているわけじゃないので、この文章は正しいと思っているんですが...なんだか怪しい...

4. M1 Max の Mac で約1分ほど待たされます。

5. ループ回数が part 1 のものに比べるとこっそり 10000000 回に増えていますが、単純に 1000000 回だと下4桁までした合致しなかったからです...

6. 一方で $e^{\frac{1}{e}}$ には何も名前がないみたいで、この不公平はなぜ存在するのか気になりますね...