Zenn
Linc'well, inc.Publicationへの投稿
🔢

TypeScriptでクイックソートを実装する

oreo2990
に公開
TypeScript
tech

クイックソートとは？

クイックソートとはソートアルゴリズムの一種で、ランダムに並んでいるデータを昇順または降順に並び替えることができます。
クイックソートでは、以下の操作を繰り返し行い、並び替えを実現します。
① ピボットと呼ばれる基準値を決め、ピボットより大きいグループと小さいグループに分ける
② ① で分けたそれぞれのグループでピボットを決めて、そのピボットより大きいグループと小さいグループに分ける

クイックソートの時間計算量は、ピボットの決め方にもよりますが、ほとんどのケースで O(n log n)となり、バブルソート、選択ソート、挿入ソートなどの O(n^2) の効率の悪いソートアルゴリズムより効率的です。

ちなみに、クイックソートのように元のデータを小さなグループに分割して並び替えていく手法は分割統治法と呼ばれています。これは、大きな問題を小さな問題に分割し、それらを解決することで元の問題を解決するアプローチです。

TypeScript での実装

データを昇順に並び替えるクイックソートを TypeScript で実装すると以下のようになります。

type Swap = {
  array: number[];
  i: number;
  j: number;
};

const swap = ({ array, i, j }: Swap) => {
  const temp = array[i];
  array[i] = array[j];
  array[j] = temp;
};

type Partition = {
  array: number[];
  start: number;
  end: number;
};

const partition = ({ array, start, end }: Partition) => {
  const mid = Math.floor((start + end) / 2);
  const pivot = array[mid];
  swap({ array, i: mid, j: end });

  let i = start - 1;

  for (let j = start; j < end; j++) {
    if (array[j] < pivot) {
      i++;
      swap({ array, i, j });
    }
  }

  i++;
  swap({ array, i, j: end });
  return i;
};

type QuickSort = {
  array: number[];
  start: number;
  end: number;
};

const quicksort = ({ array, start, end }: QuickSort) => {
  if (end - start <= 0) return;

  const pivot = partition({ array, start, end });
  quicksort({ array, start, end: pivot - 1 });
  quicksort({ array, start: pivot + 1, end });
};

const sort = (array: number[]): number[] => {
  const copy = [...array];
  quicksort({
    array: copy,
    start: 0,
    end: copy.length - 1,
  });
  return copy;
};

このコードを実行してみると、以下のような出力になりデータが昇順に並んでいることが確認できます。

const array = [3, 22, 8, 4, 10, 6, 15, 1, 9, 7, 11, 19, 100];
console.log("ソート前の配列:", array);
console.log("ソート後の配列:", sort(array));

/**
 * 実行結果
 * "ソート前の配列:",  [3, 22, 8, 4, 10, 6, 15, 1, 9, 7, 11, 19, 100]
 * "ソート後の配列:",  [1, 3, 4, 6, 7, 8, 9, 10, 11, 15, 19, 22, 100]
 */

コードの解説

各関数について解説します。

swap

type Swap = {
  array: number[];
  i: number;
  j: number;
};

const swap = ({ array, i, j }: Swap) => {
  const temp = array[i];
  array[i] = array[j];
  array[j] = temp;
};

swapは配列の 2 つの要素を交換します。一時変数tempを使って、インデックスiとjの要素を交換します。

partition

const partition = ({ array, start, end }: Partition) => {
  // Part1: ピボットの選択と配置
  const mid = Math.floor((start + end) / 2);
  const pivot = array[mid];
  swap({ array, i: mid, j: end });

  // Part2: 要素の分割
  let i = start - 1;
  for (let j = start; j < end; j++) {
    if (array[j] < pivot) {
      i++;
      swap({ array, i, j });
    }
  }

  // Part3: ピボットの再配置
  i++;
  swap({ array, i, j: end });
  return i;
};

partitionは配列を「ピボットより小さい要素」と「ピボットより大きい要素」の 2 つのグループに分割します。この関数では大きく分けて以下 3 のパートの処理を行います。

Part1 ピボットの選択と配置

// Part1: ピボットの選択と配置
const mid = Math.floor((start + end) / 2);
const pivot = array[mid];
swap({ array, i: mid, j: end });

まず、配列の中央値をピボットとして選択し、そのピボットを swap 関数を使って配列の最後の位置に移動させます。これにより、ピボットを固定した状態で他の要素を整理できるようになります。

例えば、配列 [5, 2, 8, 6, 1, 4, 7] の場合、中央値 array[3] = 6 をピボットとして選択し、ピボット 6 を配列の最後に移動させて、[5, 2, 8, 7, 1, 4, 6] とします。

Part2 要素の分割

// Part2: 要素の分割
let i = start - 1;
for (let j = start; j < end; j++) {
  if (array[j] < pivot) {
    i++;
    swap({ array, i, j });
  }
}

次に、2 つのポインターiとjを使って配列を走査します。iは「ピボットより小さい要素の境界」を示すポインターで、jは「現在チェックしている要素」を示すポインターです。jで指している要素がピボットより小さい場合、その要素をiの次の位置に移動させ（つまり小さいグループに移動させ）、iを 1 つ進めます。

Part1 の例で見ると、i = -1、j = 0 で配列の操作を開始し、以下のような動きになります。

  1. ループ開始前

  2. j = 0 のループ
    array[0] = 5、pivot = 6 であることから、if 文の処理が実行されます。i は -1 から 0 になり、その後 swap 関数で i と j の位置が交換されますが、i、j ともに 0 なので、配列の変化はありません。

  3. j = 1 のループ
    array[1] = 2、pivot = 6 であることから、if 文の処理が実行されます。i は 0 から 1 になり、その後 swap 関数で i と j の位置が交換されますが、i、j ともに 1 なので、配列の変化はありません。

  4. j = 2 のループ
    array[2] = 8、pivot = 6 であることから、if 文の処理がスキップされ、配列の変化はありません。

  5. j = 3 のループ
    array[3] = 7、pivot = 6 であることから、if 文の処理がスキップされ、配列の変化はありません。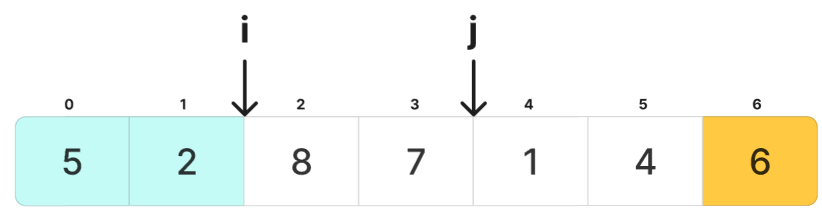

  6. j = 4 のループ
    array[4] = 1、pivot = 6 であることから、if 文の処理が実行されます。i は 1 から 2 になり、その後 swap 関数で i と j の位置つまり 1 と 8 の要素が交換されます。

  7. j = 5 のループ
    array[5] = 4、pivot = 6 であることから、if 文の処理が実行されます。i は 2 から 3 になり、その後 swap 関数で i と j の位置つまり 4 と 7 の要素が交換されます。

Part3 ピボットの再配置

// Part3: ピボットの再配置
i++;
swap({ array, i, j: end });
return i;

最後に、配列の最後に置いたピボットを正しい位置（i+1の位置）に移動させて、ピボットの最終的な位置を返します。この位置より左側にはピボットより小さい要素、右側にはピボットより大きい要素が配置されます。

Part2 の例では、i = 3 だったので、i + 1 = 4 の位置にピボットを移動し、最終結果は [5, 2, 1, 4, 6, 7, 8] となります。最終的に、ピボットの値 6 より小さい要素 [5, 2, 1, 4] が左側、大きい要素 [7, 8] が右側に配置されます。

quicksort

const quicksort = ({ array, start, end }: QuickSort) => {
  if (end - start <= 0) return;

  const pivot = partition({ array, start, end });
  quicksort({ array, start, end: pivot - 1 });
  quicksort({ array, start: pivot + 1, end });
};

quicksortは分割統治法を用いて配列をソートします。この関数では、まず配列の要素が 1 つ以下かどうかをチェックし、そうであれば処理を終了します。

次に、partition関数を呼び出して配列をピボットを境に小さいグループと大きいグループに分割し、そのピボットの位置を取得します。

最後に、ピボットの左側（より小さい要素のグループ）と右側（より大きい要素のグループ）それぞれに対して、再帰的にquicksort関数を呼び出します。これにより、各グループが更に細かく分割され、最終的に全体がソートされた状態になります。

sort

const sort = (array: number[]): number[] => {
  const copy = [...array];
  quicksort({
    array: copy,
    start: 0,
    end: copy.length - 1,
  });
  return copy;
};

sortはソート処理を実行するときに呼び出す関数で、この内部で quick sort を実行します。この関数では、まず元の配列を変更しないよう、配列のコピーを作成します。

次に、作成したコピー配列に対してquicksort関数を呼び出してソートを開始します。この際、配列全体を対象とするため、startに 0、endに配列の最後のインデックスを指定します。

最後に、ソート済みの配列を返します。

以上がコードの解説です。今回の実装では、配列の中央値をピボットとしましたが、ピボットの選び方はクイックソートの効率に大きく影響します。もし常に最小値や最大値をピボットに選んでしまうと、partition による分割が極端に偏ってしまい効率が悪くなります。中央値を選ぶことで、配列がバランス良く分割される可能性が高くなり、多くのケースで O(n log n) の効率的なソートを実現できます。

最後に

今回は代表的なソートアルゴリズムであるクイックソートを TypeScript で実装してみました。partition の部分はコードだけだとわかりづらいので、図にすることで理解しやすくなりました。今回紹介したクイックソート以外にも、マージソート、ヒープソート、シェルソートなど多くのソートアルゴリズムがあるので、それぞれの特徴を調べるのも楽しそうですね。また、分割統治の考え方は生きる上で役に立ちそうです！

参考

https://people.cs.vt.edu/~shaffer/Book/Java3e20100119.pdf

https://book.mynavi.jp/ec/products/detail/id=114278

Linc'well, inc.
Linc'well, inc.Publication

医療スタートアップ Linc'well のエンジニアの記事を集めています。

Discussion