浮動小数点数の情報落ちと最近接丸めと丸め誤差と

突然ですが問題です

下記の処理を行なった後の number の値は？
※ float は32bitの浮動小数点数とします。

float number = 345600.0f;
number += 0.016.0f;

回答

345600.031

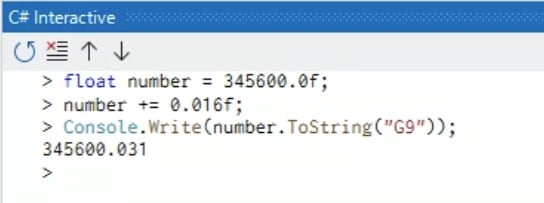
0.016を足したのに、なぜ0.031増えているのかと結構悩んだので、調べてわかったことを書きます。^[1]

解説

分解能をチェック

32bitの浮動小数点数で354600を表現しているとき、1bitの値、つまり分解能は0.031となります。

調べるにはこちらのサイトが便利です。

https://tools.m-bsys.com/calculators/ieee754.php

つまり、0.031より細かい精度を表現することができません。

情報落ち

分解能が0.031の値に0.016を足すとどうなるのか？

情報落ちが発生します。
情報落ちが発生した結果、小さい値は無視され、計算結果は345600のままとなるのではないか？
これが私の予想でした。

丸め誤差

情報落ちが発生した際の挙動はCPUやプログラムからの設定により変わるのですが、デフォルトでは最近接丸め（偶数丸め）となっていることが多いようです。

最近接丸めのロジックを調べたところ、こちらの「浮動小数点における四つの丸めモード」以降の説明がとてもわかりやすかったです。
（書籍の見本ページへのリンクで申し訳ないです）

この丸め処理により切り上げとなり1bit足され、計算結果が345600.031となるというカラクリでした。

誤差って怖い

情報落ちで小さい値を足しても無視される、というのは感覚的にも納得しやすいのですが、「足した値の約倍の値が加算される」というパターンは想定していないと原因究明に時間のかかる不具合に繋がりそうです。

0.016 ≒ 1/60
ということは、60fpsのループでfloatの変数に毎フレーム経過時間（秒）を足し続けて4日経つと、毎フレーム0.031増え続けるようになってしまいます。
こうなると経過時間を保持する変数としてはもう機能しなくなってしまいますね。

「浮動小数点数は精度が重要な値には使用できない」ということはわかっていましたが、今回の調査で「浮動小数点数は使い方を誤ると大きな誤差が生じる可能性がある」と認識を改めました。

脚注

1. 厳密には環境によって異なります。