[拡散モデル] 拡散過程を可視化してみる

はじめに

現在、話題になっている拡散モデルでは、観測データに対して、ノイズを徐々に加えて最終的にノイズのみする拡散過程が使われています。
その拡散過程が実際にどの様にノイズに変換するかを確率分布で可視化してみようと思います。

以下の数式では、拡散モデルの元祖であるDDPM(Diffusion Denoising Probabilistic Models)とそろえます。

https://arxiv.org/abs/2006.11239

以下で使う可視化コードは、こちらにあります。

拡散過程の概要

拡散過程は、観測変数にノイズを徐々に加えていき、最終的にノイズのみの分布( $\bold{x}_T$)にする過程のことである。

ステップを $t$ として、確率変数 $\bold{x}_{t-1}$ から $\bold{x}_t$ への条件付き確率を以下の式で表す。

$$\begin{align} q(\bold{x}_t|\bold{x}_{t-1}) := \mathcal{N}(\bold{x}_t; \sqrt{\alpha_t}\bold{x}_{t-1}, \beta_t) \end{align}$$

データ分布を徐々にノイズ飲みの分布に変化させるために、分散を徐々に大きくする。( $0< \beta_1 < \beta_2 < ... < \beta_T < 1$ )
また、$\alpha_t := 1 - \beta_t$ と定義する。
この様に定義すると、$T$が大きくなるにつれて、$\beta$は、1に近づき、$\alpha$は0に近づくため、$q(\bold{x}_T|\bold{x}_{T-1}) \approx \mathcal{N}(\bold{x}_T; 0, 1)$となる。
また、この式は、$\bold{x}_{T-1}$に関係しないし気になるため、周辺確率が平均0,分散1の平均分布と見なすことができる。

可視化

本章では、ダミーの観測データを作り、(1)式を通じて、どの様に確率分布が推移するかを可視化する。
観測データを混合1次元ガウス分布から何点かサンプリングし、それらを(1)の式で、拡散させ、それぞれのステップごとの確率分布を可視化する。

観測データの確率分布

2つの1次元ガウス分布を混合した混合ガウス分布からサンプリングしたデータを用いる。
この混合ガウス分布の確率変数を$\bold{x_0}$ とする。

• $n=2$
• $\mu_n \in \mathbb{R}$: n番目のガウス分布の平均
• $\sigma_n \in \mathbb{R}^+$: n番目のガウス分布の標準偏差
• $w_n$: n番目分布の混合割合
• $\sum_{i=1}^{n} n_i = 1$

$$f_n(x) = \frac{1}{\sqrt{2 \pi \sigma_n^2}} \exp\left( -\frac{(x - \mu_n)^2}{2 \sigma_n^2} \right) \\ \text{ }\\ f(\bold{x_0} = x) = w_1 f_1(x) + w_2 f_2(x)$$

観測データ生成コード

# 全体のサンプルリング数
n = 200_000

# 2つの1次元ガウス分布の定義
mean1, std1, pi1 = 12, 0.4, 0.3  
mean2, std2, pi2 = 8, 0.7, 1-pi1  
n1 = int(pi1 * n)
n2 = n - n1

# データ生成(観測データ)
data1 = np.random.normal(mean1, std1, n1)
data2 = np.random.normal(mean2, std2, n2)
measured_data = np.concatenate([data1, data2])

# プロット(確率密度を描画する)
plt.figure(figsize=(10, 6))
sns.histplot(measured_data, kde=True, stat='density', linewidth=0, color='blue')
plt.title('生成した観測データ', fontsize=20)
plt.xlim(-5, 20)
plt.grid()
plt.ylabel('Density', fontsize=20)
plt.tight_layout()
plt.savefig('imgs/measured_data.png')
plt.show()

確率分布

拡散過程

拡散のステップ数は、30($T=30$)として、$\alpha_t$, $\beta_t$は、以下の様にスケジューリングする.

# 総ステップ数(拡散を実施する回数)
T = 30

betas = np.linspace(0.01, 0.99, T)
alphas = 1 - betas

plt.figure(figsize=(8, 6))
plt.plot(betas, marker="o", label=r'$ \beta $', markersize=3, alpha=0.8)
plt.plot(np.sqrt(alphas), marker='o', label=r'$ \sqrt{\alpha} $', markersize=3, alpha=0.8)
plt.xlabel('t', fontsize=30)
plt.title(r'$ \alpha, \beta $の可視化', fontsize=20)
plt.legend()
plt.grid()
plt.tight_layout()
plt.savefig('imgs/alpha_and_beta.png')
plt.show()

これらのデータを用いて、拡散過程を実行した結果をバイオリンプロットで可視化する。
この図を見ると、tが増えると、平均が0に近づき、分散も一定になっていくのがみて取れる。
また、観測データ分布の情報はなくなっているのがわかる。

コード

datas = [measured_data]

data_t = measured_data
for t in range(T):
    # 拡散する
    data_t = np.random.normal(loc=np.sqrt(alphas[t]) * data_t, scale=np.sqrt(betas[t]))
    datas.append(data_t)
    
plt.figure(figsize=(12, 8))
sns.violinplot(datas)
plt.axhline(0, color='red', alpha=0.8, linestyle='--')
plt.title('tごとの確率変数($X_t$)の確率分布', fontsize=20)
plt.xlabel('t', fontsize=30)
plt.grid()
plt.ylabel('$x_t$', fontsize=30)
plt.tight_layout()
plt.savefig("imgs/difusion_process.png")
plt.show()

###(Extra)Tensorboardでの可視化
Tensorboardでは、ヒストグラムの軌跡を見ることができる。

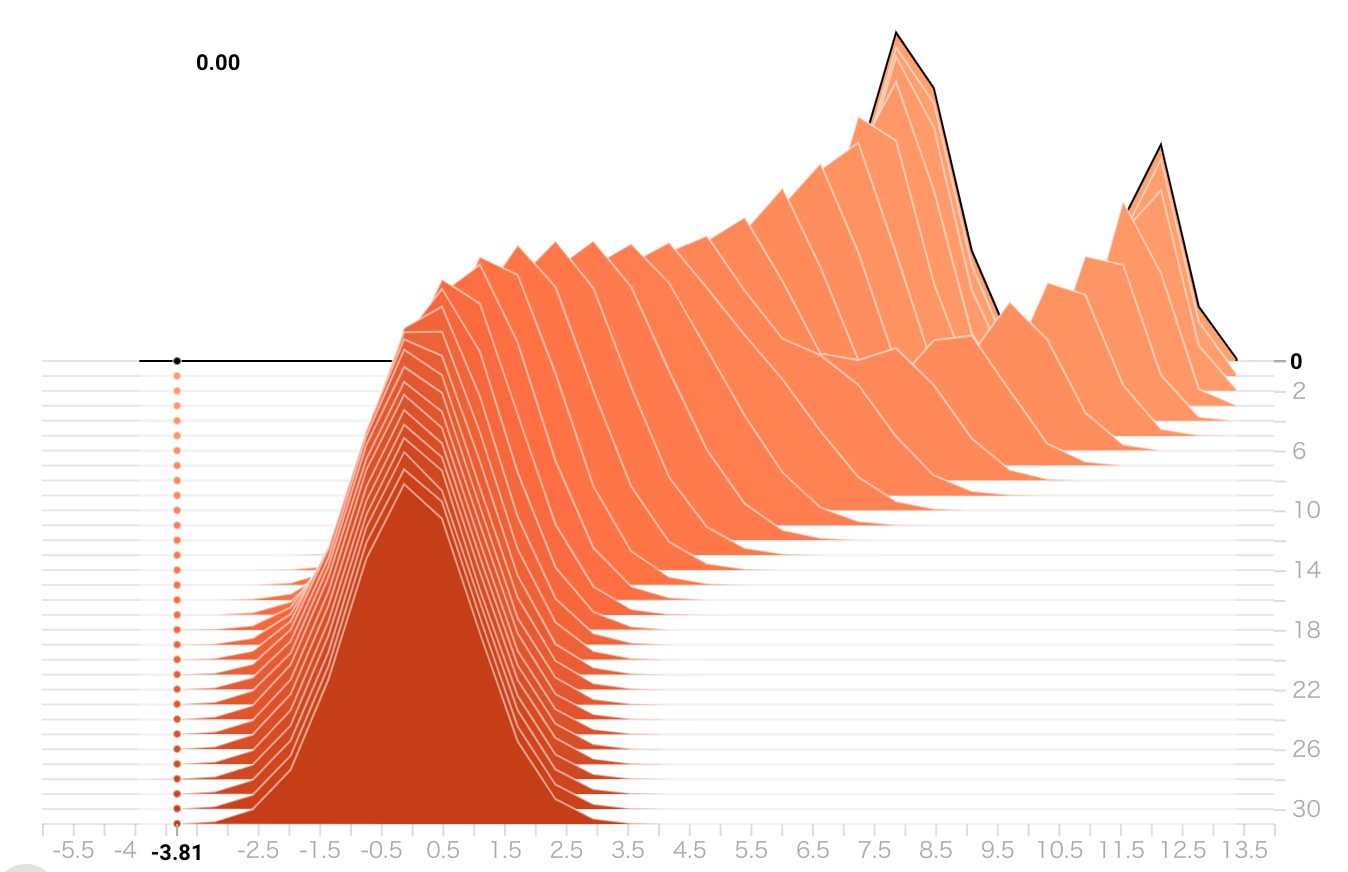
コード

import tensorflow as tf

log_dir = 'logs/diffusion_process/' + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
file_writer = tf.summary.create_file_writer(logdir=log_dir)


tag_name = 'diffusion_process'
with file_writer.as_default():
    # 観測データを記録 (t=0)
    tf.summary.histogram(tag_name, measured_data, step=0)
    
    for t, data_t in enumerate(datas, start=1):
        tf.summary.histogram(tag_name, data_t, step=t)

# tensorboardを起動して、拡散過程を見る。
# ブラウザからlocalhost:6006にアクセス
!tensorboard --logdir=logs/diffusion_process --port=6006