有限要素法による非時間依存1次元シュレディンガー方程式
n番煎じですがやってみたかったので.
理論編
理論と題するのもおこがましいほどですが少しだけ説明を.
1.有限要素法とは?
対象とする領域を小領域(要素)に分割し, 各領域ごとに適当な近似関数で解を近似する方法. 具体的には, 微分方程式を用いて各要素ごとに近似関数が満たすべき連立方程式を作成し, 各要素同士の関係から全体の連立方程式を作成, これを解きます. 今回はシュレディンガー方程式が対象なので, 解くべき方程式は一般化固有方程式となります.
今回行う方法は, 有限要素法の中でもGalerkin法と呼ばれるものです. これは重み付き残差法の一種で, 特に近似関数の基底と重み関数の基底が同じ関数系であるものを言います.
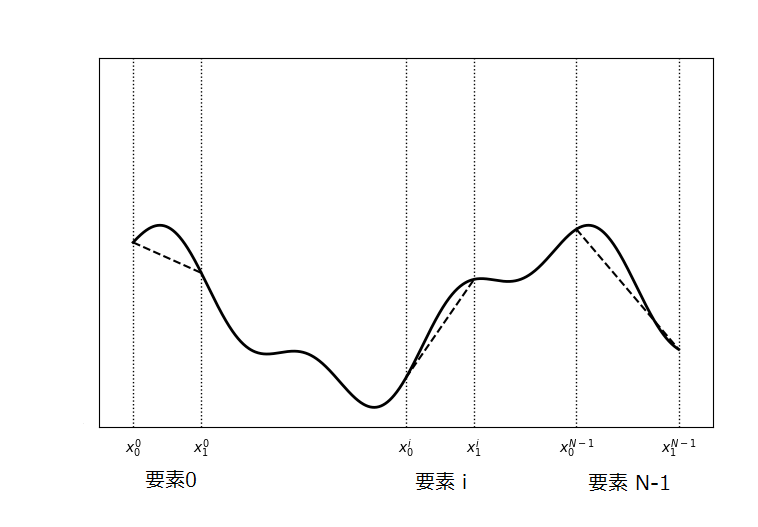
近似のイメージ
2.シュレディンガー方程式
時間に依存しない1次元のシュレディンガー方程式は以下の式(2.1)で与えられます.
この記事では式(2.1)ではなく, 以下の式(2.2)に示す時間に依存しないシュレディンガー方程式を解きます.
計算編
3.弱形式を求める
重み関数として
式(3.1)左辺第1項の積分に対して部分積分を施すと以下の式(3.2)を得ます.
ただし, 1行目から2行目への変形にはDirichlet境界条件
4.形状関数
対象区間
と表現できます. ただし,
とします. つまり,
5.離散化
式(4.1)を用いると,
同様に, ポテンシャル
と書けます. これらを式(3.3)の弱形式に代入すると
を得ます. さらに,
を得ます.
6.要素行列を求める.
式(5.1)をさらに計算していきましょう. 式(5.1)左辺第1項は
式(5.1)左辺第2項は
式(5.1)右辺は
以上をまとめると以下を得ます.
7.全体行列を構成する
式(6.1)は
と書き表せます. さらに, 変分原理を用いることで以下のような方程式に変形できます(らしいです. 変分原理について勉強したらしっかり書きます).
行列
さらに, Dirichlet境界条件
後はこれを解くだけですが, 今回はライブラリに任せます. そのうち別記事にまとめるかもしれません.
プログラミング編
8.Pythonで有限要素法
おまけ
import numpy as np
import matplotlib.pyplot as plt
from collections.abc import Callable
import scipy.sparse.linalg as spsl
class SchrodingerFEM():
DIRAC_CONSTANT: float = 1.054571817e-34
DIRAC_CONSTANT_DOUBLE: float = DIRAC_CONSTANT**2
EIG_VAL_FILE = 'eigenvalue.csv'
EIG_VEC_FILE = 'eigenvector.csv'
n: int
m: float
matrix_genned: bool
x: np.ndarray
l: np.ndarray
A: np.ndarray
B: np.ndarray
eigen_val_vec: list
V: Callable[[float], float]
def __init__(self, n: int, m: float, x: np.ndarray, V: Callable[[float], float])->None:
self.n = n
self.m = m
self.x = x
self.V = V
self.matrix_genned = False
self.eigen_val_vec = []
if len(x) != n+1:
raise ValueError(f'Array x size should be {n+1} but is {len(x)}.')
self.l = np.zeros((n,))
for i in range(n):
self.l[i] = self.x[i+1]-self.x[i]
self.A = np.zeros((n+1, n+1), np.float64)
self.B = np.zeros((n+1, n+1), np.float64)
def gen_A_element(self, e)->np.ndarray:
Ae = np.zeros((2, 2), np.float64)
Ae[0][0] = self.DIRAC_CONSTANT_DOUBLE/(2*self.m*self.l[e])+self.l[e]*(3*self.V(self.x[e])+self.V(self.x[e+1]))/12
Ae[0][1] = -self.DIRAC_CONSTANT_DOUBLE/(2*self.m*self.l[e])+self.l[e]*(self.V(self.x[e])+self.V(self.x[e+1]))/12
Ae[1][0] = Ae[0][1]
Ae[1][1] = self.DIRAC_CONSTANT_DOUBLE/(2*self.m*self.l[e])+self.l[e]*(self.V(self.x[e])+3*self.V(self.x[e+1]))/12
return Ae
def gen_B_element(self, e)->np.ndarray:
Be = np.zeros((2, 2), np.float64)
Be[0][0] = self.l[e]/3
Be[0][1] = self.l[e]/6
Be[1][0] = Be[0][1]
Be[1][1] = Be[0][0]
return Be
def gen_matrix(self)->None:
for e in range(self.n):
Ae = self.gen_A_element(e)
Be = self.gen_B_element(e)
for i in range(2):
for j in range(2):
self.A[e+i][e+j] += Ae[i][j]
self.B[e+i][e+j] += Be[i][j]
self.A, self.B = self.A[1:self.n, 1:self.n], self.B[1:self.n, 1:self.n]
print('Matrix calculation has done !\n\n', end='')
self.matrix_genned = True
def solve(self)->None:
if not self.matrix_genned:
raise ValueError('Matrix has not been generated.')
val, vec = spsl.eigs(self.A, self.n, self.B, maxiter=self.n*500, which='SM', sigma=0.05)
for i in range(len(val)):
self.eigen_val_vec.append((val[i], np.concatenate([[0], vec[:, i], [0]])))
self.eigen_val_vec.sort(key=lambda x:x[0])
def get_matrix(self)->tuple[np.ndarray, np.ndarray]:
return self.A, self.B
def get_eigenvalue(self, i)->np.complex64:
return self.eigen_val_vec[i][0]
def get_eigenvector(self, i)->np.ndarray:
return self.eigen_val_vec[i][1]
def export_data(self)->None:
val_file_handler = open(self.EIG_VAL_FILE, mode='w')
vec_file_handler = open(self.EIG_VEC_FILE, mode='w')
for val_vec in self.eigen_val_vec:
val_file_handler.write(f'{val_vec[0]}\n')
vec_file_handler.write(','.join(map(str, val_vec[1]))+'\n')
val_file_handler.close()
vec_file_handler.close()
def V(_ :float)->float:
return 0
def V0(x: float)->float:
return x**2
def V1(x: float)->float:
if abs(x)>2:
return 10
else:
return 0
if __name__=='__main__':
N = 500
m = SchrodingerFEM.DIRAC_CONSTANT_DOUBLE/2
L = 5
x = np.linspace(-L, L, N+1)
fem = SchrodingerFEM(N, m, x, V0)
fem.gen_matrix()
fem.solve()
fem.export_data()
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$\phi$')
for i in range(3):
ax.plot(x, fem.get_eigenvector(i), label=f'$E_{i+1}: {fem.get_eigenvalue(i)}$')
ax.legend()
plt.show()
7.例
実際にいくつかのポテンシャルで計算してみました.
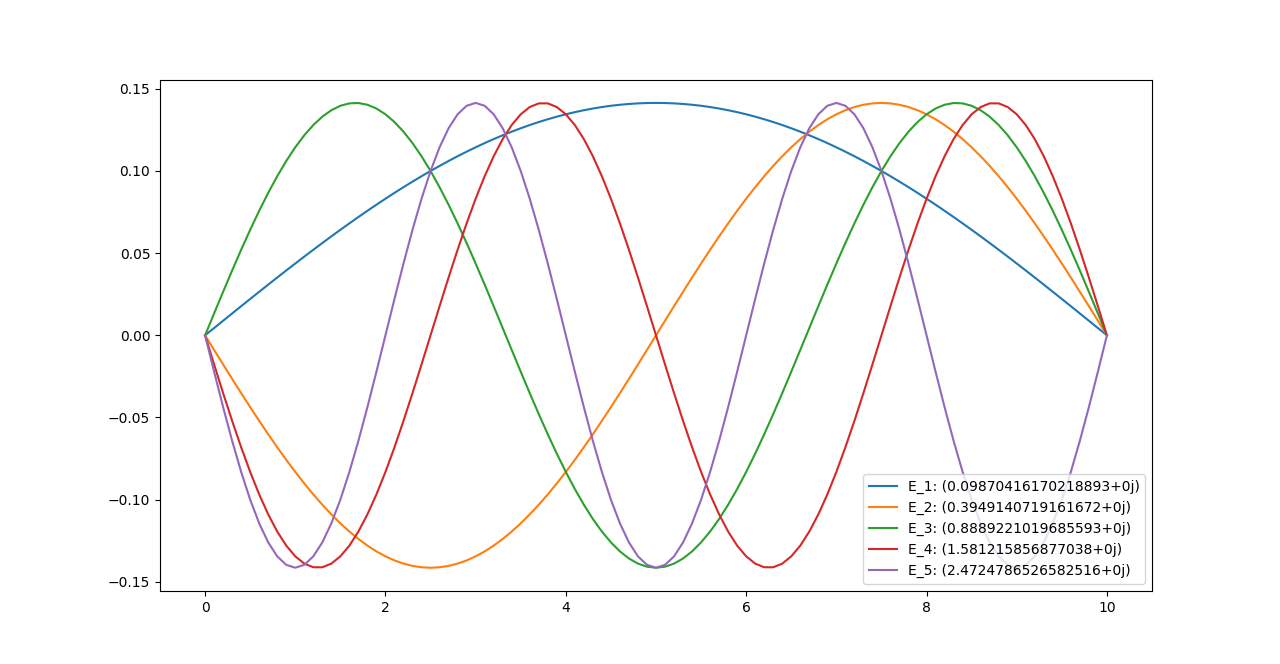
無限に深い井戸型ポテンシャル

調和振動子ポテンシャル
固有値の番号は小さい方から1, 2, ... と振っているので注意.
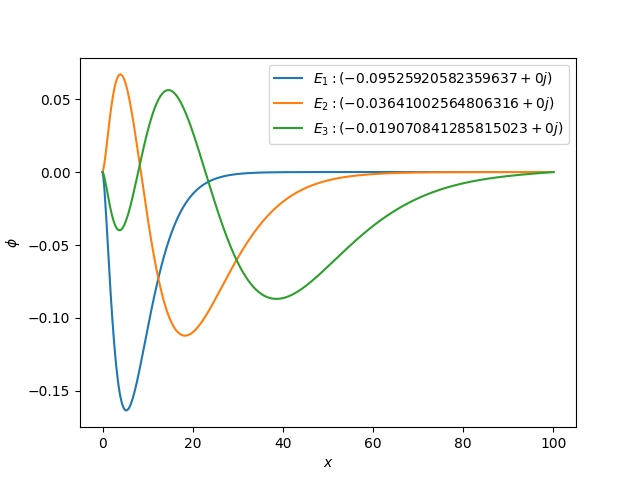
クーロンポテンシャル
参考
@cometscome_phys Yuki Nagai. "1次元シュレーディンガー方程式を有限要素法で解いてみる in Julia". https://qiita.com/cometscome_phys/items/fbeaa92fcb4b6d8c6240
@dc1394. "水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる(C++とJuliaのソースコード付き)". https://qiita.com/dc1394/items/c0d3d02fa738b040128c
@Sunset_Yuhi. "Pythonで1次元有限要素法(Poisson方程式)". Pythonで1次元有限要素法(Poisson方程式)". https://qiita.com/Sunset_Yuhi/items/4c4ddc25609a7619cce0
Discussion