「なぜ人は利益は確定しようとするのに損失は運任せでも回避しようとするのか」をシミュレーションで解明できた？
はじめに
行動経済学の知見の一つに「損失回避の法則（プロスペクト理論）」というのがあります。例えば以下のような選択肢があったとします。
1: 選択肢A:100万円が無条件で手に入る。
2: 選択肢B:コインを投げ、表が出たら200万円が手に入るが、裏が出たら何も手に入らない。
この二つは手に入る金額の期待値は同じ100万円ですが、ほとんどの人は（おそらくあなたも）100万円が無条件で手に入る方を選びます。
一方で以下のような質問をされたとします。
1: 選択肢A:無条件で借金が100万円減額され、借金総額が100万円となる。
2: 選択肢B:コインを投げ、表が出たら借金が全額免除されるが、裏が出たら借金総額は変わらない。
この場合も期待値が-100万円で 同じ であることは変わりません。しかしほとんどの人は前回と打って変わって2番目のギャンブル性のある選択肢を選びます。
このように人は利益は確定させようとするのに損失は運任せにしてでも回避しようとするというパラドックスがあります。これが 損失回避の法則 です。
Wikipediaではこの理由について「価値の大きさは金額と比例関係にない」というモデルで説明しています。金額が2倍になっても価値は1.6倍程度にしかならないため確実な100万円の方が50％の確率の200万円より大きくなるというわけです。
ただ自分は「実は損失を運任せでも回避しようとするのは合理的な選択なのではないか」と考えその仮説をコンピュータ・シミュレーションで検討してみることにしました。
シミュレーションの方法
- まず、人間と同じように「損失回避の法則」に従って選択肢を選ぶエージェント、反対の法則に従って選択肢を選ぶエージェント、そして対照群として常に確定ポイントの選択肢を選ぶエージェント、常に運任せの選択肢を選ぶエージェントを2^24(1677万7216)体ずつ作ります（最初100体でシミュレーションを行ってましたがそれだと少なすぎるせいか結果が毎回異なってしまいました）。
- 各エージェントは最初「100ポイント」を持ってます。
- 各エージェントに対してランダムに生成された質問し、回答から「ポイント」の増減を行います。これを1000回繰り返します。
- 「ポイント」がゼロ以下になったエージェントは「死亡」し、以降ポイントを得ることはできません。
- 各種エージェントの「生存者」数と「ポイント」の合計の推移を記録します。
2-1の「死亡」は現実世界に当てはめると「一度餓死するとその後いくら食料を与えても生き返らない」「一度資金がゼロになるとそれ以降市場に参加できない」といったことを意味します。これが自分が「実は損失を運任せでも回避しようとするのは合理的な選択なのではないか」と考えた理由です。一度「死亡」してしまえばもうチャンスはなくなってしまうのだから運任せでも損失を回避しようとするのが合理的ではないかと考えました。
シミュレーションの実装
まず質問を以下のようにクラスで表現します。最初に得するか損するかの種類。
public enum Kind {
PROFIT, LOSS
}
次に何％の確率で何ポイント増減するかを表すrecord。
public record Candidate(double probability, int point) {}
そして二つを合わせ確定でポイントがもらえる/失うときのポイント数を追加した「質問」record
public record Question(Kind kind, int fixedPoint/* 確定ポイント */, ArrayList<Candidate> candidateList) {}
そして「質問者」を作成しランダムで「質問」を生成します。
public class Questioner {
private static final Random RANDOM = new Random();
public static Question question() {
int absOfExpectedValue = (int) (10 + 10 * (RANDOM.nextDouble() - 0.5));
//Profitable options with a 50% chance
if (RANDOM.nextDouble() < 0.50) {
final ArrayList<Candidate> PROFIT_CANDIDATE_LIST = new ArrayList<>() {
{
add(new Candidate(0.50, absOfExpectedValue * 2));
add(new Candidate(0.50, 0));
}
};
return new Question(Kind.PROFIT, absOfExpectedValue, PROFIT_CANDIDATE_LIST);
} else {
final ArrayList<Candidate> LOSS_CANDIDATE_LIST = new ArrayList<>() {
{
add(new Candidate(0.50, -absOfExpectedValue * 2));
add(new Candidate(0.50, 0));
}
};
return new Question(Kind.LOSS, -absOfExpectedValue, LOSS_CANDIDATE_LIST);
}
}
}
次に以下のようなAgentインターフェースを作成します。
public interface Agent {
int FIRST_POINT = 100;
Random RANDOM = new Random();
void choose(Question question);
int point();
//「死亡」する
void die();
//「死亡」しているかどうか
boolean dead();
}
そして以下のように「質問」に対する「回答」を行いポイントを増減する処理を実装します。
/**
* This agent chooses an option like a human,
* if there is a possibility of profit, choose a fixed points option,
* and if there is a possibility of loss, choose a probabilistic points option.
*/
public class Human implements Agent {
@Override
public void choose(Question question) {
//利益が得られる質問なら確定ポイントを選ぶ
if (question.kind() == Kind.PROFIT) {
point = point + question.fixedPoint();
return;
}
//損する可能性がある質問なら運任せの選択肢を選ぶ
else {
var r = RANDOM.nextDouble();
var probabilitySum = 0.0;
for (Candidate candidate : question.candidateList()) {
probabilitySum += candidate.probability();
if (r < probabilitySum) {
point = point + candidate.point();
return;
}
}
}
}
/** 以下略 */
}
同じ要領で人間と反対の傾向で選択肢を選ぶエージェントなどを作っていきます。
後は以下のように質問、回答を1000回実行する処理を行うだけです（長いですがやってることは単純なので読み飛ばして構いません）。
//Generate players
final int FIRST_PLAYER_NUM = (int) Math.pow(2, 24);//16,777,216
int humanNum = FIRST_PLAYER_NUM;
int contrarianNum = FIRST_PLAYER_NUM;
int cowardNum = FIRST_PLAYER_NUM;
int gamblerNum = FIRST_PLAYER_NUM;
var humanList = new ArrayList<Human>() {{
for (int i = 0; i < FIRST_PLAYER_NUM; i++) {
add(new Human());
}
}};
var contrarianList = new ArrayList<Contrarian>() {{
for (int i = 0; i < FIRST_PLAYER_NUM; i++) {
add(new Contrarian());
}
}};
var cowardList = new ArrayList<Coward>() {{
for (int i = 0; i < FIRST_PLAYER_NUM; i++) {
add(new Coward());
}
}};
var gamblerList = new ArrayList<Gambler>() {{
for (int i = 0; i < FIRST_PLAYER_NUM; i++) {
add(new Gambler());
}
}};
//Simulation
File survivorNumFile = new File("survivor_num.tsv");
File pointSumFile = new File("points_sum.tsv");
try (FileWriter survivorNumFileWriter = new FileWriter(survivorNumFile);
FileWriter pointSumFileWriter = new FileWriter(pointSumFile)) {
survivorNumFileWriter.write("Count\tHuman\tContrarian\tCoward\tGambler\n");
pointSumFileWriter.write("Count\tHuman\tContrarian\tCoward\tGambler\n");
for (int i = 0; i < 1000; i++) {
long humanPointSum = 0;
long contrarianPointSum = 0;
long cowardPointSum = 0;
long gamblerPointSum = 0;
for (int j = 0; j < FIRST_PLAYER_NUM; j++) {
if (humanNum > 0) {
var human = humanList.get(j);
if (!human.dead()) {
var question = Questioner.question();
human.choose(question);
if (human.point() <= 0) {
human.die();
humanNum--;
} else humanPointSum += human.point();
}
}
if (contrarianNum > 0) {
var contrarian = contrarianList.get(j);
if (!contrarian.dead()) {
var question = Questioner.question();
contrarian.choose(question);
if (contrarian.point() <= 0) {
contrarian.die();
contrarianNum--;
} else contrarianPointSum += contrarian.point();
}
}
if (cowardNum > 0) {
var coward = cowardList.get(j);
if (!coward.dead()) {
var question = Questioner.question();
coward.choose(question);
if (coward.point() <= 0) {
coward.die();
cowardNum--;
} else cowardPointSum += coward.point();
}
}
if (gamblerNum > 0) {
var gambler = gamblerList.get(j);
if (!gambler.dead()) {
var question = Questioner.question();
gambler.choose(question);
if (gambler.point() <= 0) {
gambler.die();
gamblerNum--;
} else gamblerPointSum += gambler.point();
}
}
if (humanNum == 0 && contrarianNum == 0 && cowardNum == 0 && gamblerNum == 0)
break;
}
survivorNumFileWriter.write((i + 1) + "\t" + humanNum + "\t" + contrarianNum + "\t" + cowardNum + "\t" + gamblerNum + "\n");
pointSumFileWriter.write((i + 1) + "\t" + humanPointSum + "\t" + contrarianPointSum + "\t" + cowardPointSum + "\t" + gamblerPointSum + "\n");
if (humanNum == 0 && contrarianNum == 0 && cowardNum == 0 && gamblerNum == 0)
break;
}
} catch (IOException e) {
System.out.println(e);
}
結果
生存者数、ポイントの合計の推移のグラフは下記のようになりました。
- Human(人間):「損失回避の法則」に従って選択肢を選ぶ
- Contrarian(逆張り):人間と反対の法則で選択肢を選ぶ
- Coward(臆病):常に確定ポイントの選択肢を選ぶ
- Gambler(ギャンブラー):常に運任せの選択肢を選ぶ
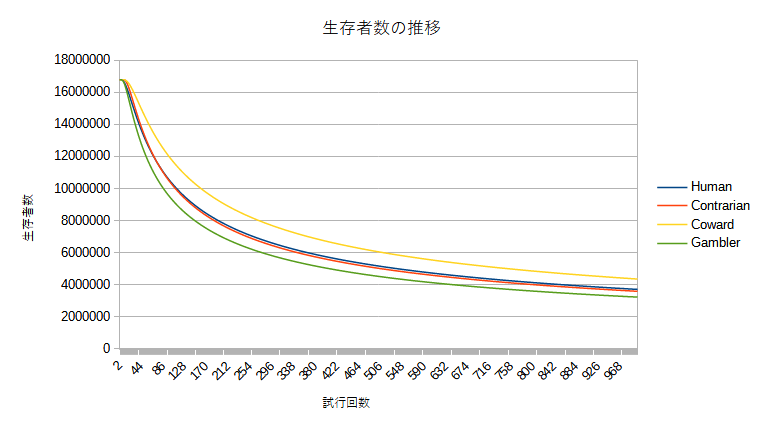
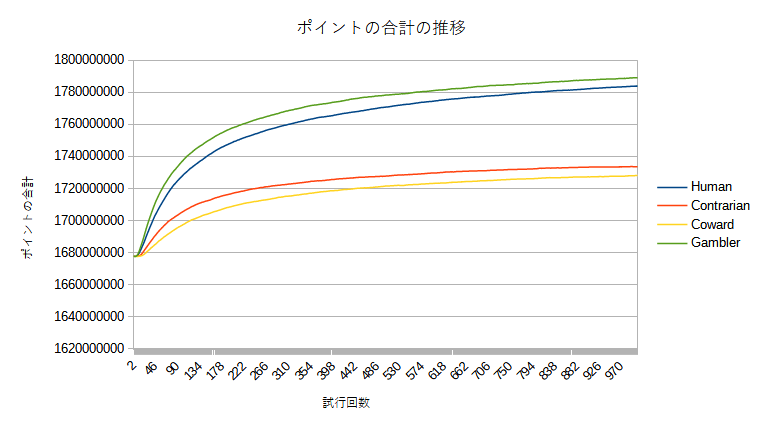
Humanは（少しの差ですが）生存率ではCoward戦略に負けポイントの合計ではGamblerに負けるという結果が出ました。ただ「生存率」と「ポイントの合計」両方を考慮するとどちらでも2位で良い成績を出しているHuman（損失回避の法則）が総合的に見ると最も良い戦略である、と解釈することも可能かもしれません。実際、「生存率」ではトップのCowardは「ポイントの合計」ではGambler、Humanに大きく水をあけられ最下位です。また、Gamblerは「ポイントの合計」では僅差でトップを取りましたが「生存率」では最下位です。
ただし @akinomyoga さんが指摘してるようにあくまで「このシミュレーションルールの下では」という但し書きがつきます。
使用したコードはすべてGithubにアップしたので興味がある方はご覧ください。実はコードに誤りがあったとかだったら恥ずかしいので検証してくれる方はお願いします。また、今回のシミュレーションのために最新版までのJavaの文法を調べましたが、元はJava 8で知識が止まっていたので現在はもっと楽な書き方があるよという点があったらご教授お願いします。あるいはKotlinの方がいいとかも。
Discussion