Zenn
Open39

E資格勉強scrap

ディープラーニング
E資格
kyo-dskyo-ds

シソーラスとは

  • 単語の意味が似ているものをコンピューターにわかる形式でまとめたもの
    • car: SUV, automobile, motorcar,, など
  • 種類
    • 単純に似た単語をまとめたもの
    • 構造上に整理したもの
  • 有名なシソーラス
    • word net
      • 単語ネットワークも利用可能なもの
  • シソーラスの課題
    • 時代の変化への対応が困難
      • スラングなどで常に意味が変わるものがある
    • 作業コストが高い
      • 人がそれらを構築するのには大量な人的コスト
    • 単語の細かなニュアンスが表現できない
kyo-dskyo-ds

コーパス

特定の目的のために収集されたテキストデータの集合を指す。
データサイエンスや機械学習の分野では、特に自然言語処理（NLP）のタスクにおいて頻繁に使用される概念である

python:テキストをwordsにしてコーパスに変換する前処理が以下

def preprocess(text):
  text = text.lower()
  #ピリオドの前にスペースをいれて一つのトークンとして扱う
  text = text.replace('.', ' .')
  words = text.split()

  word_to_id ={}
  id_to_word = {}
  for word in words:
    if word not in word_to_id:
      new_id = len(word_to_id)
      id_to_word[new_id] = word
      word_to_id[word] = new_id

  corpus = np.array([word_to_id[w] for w in words])

  return corpus, word_to_id, id_to_word
kyo-dskyo-ds

分布仮説

  • 単語をベクトル要素として表現したいモチベーションがある

    • 画像を例にとると色の名前で表現するよりも、RGB=(x, y, z)のような形で表現するほうが
      簡潔でわかりやすい
    • 単語も同じように意味をベクトル表現したい

  • 分布仮説とは？

    • 単語の意味は、周囲の単語の分布によって形成されるというもの
    • どゆこと？
      • 単語自体には意味がなく、」その単語のコンテキスト（文脈）に意味があるという考え

    ウィンドウサイズとは

    • コンテキストのサイズのこと
    • 周りのどのくらいの単語をコンテキストとして認識するかを定義する

https://www.acceluniverse.com/blog/developers/2019/11/-deep-learning2-1-2-3.html

kyo-dskyo-ds

共起行列

  • 分布仮説に基づいて、単語をベクトル表現するための行列のことを指す。
  • 考え方はシンプルで、ある単語に注目するとき（ある単語をベクトル化するとき）
    その単語の周囲の単語（コンテキスト）をカウントする。
  • これは、カウントベースの手法、統計的手法などと呼ばれる。

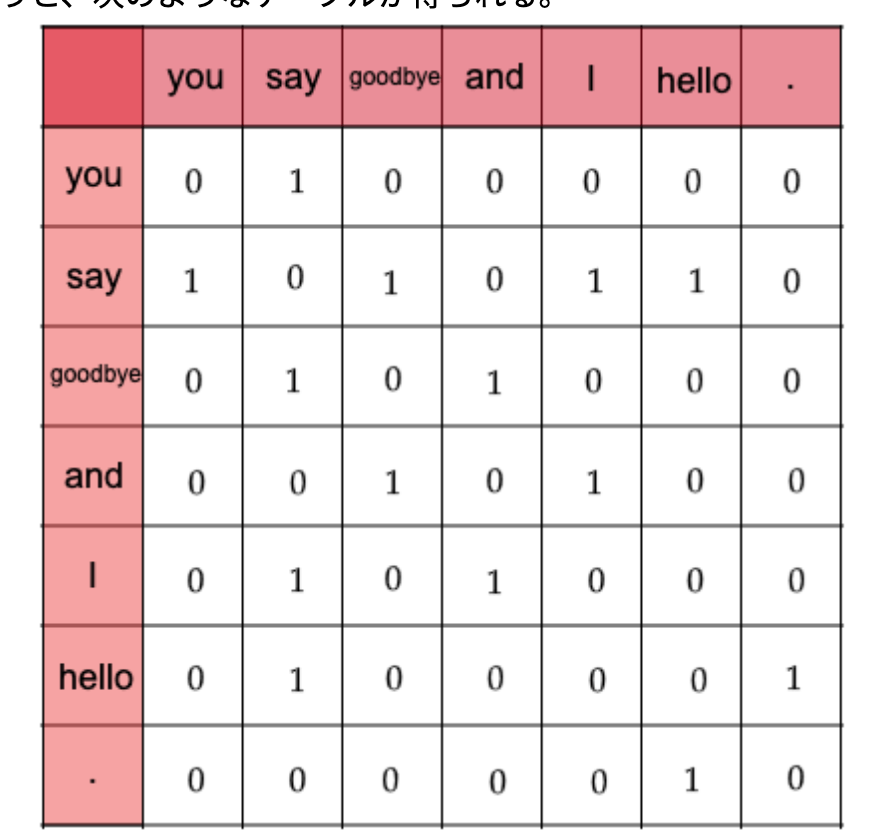
実装はskip

kyo-dskyo-ds

ベクトル間の類似度

  • ベクトルの類似度計算には、内積やユークリッド距離などが代表例としてある
  • 単語ベクトルの類似度計算にはcos類似度がよく用いられる

    ポイントはベクトルを正規化してから内積を取っている点

    数式

{Cosine Similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} ​

分子にベクトルの内積、分母に各ベクトルのノルムを計算している
ノルムはベクトルの大きさを表していてここではL2ノルムを計算している

def cos_similarity(x, y):
    nx = x / np.sqrt(np.sum(x**2))
    ny = y / np.sqrt(np.sum(y**2))
    return np.dot(nx, ny)

厳密にはゼロ除算対策でイプシロンを足してあげる必要がある

kyo-dskyo-ds

カウントベース手法の改善

  • カウントベース手法の問題点とは？
    • 共起行列はコンテキスト内の2つの単語が共起した回数を形状している
    • The という単語を考えたとき、theというのはそもそもの出現回数が多いため
      例えば、car という単語の関係を考えたときに、drive の単語は非常に関係性が強い単語だが
      単純に回数カウントで考えると the car などの生起回数は非常に高く
      carに対して driveよりもtheの方が関係性が強いと表現される
      →望まない状況
  • どうしたらいいの？
    • それぞれの単語の単独での生起確率を考慮してあげればよいのでは？

相互情報量

相互情報量(PMI)とは、xとyという確率変数に対して、下記で定義される

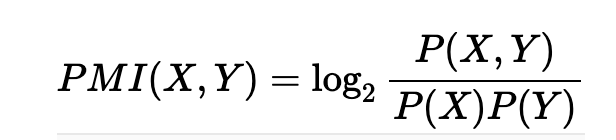
このまま使うと、同時確率P(x, y)がゼロのときに、-∞になってしまうので
実用上は下記のように、PMIが0以下の場合は0として扱う。これをPPMIと呼ぶ

相互情報量、カウントベース手法の問題点

ここまで改善しましたが、まだ問題点がある。
それは共起行列、PPMI行列の場合も、コーパスをもとに
単語のユニーク数*単語のユニーク数の行列ができるが、コーパスの語彙数分の次元数が当然必要になる。
これは非常に疎な行列でほとんどが0の行列になり、ノイズに弱く頑健性に乏しい。

kyo-dskyo-ds

word2vec

単語をベクトル化するために、カウントベース、PPMI、その次元削除などがあったが
結局膨大なコーパスに対して、行列を求めてそれをSVDで次元削除することは非現実的。
→推論ベースの手法が発案

推論ベースの手法の何が嬉しいか

  • コーパスすべてを一気に扱う必要がない
    • カウントベースの手法は一気にコーパスを学習する必要がある
      • コーパス全体から行列算出→一気にSVD処理
    • 推論ベースでは、ミニバッチの形でニューラルネットワークで逐次的に学習できる

推論ベース手法の概要

  • 推論ベースの手法では周辺の単語（コンテキスト）から該当の単語を推測するよう学習し
    その結果として単語ベクトルを得る。

    word2vevには2つの手法がある

    • Word2vecでは下記2つのモデルが使用される
      • CBOW(continuous bag-of-words)
        -前後いくつかの単語の間の単語を予測する
      • skip-gram
        • 1単語の前後の単語を予測する

CBOW（Continuous Bag of Words）

CBOWは、周辺の単語（文脈）から中心の単語を予測するモデル

特徴
入力：周辺の単語
出力：中心の単語
効率：計算効率が高い
学習速度：高速

  • 具体例

    • 例えば、次のような文章があるとします。
      The quick brown fox jumps over the lazy dog

    • ここで、「fox」が中心の単語だとすると、CBOWは周辺の単語である「The quick brown」と「jumps over the lazy dog」を使って「fox」を予測します。

    • 周辺の単語 → 中心の単語

      • (the, quick, brown, jumps, over, the, lazy, dog) → fox

Skip-gram

Skip-gramは、中心の単語から周辺の単語（文脈）を予測するモデルです。

特徴
入力：中心の単語
出力：周辺の単語
効率：計算効率がやや低い
学習速度：遅いが、精度が高い

  • 具体例
    • The quick brown fox jumps over the lazy dog
    • ここで、「fox」が中心の単語だとすると、Skip-gramは「fox」から周辺の単語である「The quick brown」と「jumps over the lazy dog」を予測する
    • 中心の単語 → 周辺の単語
      • fox → (the, quick, brown, jumps, over, the, lazy, dog)

CBOWとSkip-gramの違い

  • 予測方法
    • CBOW：周辺の単語から中心の単語を予測
    • Skip-gram：中心の単語から周辺の単語を予測
  • 計算効率
    • CBOW：計算効率が高く、学習が高速
    • Skip-gram：計算効率は低いが、精度が高い
  • データ利用
    • CBOW：文脈全体を一度に利用して中心の単語を予測するため、大量のデータに対して適用しやすい
    • Skip-gram：一つの中心の単語から複数の周辺単語を予測するため、少量のデータでも高い精度が得られる

損失関数の工夫

課題として、コーパスが膨大となった場合
単語数分の損失を計算する必要が出てくる

損失関数の例（soft-max）

実際はほぼ負例なので、negative からいくつかもってくるnegative samplingで対応可能である

詳細は下記がわかりやすかった
https://qiita.com/g-k/items/69afa87c73654af49d36
https://note.com/smkt_interview/n/n71d4567d1096

kyo-dskyo-ds

RNN(再帰型ネットワーク)

RNNとは

  • RNN（リカレントニューラルネットワーク）は、時系列データやシーケンスデータの処理に特化したニューラルネットワーク。
  • 一般的なニューラルネットワーク（例えば、全結合層や畳み込み層）とは異なり、RNNは過去の情報を保持しながら現在の入力を処理することができる。
  • これにより、時間的な依存関係を考慮した処理が可能

RNNの挙動

通常のNNではそれぞれのインプットに対して独立で答えを出すが、
時系列的な情報を保有できない。

RNNでは再帰的に前層の情報を渡してあげるので、時系列的な要素を考慮できる。

RNNの具体的な挙動



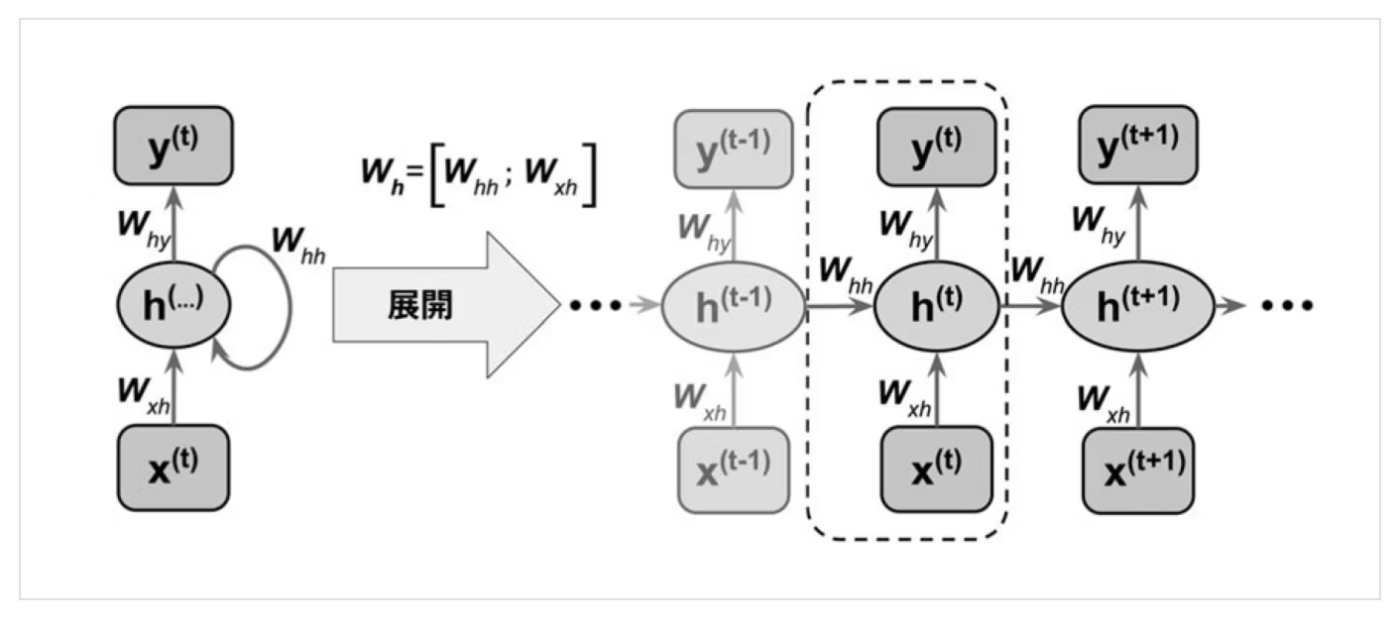
x(t)に前の層の隠れ層であるh(t-1)がconcatされたものがinputになり、h(t)を出力する。
その層のoutputはh(t)に重みをかけたものになる、それに対して損失計算する
次の層では、x(t+1)にh(t)をconcatしたものがinputになり、、の繰り返し！

誤差逆伝搬

誤差逆伝搬の図や式や複雑そうに見えるが、行列の掛け算、tanhなどの誤差逆伝搬を
落ち着体追えばそこまで難しいものではない。

https://ai.neoluxuk.com/index.php/Cat1No/A100/

BPTT

  • BPTTとは
    • BPTTはBackpropagation Through Timeの略
    • 上で紹介した再帰型のネットワークを、一本のネットワークに伸ばした形で表現し時間方向に誤差逆伝搬も行うというもの
  • BPTTの問題点
    • 長期時系列の問題を扱う場合に扱いづらい
      • 計算コストが大きい
      • 勾配が不安定、消失してしまう
  • 対策：Truncated BPTT
    • ネットワークのつながりを適当な長さで断ち切る
      • 小さなネットワークを複数作り、誤差逆伝搬を行う
      • ネットワークの逆伝搬のつながりだけを断ち切る（順伝播のつながりは残す）
        • 順伝播の入力はシーケンシャル（順番通り）に入力する
        • 逆伝搬はブロックで考える
    • ミニバッチ学習の場合は？
      • 各バッチでデータを与える開始位置をずらして学習順序を守った形で実装する
        1000個の長さの系列データで、10件区切りでtrucateし、バッチサイズ2で学習する場合の例が下記。
        開始位置を1と500でずらして学習を勧めていく点がポイント！

参考

https://www.youtube.com/watch?v=yvqgQZIUAKg

kyo-dskyo-ds

RNNの問題点への対応

RNNの問題点とは？

  • 長期依存性の課題
    • 長い文章を入力したときに、前半の記憶が薄れてあてにならない
  • 長期的な依存関係を学習するためには？
    • 勾配爆発
    • 勾配消失

勾配クリッピング

  • 勾配爆発に対する対策
  • 何をしているか
    • 逆伝搬の実行時に、勾配の上限を定める
  • 勾配クリッピングの手順

スキップ接続

  • 1層飛ばす（粗い時間スケールでの学習）
  • 勾配爆発の可能性は残る

leaky接続

  • 前時刻からの入力をα倍、入力層からの接続を1-α倍するような接続を持つ中間層をleakyユニット\
  • αが1に近ければ、過去の情報を長期間記憶する
  • αが0に近いならば、過去の情報は急速に破棄される
kyo-dskyo-ds

LSTM

LSTMとは

  • なぜLSTM??
    • RNNの問題点である勾配消失を解決するには根本的なアーキテクチャの変更が必要である
    • ここで"ゲート付きRNN"を導入する
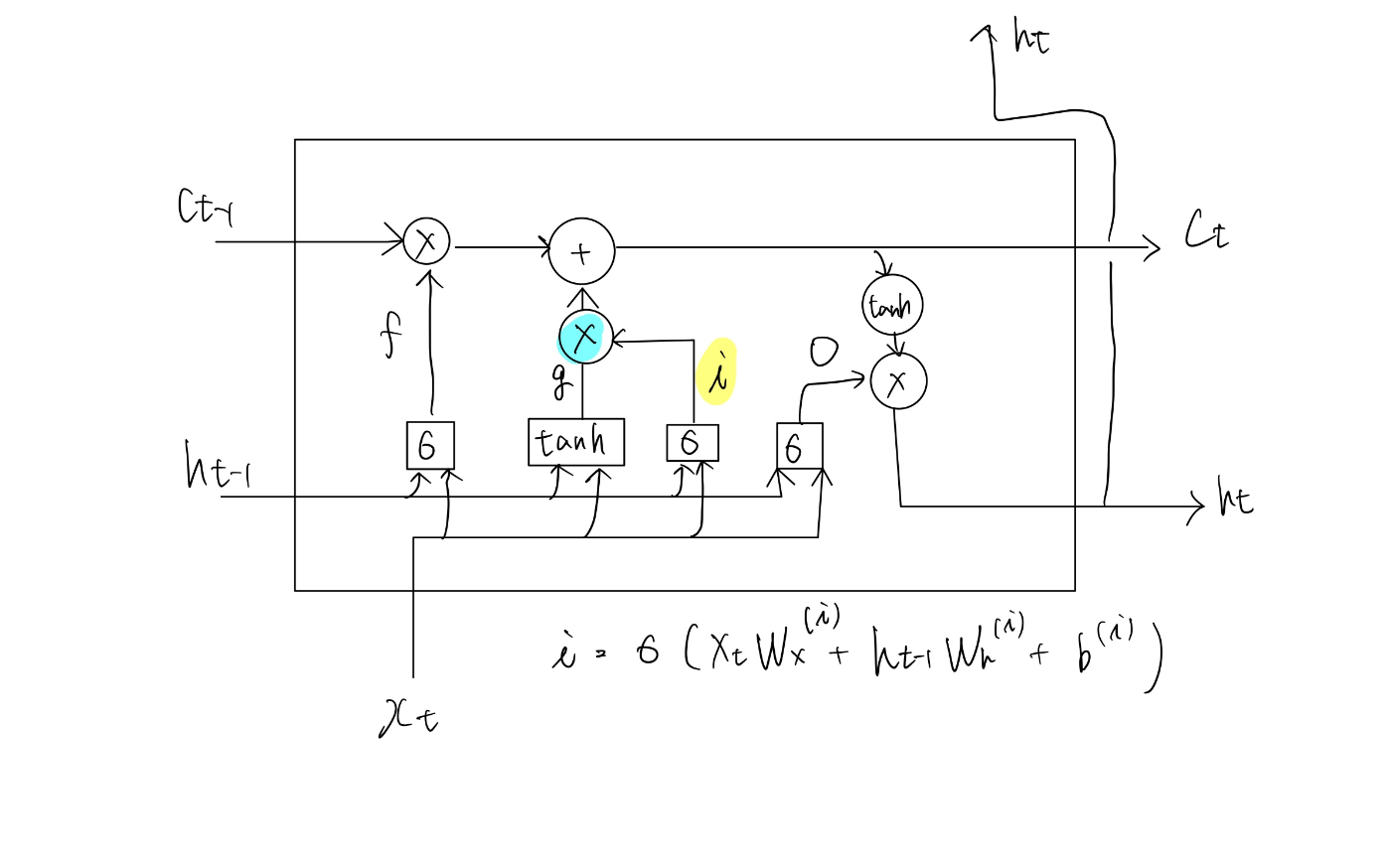
  • RNNとLSTMの違い

    大きな違いはLSTMにはcの経路があること
    Cは記憶セル と呼ばれ、LSTMの記憶部に相当する
    • 記憶セルの特徴
      • 自分自身（LSTMレイヤ内）だけでデータの受け渡しをする
      • LSTMレイヤ内だけで記憶の保持を完結できる
    • 隠れ状態hはRNNと同じく、別のレイヤ（上の方に抜ける）で出力される
    • つまり
      • LSTMの出力を受け取る側からみると、LSTMの出力は隠れ状態hのみで
        記憶セルcは出力されないため、その存在を考える必要はない

前提、注意点

  • 説明の簡略化のために下記のように表現を省略した形で、以後の議論や説明を進める

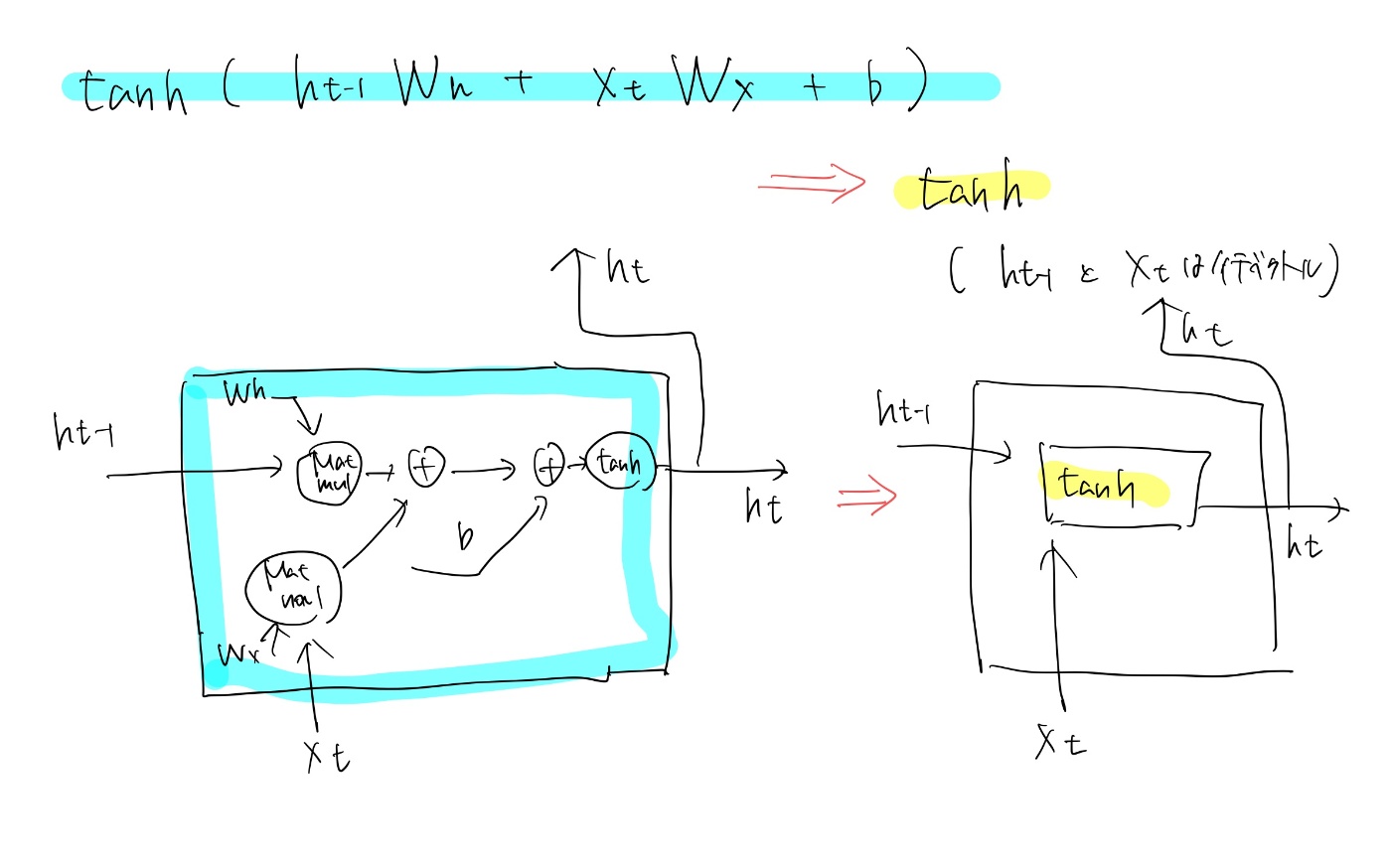
LSTMの組み立て

  • 記憶セルctには何が入っているか
    • 時刻tにおけるLSTMの記憶
    • 過去から時刻tまでの必要な情報すべてが格納されrている
  • どのようにLSTMは出力をするか
    • 記憶セルctの情報を下に、外部レイヤや次のLSTMレイヤに対して隠れ状態htを出力する
    • 出力は記憶セルをtanh関数で変換したものを出力する
  • cとｈの要素数
    • 記憶セルcと隠れ状態hの関係は要素ごとにtanhを適用しただけ
    • 要素数はcとhで等しくなる
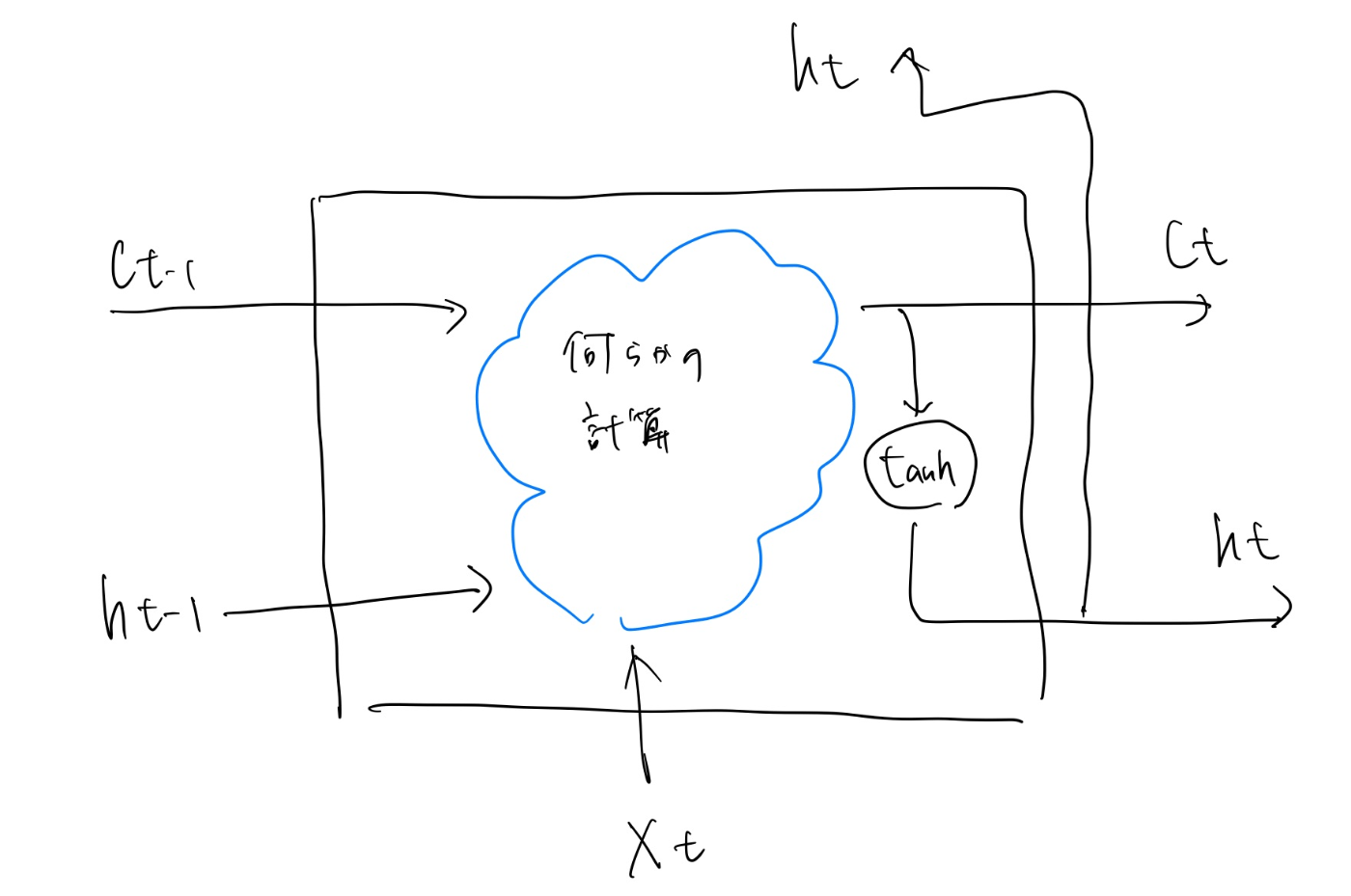
  • ゲートという概念
    • ゲートのイメージ
      • 水門をどれだけ開けるか？が直感的なイメージ
    • LSTMにおけるゲート
      • 開く/閉じるの二択でなく、どれだけ開けるか/閉じるかを定義する
      • 0.0~1.0の実数で表現される
      • ゲートの開き具体にはsigmoid関数がよく使われる
        • 値域が0-1なので

    outputゲート

    その出力が次時刻の隠れ状態としてどれだけ重要かを調整する
    • ここまでの、隠れ状態htは記憶セルctに対してtanhを適用しただけだった
    • それに対して、sigmoid関数を適用し、ゲートの要素を付け足す

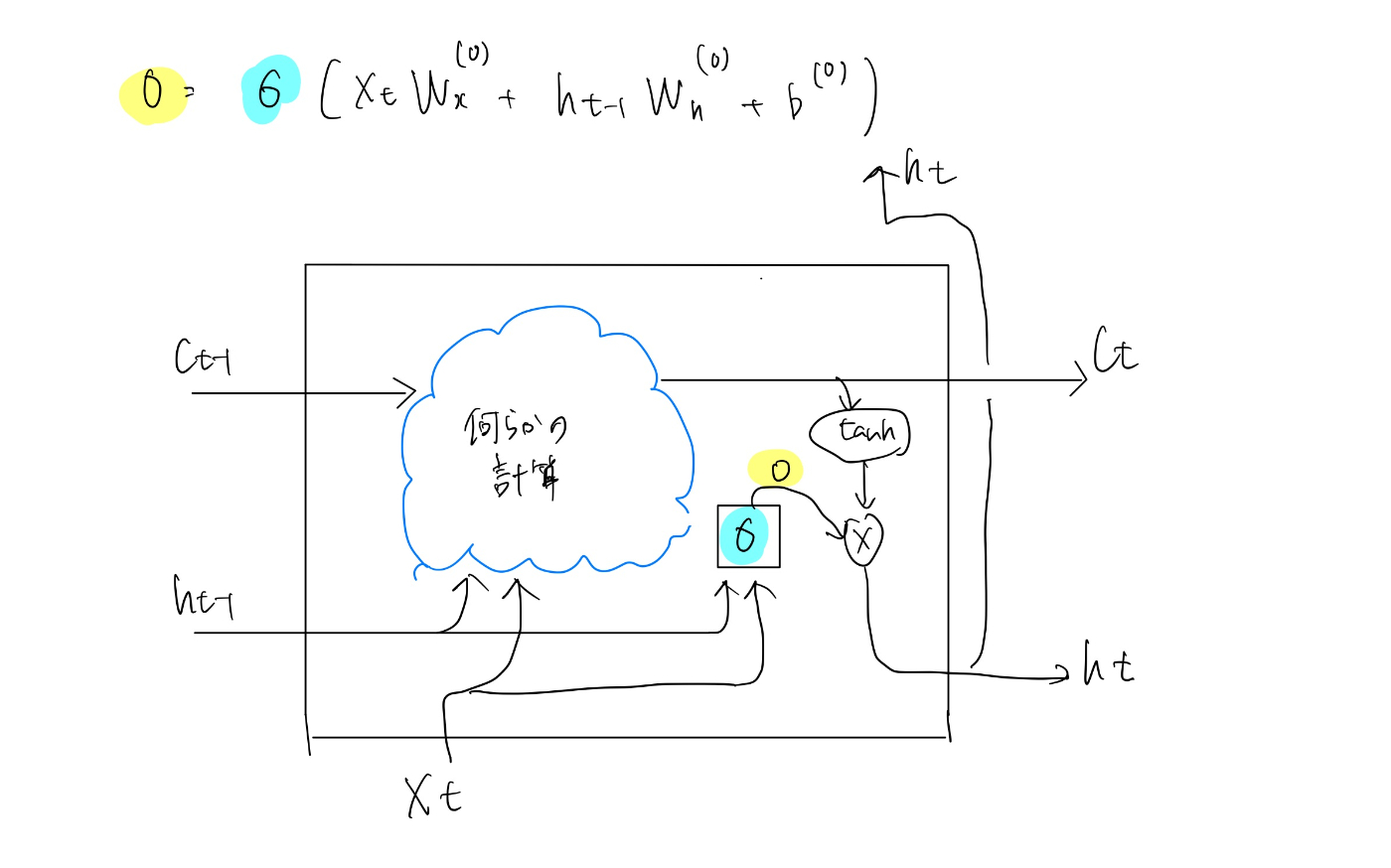
      htはoとtanh(ct)の積によって計算される。
      この積は要素ごとの積であり、アダマール積と呼ばれる。

forgetゲート

記憶セルに対して”何を忘れるか”を明示的に指示して上げる必要がある
ここでもゲートを利用する
ct-1の記憶から、不要な記憶を忘れるためのゲートを追加する（forgetゲート）

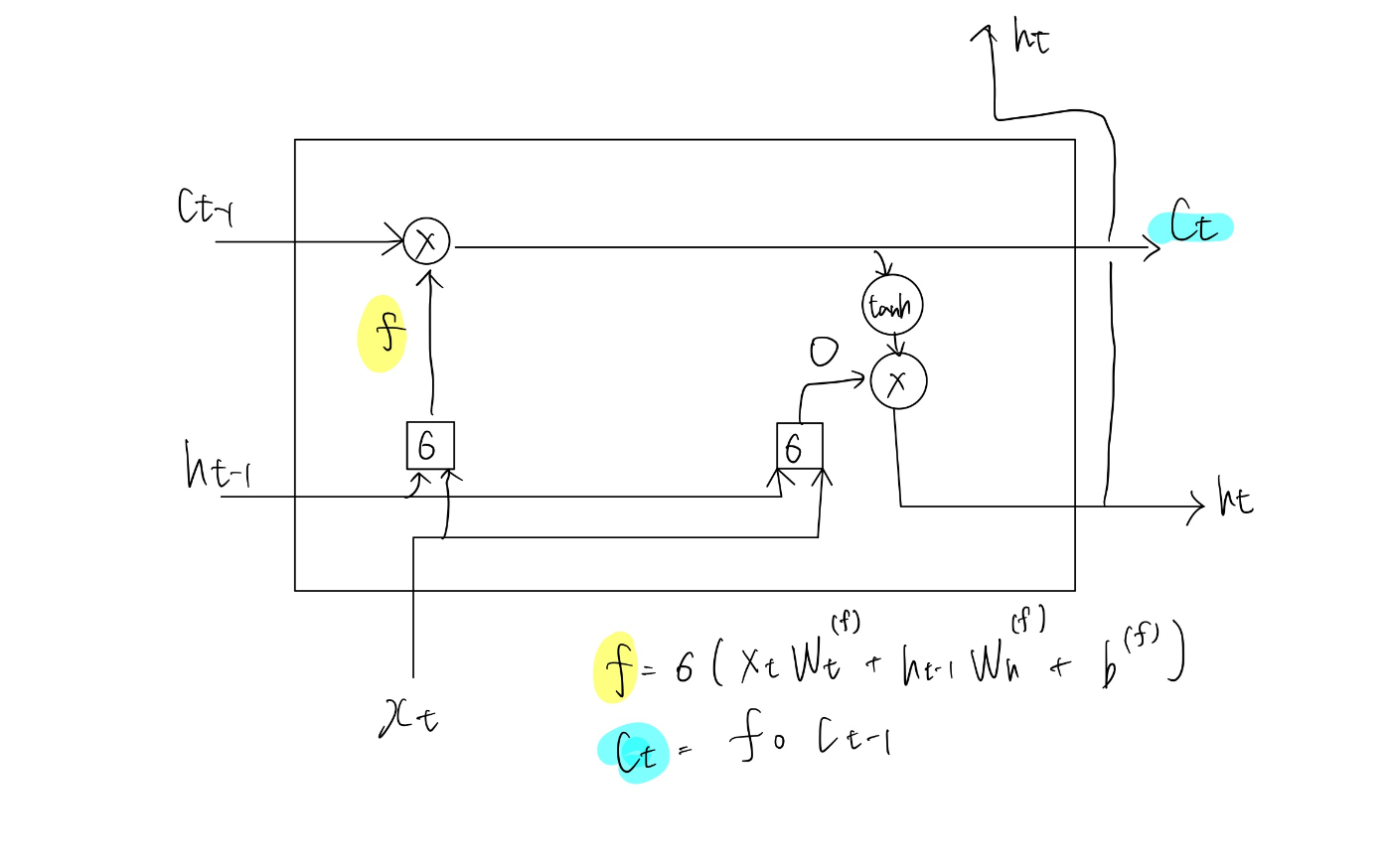
新しい記憶セル

forgetゲートの導入により、前時刻の記憶セルから忘れるべきものを削除できた。
しかし、このままでは記憶セルは忘れることしかできない。
新しく覚えるべき情報を記憶セルに追加する処理を加えていく。

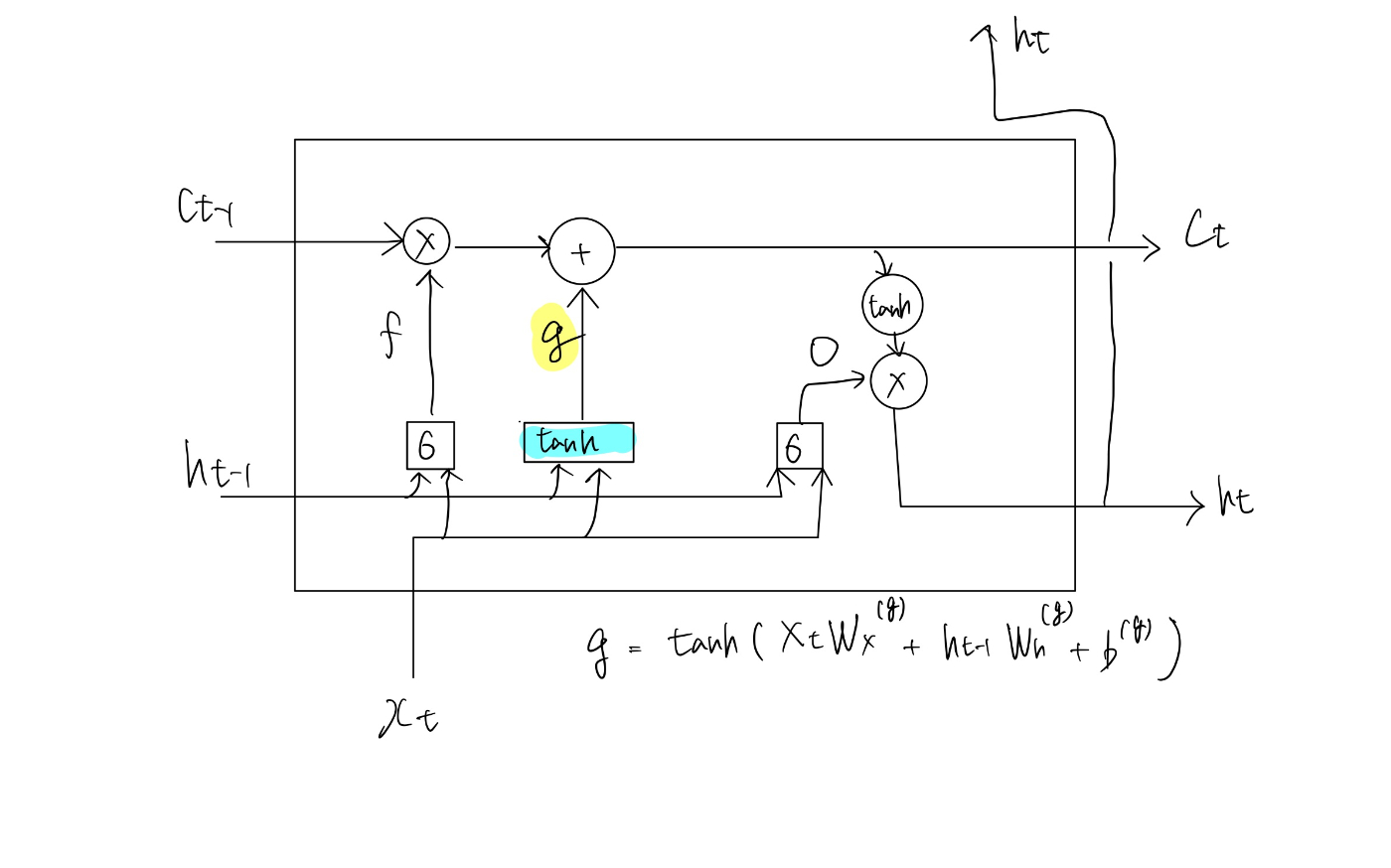
inputゲート

新しい記憶セルgに対してゲートを加える事を考える。
記憶セルにinputする割合を決めるゲートをinputゲートと呼ぶ。

kyo-dskyo-ds

GRU

LSTMの派生版

LSTMの問題点

  • LSTMはパラメータ数が多く、計算コストが高い
    →LSTMを簡略化したインターフェースのGRUが登場

GRUとは

  • GRUはLSTMの表現力を保ちつつ、計算コストを低くした
  • 残った機能
    • 隠れ状態に忘却機能と記憶機能を付与
      • 勾配消失が起きずらくなる
  • 失った機能
    • 忘却機能と記憶機能がトレードオフ
    • CECがなく、メモができない
      • 過去の情報が残りづらい

    GRUのアーキテクチャ

kyo-dskyo-ds

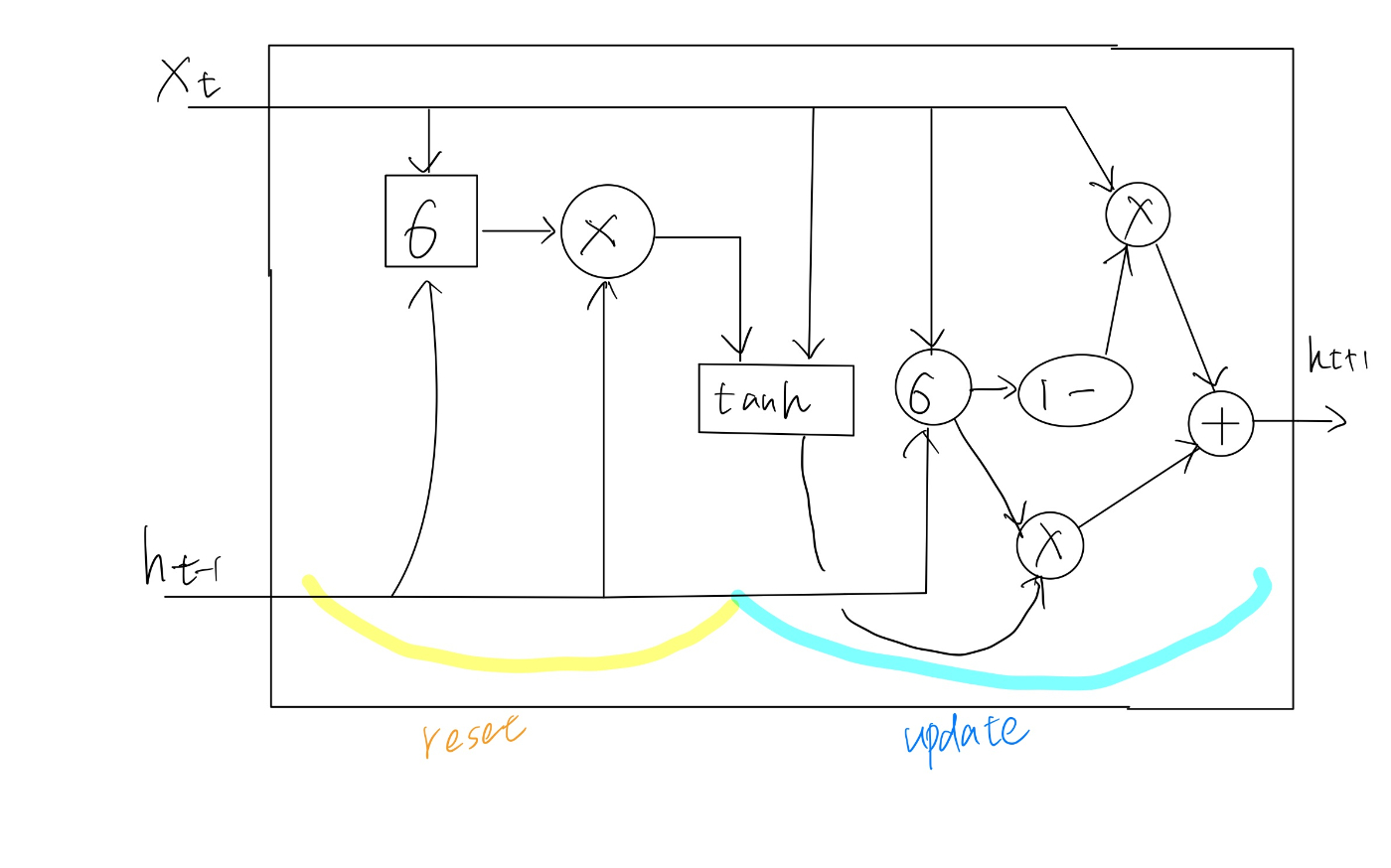
双方向RNN

順方向へ接続するRNNと逆方向へ接続するRNNを両方使い、結果をマージする

  • メリット
    • 例えば、英語を読むときに後ろから訳す場面はあり、
      機械も後ろからの文脈情報を知りたがっているので、逆方向のRNNも適用したらよいのでは？
kyo-dskyo-ds

CNN

畳み込みニューラルネットワーク（CNN）は、特に画像認識や画像分類の分野で非常に強力なツールである

畳み込みの基本概念

  • 畳み込み（Convolution）は、入力データとフィルタ（カーネル）を使って特徴を抽出する操作
  • 具体的には、入力画像に対して小さなフィルタをスライドさせて、フィルタと重なった部分の要素ごとの積和を計算します。この操作により、特定のパターンや特徴を強調する

フィルタ（カーネル）

  • フィルタは通常、3x3や5x5などの小さな行列で表される
  • 各フィルタは異なる特徴を捉えるために学習される
    • 例えば、エッジ検出やテクスチャの抽出など
  • カーネルは入力チャネル数分必要、特徴マップはカーネル適用後の出力を足し合わせたものになる

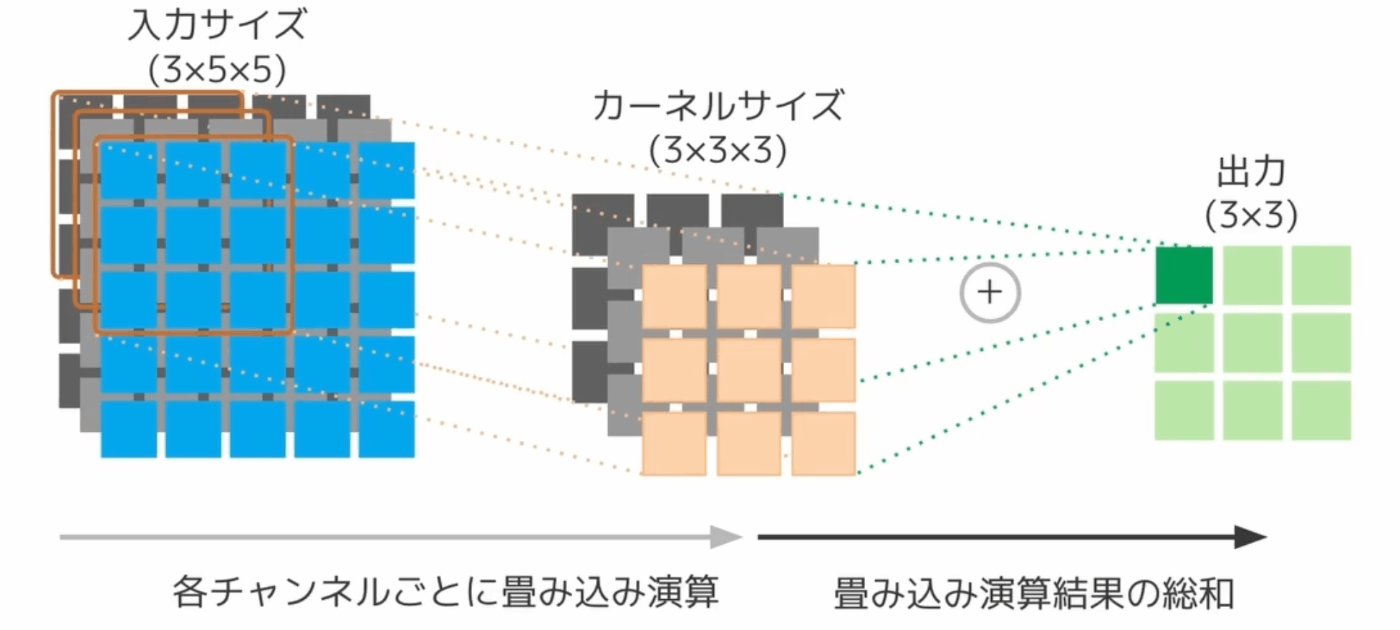
畳み込みの具体的なステップ

  1. 入力画像の準備：
    入力画像は通常、3次元のテンソル（高さ x 幅 x チャネル）で表されます。例えば、カラー画像であれば、チャネル数は3（RGB）です。

  2. フィルタの適用：
    フィルタ（カーネル）を画像の左上から右下へとスライドさせます。このとき、フィルタと重なる部分の要素ごとの積和を計算します。

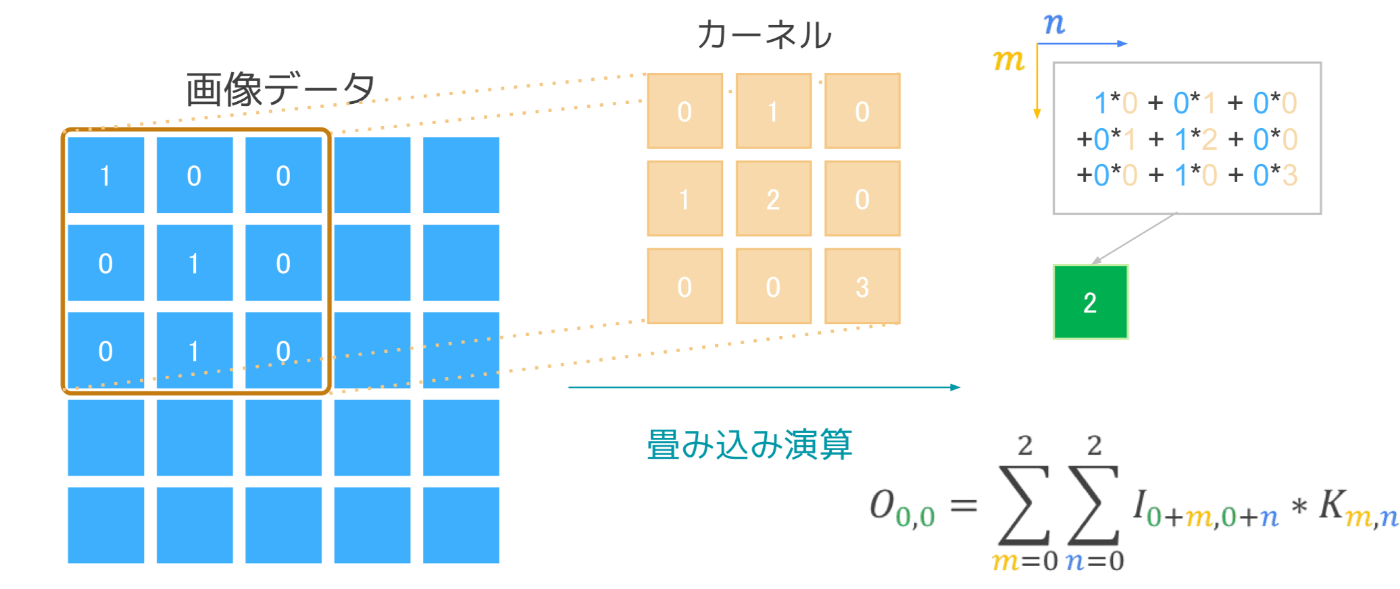
  3. ストライド（Stride）：
    フィルタをスライドさせるステップサイズです。ストライドが1の場合、フィルタは1ピクセルずつ移動します。ストライドが2の場合、2ピクセルずつ移動します。

  4. パディング（Padding）：
    入力画像の周りにゼロを追加して、フィルタが画像の端にも完全に適用されるようにします。これにより、出力画像のサイズを調整することができます。

    • ゼロパディング：ゼロを追加する。
    • 有効パディング：パディングなし。
kyo-dskyo-ds

特殊な畳み込みについて

CNNは便利かつ優秀な機能だが、計算コストが課題となる。
計算コスト抑えるためのいくつかの方法について紹介する

通常の畳み込み

  • チャンネル方向と平面方向に畳み込み演算を行う
  • フィルター次元数= (縦、横、チャネル数)

Pointwise Convolution

  • チャンネル方向のみの畳み込み
  • フィルター次元数=(1, 1, チャネル数)

Depthwise Convolution

  • 平面方向の畳み込み
  • フィルター次元数= (縦、横)

Depthwise Separable Convolution

pointwiseとdepthwiseを組み合わせて、畳み込みを実現する方法
計算コストを抑えられるなどのメリットがある。

利点

  1. 計算量の削減

    • 通常の畳み込み：フィルタサイズが3x3、入力チャネルが3、出力チャネルがNの場合、計算量は (3 * 3 * 3 * N)
    • Depthwise Separable Convolution：3つの3x3フィルタと3つの1x1フィルタを使用するため、計算量は(3 * 3 * 3 + 1 * 1 * 3 * N) となり、通常の畳み込みに比べて大幅に減少します。

  2. パラメータ数の削減

    • 通常の畳み込み：フィルタサイズが3x3、入力チャネルが3、出力チャネルがNの場合、パラメータ数は (3 * 3 * 3 * N)となる。
    • Depthwise Separable Convolution：3つの3x3フィルタ（計9個のパラメータ）と3つの1x1フィルタ（計3N個のパラメータ）を使用するため、パラメータ数は (9 + 3N) となり、通常の畳み込みに比べて大幅に減少します。

  3. メモリ効率の向上

    • 計算量とパラメータ数が減少することで、メモリ消費も減少します。これにより、モデルのトレーニングや推論時のメモリ使用量が削減されます。

  4. 速度の向上

    • 計算量が削減されるため、トレーニングと推論の速度が向上します。特にモバイルデバイスや組み込みシステムなどのリソースが限られた環境での応用に有利です。
kyo-dskyo-ds

CNNの概要

  • 入力画像に対して畳みこみ演算やプーリング処理を行なっていく
  • 畳み込みとは
    • 特徴量を抽出するフェーズ
    • シンプル、局所的な特徴量を抽出する
      • この部分にエッジがある、この部分が白っぽい
  • プーリングとは
    • 画像を圧縮し、複雑かつ大域的な情報を捉える
      • 白い花っぽい、細長い
kyo-dskyo-ds

プーリング

縦、横の空間を小さくする演算のことを指す

プーリングの例

  • 最大値プーリング
    • 各領域の最大値を取り出す
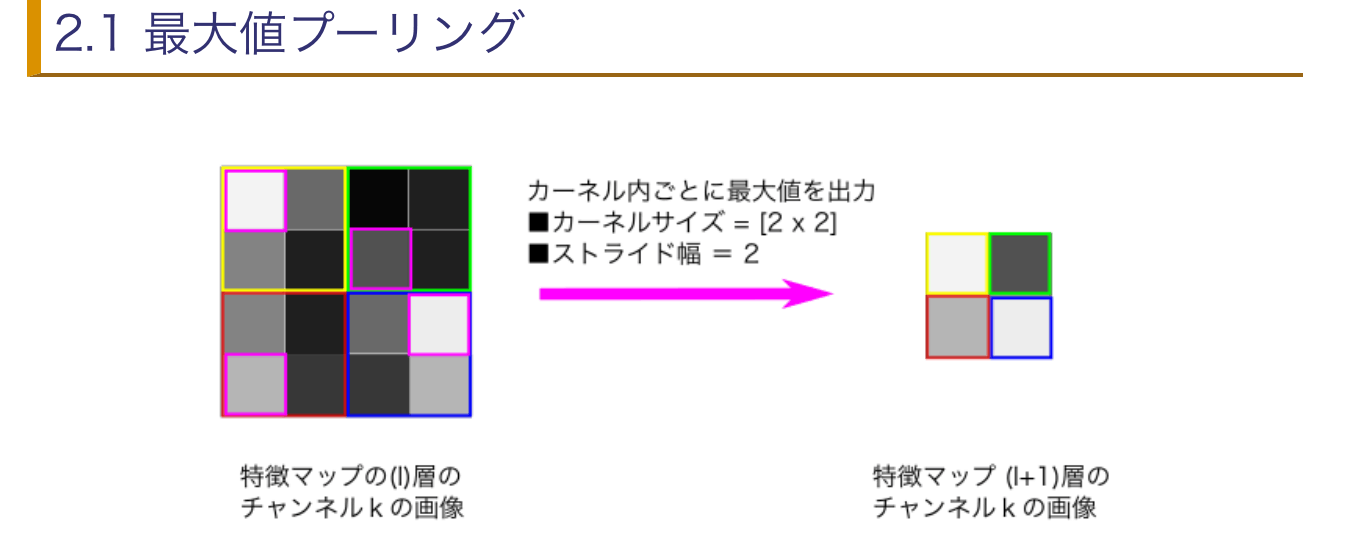
  • 平均値プーリング
    • 各領域の平均値を取り出す

プーリングのポイント

  • 学習するパラメータがない
    • 対象領域の最大値や平均値をとるだけなので学習するパラメータは存在しない
  • チャネル数が変化しない
    • チャネルごとに独立して計算が
  • 微小な変化に対してロバスト
    • 入力データの小さなずれをプーリングが吸収するので、入力データが横に１ピクセルだけずれた場合も出力は同じような結果となる。
kyo-dskyo-ds

im2col

image 2 columnの略で、画像を列形式に扱いやすくしましょうねという話。
CNNの畳み込み演算をそのまま実装すると、for文を複雑に組み合わせる必要があるが、numpyではfor文の処理が遅い課題がある
→入力とフィルターにim2colという関数を適用し、行列の内積を算出することで一気に畳み込み演算を行うという発想

im2colの仕組み

入力データを横方向の1行に、フィルターを縦方向で1列に展開して並べ、２つの行列の積を計算、出力データを適正な形状にreshapeする。
https://qiita.com/kuroitu/items/35d7b5a4bde470f69570

kyo-dskyo-ds

タスクの工夫

ワンショット学習

  • ラベル付きデータを一つだけ与えて学習する
  • ラベルなしで潜在的なクラスを分ける
  • 例）顔画像を1例入力し、どの方向を向いた顔でも認識できるよう学習

ゼロショット学習

  • ゼロショット学習の基本的なアイデア
    • 既知のクラスと未知のクラスの間に共通の特徴や属性を利用して、新しいクラスを予測
    • 既知の情報のベクトルとの距離を利用する

半教師あり学習

教師あり学習を拡張し、一部データのみラベルありのデータセットを学習すること

self-training

  1. ラベルがついたデータで学習しモデル作成
  2. ラベルなしデータを推論
  3. 信頼度が高いデータにはラベルを付け、再度データを増やして学習する

co-training

流れはself-trainingと同等だが、2のフェーズでアンサンブルモデルを用いる

マルチタスク学習

１つのモデルで複数のタスクを同時にこなせるように学習することで、メインタスクの汎化性能の向上を目指す

能動学習

アノテーションの半自動化を行う
モデルが自動でラベル付けを行うが、一部人間が担当する

  • 分類を人間に手伝ってもらう場合のデータの選び方
    • ucertainly sampling
      • 自身がないデータのアノテーションを人間に任せる
    • diversity sampling
      • データの分布を代表するような点を取り出してアノテーションを人間にさせる

距離学習

  • 距離学習（Metric Learning）は、データポイント間の距離や類似度を学習する手法です。距離学習の主な目的は、データポイントを埋め込み空間にマッピングし、その空間内で類似のデータポイントが近く、異なるデータポイントが遠くに配置されるようにすることです。これにより、分類やクラスタリング、検索などのタスクが容易になります。
  • 具体例
    • 顔認識のタスクで、距離学習を利用する。
    • 同一人物の顔画像は埋め込み空間内で近くに配置され、異なる人物の顔画像は遠くに配置されるように学習できます。これにより、新しい顔画像が追加された際にも、モデルは類似度に基づいて正確に認識することができます

Siamese network

同じネットワークを2つ使用して、入力データペアを処理し、それぞれの出力埋め込みを比較します。出力埋め込み間の距離が近いほど、入力データペアが類似しているとみなす。
例: 顔認識タスクで、同一人物の顔画像ペアに対して出力埋め込みが近くなるように学習

  • 学習手順
    1. データセットから２つの入力のペアセット（xi, xj)を作る
    2. ペアを同一のNetworkに入れ、出力(yi, yj)を計算
    3. その出力とペアの類似性 t を使って損失関数を計算し学習
    4. 23を繰り替えす

Triplet Network

Tripletはランダムに3つの入力ペアを作成

  • 入力の種類
    • 基準サンプル（アンカー）
    • 正例（ポジティブ）
    • 負例（ネガティブ）
  • アンカーとポジティブの距離、アンカーとネガティブの距離を２種類求め
    損失関数を計算する

Siamese と Tripletの比較

  • Tripeletのほうがラベル間を離そうとする力が強い
  • TripeletはSiameseに比べ、positiveとnegativeを必ず用意するので
    近づけることと離すことをバランスよくできる。
  • ペアの作り方次第ではSiameseに比べてよい精度が出る可能性もあり、ペアを作るサンプリングにも議論の余地がある。
kyo-dskyo-ds

Batch Normalization

バッチ方向にデータ正規化する。
ベクトルXをd次元のベクトルと考えると、あるj次元のベクトルに対して
バッチ方向に平均や分散をとり、データの次元数ごとにスケーリングする

バッチ正規化の概要

バッチ正規化は、ニューラルネットワークの各層の出力を正規化し、スケーリングとシフトを行う技術です。これにより、学習の効率を高め、ネットワークの安定性を向上させることができます。バッチ正規化は2015年にS. IoffeとC. Szegedyによって提案され、その後、多くのディープラーニングモデルで広く採用されています。

バッチ正規化のメリット

  1. 勾配消失・勾配爆発の問題の緩和
    バッチ正規化は各層の出力を正規化することで、入力データのスケールを均一に保ちます。これにより、勾配が極端に小さくなったり、大きくなったりする「勾配消失」や「勾配爆発」の問題を緩和し、より安定した学習が可能になります。
  2. 学習速度の向上
    バッチ正規化を使用することで、大きな学習率（learning rate）を使用しても安定した学習が可能になります。これにより、学習の収束速度が向上し、トレーニング時間が短縮されます。
  3. 初期化の依存性の軽減
    バッチ正規化はネットワークの重みの初期化に対する依存性を軽減します。これにより、初期化の影響を受けにくくなり、異なる初期化方法でも安定した学習が期待できます。
  4. 過学習の抑制
    バッチ正規化はミニバッチごとにデータを正規化するため、トレーニング時にランダムなノイズが導入されます。これが一種の正則化（Regularization）効果を持ち、過学習を抑制するのに役立ちます。
  5. モデルの汎化性能の向上
    バッチ正規化の正則化効果により、モデルの汎化性能（generalization performance）が向上します。これは、テストデータや実際のデータに対しても高い精度を維持することができるという意味です。

kyo-dskyo-ds

Layer Normalization

方向性：
レイヤー正規化は「レイヤー方向」に沿って平均と分散を計算します。すなわち、各データポイントの全次元に対して計算を行います。

適用場所：
レイヤー正規化はバッチ正規化の代替として提案され、特にリカレントニューラルネットワーク（RNN）や自然言語処理（NLP）のタスクで効果的です。各データポイントごとに統計量を計算し、その後に正規化とスケーリング・シフトを行います。

メリット：
ミニバッチサイズに依存せず、バッチサイズが1の場合でも効果を発揮します。
バッチ正規化と異なり、トレーニング時と推論時で動作が同じです。

欠点：
バッチ正規化に比べて学習速度が遅くなる場合があります。
勾配消失・勾配爆発の問題に対する効果はバッチ正規化ほど強力ではありません。

kyo-dskyo-ds

VAE

VAEとは？

まず、オートエンコーダ（Autoencoder）というのは、入力データを圧縮して（エンコード）、その圧縮されたデータから元のデータに復元（デコード）するためのニューラルネットワークです。VAEはこのオートエンコーダをちょっと賢くしたものです。

例えるならば…

オートエンコーダを「普通のカメラ」と考えてください。このカメラは写真を撮って、その写真をデジタルデータとして保存し、再びそのデータから写真を表示します。
一方、VAEは「予測機能付きのカメラ」です。このカメラは、写真を撮って保存するだけでなく、その写真がどんな風景かを予測して、似たような新しい写真を生成することもできます。

VAEの仕組み

エンコーダ（Encoder）：

エンコーダ部分は、入力データを圧縮して「潜在変数（latent variables）」と呼ばれる少数の変数に変換します。これが普通のオートエンコーダと同じ部分です。 しかし、VAEではこの潜在変数を「確率分布」として表現します。つまり、ただ1つのデータポイントに圧縮するのではなく、データがどのような範囲に存在するかを示します。

リパラメータトリック（Reparameterization Trick）：

確率分布を使って潜在変数をサンプリング（抽出）します。このステップがVAEの特殊な部分で、簡単に言うと「変数をランダムに選ぶ」ことです。

デコーダ（Decoder）：

デコーダ部分は、サンプリングされた潜在変数から元のデータを再構成します。これにより、新しいデータを生成することもできます。例えば、新しい画像や新しいテキストを生成することができます。

VAEのメリット

データ生成：
VAEは新しいデータを生成する能力があります。例えば、顔写真のデータセットを学習したVAEは、新しい顔写真を生成できます。
データの圧縮：
データを有効に圧縮し、潜在変数として保存することができます。これにより、重要な情報を少数の変数にまとめることができます。

VAEの損失関数ってなに？

VAEの損失関数の構成

VAEの損失関数は、大きく分けて2つの部分から構成されています：

KLダイバージェンスでエンコーディング後の分布と、事前分布の正規分布を比較する理由は？

kyo-dskyo-ds

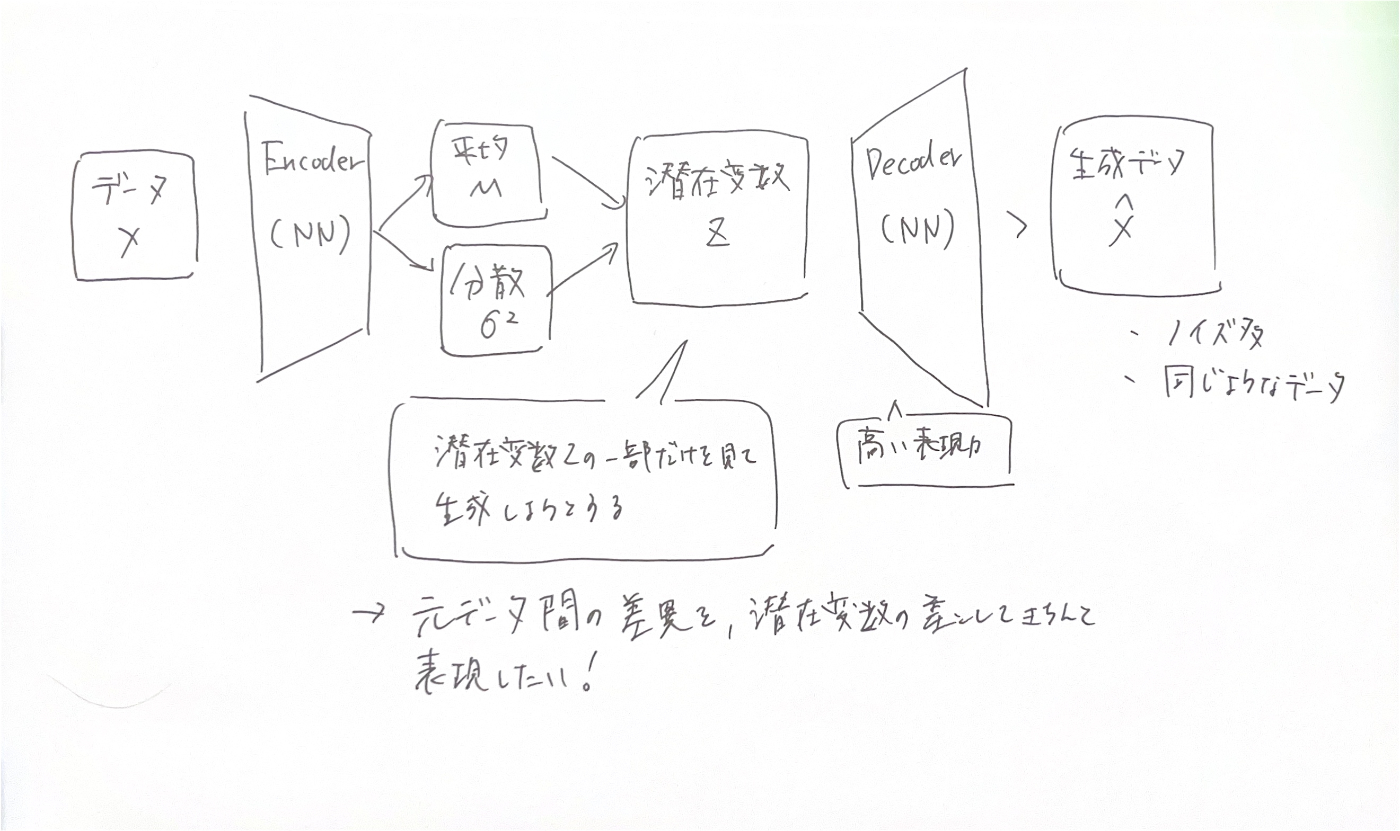
VAEの課題

posterior collapse

PixelCNNなどの高い表現力がある、Decoderを使うときに潜在変数を無視した生成が行われてしまう現象

VQ VAE

潜在変数をVAEの時と異なり、離散的なベクトルとして扱う
VAEでは連続と仮定していたが、本来文章や画像は離散的なため。

kyo-dskyo-ds

マルチヌーイ分布とは？

定義

標本空間

\Omega = \{x_1, x_2, \dots, x_k\}

のように 事象が k 種類ある試行 を マルチヌーイ試行 と呼びます。

マルチヌーイ分布（カテゴリカル分布）は、確率変数 X がマルチヌーイ試行に従うときの 確率分布 です。

確率質量関数（PMF）

確率質量関数 f_X(x; p) は次のように表されます：

f_X(x; p) = \prod_{i=1}^k p_i^{x_i}
  • x = (x_1, x_2, \dots, x_k)^\top は one-hot ベクトル
  • p = (p_1, p_2, \dots, p_k)^\top は確率ベクトル（各クラスの確率）

制約条件

  • \sum_{i=1}^k x_i = 1
  • \sum_{i=1}^k p_i = 1, 各 p_i \in [0, 1]

例：サイコロ

サイコロの出る目を1〜6としたとき、各面の確率は等しく：

p = (p_1, p_2, p_3, p_4, p_5, p_6) = \left(\frac{1}{6}, \frac{1}{6}, \frac{1}{6}, \frac{1}{6}, \frac{1}{6}, \frac{1}{6}\right)

出目が「1」の場合、one-hot ベクトル X は：

X = (1, 0, 0, 0, 0, 0)

このときの確率質量関数は：

f_X(x; p) = \prod_{i=1}^6 p_i^{x_i} = \frac{1}{6}

補足：ベルヌーイ分布との関係

k = 2 のとき、マルチヌーイ分布は ベルヌーイ分布 と一致します。

f(x) = p^x (1 - p)^{1 - x}

参考リンク

kyo-dskyo-ds

尤度とは？

尤度の直感

特定のデータ x が観測されたとき、
それがある確率モデル \theta の下でどれほどもっともらしいか
→ それを表すのが「尤度（Likelihood）」！

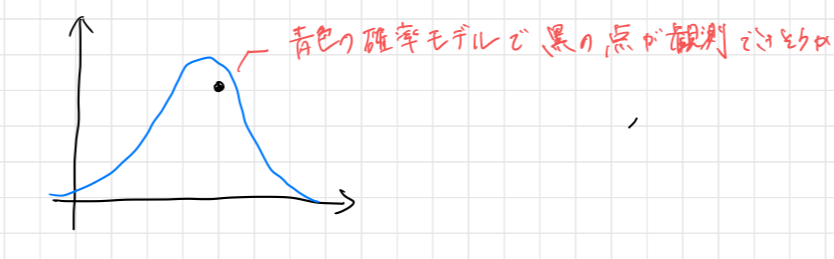
概念図

  • 青い曲線：確率モデル（例：正規分布）
  • 黒い点：観測データ点
    → 「この点はこのモデルで生成されそうか？」を評価するのが尤度

確率と尤度の違い

観点 確率（Probability） 尤度（Likelihood）
対象 データの発生確率 パラメータの尤もらしさ
形式 P(X = x \mid \theta) L(\theta \mid x)
パラメータ 固定されている データが固定されている
主な用途 モデルからデータを生成 データからモデルを当てる（推定）

数式で理解する尤度関数

例題（ベルヌーイ分布）

ベルヌーイ分布に従うデータ x_1, x_2, ..., x_n があるとします。
確率質量関数は：

f(x_i; p) = p^{x_i}(1 - p)^{1 - x_i}

それらのデータが同時に観測される確率（尤度関数）は：

L_D(p) = \prod_{i=1}^n f(x_i; p) = \prod_{i=1}^n p^{x_i}(1 - p)^{1 - x_i}

尤度関数とは？

確率関数にデータの各値を代入して積をとったもの。

最尤推定（MLE）

最も尤もらしいパラメータを見つけるため、尤度関数を最大化する：

\hat{p} = \arg \max_p L(p)

対数尤度

尤度関数はたくさんの確率の積なので、値がとても小さくなる。
そのため、計算しやすくするために対数をとる：

\log L_D(p) = \sum_{i=1}^n \left[ x_i \log p + (1 - x_i) \log(1 - p) \right]

ポイントまとめ

  • 確率：パラメータが固定 → データの確率を求める
  • 尤度：データが固定 → どのパラメータが最もらしいかを評価
kyo-dskyo-ds

正規分布・標準正規分布・Zスコアとは？

1. 正規分布（Normal Distribution）とは？

正規分布は、平均 \mu、分散 \sigma^2 の連続確率分布であり、多くの自然現象（身長、テストの点数、誤差分布など）を記述できます。

確率密度関数（PDF）

f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right)
  • \mu：平均（中心の位置）
  • \sigma：標準偏差（広がり具合）
  • 分布の形は左右対称な「釣鐘型」

2. 標準正規分布（Standard Normal Distribution）

正規分布の特別なケースであり、以下のように定義されます：

  • 平均 \mu = 0
  • 分散 \sigma^2 = 1

標準正規分布のPDF

\phi(z) = \frac{1}{\sqrt{2\pi}} \exp\left( -\frac{z^2}{2} \right)

これを基準に他の正規分布を比較するため、「標準化」が行われます。

3. Zスコア（Z-score）とは？

Zスコアとは、ある値が「平均からどれくらい離れているか」を標準偏差単位で表す指標です。

Zスコアの定義式

z = \frac{x - \mu}{\sigma}
  • x：観測値
  • \mu：平均
  • \sigma：標準偏差

Zスコアの意味

Zスコアは、元の正規分布を標準正規分布へ変換する操作です。

X \sim \mathcal{N}(\mu, \sigma^2) \quad \Rightarrow \quad Z = \frac{X - \mu}{\sigma} \sim \mathcal{N}(0, 1)

4. Zスコアの実用例

例1：偏差値の計算

偏差値はZスコアを元にして次のように定義されます：

\text{偏差値} = 10z + 50 = 10 \cdot \frac{x - \mu}{\sigma} + 50

→ 平均 50・標準偏差 10 に変換したスコア。

例2：異常検知（Anomaly Detection）

Zスコアの絶対値が大きい（例：|z| > 3）ような観測値は「統計的に異常」とみなされることがあります。

  • 通常：z \in [-2, 2] に約95%のデータが含まれる
  • |z| > 3：1%以下の稀な値

例3：確率の計算

Zスコアを使うことで、任意の正規分布の確率を標準正規分布表（Z表）から求めることができます。

例：X \sim \mathcal{N}(170, 10^2) のとき
P(X \leq 185) を求めたい：

z = \frac{185 - 170}{10} = 1.5

Z表より：P(Z \leq 1.5) \approx 0.9332

5. まとめ

概念 意味 数式 特徴
正規分布 任意の平均・分散の分布 \mathcal{N}(\mu, \sigma^2) 現実の現象をよく近似
標準正規分布 \mu=0, \sigma=1 の正規分布 \mathcal{N}(0, 1) Zスコアで変換される
Zスコア 平均からのずれを標準化 z = \frac{x - \mu}{\sigma} 比較・確率計算・異常検知
kyo-dskyo-ds

正規分布と最尤推定の関係

1. 正規分布の確率密度関数（PDF）

平均が \mu、分散が \sigma^2 である正規分布 \mathcal{N}(\mu, \sigma^2) の確率密度関数は、以下の式で表されます：

f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{1}{2\sigma^2}(x - \mu)^2 \right)

この分布は左右対称な釣鐘型をしており、自然界のさまざまな現象に適用されます。

2. 最尤推定と二乗和誤差の関係

正規分布をモデルとしたとき、最尤推定（MLE）によって平均 \mu を求める操作は、二乗和誤差（Squared Error）を最小化する操作と一致します。

これは以下のように表現されます：

\mu_{\text{MLE}} = \arg\min_{\mu} \sum_{i=1}^n (x_i - \mu)^2

すなわち、最尤推定の結果として得られる平均値は、「観測データに最も近い」とされる平均点です。

3. 最尤推定量は「標本平均」になる

正規分布の平均 \mu に対する最尤推定量は、観測データの単純な平均で与えられます：

\hat{\mu}_{\text{MLE}} = \frac{1}{n} \sum_{i=1}^n x_i

これは「標本平均（sample mean）」と一致し、非常に直感的かつ重要な性質です。

✔ ポイントまとめ

  • 正規分布の PDF は指数関数と平方項で構成される
  • 最尤推定と二乗誤差最小化は数学的に同じ目的関数
  • 平均の最尤推定値はデータの平均そのものになる

🧪 試験対策Tips

  • 正規分布に従うデータの平均を推定するとき、「最尤推定＝平均値」と覚えておくと便利
  • MSE（Mean Squared Error）と正規分布の最尤推定は密接な関係がある

よくある二乗誤差を最小化するというのは、誤差が正規分布に基づくという仮定があれば有効である。
二乗誤差の最小化は簡単な問題だと解析的に解ける。よくあるのは最小二乗法ですね、振り子の実験のやつ
https://manabitimes.jp/math/942

kyo-dskyo-ds

ベイズの識別規則

✅ ベイズの定理と識別問題

ベイズの定理は、「観測データが得られたとき、そのデータが特定のクラスに属している確率（事後確率）」を求めるための公式です。

🔢 数式（ベイズの定理）

P(C_k \mid x) = \frac{P(x \mid C_k) \cdot P(C_k)}{P(x)}
項目 意味
C_k クラス（例：健康 or 病気）
x 観測データ（例：喫煙・飲酒の有無）
P(C_k) 事前確率：クラス C_k の出現確率
P(x \mid C_k) 尤度：クラス C_k においてデータ x が得られる確率
P(x) 周辺確率（全体の平均的な出現確率）
P(C_k \mid x) 事後確率：データ x が得られたときに C_k に属する確率

🧪 具体例：健康アンケート

集計データ

喫煙＆飲酒あり その他 合計
健康 320人 480人 800人
健康でない 160人 40人 200人
合計 480人 520人 1000人

喫煙かつ飲酒している人が「健康」である確率は？

ベイズの定理を用いると：

  • 事前確率（健康である）：

    P(\text{健康}) = \frac{800}{1000} = 0.8

  • 尤度（健康な人のうち喫煙・飲酒する確率）：

    P(x \mid \text{健康}) = \frac{320}{800} = 0.4

  • 周辺確率（喫煙・飲酒者全体の割合）：

    P(x) = \frac{320 + 160}{1000} = 0.48

  • よって、事後確率は：

    P(\text{健康} \mid x) = \frac{0.4 \cdot 0.8}{0.48} = \frac{0.32}{0.48} = 0.666...

➡️ 喫煙・飲酒している人が「健康」である確率は約 66.7%

⚖️ 損失の考慮（リスクベース判断）

ベイズ識別では「事後確率が最大のクラスを選ぶ」のが基本ですが、**判断ミスに対する損失（コスト）**を加味すると選択が変わることがあります。

例：

  • 病気の人を「健康」と誤判定する損失は大きい
  • 健康な人を「病気」と誤判定する損失は小さい

損失行列を定義：

実際＼判定 健康 病気
健康 0 1
病気 10 0

このとき、損失の期待値を以下で計算：

  • 健康と判定した場合：

    L_{\text{健康}} = 0 \cdot 0.666... + 10 \cdot 0.333... = 3.33

  • 病気と判定した場合：

    L_{\text{病気}} = 1 \cdot 0.666... + 0 \cdot 0.333... = 0.666...

➡️ 損失の期待値が小さい方、**つまり「病気」**と判定するのが合理的。

🚫 判断のリジェクト（棄却）

事後確率がどちらも高くない場合、「判断を棄却する」選択肢を導入できる。
確率の最大値がある閾値 \delta より小さいときには分類せず「わからない」と判定する。

例：

  • P(C_1 \mid x) = 0.51
  • P(C_2 \mid x) = 0.49
  • \delta = 0.6 のとき → リジェクト

このように、確信度が低い場合に分類を避ける仕組みを導入できる。

参考
https://manabitimes.jp/math/1390

kyo-dskyo-ds

モンテカルロ積と交差エントロピーの関係

交差エントロピーは、分類モデルの損失関数としてよく使われます。
一方、モンテカルロ法（モンテカルロ積）は、積分をランダムサンプリングで近似する手法です。

交差エントロピーとは？

交差エントロピーは、真の分布 p(x) とモデルの予測分布 q(x) のズレを測る指標。定義は以下のとおり：

H(p, q) = -\int p(x) \log q(x) \, dx

モデルが正解に自信を持っていれば損失は小さく、外していれば大きくなります。

モンテカルロ積とは？

モンテカルロ積は、積分をサンプリングで近似する方法です。
例えば：

\int f(x) \, dx \approx \frac{1}{N} \sum_{i=1}^N f(x_i) \quad (x_i \sim \text{some distribution})

このように、「関数の平均値 ≒ ランダムサンプルの平均値」として積分を近似します。

モンテカルロで交差エントロピーを近似する

交差エントロピーも積分なので、サンプル x_i \sim p(x) を使ってこう近似できます：

H(p, q) \approx -\frac{1}{N} \sum_{i=1}^N \log q(x_i)

これは、真の分布から得られたデータに対して、モデルの出した確率の log を平均する、という意味です。

2クラス分類での形

2クラス分類（例：猫 or 犬）では、ラベル y_i \in \{0, 1\}、予測値 q_i = P(y=1 \mid x_i) としたとき、交差エントロピー損失は：

H(p, q) = -\frac{1}{N} \sum_{i=1}^N \left[ y_i \log q_i + (1 - y_i) \log (1 - q_i) \right]
  • 正解が 1 の場合： -\log q_i
  • 正解が 0 の場合： -\log (1 - q_i)

この2つのケースを1つの式にまとめた形です。

多クラス分類との違い

多クラス分類では、正解ラベルがクラスインデックス（例：2）として与えられ、モデルの出力 q_i は各クラスの確率ベクトルになります。

損失は以下のように「正解クラスだけ」に着目して計算します：

H(p, q) = -\frac{1}{N} \sum_{i=1}^N \log q_{i, y_i}

まとめ

観点 説明
交差エントロピー 真の分布と予測分布のズレを測る損失（積分で定義）
モンテカルロ積 積分をサンプルの平均で近似する方法
関係性 データセットをサンプルと見なすと、損失の計算はモンテカルロ積と一致する
2クラス分類の損失 正例と負例の両方の log を含む形
多クラス分類の損失 正解クラスだけに log を取る形
kyo-dskyo-ds

🔍 MLEとベイズ推定のちがいを感覚で理解する

✅ まず両者に共通する「尤度」とは？

観測データがあったときに「このパラメータ（仮説）なら、どれくらいありそうか？」を評価する関数。

つまり、観測データを基にパラメータの“もっともらしさ”を測る道具が「尤度（likelihood）」です。

💡 感覚的なイメージ：犯人捜しに例えると？

🎯 最尤推定（MLE）

  • データ（事件）はもう起こった事実。
  • その事実をもとに、どの犯人（パラメータ）が一番それっぽいかを探す。
  • 答えは1つ（点推定）。

🔍「この事件を起こしたのは、誰だ？」

📊 ベイズ推定

  • 事件は起こったが、犯人の情報はぼんやりしている。
  • そこで「証拠（データ）」を新たに得て、犯人の可能性（パラメータの確率分布）をアップデートする。
  • 確率分布として“疑わしさ”を扱う。

🔁「新しい証拠をもとに、怪しい人物リストを更新しよう」

✅ 数式で整理すると…

観点 最尤推定（MLE） ベイズ推定
尤度の役割 主役：最大化の対象 脇役：事後分布の構成要素
数式 \hat{\theta}_{\mathrm{MLE}} = \arg\max_{\theta} P(x \mid \theta) P(\theta \mid x) = \frac{P(x \mid \theta) \cdot P(\theta)}{P(x)}
出力 点推定（犯人はこの人！） 分布（誰が怪しいかのスコア表）
特徴 シンプル・高速・過学習しやすい 事前知識も反映・安定しやすい

🤔 なんで混乱するの？

最尤推定とベイズ推定では、同じ「尤度」を使っているのに、どちらが主役か・何を最大化しているかが違うからです。

  • MLE：尤度だけを見る → 最大化して「1つの答え」を出す
  • ベイズ：尤度×事前分布 → 更新して「確率分布」を出す

🧠 バカでもわかるひとこと解説（覚え方）

用語 覚え方
尤度（likelihood） 「この証拠はこの犯人にとってどれくらい自然か？」
MLE 「証拠から一番怪しい奴を選ぶ」
ベイズ推定 「疑わしさランキングを日々アップデートする」
kyo-dskyo-ds

NumPy mean の axis 指定に関するメモ

  • axis=0：縦方向に平均（各列の平均を取る）
  • axis=1：横方向に平均（各行の平均を取る）

axis は「どの方向に沿って処理するか」を指定する。
そして「指定した方向が潰れる」＝その次元がなくなる、という理解でOK。

例：2次元配列に対する mean

import numpy as np

a = np.array([[1, 2, 3],
              [4, 5, 6]])

np.mean(a, axis=0)

縦方向（行方向）に計算 → 各列の平均

np.mean(a, axis=0)
# 出力: array([2.5, 3.5, 4.5])

計算内容:

  • 1列目: (1 + 4) / 2 = 2.5
  • 2列目: (2 + 5) / 2 = 3.5
  • 3列目: (3 + 6) / 2 = 4.5

np.mean(a, axis=1)

横方向（列方向）に計算 → 各行の平均

np.mean(a, axis=1)
# 出力: array([2.0, 5.0])

計算内容:

  • 1行目: (1 + 2 + 3) / 3 = 2.0
  • 2行目: (4 + 5 + 6) / 3 = 5.0
kyo-dskyo-ds

ロジスティック回帰の実装：勾配計算の完全理解

1. 全体アーキテクチャ

ロジスティック回帰は以下の構成で成り立っています：

  • 線形変換：
z = w^T x + b
  • シグモイド関数：
\hat{y} = \frac{1}{1 + e^{-z}}
  • 損失関数（負の対数尤度）：
L = -\sum \left[ y \log \hat{y} + (1 - y) \log(1 - \hat{y}) \right]
  • 勾配計算：パラメータ w, b の更新に使います。

2. 順伝播の次元構造

変数 形状 説明
x (N, D) 入力データ（N: データ数, D: 特徴量数）
w (D,) 重みベクトル
b スカラー バイアス
z (N,) 線形変換の出力
ŷ (N,) シグモイドを通した確率出力

3. 逆伝播の流れ

(1) 損失に対する出力の勾配：

dy = - (y_true / y_pred) + (1 - y_true) / (1 - y_pred)  # shape: (N,)

(2) シグモイドの勾配：

\frac{d\hat{y}}{dz} = \hat{y} (1 - \hat{y}) 
dz = dy * y_pred * (1 - y_pred)  # shape: (N,)

(3) パラメータ勾配：

dw = np.sum(dz[:, None] * x, axis=0)  # shape: (D,)
db = np.sum(dz)  # shape: ()

4. 次元が登場するポイント

  • dy や dz はスカラー的な誤差の流れ（shape: N）
  • 特徴量に依存した重みの勾配は dw で初めて形状 (D,) を持つ
  • 線形変換 z = w^T x が特徴量ごとに寄与するため

5. 実装コード（NumPy）

import numpy as np

class Sigmoid:
    def forward(self, x, w, b):
        self.x = x
        z = x @ w + b
        self.y_pred = 1 / (1 + np.exp(-z))
        return self.y_pred

    def backward(self, dy):
        dz = dy * self.y_pred * (1 - self.y_pred)
        dw = np.sum(dz[:, None] * self.x, axis=0)
        db = np.sum(dz)
        return dw, db

class NegativeLogLikelihood:
    def forward(self, y_pred, y_true):
        self.y_pred = y_pred
        self.y_true = y_true
        loss = -np.sum(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
        return loss

    def backward(self):
        return - (self.y_true / self.y_pred) + (1 - self.y_true) / (1 - self.y_pred)

def train(X, y, epochs=100, lr=0.01):
    D = X.shape[1]
    w = np.zeros(D)
    b = 0.0
    sigmoid = Sigmoid()
    loss_fn = NegativeLogLikelihood()

    for epoch in range(epochs):
        y_pred = sigmoid.forward(X, w, b)
        loss = loss_fn.forward(y_pred, y)
        dy = loss_fn.backward()
        dw, db = sigmoid.backward(dy)
        w -= lr * dw
        b -= lr * db
        if epoch % 10 == 0:
            print(f"Epoch {epoch}: Loss = {loss:.4f}")

    return w, b

6. 数式的根拠

  • 損失関数の定義：
L = \sum_{i=1}^{N} L_i
  • 勾配の線形性：
\frac{\partial L}{\partial w} = \sum_{i=1}^{N} \frac{\partial L_i}{\partial w}

7. Tips

✅ 学習率調整

lr = 0.01

✅ ミニバッチ化

for i in range(0, len(X), batch_size):
    X_batch = X[i:i+batch_size]
    y_batch = y[i:i+batch_size]

✅ 数値勾配で検証

def numerical_grad(f, x, eps=1e-4):
    grad = np.zeros_like(x)
    for i in range(x.size):
        x_plus = x.copy()
        x_minus = x.copy()
        x_plus.flat[i] += eps
        x_minus.flat[i] -= eps
        grad.flat[i] = (f(x_plus) - f(x_minus)) / (2 * eps)
    return grad
kyo-dskyo-ds

🧠 SVM（サポートベクターマシン）とカーネルトリックとは？

✅ SVMとは？

SVM（Support Vector Machine）は、分類や回帰に使われる教師あり学習の手法です。特に、2クラス分類問題でよく使われます。

🎯 SVMの目的

クラス間のマージン（余白）を最大化する境界線（超平面）を見つけること。

データ点の中で、**マージンに最も近い点（=サポートベクター）**に注目して、これらの点からマージンを決定します。

✏️ 数式的な定義（線形SVM）

2クラス分類問題を考えます。各データ (x_i, y_i) に対して：

  • x_i は特徴量ベクトル（\in \mathbb{R}^n）
  • y_i はラベル（+1 または -1）

超平面：

w \cdot x + b = 0

分類のルール：

\text{sign}(w \cdot x + b)

マージン最大化のための最適化問題：

\min_{w, b} \frac{1}{2} \|w\|^2 \\ \text{subject to } y_i(w \cdot x_i + b) \geq 1 \quad \forall i

🧱 ソフトマージン（誤分類を許容）

現実のデータは完全に分離できないことが多いです。そこで「ソフトマージンSVM」では、スラック変数 \xi_i を導入して、以下のようにします：

\min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^n \xi_i \\ \text{subject to } y_i(w \cdot x_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0
  • C は正則化パラメータ（誤分類をどれだけ許すかのトレードオフ）

🌐 カーネルトリックとは？

線形では分離できないデータもあります。

そこで「高次元空間に写像して線形分離できるようにする」のがカーネルトリック。

たとえば、以下のような特徴空間への変換を考える：

\phi: \mathbb{R}^n \rightarrow \mathbb{R}^m \quad (m > n)

でも…

高次元空間で計算するのはコストが高い！

✨ カーネルトリックのアイデア

内積だけで計算できるなら、写像せずに直接カーネル関数 K(x, x') を使えばいい！

K(x, x') = \phi(x) \cdot \phi(x')

🔧 よく使われるカーネル関数

カーネル名 数式 特徴
線形カーネル K(x, x') = x \cdot x' 高速、単純
多項式カーネル K(x, x') = (x \cdot x' + c)^d 非線形性を導入
RBFカーネル（ガウシアン） K(x, x') = \exp(-\gamma |x - x'|^2) 非線形、局所性重視

💡 カーネルトリックの利点

  • 高次元空間での明示的な計算を回避できる
  • 非線形なパターンを学習できる
  • 理論的に強力（凸最適化問題になる）

📌 まとめ

  • SVMはマージン最大化を目指す分類器
  • 線形SVMは単純だが限界もある
  • カーネルトリックを使えば、非線形分離も可能になる！

📚 参考

kyo-dskyo-ds

RNNの出力層とBPTTの仕組みまとめ

1. RNNの基本構造

  • 入力 x_t と前の隠れ状態 h_{t-1} を受け取って、新しい隠れ状態 h_t を計算：
h_t = f(W_x x_t + W_h h_{t-1} + b_h)

ここで：

  • W_x：入力用の重み
  • W_h：再帰部分の重み
  • b_h：バイアス
  • f：活性化関数（例：tanh や ReLU）

2. 出力層の役割

RNNが作った隠れ状態 h_t を、そのままでは使えないので 出力層 でタスクに合わせて変換します：

z_t = W_o h_t + b_o
  • W_o：出力層の重み行列
  • b_o：出力層のバイアス

なぜ W_o が必要か？

  • 隠れ状態と出力空間の次元が異なるため、多様なタスクに柔軟に対応する必要がある
  • 例：隠れ状態 100 次元 → 語彙数 30,000 の確率分布などへ

3. 出力形式の違い（分類 vs 回帰）

二値分類

  • 出力：1 次元
  • 活性化：Sigmoid
\hat{y}_t = \sigma(W_o h_t + b_o)
  • 損失：バイナリクロスエントロピー

多クラス分類

  • 出力：複数クラス（例：語彙サイズ）
  • 活性化：Softmax
\hat{y}_t^{(i)} = \frac{\exp(z_t^{(i)})}{\sum_j \exp(z_t^{(j)})}
  • 損失：クロスエントロピー

回帰

  • 出力：連続値（1 次元またはベクトル）
  • 活性化：なし（恒等写像）
\hat{y}_t = W_o h_t + b_o
  • 損失：MSE（平均二乗誤差）や MAE（平均絶対誤差）

4. BPTT（Backpropagation Through Time）の流れ

順伝播

  1. 各時刻で h_t を計算
  2. 出力 z_t を生成し、Softmax／Sigmoid／恒等写像に通して \hat{y}_t を得る
  3. 損失 L を計算

逆伝播（BPTT）

  1. 損失 L から出力層の勾配を計算
    • 更新：dW_o, db_o
    • 誤差を h_t に逆流させる
  2. 各時刻の RNNセルに勾配を伝播
  3. 時間方向に巻き戻しながら累積してパラメータを更新

5. まとめ

  • W_o は隠れ状態から出力空間への重要な変換
  • 活性化関数はタスクに応じて使い分ける
    • 多クラス → Softmax
    • 二値 → Sigmoid
    • 回帰 → 恒等写像
  • BPTT は時間を巻き戻しながら逆伝播してパラメータを調整する手法