Pythonで学ぶはじめての聴覚フィルタ（やさしい？解説）

1. はじめに

サイバーエージェント AI Labのやまかつ(@kyama0321)です。AI Labでは、AudioチームのResearch Scientistとして、ヒトの聴覚特性に基づく音声情報処理の研究をしています。

本記事は、日本音響学会 学生・若手フォーラム Advent Calendar 2023の22日目の記事になります。引越しが無事に終わった（？）ので、やっと書く気になりました。

タイトルから既におわかりのように、　本記事は日本音響学会誌2010年66巻10号に掲載された"はじめての聴覚フィルタ(やさしい解説)[1]"の導入部分を、Pythonで学べるようにしたものです。元の記事ではMATLAB/Octave版の学習ツールのみの配布となっておりますが、私が趣味で作成した　Python版ガンマチャープフィルタ (GammachirPy;がんまちゃーぴー)[2]　をもとに Jupyter Notebook上で動作できるようにしています。そのため、ご自身の環境構築は不要で、Google Colabへのリンクを押すだけで、ブラウザ上で気軽に学習できるのが特徴です。

本記事は、無料で閲覧可能な "はじめての聴覚フィルタ(やさしい解説) [1]" の2.2節の内容をスクリプトベースで紹介しています。聴覚フィルタの基本概念を学ぶためにも、文献[1]を並行して読み進めることをおすすめします。

2.GammachirPyについて

GammachirPy[2]は、聴覚フィルタの代表例である「ガンマチャープフィルタ[3]」および「動的圧縮型ガンマチャープフィルタバンク[4]」をPython環境で動作できるようにした個人的なopen-source software(OSS)プロジェクトです。

動的圧縮型ガンマチャープフィルタバンク自体は現在も積極的に改良が進められており、その更新にも随時対応できるように、オリジナル版（MATLAB）の体裁をできるだけ保ったまま、Pythonコードに翻訳しているのが特徴です。また、Pythonで実装することによって、コアとなるパッケージをそのまま利用して、Google　Colabのようなオンライン環境でも動作することができるようになりました。

ちなみに、GammachirPyの読み方を"がんまちゃーぴー"にしたのは、当時流行っていたあの漫画の影響です🐙

3. さっそく動かしてみよう

3.1.セットアップ

1. 以下のリンクから、Google　Colab上の demo_gammachirp_notebook.ipynb を開いてください。
   

2. For Google Colaboratory Users のコメントアウトを取り除いてください。
   

3. For Google Colaboratory Users と For All Users のセクションを実行してください。以下のように表示されればセットアップ完了です。
   

以降では、Notebookに記載されている順に、解説を進めていきます。

3.2. 周波数応答（利得特性）

3.2.1. 入力の音圧レベルが一定の場合

まずはじめにガンマチャープフィルタのパラメータを設定していきます。このパラメータを聴取実験データを基に調整することで、個々人の聴覚特性に合わせる（フィッティングする）こともできます。

今回は入力信号の音圧レベルのパラメータ ps を一定にして、異なるピーク周波数（中心周波数）の聴覚フィルタの周波数応答（利得特性）を見ていきます。

# Parameter values from Patterson+ (2003)
n = 4       
b1 = 1.81   
c1 = -2.96  
b2 = 2.17   
c2 = 2.20   
frat0 = 0.466
frat1 = 0.0109

n_rsl = 2**12
fs = 44100

ps = 50 # input level (dB)
frat = frat0 + frat1 * ps

今回は、250　Hz、500　Hz、1000　Hz、2000　Hz、4000　Hz、8000 Hzに聴覚フィルタのゲインがピーク（0 dB）になるように設定します。最後の行は、周波数のスケールを線形スケールから、等価矩形帯域幅 (equivalent rectangular bandwidth; ERB) という聴覚的なスケールに置き換えています。ERBについては3.3節で後ほど説明します。

# peak frequency of each filter channel
fp_list = np.array([250, 500, 1000, 2000, 4000, 8000])
fp_xtick = np.array([100, 250, 500, 1000, 2000, 4000, 8000, 16000])
erb_n_xtick, _ = utils.freq2erb(fp_xtick)

上記のパラメータをもとに、gammachirp filterbankの周波数応答を計算して、周波数が低い順にプロットしていきます。スクリプト中のfratが入力の音圧レベルに依存するパラメータです。

fig, ax = plt.subplots()

for ifp, fp in enumerate(fp_list):
    # calculate frequency renponse
    fr1, _ = gcfb.fp2_to_fr1(n, b1, c1, b2, c2, frat, fp)
    cgc_resp = gcfb.cmprs_gc_frsp(fr1, fs, n, b1, c1, frat, b2, c2, n_rsl)
    cgc_frsp = cgc_resp.cgc_frsp
    
    # convert level and frequency scale to plot
    cgc_frsp_db = 20 * np.log10(cgc_frsp/np.max(cgc_frsp))
    freq = np.array(cgc_resp.freq)
    erb_num, _ = utils.freq2erb(freq)

    # plot frequency renponse of each filter
    plt.plot(erb_num[0, :], cgc_frsp_db[0, :], color=cmap(ifp))
    ax.set_xlim([erb_n_xtick[0], erb_n_xtick[-1]])
    ax.set_ylim([-70, 5])
    ax.set_xticks(erb_n_xtick)
    ax.set_xticklabels(fp_xtick)
    ax.set_xlabel("frequency (Hz)")
    ax.set_ylabel("filter gain (dB)")
    plt.title("frequency response")

plt.grid()

plt.show()

上記のスクリプトを実行して得られたのが以下の周波数応答（利得特性）です。横軸が周波数(Hz)、縦軸がフィルタの利得(dB)です。聴覚フィルタの一つ目の特徴として、フィルタ形状が周波数方向に非対称であることが挙げられます。

3.2.2. 入力の音圧レベルが変化する場合

ヒトの聴覚フィルタの二つ目の特徴として、入力音圧レベルに依存して周波数応答が変化することが挙げられます。つまり、聴覚フィルタは非線形なフィルタであると言えます。本項では、入力の音圧レベルが増加することで、どのように聴覚フィルタの周波数特性が変化するかをみていきましょう。

入力音圧レベルのパラメータ ps を変化させるために、以下のリストのようにパラメータを変化させます。また、プロットをわかりやすくするために、線の種類のリストも作成しておきます。

ps_list = [50, 70, 90] # dB
plt_line_list = ['-', '--', ':']

2.2.1項のスクリプトを、音圧レベルの変化も反映できるように拡張します。なお、ここでは一番小さい入力音圧レベル(ps=50)のときの利得のピークが0 dBになるように、正規化を行なっています。

fig, ax = plt.subplots()

max_cgc_frsp = np.zeros(len(fp_list))

for ips, ps in enumerate(ps_list): 
    # change frat with ps (input level)
    frat = frat0 + frat1 * ps

    for ifp, fp in enumerate(fp_list):
        # calculate frequency renponse
        fr1, _ = gcfb.fp2_to_fr1(n, b1, c1, b2, c2, frat, fp)
        cgc_resp = gcfb.cmprs_gc_frsp(fr1, fs, n, b1, c1, frat, b2, c2, n_rsl)
        cgc_frsp = cgc_resp.cgc_frsp

        if ips == 0:
            # save peak level of each filter
            max_cgc_frsp[ifp] = np.max(cgc_frsp)
        
        # convert level and frequency scale to plot
        cgc_frsp_db = 20 * np.log10(cgc_frsp/max_cgc_frsp[ifp])
        freq = np.array(cgc_resp.freq)
        erb_num, _ = utils.freq2erb(freq)

        # plot frequency renponse of each filter
        plt.plot(erb_num[0, :], cgc_frsp_db[0, :], plt_line_list[ips], color=cmap(ifp))
        ax.set_xlim([erb_n_xtick[0], erb_n_xtick[-1]])
        ax.set_ylim([-70, 5])
        ax.set_xticks(erb_n_xtick)
        ax.set_xticklabels(fp_xtick)
        ax.set_xlabel("frequency (Hz)")
        ax.set_ylabel("filter gain (dB)")
        plt.title("frequency response: different input levels")

plt.grid()

plt.show()

上のスクリプトを実行した結果が以下のプロットです。横軸が周波数(Hz)、縦軸がフィルタの利得(dB)です。色が同じピーク周波数、線種が同じ入力音圧レベルの聴覚フィルタになっています。

入力音圧を変更することによって、聴覚フィルタの周波数応答も変化していることがわかります。詳細については、3.4節で説明します。

3.3 中心周波数と等価矩形帯域幅(ERB)の関係

3.2.1項や3.2.2項の結果を見ると、聴覚フィルタの帯域幅は広域になるにつれて広がっていく（分解能が低くなる）ということがわかります。この中心周波数（ピーク周波数）と帯域幅のおおよその関係は、等価矩形帯域幅 (equivalent rectangular bandwidth; ERB)　として、健聴者のデータをもとに定式化されています。

以下のスクリプトで、その中心周波数とERBの関係をプロットしてみましょう。

# convert linear frequency to ERB_N scale
freq = np.arange(100, 12000+1, 100)
_, erb_n = utils.freq2erb(freq)

# plot in log scale
fig, ax = plt.subplots(figsize=(5,5))
plt.loglog(freq, erb_n)
ax.set_xlim([50, 15000])
ax.set_ylim([20, 2500])
plt.grid(which='both')
ax.set_xlabel("center frequency (Hz)")
ax.set_ylabel("equivalent rectanglar bandwidth (Hz)")
plt.title("center frequency vs. ERB width")

plt.show()

プロットされた結果をみると、約500 Hz以上では中心周波数とERBがほぼ比例関係になっていることがわかります。2.2.1項や2.2.2項のプロットにおいて、異なる帯域幅でありながら、どれも等間隔のフィルタに見えるのは、このERBの関係式をもとに横軸のスケールを変更しているからです。

ほかにも、似たようなスケール変換として、メルフィルタバンクで用いられているmel尺度やBark尺度が挙げられます。

3.4　音圧依存性と入出力特性

前節では、異なる中心周波数での聴覚フィルタ群の応答を俯瞰的にみましたが、本節では特定の中心周波数のフィルタに対する応答を見ていきます。

中心周波数のパラメータ fp を2000 Hzに固定して、入力音圧レベルのパラメータ ps を30 dBから90 dBまで10 dB刻みで増加していきます。また、プロットをわかりやすくするために、マーカーの種類のリストも作成しておきます。

marker = ['o', 'x', 'd', '*', '^', 'p', 's']

fp = 2000 # peak frequency (Hz)
ps_list = [30, 40, 50, 60, 70, 80, 90] # input level (dB)

今回も同様に一番小さい入力音圧レベル(ps=30)のときの利得の最大値が0 dBになるように、正規化を行なっています。

fig, ax = plt.subplots(figsize=(5,5))

cgc_frs_db_max = np.array([])
for ips, ps in enumerate(ps_list):
    # input level changes dcGC parameters
    frat = frat0 + frat1 * ps

    # calculate frequency renponse
    fr1, _ = gcfb.fp2_to_fr1(n, b1, c1, b2, c2, frat, fp) 
    cgc_resp = gcfb.cmprs_gc_frsp(fr1, fs, n, b1, c1, frat, b2, c2, n_rsl)
    cgc_frsp = cgc_resp.cgc_frsp

    # reference: peak level at the smallest input level (30 dB)
    if ips == 0:
        cgc_frsp_ref = np.max(cgc_frsp)

    # calculate relative frequency response 
    cgc_frsp_db = 20 * np.log10(cgc_frsp/np.max(cgc_frsp_ref))
    freq = np.array(cgc_resp.freq)
    cgc_frs_db_max = np.append(cgc_frs_db_max, np.max(cgc_frsp_db))

    # plot
    plt.plot(freq[0, :], cgc_frsp_db[0, :], color=cmap(ips))
    plt.plot(fp, cgc_frs_db_max[ips], marker[ips], color=cmap(ips), markersize=8)
    ax.set_xlim([0, 4000])
    ax.set_ylim([-70, 5])
    ax.set_xticks([0, 1000, 2000, 3000, 4000])
    ax.set_xlabel('frequency (Hz)')
    ax.set_ylabel('filter gain (dB)')
    plt.grid()
    plt.text(fp*1.05, cgc_frs_db_max[ips], f"{ps}")

plt.text(fp*1.15, 1.0, 'input level (dB)')
plt.title('frequency response')

plt.show()

上記のスクリプトを実行して得られたプロットを以下に示します。横軸が周波数(Hz)、縦軸がフィルタの利得(dB)です。色が入力音圧レベル、マーカーがそれぞれの応答における利得の最大値(dB)を示しています。

入力音圧が上昇するとともに利得が現象し、フィルタの帯域幅も広域化（利得の最大値が大きく下がっているのに、周辺の利得はさほど下がっていない）していることがわかります。

この利得の最大値の変化を入出力応答の関係（入出力関数）としてプロットしてみましょう。なお、以下のスクリプトでは、90 dBの入力音圧に対して出力が90 dBになるように補正を行なっています。

fig, ax = plt.subplots(figsize=(5,5))

# adjust output level to 90 dB when the input level is 90 dB
output_level = cgc_frs_db_max + ps_list + 33

# plot I/O function with a "linear" I/O function
plt.plot(ps_list, output_level, 'k', ps_list, ps_list, ':k')

# plot markers at each corrspond I/O level 
for cnt in range(len(output_level)):
    plt.plot(ps_list[cnt], output_level[cnt], marker[cnt], \
        color=cmap(cnt), clip_on = False, markersize=8)

ax.set_xlim([30, 90])
ax.set_ylim([30, 90])
ax.set_xlabel("input level (dB)")
ax.set_ylabel("output level (dB)")
plt.title("I/O function")
plt.grid()

plt.show()

上記のスクリプトを実行して得られるのが以下の入出力応答です。横軸は入力音圧レベル（dB）、縦軸は聴覚フィルタの最大利得(dB)です。各マーカーは、一つ前の図における聴覚フィルタの最大利得に対応しています。点線は入出力特性が1:1の増加率で線形な場合を示しています。

点線と比較すると、30 dB付近の低い音圧レベル（左側）では利得が30 dB以上増加しているのに対し、90 dB付近では利得がほとんど無くなっていることがわかります。つまり、聴覚フィルタは小さい音ほど利得を増大させ、大きい音ほど利得を減少させていると言えます。これを、聴覚心理の立場では 圧縮特性(compression) と読んでいます。

皆さんが小さい音を耳を澄まして聞けたり、ライブ会場のような場所で大きい音で音楽を聞くことができるのは、この圧縮特性によって聴覚が幅広いダイナミックレンジを担保できているからだと考えることができます。

4.音響分析ツールとして使ってみよう

聴覚フィルタバンクを使用することで、聴覚特性に基づいた音響分析を行うことができます。ここでは、ガンマチャープフィルタで時間応答が得られるように拡張された動的圧縮型ガンマチャープフィルタバンク[3]を用いて音声を分析してみたいと思います。

4.1.セットアップ

1. 以下のGoogle　Colabリンクからdemo_gcfb_v211_speech.ipynbを開きます。
   

2. For Google Colaboratory Users のコメントアウトを取り除いてください。
   

3. For Google Colaboratory Users と For All Users のセクションを実行してください。以下のように表示されればセットアップ完了です。
   

4.2 パラメータの設定

動的圧縮型ガンマチャープフィルタのパラメータを定義します。今回は100 Hzから6000 Hzの間にピークを持つ100チャンネル分のガンマチャープフィルタを等間隔に配置していきます。また、等ラウドネス曲線（equal loudness contour）[5]に基づいて周波数特性を補正しています。最後のパラメータは圧縮特性を時変/時不変にするパラメータで、基本的に 'dynamic' を指定します。

class GCparamDefault:
        fs = 48000 # sampling frequency
        num_ch = 100 # number of channels
        f_range = np.array([100, 6000]) # range of center frequencies
        # out_mid_crct = "No" # outer & middle ear correlations
        out_mid_crct = 'ELC' # equal loudness contour (ELC)
        ctrl = 'dynamic' # time-varying
        # ctrl = 'static' # not time-varying (fixed)

4.3 音声データの読み込み

適当に録音した誰かの声を読み込みます。一体、どんなテンションで録音したんだろうでしょうか…

# stiuli : a sample speech sound
file_name = 'snd_gammachirpy.wav'
path_dir = './sample/'
path_file = path_dir + file_name

# read sample speech
snd, fs = utils.audioread(path_file)
t_snd = len(snd)/fs
t = np.arange(0, len(snd), 1)/fs
print(f"Duration of sound = {t_snd*1000} (ms)")

波形

# Plot the input signal
fig, ax = plt.subplots()
ax.plot(t, snd)
ax.set_title("Input: speech sound")
ax.set_xlabel("time (s)")
ax.set_ylabel("amplitude")
plt.grid()

plt.show()

4.4 音声データの分析

入力音圧レベルを指定して100チャンネル分の出力（波形）を取得します。ここでは、入力音圧レベルdpsplを指定した後に、 "Meddisの内有毛細胞レベル[6]" という音圧レベル(RMS値が1のとき、音圧レベルが30 dB)に校正しています。

# sound pressure level (SPL)
dbspl = 40

# Level equalization
snd_eq, _ = utils.eqlz2meddis_hc_level(snd, dbspl)

# GCFB
gc_param = GCparamDefault()
cgc_out, pgc_out, _, _ = gcfb.gcfb_v211(snd_eq, gc_param)

上記のスクリプトを実行すると以下のように表示されます。このバージョン(v211)の動的圧縮型ガンマチャープフィルタバンクは1サンプルづつ計算を行うので、非常に時間がかかってしまうことにだけご注意ください。

*** Outer/Middle Ear correction (minimum phase) : ELC ***
*** OutMidCrctFilt: Generating ELC FIR minimum phase filter ***
*** Gammachirp Calculation ***
--- Channel-by-channel processing ---
Passive-Gammachirp & Level estimation filter ch #1 / #100.   elapsed time = 0.0 (sec)
Passive-Gammachirp & Level estimation filter ch #20 / #100.   elapsed time = 0.3 (sec)
Passive-Gammachirp & Level estimation filter ch #40 / #100.   elapsed time = 0.5 (sec)
Passive-Gammachirp & Level estimation filter ch #60 / #100.   elapsed time = 0.7 (sec)
Passive-Gammachirp & Level estimation filter ch #80 / #100.   elapsed time = 0.9 (sec)
Passive-Gammachirp & Level estimation filter ch #100 / #100.   elapsed time = 1.2 (sec)
--- Sample-by-sample processing ---
ACFilterBank: Initialization of acf_status
Dynamic Compressive-Gammachirp: Time 0.0 (ms) / 1343.9 (ms). elapsed time = 0.0 (sec)
Dynamic Compressive-Gammachirp: Time 134.4 (ms) / 1343.9 (ms). elapsed time = 8.6 (sec)
Dynamic Compressive-Gammachirp: Time 268.7 (ms) / 1343.9 (ms). elapsed time = 17.4 (sec)
Dynamic Compressive-Gammachirp: Time 403.1 (ms) / 1343.9 (ms). elapsed time = 24.9 (sec)
Dynamic Compressive-Gammachirp: Time 537.5 (ms) / 1343.9 (ms). elapsed time = 33.7 (sec)
Dynamic Compressive-Gammachirp: Time 671.9 (ms) / 1343.9 (ms). elapsed time = 41.1 (sec)
Dynamic Compressive-Gammachirp: Time 806.2 (ms) / 1343.9 (ms). elapsed time = 49.8 (sec)
Dynamic Compressive-Gammachirp: Time 940.6 (ms) / 1343.9 (ms). elapsed time = 58.5 (sec)
Dynamic Compressive-Gammachirp: Time 1075.0 (ms) / 1343.9 (ms). elapsed time = 65.9 (sec)
Dynamic Compressive-Gammachirp: Time 1209.4 (ms) / 1343.9 (ms). elapsed time = 74.6 (sec)
Dynamic Compressive-Gammachirp: Time 1343.7 (ms) / 1343.9 (ms). elapsed time = 81.9 (sec)

出力結果をプロットします。ここでは、可視化のしやすさを優先するために、スムージングと補正値（利得）を入れています。

# Caluculation of smoothed spectrogram from GCFB
gcfb_param = GCparamDefault()
gcfb_param.fs = fs # using default. See inside cal_smooth_spec for parameters
aud_spec, _ = gcfb.cal_smooth_spec(np.maximum(cgc_out, 0), gcfb_param)

# Plot
if gc_param.ctrl == 'dynamic':
    amp_img = (64*1.2)/49
else:
    amp_img = (64*1.2)/166

fig, ax = plt.subplots()
plt.imshow(amp_img*aud_spec, extent=[min(t), max(t), 0, 100], \
            aspect='auto', origin='lower', cmap='jet')
ax.set_title(f"GCFB control = {gc_param.ctrl}; Signal Level = {dbspl} dB SPL")
ax.set_yticks([0, 20, 40, 60, 80, 100])
ax.set_xlabel("time (s)")
ax.set_ylabel("channel")

plt.show()

上記のスクリプトを実行すると、以下の "聴覚的な" スペクトログラムが得られます。横軸は時間（s)、縦軸はガンマチャープフィルタのチャンネルになります。チャンネル番号が小さいものは低域、大きいものは高域の聴覚フィルタです。

音圧レベル：40 dB

この入力音圧レベルが変わるとどのように出力が変化するか、同様の方法で出力してみましょう。

音圧レベル：60 dB

音圧レベル：80 dB

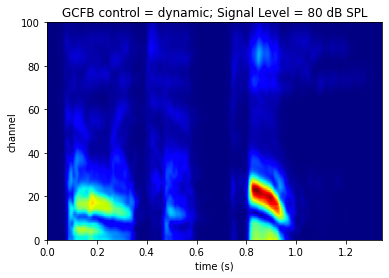
音圧が上昇することで聴覚フィルタの形状や利得特性が変化し、分析結果にも違いが現れるようになりました。このことから、聴覚フィルタは入力音圧に依存した時変で非線形なフィルタであることがわかります。また、このような出力（特徴量）を使用することで、聴覚特性に基づく音響分析を行うことが可能になります。

5.おわりに

本記事では、Pythonスクリプトを用いて聴覚フィルタについて解説しました。なお、今回は紹介できませんでしたが、demo_gammachirp.ipynbの後半には、ガンマチャープフィルタの構成（本記事のトップ画像）や、マスカ音に対する応答、線形なガンマトーンフィルタとの比較についても、紹介しています（書籍[7,8]のプロットを再現できるようになっています）。

今回のデモスクリプトでは比較的古いバージョン(v211)の動的圧縮型ガンマチャープフィルタバンクを使用しています。オリジナル（MATLAB）の最新版では、フレーム処理による高速化や難聴者特性の追加などが行われており、GammachirPyでも公開の準備を進めているところです。

[2024/05/14追記]　GammachirPyの最新版（v234）を公開しました🎉

聴覚フィルタに興味を持った方は、より専門的な書籍[7,8,9]にも挑戦してみてください！また、実装にも興味があれば、GammachirPyプロジェクトに協力していただけると幸いです！

参考文献

[1] 入野, "はじめての聴覚フィルタ(やさしい解説)," 日本音響学会誌, Vol.66, No.10, pp.506-512, 2010.
[2] kyama0321/GammachirPy(GitHub)
[3] Roy D. Patterson, M Unoki, and T. Irino "Extending the domain of center frequencies for the compressive gammachirp auditory filter," J. Acoust. Soc. Am., Vol.114, No.3, pp.1529-1542, 2003.
[4] T. Irino and R. D. Patterson, "A dynamic compressive gammachirp auditory filterbank" IEEE Trans. Audio, Speech, and Language Process., Vol.14, No.6, pp.2222-2232, 2006.
[5] 鈴木 陽一, 等ラウドネスレベル曲線の国際標準化, 日本音響学会誌, Vo.78, No.2, p. 88-91, 2022
[6] Ray Meddis, "Simulation of mechanical to neural transduction in the auditory receptor," J. Acoust. Soc. Am., Vol.79, No.3, pp.702–711.
[7]日本音響学会 編, "聴覚モデル," 音響サイエンスシリーズ, Vol.3, コロナ社, pp.101-128, 2011.
[8]日本音響学会 編, "聴覚," 音響学講座, Vol.5, コロナ社, pp.25-48, 2011.
[9]リチャード・F・ライオン, "ヒトの耳・機械の耳 聴覚のモデル化から機械学習まで," 東京電機大学出版局, 2021.