VOS: Learning What You Don't Know by Virtual Outlier Synthesis の解説・実装
はじめに
こんにちは、わっしーです。
画像・自然言語・音声に関する機械学習の研究開発やMLOpsを行っています。もし、機械学習に関して、ご相談があれば、@kwashizzzのアカウントまでDMしてください!
これまでの、機械学習記事のまとめです。
本記事では、Out-of-Distribution (OOD)検出の新しい手法であるVOS: Learning What You Don't Know by Virtual Outlier Synthesisに関して紹介します。OOD検出とは、例えば、犬と猫の分類モデルに対して人の画像を入れた場合、学習したクラス以外と認識するタスクのことです。
今までの手法は、実際のクラス外のデータが必要で、データ作成にコストがかかったり、そもそも取得不可能場合もありました。しかし、VOS(Virtual Outlier Synthesis)では、クラス外のデータは必要ありません。そのため、かなり実用的な手法だと思い、記事にしました。
また、本記事では、犬猫のクラス分類を例に、実際の実装も紹介します。
VOSについて
手法の概要は、論文中Fig.2の以下の図です。
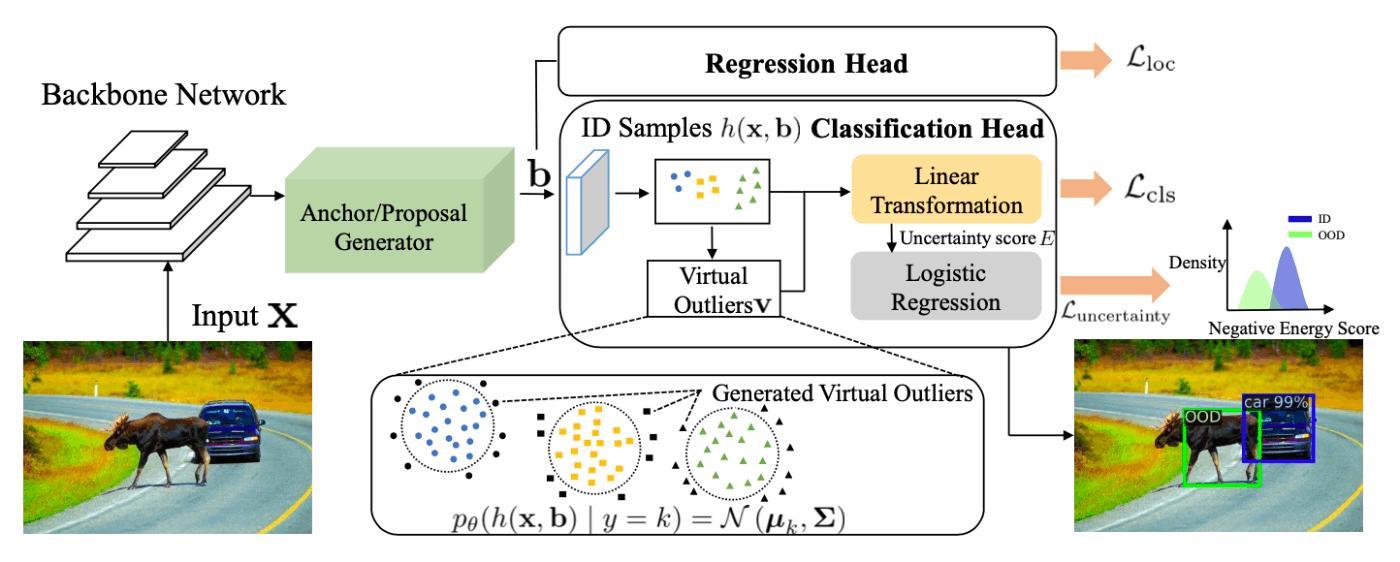
物体検出の例ですが、牛が学習データに含まれておらず、一般的な物体検出モデルでは、通行人と誤って検出されてしまいましたが、VOSによりOODと検出されています。基本的には、一般的な物体検出と同じですが、VOSは以下の特徴があります。
-
VOSは、In-Distribution(ID)データ(学習データ)とOODデータ(外れ値データ)を用いて、外れ値かどうか2値分類を行うモデルを学習しています。ここで、外れ値のデータとして、モデルの最終FC層の一つ前の層(Classification Head部分)から、仮想的な外れ値(Virtual Outliers)を合成しています。GANで外れ値画像を合成することも考えられますが、より低次元の特徴空間で合成することで、効率良いOOD検出の学習が可能になっています。
-
論文では、分類などのタスクに加えて、OOD検出タスクも同時に学習する損失関数が提案されています。
-
画像分類、物体検出どちらでも使用可能です。今までのアプローチと異なり、VOSでは、物体検出におけるOODにも取り組んでいます。物体検出でOODを行うことで、多数の物体から構成された画像でも部分的なOOD検出を可能にしています。
-
VOSは画像検出・物体検出のモデルの分類部分を一部拡張するだけで使用でき、特徴抽出部分を修正する必要がないため、事前学習済みのモデルが使用できます。
外れ値の合成手法
一般的な学習方法では、In-Distribution(ID)データのみで最適化されるため、下図中央(論文中Fig.1 (b))のように、IDがガウス分布から形成されるが、IDから離れた部分を過信するような結果となることが多々あります。理想的には、下図右のように、IDデータに対してスコアが高く、それ以外のOOD領域では、スコアが低くなるようにして、OOD検出の決定境界を学習したいです。そこで、仮想外れ値の合成が必要となります。

仮想外れ値の合成では、物体インスタンスの特徴表現が、クラス条件付き多変量ガウス分布を形成していると仮定しています。ガウス分布の平均と分散は、特徴表現(ニューラルネットワークの最後から2番目の層)のサンプルから計算できます。
実装では、クラス条件付き待ち行列
この多変量ガウス分布の尤度が低い部分から、サンプリングした値が仮想外れ値と考えられます。そこで、以下の式のように、閾値(
このサンプリングされるものは、ニューラルネットワークの最後から2番目の層に一致する特徴表現です。そのため、最終fc層の重み
次に、上記の方法で仮想的な外れ値を合成できるとし、どのような損失で学習するのか解説します。
VOSの損失
論文では、IDに対しては低いOODスコアを、合成された外れ値に対しては高いOODスコアを生成するように、モデルを正則化しながら学習する損失を提案しています。以下、色々式がありますが、合成した外れ値も入れて、学習データと合成データを分離する境界を効率的に学習したいだけだと思います。
物体検出バージョンは、画像分類の単純な拡張なため、簡単のため、画像分類メインで説明します。
分類のための不確かさ正則化
理想的には、データ密度
しかし、
ログ分配関数は、自由エネルギーとも呼ばれ、OOD検出のための有効な不確かさ測定であることが示されています。ラベル
VOSでは、合成された外れ値に対して正のエネルギーを持ち、IDデータに対して負のエネルギー値を持つ、エネルギー関数に基づく不確かさ損失を定義しています。
これは、密度を推定するよりもシンプルな損失ですが、0/1損失の設計は困難なため、以下の式のように、滑らかに近似したバイナリシグモイド損失に置き換えた損失をVOSでは使用しています。
今までのアプローチと比較し、上記の不確かさ損失は、ハイパーパラメータフリーで使用が容易で、かつ、OOD検出時には、シグモイド関数により、確率的スコアを生成することができます。
もし、物体検出に使用する場合は、バウンディングボックスも入力として、以下の式で表されます。
そして、VOSでは、物体検出、物体分類の損失と組み合わせ、以下の損失で最適化が行われます。
推論時
入力画像
で与えられます。簡単にいうと、出力のログ分配関数を計算し、確率に変換しています。
OOD検出のため、IDとOODを区別する閾値
以下、アルゴリズムです。

実験
実験では、以下のメトリックスで評価していました。
- FPR95 : IDサンプルの真陽性率が95%であると分類器のOODサンプルの偽陽性率
- AUROC : ROC曲線の面積
- mAP: 物体検出で良く使用される性能評価指標
個人的にFPR95に関して、理解が少し足りないてないです。
他のOODアプローチと比較して、どの指標も良かったです。また、GANなど外れ値合成手法と比較しても、高性能でした。
詳細は、論文読んでください!
実装・実験
論文に記載されているコードの分類におけるOOD検出に関して、事前学習済みモデルを使用して実験してみました。
データセットは、Kaggle Dogs vs. Cats を使用させていただきました。訓練データの1割をテストデータと見なし、単純な分類、VOSを加えた分類の両方とも正解率99%程度でした。また、OOD検出の確認のため、自前の画像に加え、このリポジトリの犬とベーグル画像の見分け辛い画像を使用させていただきました。
モデルは、事前学習済みモデルとして、timmのresnet50dを使用し、最後から2番目の層の出力を64次元と小さめに設定しました。64次元の理由は、VOSの公式実装で小さめに設定されていたためです。また、実際に、128や512と大きくして試した際、次元が大きすぎて多変量ガウス分布の仮定が満たせないためか、OODの検出が上手くいかなかったです。
実験結果
実際に学習したモデルを使用してOOD検出した際の、入力画像とスコアの例を下図に示しています。スコアは、高いとIDで、低いとOODです。論文では、0.95などを閾値として挙げていました。

(a) ~ (d)は、上手くIDと認識されています。また、テストデータに含まれているIDデータですが、(e), (f), (g)はOODとして認識されています。(e)は、顔の一部のみ、(f)は人物など複数ラベルが画像に含まれている、(g)は対象物体(猫)の領域が小さいという、データセット内では少ないパターンの画像がOODとなっています。(f)や(g)などは、VOSで提案されている物体検出も踏まえたOODを行った場合、性能が改善するかもしれません。
次は、犬とベーグルのように似た画像に関してです。(h), (i)はOODと認識され、ベーグルの(k)はIDと認識されています。このような見間違いやすい物体を分けてくれると期待しましたが、やはり、データを仮想的に作成したのみだと難しい気もします。
次に、(m) ~ (q)をOODデータを入力した場合です。スコアが低くなり、OODとして認識してくれていることがわかります。これは、すごい性能だと思います。
次に、実装の重要そうな部分を解説します。
実装
※ VOSで重要そうな部分だけ記載します。
モデルは、timmをベースにし、pytorch-lightningを用いて、学習・テストを行っています。
Resnet52dをベースにした、VOSモデルは以下です。num_out_featuresを64にしていますが、この値がOODの性能にかなり影響していました。
class ResnetVOSModule(nn.Module):
def __init__(self, num_classes):
super(ResnetVModule, self).__init__()
self.backbone = timm.create_model('resnet50d', pretrained=True, num_classes=0, global_pool="avg")
num_in_features = self.backbone.num_features
self.num_out_features = 64
self.step = nn.Sequential(
nn.BatchNorm1d(num_in_features),
nn.Linear(in_features=num_in_features, out_features=self.num_out_features, bias=False),
nn.ReLU()
)
self.fc = nn.Linear(in_features=self.num_out_features, out_features=num_classes, bias=False)
def forward(self, x):
out = self.backbone(x)
out = self.step(out)
return self.fc(out)
def forward_virtual(self, x):
out = self.backbone(x)
out = self.step(out)
return self.fc(out), out
モデルの学習部分です。ここのコードを参考にしています。
class VOSModel(pl.LightningModule):
def __init__(self, cfg: CFG):
super().__init__()
self.cfg = cfg
# 分類モデル
self.model = ResnetVOSModule(self.cfg.num_classes)
# ODのエネルギー計算式にあった重みw部分 (分類でも使用されていた。)
self.weight_energy = nn.Linear(cfg.num_classes, 1)
torch.nn.init.uniform_(self.weight_energy.weight)
# featureを溜める部分
self.number_dict = {}
for i in range(cfg.num_classes):
self.number_dict[i] = 0
self.eye_matrix = torch.eye(self.model.num_out_features, device=device)
# スコアをOOD or notで計算するロジスティク回帰
self.logistic_regression = torch.nn.Linear(1, 2)
def log_sum_exp(self, value, dim=None, keepdim=False):
"""(ログ分配関数)エネルギー計算するとこ
Numerically stable implementation of the operation
value.exp().sum(dim, keepdim).log()
"""
if dim is not None:
m, _ = torch.max(value, dim=dim, keepdim=True)
value0 = value - m
if keepdim is False:
m = m.squeeze(dim)
return m + torch.log(torch.sum(
F.relu(self.weight_energy.weight) * torch.exp(value0), dim=dim, keepdim=keepdim))
else:
m = torch.max(value)
sum_exp = torch.sum(torch.exp(value - m))
return m + torch.log(sum_exp)
def forward(self, x):
out = self.model.forward(x)
return out
def training_step(self, batch, batch_idx):
loss, acc = self._shared_train_step(batch)
self.log("train_loss", loss, logger=True)
self.log("train_acc", acc, logger=True)
return loss
def _shared_train_step(self, batch):
x, y = batch
y_hat, output = self.model.forward_virtual(x)
# 不確かさ損失の計算部分!
sum_temp = 0
for index in range(self.cfg.num_classes):
sum_temp += self.number_dict[index]
lr_reg_loss = torch.zeros(1).cuda()[0]
if sum_temp == self.cfg.num_classes * self.cfg.sample_number and self.current_epoch < self.cfg.start_epoch:
# 最初の数エポックは特徴を溜めていくのみ
# maintaining an ID data queue for each class.
target_numpy = y.cpu().data.numpy()
for index in range(len(y)):
dict_key = target_numpy[index]
self.data_dict[dict_key] = torch.cat((self.data_dict[dict_key][1:],
output[index].detach().view(1, -1)), 0)
elif sum_temp == self.cfg.num_classes * self.cfg.sample_number and self.current_epoch >= self.cfg.start_epoch:
# 特徴が溜まったら、不確かさ損失で最適化
target_numpy = y.cpu().data.numpy()
for index in range(len(y)):
dict_key = target_numpy[index]
self.data_dict[dict_key] = torch.cat((self.data_dict[dict_key][1:],
output[index].detach().view(1, -1)), 0)
# 共分散計算部分
for index in range(self.cfg.num_classes):
if index == 0:
X = self.data_dict[index] - self.data_dict[index].mean(0)
mean_embed_id = self.data_dict[index].mean(0).view(1, -1)
else:
X = torch.cat((X, self.data_dict[index] - self.data_dict[index].mean(0)), 0)
mean_embed_id = torch.cat((mean_embed_id,
self.data_dict[index].mean(0).view(1, -1)), 0)
temp_precision = torch.mm(X.t(), X) / len(X)
temp_precision += 0.0001 * self.eye_matrix # ノイズを追加
for index in range(self.cfg.num_classes):
# OODデータのサンプリング部分
# 多変量ガウス分布作成
new_dis = torch.distributions.multivariate_normal.MultivariateNormal(
mean_embed_id[index], covariance_matrix=temp_precision)
# 10000サンプリング
negative_samples = new_dis.rsample((self.cfg.sample_from,))
prob_density = new_dis.log_prob(negative_samples)
cur_samples, index_prob = torch.topk(- prob_density, self.cfg.select) #尤度が一番低いサンプル取得
if index == 0:
ood_samples = negative_samples[index_prob]
else:
ood_samples = torch.cat((ood_samples, negative_samples[index_prob]), 0)
if len(ood_samples) != 0:
# IDのエネルギー計算
energy_score_for_fg = self.log_sum_exp(y_hat, 1)
# OODのエネルギー計算
predictions_ood = self.model.fc(ood_samples)
energy_score_for_bg = self.log_sum_exp(predictions_ood, 1)
# 以下、損失計算
input_for_lr = torch.cat((energy_score_for_fg, energy_score_for_bg), -1)
labels_for_lr = torch.cat((torch.ones(len(output)).cuda(),
torch.zeros(len(ood_samples)).cuda()), -1)
criterion = torch.nn.CrossEntropyLoss()
output1 = self.logistic_regression(input_for_lr.view(-1, 1))
lr_reg_loss = criterion(output1, labels_for_lr.long())
if self.current_epoch % 5 == 0:
print(lr_reg_loss)
else:
target_numpy = y.cpu().data.numpy()
for index in range(len(y)):
dict_key = target_numpy[index]
if self.number_dict[dict_key] < self.cfg.sample_number:
self.data_dict[dict_key][self.number_dict[dict_key]] = output[index].detach()
self.number_dict[dict_key] += 1
# 全体の損失計算
loss = F.cross_entropy(y_hat, y)
loss += self.cfg.loss_weight * lr_reg_loss
# accuracy を計算する。
preds = torch.argmax(y_hat, dim=1)
acc = (y == preds).sum() / y.size(0)
return loss, acc
推論時、スコアを以下のようにして推定します。
to_np = lambda x: x.data.cpu().numpy()
# dataは画像のバッチ
output = model(data)
score = model.log_sum_exp(output, 1) # 学習にも使用した、log_sum_exp
# もし、model.weight_energyがない場合
#score = to_np(torch.logsumexp(output, dim=1))
# 以下、スコアです。これが、閾値以上だったら、ID、それ以下だったらOODとします。
score = np.exp(to_np(score)) / (1 + np.exp(to_np(score)))
まとめ
最近、話題になっていた、VOS: Learning What You Don't Know by Virtual Outlier Synthesisについてまとめました。
個人的な実験でも、かなり精度が良く、OOD検出における実用的な手法だと思います。一方で、モデルの最後から2番目の層の最後のサイズがかなり重要そうで、その設定に悩みました。
Discussion