32 bit float な音源はどれくらい情報を無駄遣いしているのか
PCM 方式
パルス符号変調(Pulse-Code Modulation: PCM)方式は、音声波形などのアナログ信号をデジタル信号に変換するための変調方式のひとつです。 音楽用 CD にも採用されている変調方式であり、比較的身近なデジタル変調方式であるといえます。 PCM 方式では、元のアナログ信号に対して標本化(サンプリング)及び量子化を行い、最終的にデジタル化された数列を得ます。
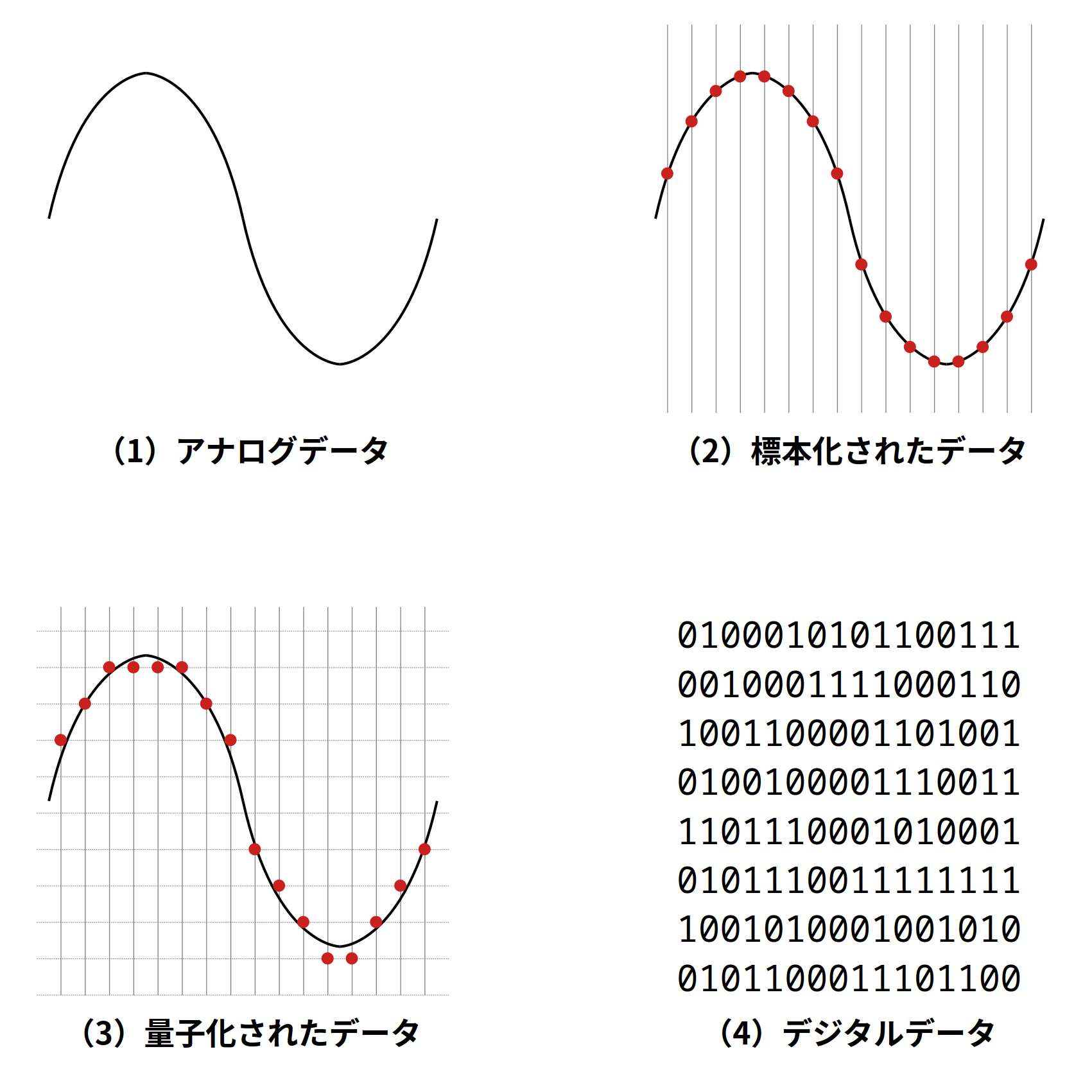
PCM 方式のイメージ
PCM 方式の種類
PCM 方式にはいくつかの種類があります。 特に、量子化の方式によって以下のように分類されます(この他にもさまざまな方式があります)。
-
線形 PCM(Linear PCM: LPCM)
線形に(等間隔に)量子化する方式。 音楽用 CD で用いられている。 -
差分 PCM(Differential PCM: DPCM)
値の差分を用いてデータ量を低らす方式。 ファミコンで用いられていた。 -
浮動小数点数を用いた PCM
量子化の際に浮動小数点数を用いる方式。 今回の主役。
32 bit float な PCM 方式
音楽用 CD などの用途では、サンプリング周波数 44100 Hz、量子化ビット数 16 bit の LPCM を使うことが一般的です。 しかし、より深いオーディオの分野、例えば、DAW の内部処理などでは 32 bit の浮動小数点数(Floating-Point Number)を用いて量子化する PCM が用いられる場合があります。 これによって、より広いダイナミックレンヂ(音の強弱)を記録できるようになり、編集中の意図しないクリッピングノイズ(音割れ)を回避できます。
32 bit float な PCM 方式では、−1.0 から 1.0 の領域を可聴領域と定めています。 32 bit の浮動小数点数では、当然 −1.0 よりも小さい数や 1.0 よりも大きい数を扱えるため、たったこれだけの領域を使うことは情報の無駄遣いに思えて仕方がありません[1]。
どれくらい情報を無駄にしているのか調べてみる
32 bit float な PCM 方式がどれくらい情報を無駄にしているのか、実際に調べてみましょう。 しかし、一体どのようにして調べれば良いのでしょうか。 そもそも、32 bit float では(無効な値を含めて)2 の 32 乗個の値を扱うことできます。 つまり、4294967296 個の値を扱うことができるのです。 このうち、−1.0 から 1.0 までの範囲に入っている値がいくつあるのかを数え上げることで、どれくらいの情報を無駄にしているのかを調べることができます。 これを実現するためには、ある浮動小数点数の次に大きい浮動小数点数を求める必要がありますが、これは nextafter() が実現してくれます。 早速、数え上げプログラムを書いてみましょう。
#include <math.h>
#include <stdio.h>
int
main(void)
{
float f, t;
size_t cnt;
cnt = 0;
for (f = -1.0f; (t = nextafterf(f, 1.0f)) != f; f = t)
cnt++;
printf("-1.0 から +1.0 まで: %zu\n", cnt);
printf("空間使用率: %g\n", cnt / 4294967296.0);
return 0;
}
上のプログラムをコンパイルして実行すると、−1.0 から 1.0 までの範囲に 32 bit の浮動小数点数がいくつあるのかを実際に数え上げます。 そして、その範囲に含まれる浮動小数点数が全体に占める割合を表示します。 なんと、−1.0 から 1.0 までの範囲に浮動小数点数全体の約半分があることがわかります。 つまり、32 bit float な PCM 方式では、浮動小数点数全体で表すことのできる数の半分近い領域を可聴領域に割当てているのです。
$ clang -lm -O2 test.c
$ time ./a.out
-1.0 から +1.0 まで: 2130706432
空間使用率: 0.496094
real 0m13.403s
user 0m13.374s
sys 0m0.001s
おわりに
おわりです。
-
実際のところ、32 bit float な PCM 方式では、−1.0 よりも小さな値や 1.0 よりも大きな値を扱うことがあります。 −1.0 から 1.0 までの領域は可聴領域であるだけで、波形を処理している計算の途中ではこの領域を超えた値になる場合があります。 ↩︎
Discussion