Zenn
🔖

[Unity]六角形ベースの迷路を自動生成する

2021/11/30に公開
Unity
tech

Unityで六角形ベースの迷路の自動生成するメモです。

迷路の自動生成の手順

迷路の自動生成は以下の処理の順序で行います。

  1. 迷路の壁を構成する格子パターンを作成する

  2. 格子パターンと双対となるグラフを作成する

  • グラフからツリーを生成する

  • 生成したツリーを元に、壁の状態を決定する

六角形の座標系

六角形のマップを作成する際、各マスの座標を管理する方法として、2次元の座標で管理する方法と、3次元の座標で管理する方法が考えられます。
六角形のマップにおける座標の管理については、以下のサイトが詳しいです。
https://www.redblobgames.com/grids/hexagons/

3次元で管理する場合、六角形を立方体に見立てて、立方体の座標で各マスの位置を管理します。イメージとしては、以下の画像のように六角形の各頂点への方向を、立方体のX,Y,Z方向と見立てる形になります。

上記の図の場合、選択中の六角形の座標を(0,0,0)とすると、右下が(1,-1, 0)、左下が(0, -1, -1)になります。
六角形の隣接マスの相対座標は以下のようになります。

private Vector3Int[] cubeDirectionVectors = new[]
{
	new Vector3Int(0, 1, -1),
	new Vector3Int(1, 0, -1),
	new Vector3Int(1, -1, 0),
	new Vector3Int(0, -1, 1),
	new Vector3Int(-1, 0, 1),
	new Vector3Int(-1, 1, 0)
};

このX,Y,Zの三方向それぞれに対して、六角形の中心から頂点までの長さのベクトルを定義しておくことで、X,Y,Zの座標とそれぞれのベクトルを掛け合わせることで、2D上での位置に変換することができます。
今回のプログラムの場合、X,Y,Zの軸の方向を以下のように設定しています。

// 六角形の内接円の半径
float radius = 1.0f;

// 六角形の外接円の半径
float circumRadius = radius * 2 / Mathf.Sqrt(3);

// X, Y, Z方向の基準となるベクトルを計算しておく
Vector2 xUnitVector = new Vector2(circumRadius, 0);
Vector2 yUnitVector = new Vector2(-circumRadius * 0.5f, radius);
Vector2 zUnitVector = new Vector2(-circumRadius * 0.5f, -radius);

// x, y, zから2次元上の位置を取得する
public Vector2 GetPosition(Vector3Int cubePosition)
{
	return xUnitVector * cubePosition.x + yUnitVector * cubePosition.y + zUnitVector * cubePosition.z;
}

また、各マスに関するデータを保存する際は、単にZ軸を無視することで、2次元配列に格納することができます。

// 各マスの情報(HexagonData)を格納する二次元配列
private HexagonData[,] hexArray;

private HexagonData GetHex(Vector3Int cubePosition)
{
	return hexArray[cubePosition.x, cubePosition.y];
}

private void SetHex(Vector3Int cubePosition, HexagonData hex)
{
	hexArray[cubePosition.x, cubePosition.y] = hex;
}

なぜZ軸を無視しても問題ないかということですが、これは先にあげた立方体の図をXY平面から見た場合と同じ状態だと考えると分かりやすい気がします。

壁の生成

GameObject.CreatePrimitive(PrimitiveType.Cube)で立方体を生成します。生成した立方体はキャッシュしておき、クローンを生成して迷路の壁に使用します。

private GameObject CreateWall(Transform parent)
{
	// キャッシュが存在する場合、キャッシュを返す
	if (wallCash != null) return Instantiate(wallCash, parent);

	// キャッシュ生成
	var go = GameObject.CreatePrimitive(PrimitiveType.Cube);
	go.name = "Wall";
	var meshRenderer = go.GetComponent<MeshRenderer>();
	meshRenderer.material = wallMat;
	wallCash = go;
	wallCash.SetActive(false);

	return Instantiate(wallCash, parent);
}

生成した壁をハニカム状に並べます。

三角柱の生成

壁を並べていくと壁と壁の間に隙間ができるため、隙間を埋める三角柱を生成します。

private Mesh CreateTriangularPrismMesh()
{
	var mesh = new Mesh();
	var x = wallWidth * 0.5f;
	var y = wallHeight * 0.5f;
	var z = wallWidth / Mathf.Sqrt(3);
	
	// 三角柱の各頂点の位置を計算
	var v0 = new Vector3(0, -y, z);
	var v1 = new Vector3(x, -y, -z * 0.5f);
	var v2 = new Vector3(-x, -y, -z * 0.5f);
	var v3 = new Vector3(0, y, z);
	var v4 = new Vector3(x, y, -z * 0.5f);
	var v5 = new Vector3(-x, y, -z * 0.5f);
	
	// 頂点データを格納
	var vertices = new Vector3[]
	{
		v0, v1, v2, // 底面(0, 1, 2)
		v0, v1, v3, v4, // 側面1(3, 4, 5, 6)
		v1, v2, v4, v5, // 側面2(7, 8, 9, 10)
		v2, v0, v5, v3, // 側面3(11, 12, 13, 14)
		v3, v4, v5 // 上面(15, 16, 17)
	};
	
	// Trisデータを格納
	var triangles = new int[]
	{
		0, 2, 1,	// 底面
		3, 4, 5,	// 側面1
		4, 6, 5,	// 側面1
		7, 8, 9,	// 側面2
		8, 10, 9,	// 側面2
		11, 12, 13,	// 側面3
		12, 14, 13,	// 側面3
		15, 16, 17	// 上面
	};

	mesh.SetVertices(vertices);
	mesh.SetTriangles(triangles, 0);

	// BoundsとNormalを計算
	mesh.RecalculateBounds();
	mesh.RecalculateNormals();

	return mesh;
}

三角柱の頂点は全部で6つなのですが、メッシュを生成する際は面ごとに頂点を定義するようにします。面ごとに頂点を格納しない場合、RecalculateNormalsで法線が正しく計算されません。そのため、全部で18個の頂点をverticesに格納しています。

trianglesは面の表から見て時計回りとなるように頂点を指定していきます。逆順に指定すると、表裏が逆さになってしまい、面が正しく表示されません。

生成したメッシュを元にGameObjectを生成して、キャッシュしておきます。(AddComponentが重いため、毎回生成するよりInstantiateでクローンした方が速いようです)

private GameObject CreateTriangularPrism(Transform parent)
{
	// キャッシュが存在する場合、キャッシュを返す
	if (prismCash != null) return Instantiate(prismCash, parent);

	// 三角柱メッシュを生成
	triangularPrismMesh = CreateTriangularPrismMesh();

	// キャッシュ生成
	var go = new GameObject();
	go.name = "TriangularPrism";
	var meshFilter = go.AddComponent<MeshFilter>();
	meshFilter.mesh = triangularPrismMesh;
	var meshRenderer = go.AddComponent<MeshRenderer>();
	meshRenderer.material = prismMat;
	prismCash = go;
	prismCash.SetActive(false);

	return Instantiate(prismCash, parent);
}

生成した三角柱で壁と壁の隙間を埋めます。

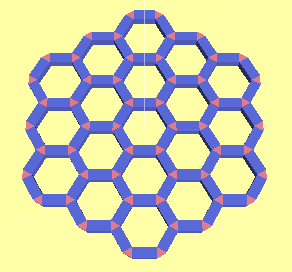
グラフの生成

作成した格子パターンを元に、ノードとエッジからなるグラフを構成します。
六角形がノードと対応し、壁がエッジと対応します。

グラフを生成する際に、各エッジに接続しているノードの情報を保存しておきます。また、ノードにも隣接するノードの情報を保存しておきます。

ツリーの生成

ツリーの作成方法に関しては、以下のサイトの内容が分かりやすいです。

https://www.amusement-creators.info/articles/advent_calendar/2019/11_0/

今回の迷路では、以下のような処理で、ツリーを計算しています。

public static void Calculate(List<Edge> edges, Node[] nodes)
{
	// 全てのノードを異なるグループに振り分ける
	for (var i = 0; i < nodes.Length; i++)
	{
		nodes[i].group = i;
	}

	// 未処理のエッジが無くなるまでループ
	while (edges.Count != 0)
	{
		// エッジをランダムに選択
		int randomIndex = Random.Range(0, edges.Count);
		Edge currentEdge = edges[randomIndex];
		edges.RemoveAt(randomIndex);

		// エッジと繋がっているノードが同じグループに属しているかチェック
		var n0 = nodes[currentEdge.node0];
		var n1 = nodes[currentEdge.node1];
		if (n0.group == n1.group)
		{
			// ノードが同じグループに属している場合
			currentEdge.isConnected = false;
			continue;
		}
		else
		{
			// ノードが別のグループに属している場合
			currentEdge.isConnected = true;
			
			// グループを統合
			if (n0.group < n1.group)
			{
				n1.ChangeGroup(n0.group);
			}
			else
			{
				n0.ChangeGroup(n1.group);
			}
		}
	}
}

ノードとエッジは以下のように定義しています。

// ノードクラス
public class Node
{
	// グループ
	public int group;
	
	// 隣接ノードを格納したリスト
	public List<Node> nodes = new List<Node>();

	// グループを変更する
	public void ChangeGroup(int newGroup)
	{
		var targets = new Queue<Node>();
		targets.Enqueue(this);
		while(targets.Count > 0)
		{
			var targetNode = targets.Dequeue();
			foreach(var node in targetNode.nodes)
			{
				if (node.group == newGroup) continue;
				if (node.group == targetNode.group) 
				{
					targets.Enqueue(node);
				}
			}
			targetNode.group = newGroup;
		}
	}
}

// エッジクラス
public class Edge
{
	// エッジと接続しているノード
	public int node0;
	public int node1;
	// 接続状態
	public bool isConnected;
}

以下のようなツリーが生成されます。

ツリーを元に壁の状態を切り替える

エッジにノードとノードの接続状態が保存された状態になっているため、接続状態になっている場合は、壁を消すようにします。

後記

最終的に作成したコードです。

https://github.com/kuro3vn-gme/MazeHex

Discussion